Квантово-механическая теория строения вещества является фундаментальной научной концепцией современного естествознания, открывающей принципиально новые подходы к изучению мира микрочастиц (элементарных частиц, атомов, молекул и надмолекулярных структур), закономерности которого не могут быть выведены из законов макромира, описываемого классической физикой. Квантовая механика в своей основе сформировалась в 1924-27 годах, однако некоторые предпосылки, послужившие отправной точкой для этой теории, относятся к началу XX века.
Первой предпосылкой возникновения квантово-механической теории следует считать квантовую теорию электромагнитного излучения. В 1900 г. М. Планк, изучая спектр абсолютно черного тела, сформулировал основное положение этой теории следующим образом:
- лучистая энергия испускается и поглощается дискретно в виде целого числа квантов;
- энергия кванта определяется частотой излучения (n) и может быть рассчитана по уравнению:
E = hn,
где h - постоянная Планка (6,625×10-34 Дж×с).
Следующей предпосылкой рассматриваемой теории явилось объяснение закономерностей фотоэффекта - испускания электронов при облучении поверхности металла светом. Экспериментально было установлено, что кинетическая энергия фотоэлектронов зависит от частоты излучения, но не зависит от его интенсивности. От интенсивности излучения зависит только число испускаемых электронов, т.е. сила фототока. В тоже время, согласно электромагнитной теории света энергия фотоэлектронов должна меняться с изменением интенсивности падающего света и не должна зависеть от частоты излучения. А. Эйнштейн (1905 г.) показал, что это противоречие можно устранить, если принять, что свет имеет двойственную природу, являясь одновременно пакетом электромагнитных волн, энергия которых описывается уравнением Планка, и потоком фотонов - частиц с нулевой массой покоя. В этом случае кинетическая энергия фотоэлектрона будет определяться следующим соотношением:
Ек = Еф – А,
где Еф - энергия фотона, А - работа, которую необходимо затратить на удаление электрона из металла (работа выхода). С учетом уравнения Планка:
Ек = hn - А,
то есть энергия фотоэлектронов зависит от частоты излучения и не зависит от его интенсивности.
Третьей предпосылкой квантовой механики является ядерная (планетарная) модель атома, предложенная Э. Резерфордом (1911 г.), в соответствии с которой атом представляет собой систему из положительно заряженного ядра и связанных с ним электронов. Хотя от "планетарного" характера движения электронов вокруг ядра позже пришлось отказаться, ядерная модель атома остается общепризнанной.
В 1913 г. Н. Бор показал, что устойчивость атома водорода и происхождение линий в его спектре могут быть объяснены, если допустить, что разрешенные значения энергии электрона меняются дискретно, а энергетическим уровням отвечают стационарные орбиты определенного радиуса, пребывая на которых электрон не поглощает и не излучает энергию. Теория Бора позволила с высочайшей степенью точности рассчитать атомный спектр водорода, однако распространить ее на другие атомы не удалось. Таким образом к началу двадцатых годов XX века стала очевидной необходимость в новом подходе к описанию объектов микромира.
В основу квантово-механической теории строения атома положена планетарная модель Э. Резерфорда, согласно которой атом состоит из положительно заряженного ядра и электронной оболочки. Основные положения современной квантово-механической теории строения электронной оболочки атома были заложены группой выдающихся физиков-теоретиков: Н. Бор, Луи де Бройль, Э. Шредингер, В. Гейзенберг, М. Планк и др. В основе данной теории лежат два постулата: принцип неопределенности и принцип корпускулярно-волнового дуализма.
Принцип неопределенности (В. Гейзенберг, 1927 г.): невозможно одновременно с высокой точностью определить положение электрона в пространстве (координаты) и его импульс (p = mυ).
Продемонстрируем справедливость этого принципа с помощью следующего мысленного эксперимента. Пусть движущийся электрон освещают потоком фотонов, которые регистрируют с помощью детектора, определяющего координаты и импульс микрочастицы. Положение частицы в пространстве задается координатами (x, y, z ) а ее импульс его проекциями на координатные оси (px, py, pz). Определение импульса будет иметь некоторую погрешность (неопределенность - Dрх, Dрy, Dрz), так как при столкновении с фотоном импульс электрона изменится. Точно также измерение координат будет проведено с некоторой неопределенностью (Dх, Dу, Dz), связанной с дифракцией фотонов на электроне, вследствие чего образ электрона будет размытым.
Предположим, что наблюдатель желает максимально сократить неопределенность положения электрона, уменьшая для этого длину волны фотона (l). Однако это влечет за собой увеличение частоты излучения (n = с/l), а также энергии и импульса фотона:
p =  ,
,
где Ек - кинетическая энергия фотона. В результате столкновение с фотоном существенно изменит импульс электрона, погрешность его определения возрастет, а наблюдаемая траектория электрона станет зигзагообразной.

С другой стороны, уменьшение неопределенности импульса требует уменьшения импульса фотона, для чего необходимо уменьшить его энергию, а, следовательно, увеличить длину волны. Результатом этого будет усиление дифракции и, как следствие, увеличение неопределенности в значениях координат. Экспериментатор увидит вместо точки размытое пятно и не сможет установить, где именно в пределах этого пятна находится электрон.

Таким образом, в микромире инструмент наблюдения взаимодействует с объектом наблюдения, изменяя его характеристики. Рассмотренный мысленный эксперимент показывает, что одновременно уменьшить неопределенность импульса и координат электрона принципиально невозможно.
Математически принцип неопределенности для частицы, движущейся в трехмерном пространстве, выражается тремя неравенствами:
Dx×Dpx ³ h;
Dy×Dpy ³ h;
Dz×Dpz ³ h;
где h =  = 1,05×10-34 Дж×с (постоянная Дирака).
= 1,05×10-34 Дж×с (постоянная Дирака).
Из принципа неопределенности вытекает вывод, необходимый для правильного понимания особенностей микромира: следует отказаться от попыток определить точные значения характеристик микрочастицы (координат, импульса, энергии и т.п.), а попытаться установить их вероятные значения. Модель атома должна быть вероятностной.
При построении вероятностной модели атома пришлось отказаться от понятия "электронная орбита". В квантовой механике это понятие заменено понятием "электронная орбиталь". Электронная орбиталь - это область околоядерного пространства, в которой вероятность нахождения электрона существенно отличается от нуля. Невозможно установить, где именно в пределах орбитали в данный момент находится электрон, но можно оценить вероятность его пребывания в той или иной точке пространства. Таким образом, электрон как бы "размазан" (делокализован) в объеме электронной орбитали, образуя электронное облако.
Важнейшими характеристиками электронной орбитали являются ее граничная поверхность и функция радиального распределения вероятности нахождения электрона. Граничная поверхность определяет форму электронной орбитали. Граничную поверхность строят таким образом, чтобы вероятность нахождения электрона в ограниченном ею пространстве составляла 90 или 95%. Функция радиального распределения показывает вероятность нахождения электрона (W) на разных расстояниях от ядра. На рис. 1 показана граничная поверхность и кривая радиального распределения для основного состояния атома водорода (1s). Граничная поверхность имеет форму сферы, а кривая радиального распределения вероятности проходит через максимум при rmax = 52,9 пм (1 пм = 10-12 м). Заметим, что в квантовой механике rmax характеризуется как наиболее вероятное расстояние между электроном и ядром.

Рис. 1. Граничная поверхность и функция радиального распределения вероятности
1s-орбитали атома водорода.
Принцип корпускулярно-волнового дуализма (Луи де Бройль, 1924 г.) - любому движущемуся материальному объекту можно поставить в соответствие волновой процесс. Уравнение де Бройля легко выводится для электромагнитного излучения, которое одновременно можно рассматривать как волну и как поток элементарных частиц - фотонов.
Если энергия волны определяется уравнением Планка Е = hn, а энергия частицы уравнением Эйнштейна E = mc2, то согласно принципу де Бройля hn = mc2. Частота излучения определяется формулой n = с/l, а следовательно l = h/mс.
Применив данное выражение для любого движущегося материального объекта, получаем:
l = h/mυ = h/p
Из принципа де Бройля вытекает вторая особенность квантовой механики - вероятность нахождения электрона в каждой точке околоядерного пространства должна подчиняться волновым законам.
Волновая функция. Квантовая механика постулирует существование некой специальной функции, с помощью которой могут быть установлены вероятные значения всех характеристик (координат, импульса, энергии и т.д.) электрона или иной микрочастицы. Эта функция обозначается греческой буквой y (пси) и называется волновой функцией или пси-функцией. Волновая функция не имеет простого физического смысла, однако четкий физический смысл имеет ее квадрат. Вероятность нахождения (dW) частицы в бесконечно малом элементе объема (dV), включающем эту точку, пропорциональна величине y2.
dW ~ y2dV
Физический смысл квадрата волновой функции накладывает определенные ограничения на свойства y - функции: она должна быть конечна, непрерывна и однозначна. Действительно, вероятность нахождения электрона в той или иной точке всегда конечна и не может принимать несколько значений. Там, где электрон не может находиться (например, на бесконечно большом расстоянии от ядра), волновая функция должна обращаться в нуль. Волновая функция, удовлетворяющая условию
 = 1,
= 1,
называется нормированной. Условие нормировки означает, что вероятность нахождения электрона в бесконечно большом объеме равна единице, т.е. электрон где-то находится.
Уравнение Шредингера. Квантовая механика использует математический аппарат теории операторов. Оператором называется символ, показывающий, что надо сделать с данной функцией, чтобы превратить ее в некую другую функцию, т.е. оператор - это набор правил, ставящий в соответствие одной функции другую. Например, оператор скорости  выполняет операцию дифференцирования, т.е.
выполняет операцию дифференцирования, т.е.
 f(x) =
f(x) = 
Оператор частного дифференцирования  показывает, что функцию f(x,y...) нужно дважды продифференцировать по x, полагая остальные переменные постоянными.
показывает, что функцию f(x,y...) нужно дважды продифференцировать по x, полагая остальные переменные постоянными.
Квантовая механика утверждает, что каждой физической характеристике b микрочастицы соответствует определенный оператор  (принцип соответствия). Так оператором координаты электрона является сама координата (
(принцип соответствия). Так оператором координаты электрона является сама координата ( = x), импульсу электрона отвечает оператор импульса:
= x), импульсу электрона отвечает оператор импульса:
 = -
= -  , где i =
, где i =  (мнимая единица)
(мнимая единица)
Более сложным является оператор полной энергии (оператор Гамильтона или гамильтониан):
 ,
,
где m - масса электрона, U - его потенциальная энергия, Ñ2 (читается "набла квадрат") - оператор Лапласа (лапласиан):
 ,
,
действие которого предполагает суммирование вторых частных производных, взятых по всем координатам микрочастицы.
Чтобы найти вероятное значение того или иного свойства микрочастицы, нужно подействовать соответствующим оператором на y-функцию, результат умножить на y-функцию и проинтегрировать полученное выражение по всему объему:
b = 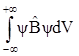
Набор волновых функций, необходимых для определения вероятностных значений свойств частицы, находят, решая основное уравнение квантовой механики (Э. Шредингер, 1926 г.).
 Y = EY,
Y = EY,
где  - оператор полной энергии (оператор Гамильтона, гамильтониан), Е - полная энергия системы.
- оператор полной энергии (оператор Гамильтона, гамильтониан), Е - полная энергия системы.
Кажущаяся простота уравнения исчезает при раскрытии гамильтониана:
 Y + UY = EY
Y + UY = EY





 ,
,

 = 1,05×10-34 Дж×с (постоянная Дирака).
= 1,05×10-34 Дж×с (постоянная Дирака).
 = 1,
= 1, выполняет операцию дифференцирования, т.е.
выполняет операцию дифференцирования, т.е.
 показывает, что функцию f(x,y...) нужно дважды продифференцировать по x, полагая остальные переменные постоянными.
показывает, что функцию f(x,y...) нужно дважды продифференцировать по x, полагая остальные переменные постоянными. (принцип соответствия). Так оператором координаты электрона является сама координата (
(принцип соответствия). Так оператором координаты электрона является сама координата ( = x), импульсу электрона отвечает оператор импульса:
= x), импульсу электрона отвечает оператор импульса: = -
= -  , где i =
, где i =  (мнимая единица)
(мнимая единица) ,
, ,
,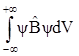
 Y = EY,
Y = EY, Y + UY = EY
Y + UY = EY


