Мет а роботи - вивчення методики цілочислового програмування стосовно оптимізації систем технології термічних печей.
Загальні положення
Для поліпшення експлуатаційних і економічних показників систем термічних печей і технологічного оснащення (допоміжного устаткування, пічних приладів або інших складових системи технологічного устаткування, використовуваних при виконанні ремонтних операцій) може бути застосована методика оптимізації, що ґрунтується на базі цілочислового лінійного програмування.
Цілочислове програмування, будучи одним з модифікованих методів лінійного програмування, дозволяє оптимізувати технічні системи з вельми істотним для технологічного устаткування обмеженням - система, що оптимізується, повинна складатися з цілочислових компонентів. У практиці оптимізації технологічних систем, що складаються з окремих одиниць технологічного устаткування, це обмеження дозволяє відмовитися від некоректного округлення дробової частини змінних, що входять в оптимальний план.
У канонічній формі завдання цілочислового програмування записується таким чином:
A = C1 × X 1 + C 2 × X 2 + ... + C i × X i + ... + C n × X n
P11 × X 1 + P12 × X 2 + ... + P1i × X i + ... + P1n × X n = B1
P21 × X 1 + P22 × X 2 + ... + P2i × X i + ... + P2 n × X n = B2
P j1 × X 1 + P j 2 × X 2 + ... + P ji × X i + ... + P jn × X n = B j
P t1 × X 1 + P t 2 × X 2 + ... + P ti × X i + ... + P tn × X n = B t
X 1 ³ 0, X 2 ³ 0,..., X i ³ 0,..., X n ³ 0
X 1 , X 2 ,..., X i ,..., X n– цілі,
де A – цільова функція, що підлягає оптимізації;
X i – параметр системи, який впливає на цільову функцію;
C i – ціна (числовий коефіцієнт, що описує ступінь впливу змінної на цільову функцію);
B j – обмеження, що накладається на систему зовнішнім середовищем;
P ji –коефіцієнт впливу параметра системи на величину обмеження.
Методика виконання роботи
Завдання цілочислового програмування вирішується в такий послідовності:
- вирішується початкове завдання за звичайним алгоритмом розв’язання задачі лінійного програмування симплекс-методом (наведений у методичних вказівках до попередньої практичної роботи);
- у останню симплекс-таблицю, таку, що містить оптимальний план, додають обмеження на цілочислове значення отриманого рішення (для рядка " j ", що містить найбільшу дробову частину у стовпці вільних членів «В»)
R j1 ×X1 - R j 2 ×X2-...-R ji ×X i -...-R jn ×X n -R jn+1 ×X n+1-.....
-R jn + k×X n + k £ -R j ,
де R – дробова частина числа, що стоїть у рядку "j". R = P - [P] , тобто дорівнює різниці між самим числом P і цілою частиною числа [P] (найбільшого цілого числа, що не перевищує це число);
- коефіцієнти нового обмеження вносяться до рядка "s" останньої симплекс-таблиці, яка в результаті набере вигляду таблиці 1;
Таблиця 1 - Форма симплекс-таблиці, що містить оптимальний план і додаткове обмеження на цілочислове значення
|
N
|
V
|
С
|
B
| C1
| C 2
| …
| Ci
| …
| Cn
| Cn+k
|
| X1
| X 2
| …
| Xi
| …
| Xn
| Xn+k
|
| 1
| Xi
| C1
| B1
| P1,1
| P1,2
| …
| P1,i
| …
| P1,n
| P1,n +k
|
| 2
| Xi
| C 2
| B 2
| P2,1
| P2,2
| …
| P2,i
| …
| P2,n
| P2,n + k
|
| j
| Xi
| C j
| B j
| Pj,1
| Pj,2
| …
| Pj,i
| …
| Pj,n
| Pj,n + k
|
| t
| Xi
| C t
| B t
| Pt,1
| Pt,2
| …
| Pt,i
| …
| Pt,n
| Pt,n + k
|
| s
| --
| --
| - R j
| - R j,1
| - R j,2
| …
| - R j,i
| …
| - R j,n
| - R j,n + k
|
| t+1
| --
| --
| A'
| C1'
| C2 '
| …
| Ci '
| …
| Cn '
| Cn + k '
|
- введений рядок "s" вибирається як розв’язуючий;
- розв’язуючий стовпець вибирається за найменшим за абсолютною величиною відношенням елементів «t+1» рядка до невід’ємних елементів розв’язуючого рядка. Йому привласнюється номер «q»;
- визначається розв’язуючий елемент R sq , який знаходиться на перетині розв’язуючого стовпця і рядка;
- записуються елементи s-строки, що стоять у стовпці «V» і «С» (вибираються з верхнього рядка розв’язуючого стовпця);
- елементи s-рядка діляться на розв’язуючий елемент, тобто обчислюються
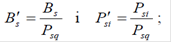
- решта всіх елементів симплекс-таблиц (окрім еле-
ментів стовбців «B» і «С») обчислюються за формулою:
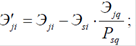
- за наявності у стовпці вільних членів «B» елементів, що містять дробову частину, вводиться ще одне додаткове обмеження, і процес повторюють до отримання цілочисло- вого рішення.
Приклад виконання роботи
Знайти: maxY = X 1 + 2 × X 2 (min Y = - X 1 - 2 × X 2 )
за умов:
X 1 - 2 × X 2 £ 2
- 2 × X 1 + X 2 £ 2
X 1 + X 2 £ 3
X 1 ³ 0 X 2 ³ 0 ; X 1 , X 2– цілі.
 Не зважаючи на вимогу цілочислового рішення X 1 і X2, завдання вирішується симплекс-методом до отримання оптимального плану.
Не зважаючи на вимогу цілочислового рішення X 1 і X2, завдання вирішується симплекс-методом до отримання оптимального плану.
max( submatrix( A , 6 , 6 , 5 , 9) ) = 2
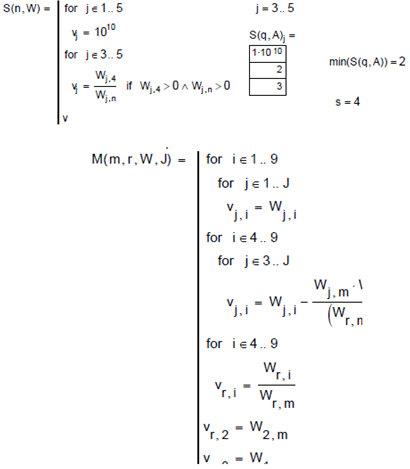
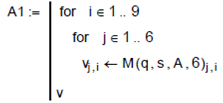
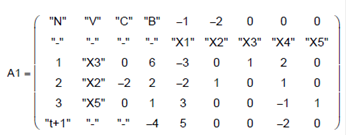
max (submatrix (A1 , 6 , 6 , 5 , 9)) = 5 q = 5

Матриця А2 містить оптимальний план (у рядку "t+1" немає додатних елементів).
У стовбці вільних членів «В» не всі елементи цілі.
Оскільки у другому рядку цього стовпця міститься найбільша дробова частина, то для неї складається додаткове обмеження:

Складене додаткове обмеження включається рядком з номером "s" в останню симплекс-таблицю, таку, що міс- тить оптимальний план.
Ao := submatrix (A2 , 1 , 5 , 1 , 9)
Ac := stack (Ao , As )
Ao := submatrix (A2 , 6 , 6 , 1 , 9) Ac := stack (Ac , Ao)
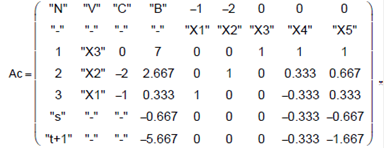
«s» - рядок вибирається як розв’язуючий.
Знаходимо відношення елементів рядка "t+1" до відповідних невід’ємних елементів рядка "s" і знаходимо найменше за абсолютною величиною.

Беремо стовпець X4, що містить мінімальне відношення, як розв’язуючий, а елемент, який знаходиться на перетині розв’язуючого рядка і стовпця, як розв’язуючий елемент.
Переписуються елементи стовбців «V» і «С», перера- ховуються елементи "s"-рядка і потім решта всіх елементів симплекс-таблиці.

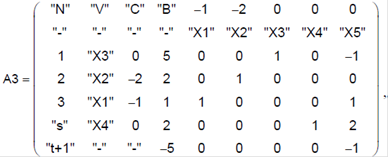 У стовпці «В» всі елементи цілі. Отриманий оптимальний цілочисловий план X 1 = 1, X 2 = 2, max Y = 5 (коефіцієнти X 3 = 5 , X 4 = 2 входять в отримане рішення, проте в оптимальний план не включаються, оскільки мають ціни C3 = C4 = 0 і не впливають на величину цільової функції).
У стовпці «В» всі елементи цілі. Отриманий оптимальний цілочисловий план X 1 = 1, X 2 = 2, max Y = 5 (коефіцієнти X 3 = 5 , X 4 = 2 входять в отримане рішення, проте в оптимальний план не включаються, оскільки мають ціни C3 = C4 = 0 і не впливають на величину цільової функції).
Вимоги до змісту звіту
Звіт повинен містити:
1 Найменування і мету роботи.
2 Результати проміжних розрахунків – ітерацій.
3 Висновки про результати оптимізації.
Варіанти завдань
Як завдання для цілочислового програмування узяти результати оптимізації плану використання чотирьох типів печей для устаткування термічного цеху, отримані в прак- тичній роботі «Оптимізація оснащення термічного цеху методом лінійного програмування».





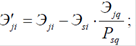
 Не зважаючи на вимогу цілочислового рішення X 1 і X2, завдання вирішується симплекс-методом до отримання оптимального плану.
Не зважаючи на вимогу цілочислового рішення X 1 і X2, завдання вирішується симплекс-методом до отримання оптимального плану.
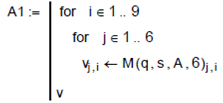






 У стовпці «В» всі елементи цілі. Отриманий оптимальний цілочисловий план X 1 = 1, X 2 = 2, max Y = 5 (коефіцієнти X 3 = 5 , X 4 = 2 входять в отримане рішення, проте в оптимальний план не включаються, оскільки мають ціни C3 = C4 = 0 і не впливають на величину цільової функції).
У стовпці «В» всі елементи цілі. Отриманий оптимальний цілочисловий план X 1 = 1, X 2 = 2, max Y = 5 (коефіцієнти X 3 = 5 , X 4 = 2 входять в отримане рішення, проте в оптимальний план не включаються, оскільки мають ціни C3 = C4 = 0 і не впливають на величину цільової функції).


