Мета роботи - вивчення методики перевірки згоди дослідного розподілу з теоретичним при контролі твердості.
Загальні положення
Після остаточної термічної обробки деталей згідно із технічними умовами креслення контролюється твердість серцевини, а при проведенні хіміко-термічної обробки, твердість і глибина поверхневого шару. При такому контролі знову виготовлених деталей, як правило, використовують нормальний закон розподілу вимірюваних величин.
У ряді випадків це виправдано, оскільки встановлено, що в машинобудуванні більшість випадкових процесів підкоряються нормальному закону розподілу. В той самий час є процеси, які не підкоряються цьому закону, і застосування до них оцінок, відповідних нормальному закону розподілу, призводить до істотних похибок. (Навіть середнє значення при розподілах, що не підкоряються нормальному закону, може обчислюватися за формулами, відмінними від традиційної формули, наприклад, при розподілі Вейсбула:
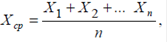
Тому перед визначенням оцінок випадкових величин, використовуваних для різних теоретико-вірогідних розрахунків, доцільно заздалегідь встановити закон розподілу контрольованої випадкової величини.
Процедура встановлення закону розподілу випадкової величини полягає в отриманні впорядкованого ряду результатів спостережень цієї величини X1 £ X2 X3 ... Xn, побудові за ним функції накопичених частковостей і порівнянні цієї функції із заданою теоретичною функцією. Спостереження випадкової величини Х повинні проводитися в практично однакових умовах, досліджувана сукупність повинна бути однорідною. Порушення вимог однорідності може призвести до помилкових висновків.
Число спостережень випадкової величини для перевірки узгодження дослідного і теоретичного розподілів повинне бути більше 50, якщо використовується v-критерий, більше 100 - якщо використовується критерій Колмогорова (або будь-який інший критерій). Для вимірювання необхідно застосовувати засоби вимірювання з ціною поділки, що не перевищує 1/5 передбачуваної величини середнього квадратичного відхилення досліджуваного розподілу.
Методика виконання роботи
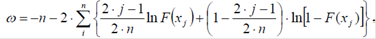 Обчислюється значення величини v за формулою:
Обчислюється значення величини v за формулою:
де n - число спостережень (n ³ 50); Xj - результат спостережень, j - номер X у варіаційному ряду, отримуваний при впорядкуванні результатів в порядку їх зростання, тобто X1 £ X2 £ K £ Xn (j =1,2,...,n); F(Xj) - значення
функції теоретичного розподілу при значенні аргументу, що дорівнює Xj. Визначається за статистичними таблицями функцій розподілу, наведеними у відповідних довідниках (для нормального закону розподіли наведені в таблиці 1). При обчисленнях за допомогою пакета MATHCAD, як правило, застосовується вбудована функція pnorm.
Таблиця 1 - Значення функції нормального розподілу.
| t
| F(t)
| t
| F(t)
| t
| F(t)
| T
| F(t)
|
| 0.00
| 0.50000
| 1.00
| 0.84134
| 2.00
| 0.97725
| 3.00
| 0.99865
|
| 0.05
| 0.51994
| 1.05
| 0.85314
| 2.05
| 0.97725
| 3.05
| 0.99886
|
| 0.10
| 0.53983
| 1.10
| 0.86433
| 2.10
| 0.98214
| 3.10
| 0.99903
|
| 0.15
| 0.55962
| 1.15
| 0.87493
| 2.15
| 0.98442
| 3.15
| 0.99918
|
| 0.20
| 0.57926
| 1.20
| 0.88493
| 2.20
| 0.98610
| 3.20
| 0.99931
|
| 0.25
| 0.59871
| 1.25
| 0.89435
| 2.25
| 0.98778
| 3.25
| 0.99942
|
| 0.30
| 0.61791
| 1.30
| 0.90320
| 2.30
| 0.98928
| 3.30
| 0.99952
|
| 0.35
| 0.63683
| 1.35
| 0.91149
| 2.35
| 0.99061
| 3.35
| 0.99960
|
| 0.40
| 0.65542
| 1.40
| 0.91924
| 2.40
| 0.99180
| 3.40
| 0.99966
|
| 0.45
| 0.67364
| 1.45
| 0.92647
| 2.45
| 0.99286
| 3.45
| 0.99972
|
| 0.50
| 0.69146
| 1.50
| 0.93319
| 2.50
| 0.99379
| 3.50
| 0.99977
|
| 0.55
| 0.70884
| 1.55
| 0.93943
| 2.55
| 0.99461
| 3.55
| 0.99981
|
| 0.60
| 0.72575
| 1.60
| 0.94520
| 2.60
| 0.99534
| 3.60
| 0.99984
|
| 0.65
| 0.74215
| 1.65
| 0.95053
| 2.65
| 0.99598
| 3.65
| 0.99987
|
| 0.70
| 0.75804
| 1.70
| 0.95543
| 2.70
| 0.99653
| 3.70
| 0.99989
|
| 0.75
| 0.77337
| 1.75
| 0.95994
| 2.75
| 0.99702
| 3.75
| 0.99991
|
| 0.80
| 0.78814
| 1.80
| 0.96407
| 2.80
| 0.99744
| 3.80
| 0.99993
|
| 0.85
| 0.80234
| 1.85
| 0.96784
| 2.85
| 0.99781
| 3.85
| 0.99994
|
| 0.90
| 0.81594
| 1.90
| 0.97128
| 2.90
| 0.99813
| 3.90
| 0.99995
|
| 0.95
| 0.82894
| 1.95
| 0.97441
| 2.95
| 0.99841
| 3.95
| 0.99996
|
|
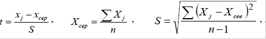 де Xсер, S - відповідно середньоарифметичне і середньоквадратичне за n спостереженнями. Якщо t<0, то табличне значення потрібно відняти від 1 де Xсер, S - відповідно середньоарифметичне і середньоквадратичне за n спостереженнями. Якщо t<0, то табличне значення потрібно відняти від 1
|
Задається рівень значущості B. При контролі твердості рекомендується вибирати значення B, що дорівнює 0.05.
Якщо b ³ (1 - B), то гіпотезу про згоду емпіричного і теоретичного розподілу відкидають, якщо b < (1 - B), то
гіпотезу приймають
У таблиці 2 подані значення функції b, відповідне об- численому значенню v (функція b є функцією розподілу величини v). При v більше 2.45 беруть b = 1.
Таблиця2. Функція розподілу величини v
| v
| b
| v
| b
| v
| b
| v
| b
| v
| b
|
| 0.00
| 0.000
| 0.50
| 0.253
| 1.00
| 0.643
| 1.50
| 0.824
| 2.00
| 0.908
|
| 0.05
| 0.000
| 0.55
| 0.294
| 1.05
| 0.663
| 1.55
| 0.833
| 2.05
| 0.913
|
| 0.10
| 0.000
| 0.60
| 0.352
| 1.10
| 0.691
| 1.60
| 0.846
| 2.10
| 0.919
|
| 0.15
| 0.001
| 0.65
| 0.389
| 1.15
| 0.709
| 1.65
| 0.854
| 2.15
| 0.923
|
| 0.20
| 0.010
| 0.70
| 0.441
| 1.20
| 0.732
| 1.70
| 0.865
| 2.20
| 0.929
|
| 0.25
| 0.025
| 0.75
| 0.474
| 1.25
| 0.747
| 1.75
| 0.872
| 2.25
| 0.932
|
| 0.30
| 0.062
| 0.80
| 0.519
| 1.30
| 0.768
| 1.80
| 0.881
| 2.30
| 0.937
|
| 0.35
| 0.095
| 0.85
| 0.547
| 1.35
| 0.780
| 1.85
| 0.887
| 2.35
| 0.940
|
| 0.40
| 0.151
| 0.90
| 0.586
| 1.40
| 0.798
| 1.90
| 0.896
| 2.40
| 0.944
|
| 0.45
| 0.192
| 0.95
| 0.610
| 1.45
| 0.809
| 1.95
| 0.901
| 2.45
| 0.947
|
Виконання вимірювань
Твердість в більшості випадків випробовується при статичному характері втискування індентора у вигляді кульки, конуса або піраміди в тіло досліджуваного об'єкта або дряпанням поверхневого шару пірамідою з твердого матеріалу.
У даний час існує понад 30 методів вимірювання твердості, але найбільш широке застосування знайшли методи Бринеля, Роквела і Віккерса.
Твердість за Роквелом вимірюють на приладах «ТК» шляхом втискування в досліджуваний об'єкт діамантового
конусу з кутом при вершині 120° або сталевої кульки діаметром 1,58 мм (рисунок 1). Твердість записують так: HRC 60, HRB 98, HRA 70.
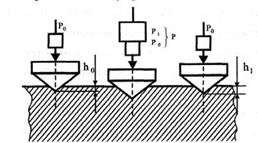
Рисунок 1 - Втискування конуса
Приклад виконання роботи
Початкові дані, отримані при вимірюванні твердості сталі 4Х5МФ1С, що зазнала термообробки (гартування 10200, відпуск 5800), наведені в таблиці 4, а варіаційний ряд, складений у результаті їх впорядкування, - у таблиці 5.
Встановити, чи підкоряються наведені результати вимірювання твердості нормальному закону розподілу.
Таблиця 4 –Резул ьтати вимірювання твердості
| №
| HRC
| №
| HRC
| №
| HRC
| №
| HRC
| №
| HRC
|
| 1
| 44
| 2
| 44
| 3
| 43
| 4
| 45
| 5
| 46
|
| 6
| 46
| 7
| 44
| 8
| 48
| 9
| 48
| 10
| 47
|
| 11
| 48
| 12
| 46
| 13
| 47
| 14
| 44
| 15
| 46
|
| 16
| 46
| 17
| 44
| 18
| 45
| 19
| 47
| 20
| 47
|
| 21
| 48
| 22
| 49
| 23
| 48
| 24
| 45
| 25
| 48
|
| 26
| 47
| 27
| 44
| 28
| 45
| 29
| 47
| 30
| 47
|
| 31
| 48
| 32
| 48
| 33
| 44
| 34
| 45
| 35
| 46
|
| 36
| 48
| 37
| 46
| 38
| 47
| 39
| 47
| 40
| 47
|
| 41
| 44
| 42
| 44
| 43
| 48
| 44
| 48
| 45
| 44
|
| 46
| 45
| 47
| 47
| 48
| 45
| 49
| 47
| 50
| 48
|
Таблиця 5 – Варіаційний ряд
| J
| Xj
| j
| Xj
| j
| Xj
| j
| Xj
| j
| Xj
| j
| Xj
| j
| Xj
| j
| Xj
|
| 1
| 43
| 2
| 44
| 3
| 44
| 4
| 44
| 5
| 44
| 6
| 44
| 7
| 44
| 8
| 44
|
| 9
| 44
| 10
| 44
| 11
| 44
| 12
| 45
| 13
| 45
| 14
| 45
| 15
| 45
| 16
| 45
|
| 17
| 45
| 18
| 45
| 19
| 46
| 20
| 46
| 21
| 46
| 22
| 46
| 23
| 46
| 24
| 46
|
| 25
| 46
| 26
| 47
| 27
| 47
| 28
| 47
| 29
| 47
| 30
| 47
| 31
| 47
| 32
| 47
|
| 33
| 47
| 34
| 47
| 35
| 47
| 36
| 47
| 37
| 47
| 38
| 48
| 39
| 48
| 40
| 48
|
| 41
| 48
| 42
| 48
| 43
| 48
| 44
| 48
| 45
| 48
| 46
| 48
| 47
| 48
| 48
| 48
|
| 49
| 48
| 50
| 49
|
|
|
|
|
|
|
|
|
|
|
|
|

Оцінки параметрів нормального розподілу, обчислені за початковими даними, дорівнюють відповідно Xсер = 46,18, D = 1,587. Беремо ці оцінки як значення параметрів нормального розподілу.
Результати подальших обчислень наведені в таблиці 6 (з метою ілюстрації обчислювального процесу наводяться результати проміжних розрахунків, тільки для перших п'я- ти значень варіаційного ряду).
 Та блиця 6 – Обчислення пр оміжних значень
Та блиця 6 – Обчислення пр оміжних значень
|
j
| 2 j - 1
2n
|
F(xj)
|
Ln(3)
| (2)´(4)
|
1-(2)
|
1-(3)
|
Ln(7)
| (6) ´(8)
| (5) + (9)
|
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
|
| 1
| 0,01
| 0,023
| -3,793
| -0,038
| 0,99
| 0,977
| -0,023
| -0,023
| -0,06
|
| 2
| 0,03
| 0,085
| -2,468
| -0,074
| 0,97
| 0,915
| -0,089
| -0,086
| -0,16
|
| 3
| 0,05
| 0,085
| -2,468
| -0,123
| 0,95
| 0,915
| -0,089
| -0,084
| -0,208
|
| 4
| 0,07
| 0,085
| -2,468
| -0,173
| 0,93
| 0,915
| -0,089
| -0,082
| -0,255
|
| 5
| 0,09
| 0,085
| -2,468
| -0,222
| 0,91
| 0,915
| -0,089
| -0,081
| -0,303
|
Сума всіх п'ятидесяти значень, які повинні бути у графі 10, дорівнює –25,952. Тоді результат обчислень
v = -50 – 2 х (–25,952) = 1,905
і, згідно з таблицею 1.2, йому відповідає величина b = 0.896.
Задаючи B = 0.05, маємо b = 0.896 < (1 - 0.05).
Отже, гіпотеза про те, що вибірка належить нормально розподіленій генеральній сукупності, не може бути знехтувана.
Вимоги до змісту звіту
Звіт повинен містити:
1 Найменування і мету роботи.
2 Результати проміжних розрахунків.
3 Висновки.
Варіанти завдань
Варіанти завдань узяти з таблиці 7 (для підваріанта A -результати з 1-го по 50-те вимірювання, B - результати з 11-го по 60-те вимірювання, C - результати з 21-го по 70-те вимірювання D - результати з 31-го по 80-те вимірювання, E - результати з 41-го по 90-те вимірювання, F - результати з 51-го по 100-те вимірювання ).
Таблиця 7 – Результати вимірювання твердості сталі після остаточної термічної обробки (за Роквелом HRC)
| Варіант 1 (сталь 3Х2В8Ф, гарт.1120-11600, відп.660-6800)
|
|
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
|
| 1-10
| 40
| 41
| 42
| 43
| 45
| 40
| 42
| 40
| 44
| 45
|
| 11-20
| 41
| 42
| 40
| 42
| 45
| 43
| 40
| 42
| 41
| 45
|
| 21-30
| 41
| 42
| 43
| 44
| 44
| 45
| 40
| 42
| 40
| 41
|
| 31-40
| 41
| 40
| 45
| 42
| 43
| 43
| 45
| 41
| 40
| 41
|
| 41-50
| 40
| 42
| 45
| 41
| 41
| 41
| 42
| 45
| 44
| 43
|
| 51-60
| 41
| 44
| 40
| 41
| 41
| 44
| 43
| 41
| 41
| 42
|
| 61-70
| 45
| 45
| 45
| 40
| 40
| 41
| 43
| 42
| 40
| 41
|
| 71-80
| 42
| 41
| 44
| 41
| 42
| 42
| 42
| 40
| 42
| 43
|
| 81-90
| 43
| 40
| 44
| 42
| 45
| 41
| 41
| 45
| 44
| 44
|
| 91-100
| 41
| 42
| 44
| 45
| 43
| 45
| 41
| 44
| 45
| 45
|
Продовження табл.1
|
Варіант 2 (сталь 5ХНМ, гарт.8500, відп. 460-5200)
|
| 1-10
| 37
| 38
| 42
| 37
| 37
| 38
| 37
| 37
| 38
| 40
|
| 11-20
| 42
| 41
| 40
| 38
| 38
| 42
| 38
| 41
| 37
| 40
|
| 21-30
| 39
| 41
| 38
| 42
| 39
| 42
| 40
| 42
| 38
| 42
|
| 31-40
| 40
| 40
| 41
| 40
| 40
| 41
| 39
| 42
| 39
| 38
|
| 41-50
| 41
| 42
| 39
| 39
| 41
| 40
| 40
| 41
| 40
| 42
|
| 51-60
| 38
| 42
| 37
| 38
| 42
| 39
| 41
| 40
| 40
| 38
|
| 61-70
| 37
| 42
| 38
| 40
| 37
| 38
| 42
| 39
| 41
| 37
|
| 71-80
| 42
| 41
| 37
| 41
| 38
| 37
| 41
| 40
| 42
| 37
|
| 81-90
| 39
| 40
| 42
| 42
| 39
| 42
| 40
| 39
| 38
| 42
|
| 91-100
| 37
| 38
| 40
| 41
| 40
| 41
| 37
| 38
| 38
| 41
|
|
Варіант 3 (сталь P9М4К8,гарт.12200,відп.3 крат. 5400)
|
| 1-10
| 69
| 67
| 69
| 67
| 66
| 67
| 69
| 69
| 68
| 67
|
| 11-20
| 68
| 68
| 69
| 68
| 69
| 67
| 68
| 69
| 68
| 66
|
| 21-30
| 67
| 68
| 68
| 67
| 69
| 66
| 69
| 67
| 69
| 68
|
| 31-40
| 66
| 69
| 68
| 68
| 68
| 67
| 67
| 68
| 67
| 69
|
| 41-50
| 69
| 66
| 67
| 69
| 68
| 68
| 66
| 68
| 68
| 69
|
|
Варіант 1 (сталь 3Х2В8Ф, гарт.1120-11600,відп.660-6800)
|
|
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
|
| 51-60
| 67
| 67
| 69
| 69
| 67
| 69
| 69
| 69
| 69
| 68
|
| 61-70
| 69
| 68
| 67
| 69
| 67
| 68
| 67
| 66
| 67
| 69
|
| 71-80
| 68
| 69
| 66
| 66
| 69
| 69
| 68
| 67
| 69
| 67
|
| 81-90
| 67
| 69
| 67
| 67
| 67
| 69
| 69
| 68
| 69
| 68
|
| 91-100
| 69
| 68
| 68
| 69
| 69
| 69
| 67
| 69
| 69
| 68
|
| | | | | | | | | | | | | | | | | | | |
Продовження табл. 1
| Варіант 4 (сталь 30ХГСА,гарт.8800, відп.2300)
|
| 1-10
| 43
| 44
| 45
| 44
| 45
| 51
| 51
| 43
| 45
| 45
|
| 11-20
| 44
| 43
| 46
| 43
| 44
| 50
| 50
| 49
| 43
| 43
|
| 21-30
| 45
| 51
| 47
| 50
| 43
| 49
| 49
| 48
| 43
| 44
|
| 31-40
| 46
| 50
| 48
| 51
| 44
| 48
| 43
| 46
| 43
| 43
|
| 41-50
| 47
| 49
| 49
| 51
| 45
| 47
| 44
| 43
| 44
| 50
|
| 51-60
| 48
| 48
| 50
| 50
| 46
| 46
| 45
| 51
| 45
| 50
|
| 61-70
| 49
| 47
| 51
| 49
| 47
| 45
| 46
| 43
| 46
| 51
|
| 71-80
| 50
| 46
| 43
| 48
| 48
| 44
| 47
| 51
| 47
| 51
|
| 81-90
| 51
| 45
| 44
| 47
| 49
| 43
| 48
| 50
| 48
| 51
|
| 91-100
| 43
| 44
| 45
| 46
| 50
| 51
| 49
| 50
| 49
| 50
|
| Варіант 5 (сталь Х12М,гарт.9700,відп.3200)
|
| 1-10
| 58
| 59
| 60
| 59
| 60
| 61
| 58
| 59
| 58
| 59
|
| 11-20
| 59
| 59
| 61
| 61
| 61
| 60
| 59
| 59
| 58
| 58
|
| 21-30
| 60
| 58
| 58
| 61
| 61
| 61
| 59
| 58
| 59
| 59
|
| 31-40
| 61
| 58
| 59
| 60
| 61
| 59
| 58
| 61
| 60
| 61
|
| 41-50
| 58
| 61
| 60
| 60
| 61
| 58
| 60
| 60
| 61
| 60
|
| 51-60
| 59
| 60
| 62
| 61
| 60
| 61
| 61
| 61
| 58
| 58
|
| 61-70
| 60
| 59
| 61
| 62
| 60
| 60
| 61
| 60
| 59
| 60
|
| 71-80
| 61
| 58
| 60
| 58
| 59
| 59
| 61
| 59
| 60
| 60
|
| 81-90
| 58
| 61
| 60
| 59
| 59
| 58
| 60
| 58
| 61
| 59
|
| 91-100
| 59
| 60
| 58
| 59
| 58
| 59
| 58
| 58
| 58
| 58
|
СПИСОК ЛІТЕРАТУРИ
1.
2. Алексеев А.Н., Волков Н.И.Компьютер в учебном процессе высшей школы: Учебное пособие. - Сумы: Довілля, 2002. - 380 с.
3.
.
4. Одиноков В.И. Математическое моделирование сложных технологических процессов. – М.: Наука , 2008. -
175 с.
5. Рубцов В. П., Погребисский М. Я. Моделирование в технике: Учебное пособие. - М.: Геодезия, 2008. - 103 с.
6. Максимов В. П., Егоров И. В., Карасев В. А. Изме- рение, обработка и анализ быстропеременных процессов в машинах. - М.: Машиностроение, 1987. - 207 с.
7. Рубановский В.Н., Султанов И.А., Ханукаев Ю.И. Задачи математического моделирования механических систем в машиностроении. - М.: ВЦ АН СССР, 1989. - 76 с.
8. Остроменский П.И. Математическое моделирование в машиностроении. - Новосибирск: НЭТИ , 1990. - 83 с.
9. Макашов Э.М., Шаронова И.М. Моделирование ин-
женерных задач на ЭЦВМ: Учебное пособие. - М.: МАИ,
1984. - 68 с.





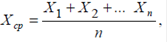
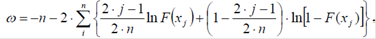 Обчислюється значення величини v за формулою:
Обчислюється значення величини v за формулою: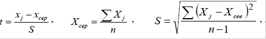 де Xсер, S - відповідно середньоарифметичне і середньоквадратичне за n спостереженнями. Якщо t<0, то табличне значення потрібно відняти від 1
де Xсер, S - відповідно середньоарифметичне і середньоквадратичне за n спостереженнями. Якщо t<0, то табличне значення потрібно відняти від 1

 Та блиця 6 – Обчислення пр оміжних значень
Та блиця 6 – Обчислення пр оміжних значень

