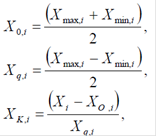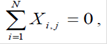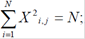Мета роботи - вивчити метод найменших квадратів і можливість його застосування для визначення ступеня надійності сталі залежно від температури відпуску
Загальні положення
Через різні причини у процесі експлуатації деталі ма- шин можуть піддаватися короткочасному впливу навантажень (ударам). Тому для визначення здатності деталі до крихкого руйнування важливо установити, чи існує математична залежність між температурою відпуску і значенням ударної в'язкості. Наявність такої залежності дає мож- ливість з високим ступенем точності прогнозувати надій- ність деталі в умовах експлуатації.
Установити математичну залежність між значенням температури відпуску і значенням ударної в'язкості дозво- ляє регресійний аналіз. Він називається парним, якщо визначається Y = f (X), тобто залежність одного з показників обробки деталі (Y- температура відпуску) – або експлуатаційної характеристики (X- ударна в'язкість).За видом залежності Y = f (X) парний регресійний аналіз може бути лінійним, гіперболічним, ступеневим і т.д. Сутність лінійного парного регресійного аналізу полягає у визначенні параметрів емпіричної лінійної залежності
Y( X) = a + bX,
що описує зв'язок між деяким числом N пар вимірюваних значень експлуатаційного показника (вихідними парамет- рами Yi) і умовами експлуатації, оцінюваними вхідними параметрами (Xi). При цьому повинна забезпечуватися найменша середньоквадратична похибка від заміни експериментально отриманих значень їхньою математичною моделлю.
Графічно задачу парного лінійного регресійного аналі- зу можна представити в такий спосіб - у безлічі точок XiYi площини XY (рисунок 1) потрібно провести пряму так, щоб величина усіх відхилень від прямої відповідала умові
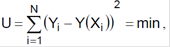
де Yi - ордината точки i, у якої абсциса дорівнює Хi
Y(Xi) - ордината прямої, описуваної залежності Y (X) = a + bX при абсцисі Xi.
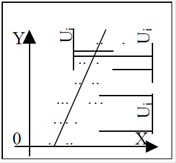
Рисунок 1 - Залежність Y = a + bX
Відомо, що для знаходження мінімуму функції необхідно її частинні похідні прирівняти до нуля, тобто
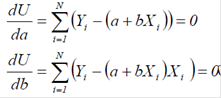
N
і, отже, можна скласти систему лінійних рівнянь для визначення невідомих коефіцієнтів a і b:
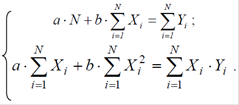
Розв׳язання системи дає коефіцієнти a і b у рівнянні прямої Y = a + bX :
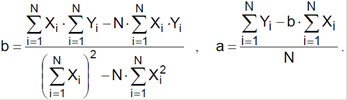
Точність регресійного аналізу оцінюється величиною середньоквадратичного відхилення, що повинне бути мінімальним
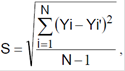
де Yi`- значення функції, розраховані за отриманими формулами при підстановці коефіцієнтів a, b і аргумента Xi;
Yi - значення вихідного параметра.
Нелінійна парна регресія може бути зведена до лінійної за допомогою лінеаризуючих перетворень (таблиця 1).
Згідно з таблицею 1 випливає, що якщо, наприклад, потрібно побудувати експонентну залежність типу a ' + eb'X, то можна скористатися виразами, одержаними при розв’язанні системи рівнянь стосовно a і b, однак у них замість Yi варто підставляти значення Ln(Yi); обчислені значення а і b повинні бути перераховані за формулами a' = e a , b` = b.
Таблиця 1 – Лінеаризуючі перетворення
| Лінеаризована функція
| Значення X,Y , що підставляють
у формули для обчислення a і b
|
Формули перерахування a= b=
|
|
Назва
|
Формула
|
|
Гіперболічна
| '
a' + b
X
|
1
X
|
Y
|
A
|
b
|
| Ступенева
| a × Xb'
| Ln(X)
| Ln(Y)
| ea
| b
|
| Показникові
| a × b X
| X
| Lg(Y)
| 10a
| 10b
|
| Експонентна
| a' × eb'×X
| X
| Ln(Y)
| ea
| b
|
|
Логарифмічна
| a' + b' × Lg(X)
a' + b' × Ln(X)
|
Lg(X) Ln(X)
|
Y Y
|
a
A
|
b b
|
З таблиці 1 видно також, що регресійний аналіз дозво- ляє представити шукану математичну залежність у вигляді лінійної, гіперболічної, показової, статичної, логарифмічної або якоїсь іншої залежності. Очевидно, що вибрати потрібно таку залежність, що найбільше точно визначає стійкість сталі до крихкого руйнування (залежність ударної в'язкості від температури відпуску сталі), тобто, коли регресійний аналіз проведений найбільше точно.
Ефективним засобом регресійного аналізу є поліноміальна регресія, точність якої може бути як завгодно велика.
Полягає вона в апроксимації досліджуваних даних поліномом вигляду
Y(X) = A(0) + A 1X + A 2 X 2 + K + A m Xm ,
причому чим більше показник степеня "m", тим вище може бути забезпечена точність апроксимації.
Коефіцієнти полінома знаходяться із системи рівнянь

Частковим випадком поліномної регресії є параболічна, яка забезпечує апроксимацію параболічною функцією виду
Y(X) = A 0 + A1 * X + A 2 * X2 ,
коефіцієнти A o , A1, A 2 знаходять із системи рівнянь
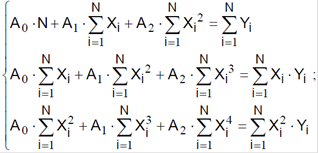
Розв’язати цю систему лінійних рівнянь можна будь-яким відомим методом, наприклад методом Гауса.
Методика виконання роботи
Лінійна регресія:
- визначаються пари значень KCUi, ti і розраховуються суми å KCU i , å t i, å KCU2 i , å KCU i × t i ;
- складається і вирішується система вихідних рівнянь для знаходження коефіцієнтів a і b за формулами
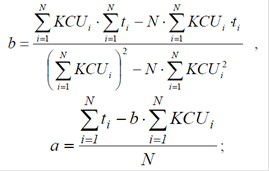
- оцінюється точність апроксимації за середньоквадратичним відхиленням
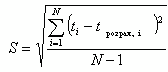
Нелінійна регресія:
- визначаються пари значень Xi, Yi;
- вибирається вид функціональної залежності, за якою
буде виконуватися апроксимація (у завданні до виконання
практичної роботи потрібно виконати всі апроксимації для яких у таблиці 1 наведені лінеаризуючі функції);
- для залежностей, одержання яких вимагає підстанов- ки у вихідну систему лінеаризованних значень KCUi і ti, виконується перерахування KCUi і ti (відповідно до табли- ці 1);
- вирішується вихідна система рівнянь і знаходяться коефіцієнти a і b;
- для залежностей, одержання яких вимагає перераху- вання значень a, b робляться необхідні обчислення (відпо- відно до таблиці 1);
- оцінюється точність апроксимації за середньоквадра-
тичним відхиленням S.
Поліномна (параболічна) регресія:
- визначаються пари значень Xi, Yi;
- розраховуються суми значень
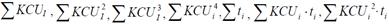
і вирішується система рівнянь
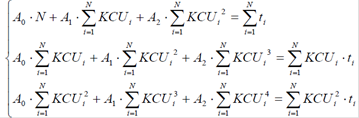
щодо коефіцієнтів A o, A1, A 2;
- оцінюється точність апроксимації вихідних даних параболічною залежністю t(KCU ) = A0+ A1* KCU + A2* KCU2
(за середньоквадратичним відхиленням S).
Виконання вимірів
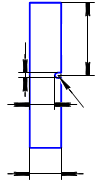
Для проведення досліду на ударний згин використовують стандартні зразки з U-подібним концентратором. Зразок, вільно встановлений на опори копра, руйнується за один удар важкого маятника по стороні, протилежній надрізу. Кількісною характеристикою в'язкості при ударному руйнуванні є ударна в'язкість KCU-відношення роботи A,необхідної для зламу зразка віднесеної до робочої площі поперечного перерізу F:
KCU=A/F
Робота, витрачена на руйнування зразка, розраховується за формулою
А=Рh1(cosβ-cosα),
де Р- маса маятника, кг; h1- відстань від осі маятника до його центра ваги, м; β- кут підйому маятника після руйнування зразка; α- кут підйому маятника перед ударом.
Оскільки Р і h1 постійні для визначеного копра, то KCU можна визначити за визначеними кутами α і β.
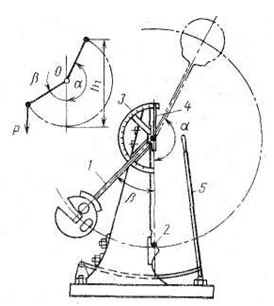

а) б)
8
10

Рисунок 2 - Вимірювання ударної в’язкос а – схема маятни- кового копра: 1 – маятник; 2 – зразок; 3 – шкала; 4 – стрілка шкали; 5 – гальма; б – стандартний зразок для випробувань
Приклад виконання роботи
У ході іспитів стандартних зразків зі сталі, відпущеної при 5 різних температурах (t), одержали 5 пара вимірів ударної в'язкості (KCU)
Таблиця 2 – Результати виміру ударної в'язкості
| Температура відпуску t, 0С
|
| 200
| 300
| 400
| 500
| 600
|
| Ударна в'язкість KCU, Дж/см2
|
| 38
| 47
| 76
| 98
| 125
|
| 39
| 48
| 79
| 97
| 128
|
Установити математичну залежність, що описує з мінімальною похибкою функціональний зв'язок типу t = F(KCU).
Для визначення шуканої залежності використовуємо програму обчислень, складену стосовно до пакета MathCAD.
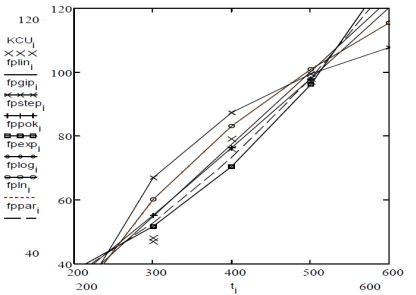
У програмі вихідні дані введені у вигляді двох погоджених масивів KCUi і ti, що являють собою пари значень Xi і Yi. Для зменшення числа повторюваних обчислень формули розрахунку коефіцієнтів a, b і середньоквадратичного відхилення S описані як відповідні їм функції B(X,Y), A(X.Y), S(t,KCUp), що використовуються в програмі під час виконання таких апроксимізаційних розрахунків. Крім того, наприкінці програми на базі вбудованої процедури розв΄язку систем лінійних рівнянь Isolve виконується параболічна апроксимація. Вибір виду регресійної залежності, що описує залежність ударної в’язкості від температури відпуску вибирається за найменшим середньоквадратич- ним відхиленням (згідно з розрахунками обрана параболі- чна регресія, у якої S=3,508). Результати розрахунків ілюструються графіком.
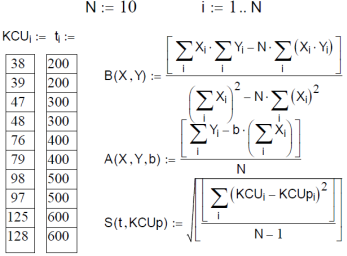
1. Лінійна регресія
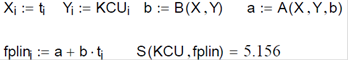
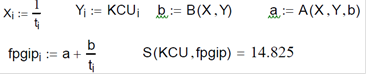 2. Гіперболічна регресія
2. Гіперболічна регресія
3. Ступенева регресія

4. Показникова регресія
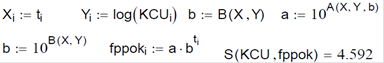
 5. Експонентна регресія
5. Експонентна регресія
6. Логарифмічна регресія 1
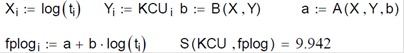
7. Логарифмічна регресія 2
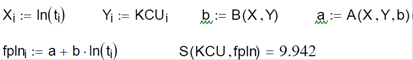
- Параболічна регресія
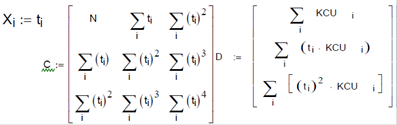
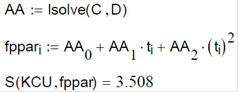
Остаточно беремо параболічну регресію, оскільки їй відповідає найменша дисперсія S=3,508
 Результати розрахунків ілюструємо графіком.
Результати розрахунків ілюструємо графіком.
Вимоги до змісту звіту
Звіт повинен містити:
· Найменування і мету роботи.
· Результати проміжних розрахунків.
· Висновки.
Варіанти завдань
Варіант завдання вибрати відповідно до таблиці 3.
Таблиця 3 – Результати вимірів ударної в’язкості (KCU) при різних температурах відпуску (t)
|
| Перша серія дослідів
| Друга серія дослідів
|
| Варіант 1 сталь 09Г2
|
| Температура відпуску t,0C
|
| 200
| 400
| 500
| 600
| 700
| 200
| 400
| 500
| 600
| 700
|
| Ударна в’язкість KCU, Дж/см2
|
| a
| 57
| 97
| 127
| 185
| 166
| 59
| 99
| 127
| 188
| 167
|
| b
| 56
| 98
| 126
| 186
| 167
| 60
| 100
| 128
| 187
| 166
|
| c
| 60
| 99
| 129
| 187
| 165
| 57
| 98
| 128
| 187
| 169
|
| d
| 61
| 97
| 128
| 188
| 168
| 58
| 98
| 126
| 186
| 166
|
| e
| 59
| 100
| 127
| 186
| 169
| 60
| 97
| 127
| 188
| 167
|
| f
| 58
| 99
| 129
| 184
| 165
| 60
| 98
| 126
| 188
| 168
|
|
| Варіант 2 сталь 14Г2
|
| Температура відпуску t,0C
|
| 200
| 300
| 400
| 500
| 600
| 200
| 300
| 400
| 500
| 600
|
| Ударна в’язкість KCU, Дж/см2
|
| a
| 98
| 88
| 102
| 175
| 197
| 96
| 86
| 104
| 175
| 197
|
| b
| 97
| 87
| 104
| 174
| 196
| 97
| 88
| 102
| 175
| 197
|
| c
| 96
| 86
| 103
| 176
| 195
| 98
| 87
| 103
| 174
| 196
|
| d
| 97
| 89
| 105
| 177
| 198
| 97
| 88
| 103
| 175
| 195
|
| e
| 99
| 90
| 101
| 174
| 199
| 97
| 86
| 104
| 178
| 194
|
| f
| 100
| 88
| 102
| 173
| 196
| 96
| 87
| 104
| 177
| 196
|
| | | | | | | | | | | | |
Продовження табл.3
|
| Перша серія дослідів
| Друга серія дослідів
|
| Варіант 3 сталь 15Х
|
| Температура відпуску t,0C
|
| 200
| 300
| 400
| 500
| 600
| 200
| 300
| 400
| 500
| 600
|
| Ударна в’язкість KCU, Дж/см2
|
| a
| 39
| 47
| 77
| 98
| 126
| 39
| 49
| 80
| 98
| 128
|
| b
| 38
| 48
| 78
| 99
| 127
| 39
| 48
| 80
| 97
| 128
|
| c
| 37
| 49
| 79
| 97
| 129
| 40
| 48
| 79
| 95
| 126
|
| d
| 40
| 50
| 76
| 96
| 128
| 38
| 47
| 79
| 96
| 126
|
| e
| 41
| 51
| 77
| 100
| 127
| 38
| 47
| 75
| 99
| 127
|
| f
| 39
| 49
| 80
| 98
| 126
| 40
| 48
| 76
| 97
| 128
|
|
| Варіант 4 сталь20Х
|
| Температура відпуску t,0C
|
| 200
| 300
| 400
| 500
| 600
| 200
| 300
| 400
| 500
| 600
|
| Ударна в’язкість KCU, Дж/см2
|
| a
| 118
| 146
| 176
| 197
| 224
| 117
| 149
| 176
| 196
| 226
|
| b
| 120
| 147
| 175
| 196
| 225
| 116
| 148
| 177
| 197
| 225
|
| c
| 117
| 148
| 177
| 195
| 226
| 119
| 149
| 175
| 197
| 224
|
| d
| 116
| 149
| 176
| 198
| 227
| 118
| 145
| 176
| 195
| 224
|
| e
| 119
| 147
| 178
| 197
| 223
| 117
| 146
| 176
| 195
| 227
|
| f
| 118
| 145
| 176
| 196
| 224
| 118
| 149
| 177
| 195
| 226
|
|
| Варіант 5 сталь 40Х
|
| Температура відпуску t,0C
|
| 200
| 300
| 400
| 500
| 600
| 200
| 300
| 400
| 500
| 600
|
| Ударна в’язкість KCU, Дж/см2
|
| a
| 28
| 21
| 48
| 68
| 146
| 30
| 19
| 50
| 70
| 147
|
| b
| 30
| 20
| 47
| 69
| 147
| 28
| 20
| 49
| 69
| 146
|
| c
| 29
| 19
| 49
| 70
| 148
| 30
| 21
| 48
| 68
| 145
|
| d
| 27
| 18
| 50
| 67
| 147
| 30
| 20
| 49
| 69
| 145
|
| e
| 30
| 22
| 51
| 68
| 146
| 28
| 19
| 49
| 70
| 146
|
| f
| 28
| 20
| 48
| 70
| 148
| 30
| 19
| 50
| 68
| 146
|
Практикум №8. МЕТОДИ ПЛАНУВАННЯ ЕКСПЕРИМЕНТІВ ПРИ РОЗРОБЛЕННІ СКЛАДУ ВИСОКОМІЦНОГО СПЛАВУ
Мета роботи - вивчення методики планування бага- тофакторних експериментів наприклад, при розробленні складу високоміцного твердого сплаву для обробки деталей, що дають зливну стружку
Загальні положення
Однією з найбільш важливих характеристик твердих сплавів є межа міцності при вигині, оскільки вони характеризуються крихкістю й досить малою пластичністю, а тому відповідно низьким опором і ударним навантаженням.
Тверді сплави WC-Co призначені переважно для обробки матеріалів, що дають стружку надламу. Очевидно, що для одержання матеріалу для бробки деталей, що дають зливну стружку, необхідно використовувати додаткові добавки. Найбільше підходять для вирішення даного завдання карбід Ti (Ti) і карбід Ta (Ta):
Ti - поліпшує стійкість проти окиснювання, твердість і жароміцність;
Ta - сприяє зменшенню зерна, загальмовуючи в такий спосіб рекристалізацію карбідної фази, а також зменшує здатність до зварювання матеріалу зі стружкою.
Важливим фактором, що впливає на межу міцності при вигині, є розмір зерна, тому його необхідно теж урахувати. На властивості сплаву може впливати і наявність Nb, що потрапляє з руди Та.
Щоб передбачити властивості міцності розроблюваного матеріалу, необхідно знати математичну модель. Побудувати її можна, провівши відповідні одно факторні експерименти з визначення залежності межі міцності при вигині від кожного з факторів (складових). При цьому необхідно один із факторів (наприклад, кількість певної складової) змінювати в певних межах (всі інші фактори стабілізуються) і оцінювати як при цьому буде змінюватися межа міцності при вигині. Нескладна статистична обробка, наприклад, з використаннями методу найменших квадратів дозволяє одержати математичну залежність межі міцності при вигині від змінюваного фактору. Повторивши експерименти для всіх факторів можна в остаточному висновку, визначити залежність межі міцності при вигині від усіх факторів окремо й потім побудувати загальну математичну модель. Однак при великій кількості факторів час на побудову моделі й витрати на проведення всієї серії експериментів можуть бути настільки значними, що здійснення їх стане нереальним. У цьому випадку використовують методику проведення багатофакторних експериментів.
Сутність методики багатофакторного експерименту полягає в тому, що при його проведенні змінюється не один фактор, а відразу всі, причому їхня зміна не довільна, а виконується за певним планом. План проведення багатофакторного експерименту складається таким чином, щоб шляхом відповідної математичної обробки виділити вплив кожного фактору і, як наслідок, скласти модель сплаву.
Проведення багатофакторного дослідження можливе, якщо дотримуються такі вимоги до методики розробки складу твердого сплаву:
- змінюваний фактор повинен бути: а) керованим, тобто дозволяти експериментаторові встановлювати необхідне значення фактору й підтримувати постійним це значення протягом досліду; б) незалежним - повинна бути можливість установлення фактору на будь-якому рівні незалежно від рівнів інших факторів; в) однозначним - не бути функцією інших факторів; г) сумісним - можливий взаємний вплив факторів не повинен приводити до неможливості отримання сплаву; д) реалізованим - межі зміни факторів повинні забезпечувати можливість їхньої фізичної реалізації.
- вимірювання межі міцності при вигині повинне дозволяти: а) визначати межу міцності при вигині при будь- якій зміні (комбінації) факторів, і ця зміна повинна бути контрольованою; б) оцінювати числове значення межі міцності при вигині з високою точністю, тобто контроль межі міцності при вигині повинен бути статистично ефективним.
Методика виконання роботи
Побудова плану проведення експерименту
Оскільки фактори неоднорідні й мають різні одиниці виміру, а числа, що виражають величини факторів, мають різні порядки, їх треба перед побудовою плану експерименту привести до єдиної системи числення шляхом переходу від дійсних значень факторів до кодованого за формулами:
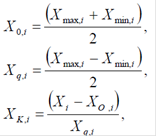
де XO,i - основний рівень; Xq,i - інтервал варіювання;
Xk,i - кодоване значення фактору;
Xmax,i - верхній рівень. Кодоване значення верхнього рівня «+1» (у плані експерименту цифрою «1» нехтуємо й звичайно записуємо тільки знак «+»);
Xmin,i - нижній рівень. Кодоване значення нижнього рівня «-1» (у плані експерименту записується знак «-»).
Багатофакторний експеримент може виконуватися за планом повного факторного експерименту (число досвідів N = 2K, де К - загальне число факторів дослідження) або дробового факторного експерименту (N = 2K+P, де Р - число лінійних ефектів). Повний факторний експеримент доцільно проводити в тому випадку, якщо він за часом нетривалий і вимагає невеликих витрат, тому що при однаковому числі факторів кількість дослідів для побудови математичної моделі значно більше, ніж при дробовому факторному експерименті.
Дробовий факторний експеримент проводиться при числі факторів від двох і більше за умови, якщо повний факторний експеримент з економічних міркувань проводити невигідно.
Побудова плану повного факторного експерименту
Побудова плану повного факторного експерименту зводиться до стандартної форми запису умов проведення експериментів у вигляді таблиці, у стовпчиках якої записуються всі можливі поєднання досліджуваних факторів у кодах «+» і «-»). Позначають стовпчики змінної X, що відповідає певному фактору. Наприклад, X1 - перший фактор – зміст WC, X2 - другий фактор – зміст Ti і т.д.
Записують фактори в таблицю, починаючи із другого стовпчика (першому стовпчику завжди відповідає фіктивний фактор, позначений через X0). При цьому в першому стовпчику таблиці записуються всі знаки "+", у другому стовпчику необхідно змінювати знаки по черзі, у третьому чергувати через два, у четвертому - через чотири, у п'ятому - через вісім і т.д. за ступенями двійки. Після того, як вичерпані всі варіанти зміни факторів, переходять до комбінацій їхніх взаємодій. Для цього вводять стовпчики з комбінаціями добутків факторів X1
X2,X1X3,X1X4…X1Xn,X2X3,X2X4…X2Xn…X1X2X3,X1X2X4
…X1X2Xn…X2X3X4,X2X3Xn…X1X2X3X4……X1X2X3…Xn..
Оскільки змінні X1,X2…Xn набувають значення «+1» і «-1», то добутки змінних наберуть тих самих значень «+1» і «-1» .
У таблицях 1–3 показані зразки побудови планів експериментів при числі факторів 1,2,3. У таблицях порядково записані кодові значення змінних, які вони повинні приймати в кожному з дослідів експерименту, при їхній загальній кількості, що дорівнює, відповідно 2,4,8. (Наприклад, при проведенні досліду номер 2 за планом таблиці 3 значення факторів Х2, Х3 і взаємодій Х1Х2, Х1Х3 мають кодове значення «-1» і повинні бути мінімальними, а значення фактора Х1 і взаємодій Х2Х3, Х1Х2Х3 мають кодові значення «+1» і повинні бути максимальними).
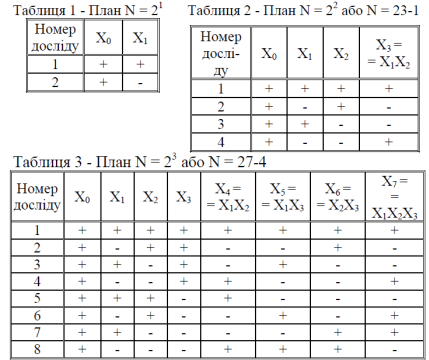
Побудов а плану дробового факторного експерименту.
План дробового факторного експерименту складається на основі плану повного факторного експерименту, коли відомо, що між деякими факторами відсутній ефект взаємодії. У цьому випадку замість несуттєвої взаємодії записується новий фактор, і значення нового фактора в умовах дослідів визначаються за знаками, зазначеними у відповідному стовпчику. Наприклад, якщо відомо, що немає взаємодії факторів Х1Х2 у плані повного факторного експерименту N = 23, то цю взаємодію можна замінити фактором Х4 і буде отримано план дробового факторного експерименту N = 24-1. Якщо несуттєва взаємодія Х1Х3, його також можна замінити фактором Х4, а якщо несуттєві обидві ці взаємодії, то можна в план експерименту включити два додаткових фактори Х4 і Х5.
Усього на базі плану N = 23 можна побудувати план дробового факторного експерименту, що дозволить досліджувати склад сплаву відразу по семи факторах (див. табл. 3, де Х4=Х1Х2, Х5=Х1Х3 , Х6=Х2Х3 Х7=Х1Х2Х3).
На базі плану N =24 можна досліджувати склад і побудувати модель, що включає до 31 фактора, провівши при цьому 32 досліди. У загальному випадку як підходящий дробовий факторний експеримент варто брати повний факторний експеримент, число досвідів у якому більше, ніж число факторів у досліджуваному складі сплаву.
Перевірк а властивостей планів повного і дробового факторного експериментів
Після побудови плану експерименту необхідно перевірити його властивості:
- симетричність плану щодо центру експерименту -алгебраїчна сума елементів кожного стовпчика, крім першого, що відповідає фіктивній змінній, повинна бути такою, що дорівнює нулю:
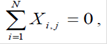
де i - номер досліду (номер рядка),
j - номер фактора (номер стовпця), j=1,2, ... К;
- нормування - сума квадратів елементів кожного стовпчика дорівнює числу дослідів:
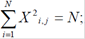
- ортогональність - сума порядкових добутків елементів будь-яких двох стовпчиків дорівнює нулю
N
å X i , j ´ X i , j + m = 0,
i =1
де m - довільне ціле число, що задовольняє умову j+m<К. Якщо план експерименту відповідає переліченим властивостям, то він вважається ротатабельным, тобто математична модель, отримана у результаті експерименту з таким планом, здатна передбачити значення межі міцності при вигині з однаковою точністю в будь-яких напрямках на рівних відстанях від центру плану.
Пров е денн я експерименту
Перед проведенням експерименту необхідно рандомізувати його план, тобто призначити проведення дослідів у випадковій послідовності. Для розміщення номерів дослідів у випадковій послідовності можна скористатися таблицями рівномірно розподілених випадкових величин, генератором випадкової величини комп'ютера або будь-яким іншим методом (наприклад, написати номери дослідів на листках паперу, перевернути, перемішати аркуші паперу й брати їх у випадковій послідовності).
Для підвищення точності експерименту його повто рюють кілька разів (не менше двох). При цьому досліди кожної серії експериментів також повинні бути рандомізовані.
У таблиці 4 показаний приклад побудови плану дробового факторного експерименту 23-1, що передбачає три серії дослідів, і в кожній серії досліди виконуються у випадковій послідовності. Відповідно до цієї таблиці першим повинен виконуватися другий дослід з першої серії експериментів (другий фактор (складова) Х2 установлюється на верхньому рівні, перший і третій фактори – на нижньому рівні). У результаті проведення досліду буде отриманий вихідний параметр (межа міцності при вигині, позначена як Y21 ). Потім третій дослід першої серії (X1,max, X2,min, X3,min, результат Y31), перший дослід (X1,max, X2,max, X3,max – Y11) і четвертий дослід (X1,min, X2,min, X3,max -Y41). Після завершення першої серії дослідів виконуються другий (третій, перший, четвертий, другий досліди з результатами Y32, Y12, Y42, Y22) і третя серія дослідів (четвертий, перший, другий, третій досліди).
Таблиця 4 - Повний план виконання дробового факторного експерименту 2( 3-1)
|
Но- мер дос- ліду
| Серія
|
Х0
|
Х1
|
Х2
|
Х3
| Результати дослідів за серіями
|
| 1
| 2
| 3
|
| Порядок виконання дослідів
|
1
|
2
|
3
|
| 1
| 3
| 2
| 2
| +
| +
| +
| +
| Y11
| Y12
| Y13
|
| 2
| 1
| 4
| 3
| +
| -
| +
| -
| Y21
| Y22
| Y23
|
| 3
| 2
| 1
| 4
| +
| +
| -
| -
| Y31
| Y32
| Y33
|
| 4
| 4
| 3
| 1
| +
| -
| -
| +
| Y41
| Y42
| Y43
|





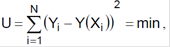

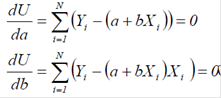
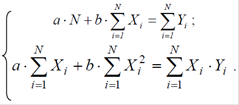
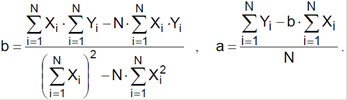
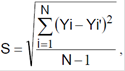

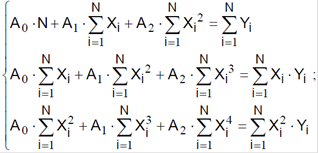
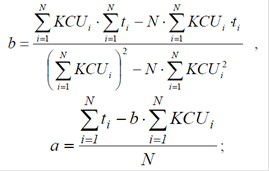
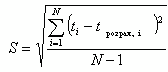
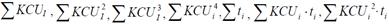
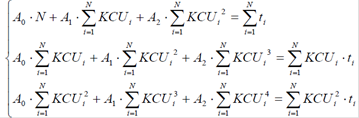


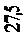 а) б)
а) б)

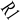 8
8
 Рисунок 2 - Вимірювання ударної в’язкос а – схема маятни- кового копра: 1 – маятник; 2 – зразок; 3 – шкала; 4 – стрілка шкали; 5 – гальма; б – стандартний зразок для випробувань
Рисунок 2 - Вимірювання ударної в’язкос а – схема маятни- кового копра: 1 – маятник; 2 – зразок; 3 – шкала; 4 – стрілка шкали; 5 – гальма; б – стандартний зразок для випробувань

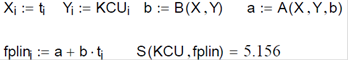
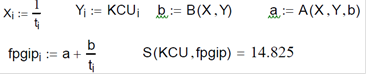 2. Гіперболічна регресія
2. Гіперболічна регресія
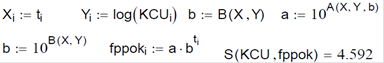
 5. Експонентна регресія
5. Експонентна регресія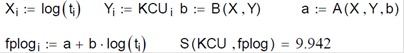
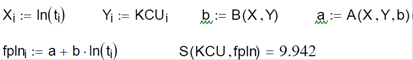
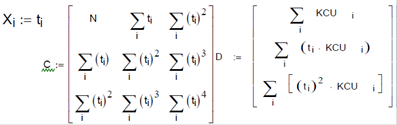
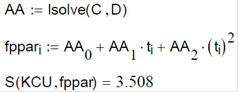
 Результати розрахунків ілюструємо графіком.
Результати розрахунків ілюструємо графіком.