Мета роботи - вивчення методики застосування ге- нетичних алгоритмів для визначення параметрів прохо- дження дифузійних процесів.
Загальні положення
Генетичні алгоритми, як правило, застосовуються для оптимізації цільової функції у задачах комбінаторного типу, коли для пошуку розв’язку найкращим або єдиним способом є перебір аргументів цільової функції. При цьому сам процес рішення здійснюється без втручання проектувальника і ґрунтується на випадкових подіях, описати які можна в термінах еволюційного розвитку.
Залежно від характеру розв'язуваної задачі генетичні алгоритми можуть містити різні етапи, що є математичними аналогами відповідних механізмів, що беруть участь у еволюційному розвитку. У більшості своїх реалізацій генетичний алгоритм включає уточнення цільової функції, створення початкової популяції, вибір батьків, схрещуван ня особин, мутацію нових особин, добір і знищення слабких особин, перевірку якості нової популяції. Процеси від створення нової популяції до перевірки її якості циклічно повторюються до того часу, поки не буде досягнутий оптимум цільової функції або поки не відбудеться встановлене число змін поколінь.
Вибір цільової функції обумовлений змістом задачі, розв'язуваної з використанням генетичних алгоритмів. При дослідженні дифузійних процесів звичайно прагнуть побудувати математичну модель, яка б повною мірою описувала процес дифузії. Оптимумом цільової функції є мінімальне відхилення значень концентрації експериментальних даних від теоретичних.
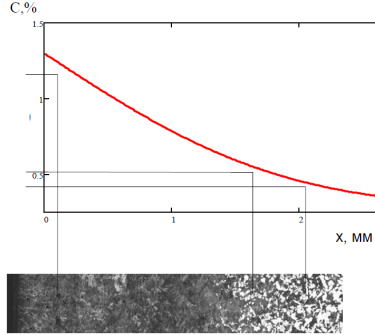
Дослідник проводить виміри товщини дифузійних зон металографічним шляхом при відомих значеннях концентрації компонентів у них (рисунок 1).
Сутність застосування генетичного алгоритму полягає у тому, що, зіставляючи різні довжини дифузійних шарів, при відомій концентрації і підбираючи коефіцієнт дифузії, вибирається оптимум – експериментальні дані, що описують процес дифузії більш повно.
Створення нової популяції на початку еволюційного періоду має на увазі формування множини λo ={λ01, λ02 ,…λ0N} з N векторів, кожний з яких формується випадково і відображає геном конкретної особини, що складає вихідну популяцію.
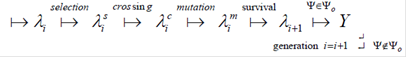 Процес пошуку рішення являє собою послідовну зміну популяцій. Перехід від популяції λ0 до Λ1 і потім послідовно від λ i до λ i+1 проходить шляхом поетапного застосування обраних механізмів репродукції і порівняння якості нових популяцій з критеріями оптимальності:
Процес пошуку рішення являє собою послідовну зміну популяцій. Перехід від популяції λ0 до Λ1 і потім послідовно від λ i до λ i+1 проходить шляхом поетапного застосування обраних механізмів репродукції і порівняння якості нових популяцій з критеріями оптимальності:
 де selection, crossing, mutation і survival – відповідно оператори відбору, схрещування, мутації та виживання.
де selection, crossing, mutation і survival – відповідно оператори відбору, схрещування, мутації та виживання.
Рисунок 1 – Розподіл концентрації вуглецю у структурних зонах зразка
У ролі оператора відбору використовується механізм випадкового відбору, що базується на тому, що більш життєздатна особина має найбільшу ймовірність брати участь у формуванні нащадків. Це означає, що чим ближче сумарна різниця відхилень значень концентрації, що складають геном особини, до критерію оптимальності цільової функції, тим вище ймовірність участі такої особини у створенні потомства. Отже, можна припустити, що ймовірність утворення потомства повинна бути пропорційною якості особини, що відбирається, і вона може брати участь в утворенні декількох батьківських пар.
Сутність дії оператора схрещування полягає в тому, що він повинен забезпечити обмін генами між двома особинами, що утворять батьківську пару. Оператор схрещування може бути одно-, дво- або багатокрапковим. При однокрапковому схрещуванні випадковим чином визначається номер координати tÎ{1,…,n-1}, названої крапкою розриву, де n – довжина вектора λ, і виконується обмін генами батьківських пар, починаючи з t+1 гена до n включно:
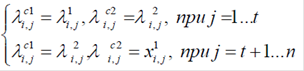
При двокрапковому операторі схрещування вибирається не одна, а дві крапки розриву t1 і t2, після чого проводиться обмін генами на ділянках векторів λ1,i і λ 2,i від t1-ї до t2-ї координати включно:
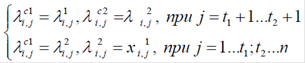
Аналогічно реалізуються і багатокрапкові оператори схрещування.
Оператори схрещування з декількома крапками розриву часто застосовують у тих задачах, де існують особливі правила формування геному особи. Крім того, для створення життєздатних особин (з геномом, що задовольняє встановленим особливим правилам) багатокрапковий оператор схрещування може бути доповнений засобами штуч- ної мутації, механізм якої вибирається відповідно до конкретних вимог до формування геному.
У загальному випадку оператор мутації служить для моделювання природного процесу мутації, покликаний розширити аналізований генофонд і тим самим перешкоджати багаторазовому повторенню поколінь з геномоподібними особинами (зацикленню задачі).
В операторі мутації, також як і двокрапковому операторі схрещування, випадковим чином визначаються дві крапки розриву вектора λ i, а потім виконується обмін між двома генами з координатами t1 і t2. Ймовірність застосування оператора мутації береться малою, а у випадку його спрацьовування виконується зміна геному особини відповідно до правила
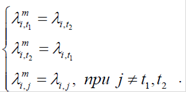
Послідовне застосування операторів добору, схрещування і мутації приводить до створення нових особин, що разом з особинами вихідної популяції складають нову, розширену популяцію, що складається з удвічі більшого числа особин. У зв'язку з цим виконується добір найбільш сильних особин, а загальна чисельність нової популяції доводиться до спочатку встановленого рівня шляхом знищення слабких особин. При цьому працює оператор виживання, в основі якого лежить механізм визначення якості особини за показниками критерію оптимальності. Особина найгіршої якості виключаються з популяції. У деяких модифікаціях оператора виживання імовірність знищення особини ставиться у відповідність до її якості.
Роботою оператора виживання закінчується репродуктивний цикл і у випадку, якщо рішення не отримане, він повторюється стосовно нової популяції відповідно до встановленого генетичного алгоритму.
Методика виконання роботи
Даними для аналізу дифузійних процесів є результати практичних досліджень щодо встановлення глибини дифузійного шару. (Приклад методики виміру глибини дифузійного шару наведений у практичній роботі «Оцінка анормальності результатів вимірювань при контролі глибини дифузійного хромованого кулі сталі 4Х5МФ1С»).
1) Спираючи на експериментальні дані, складають вихідну популяцію з заданого числа особин.
Вихідну популяцію представляють у вигляді обмеженої безлічі λo, що включає N векторів λ o:
λo ={λ01, λ0 , …, λ0N},
тобто під популяцією розуміють безліч λo, що є відомою концентрацією на межі кожної обумовленої дифузійної зони. Кожна особина популяції λi відображає один з варіантів вимірювання розподілу глибини дифузійного шару.
Як геном особини беруть довжину структурних шарів, що входять в оптимізовану ділянку розподілу концентрації:

де Pi,k – довжина шару k-ї концентрації.
n – число експериментально отриманих даних.
2) Відбирають батьківські пари, що будуть використані для генерації особин нової популяції.
В операторі добору вірогідні оцінки участі особин у схрещуванні беруть пропорційними їх якості. Для цього в кожної особини з отриманої популяції визначають значення цільової функції F:
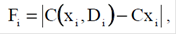
де С(xi,Di) – закон розподілу концентрації дифузійного шару;
Схi – концентрація, отримана металографічним аналізом.
Потім встановлюють імовірність участі особини в розмноженні. Для цього розраховують коефіцієнти
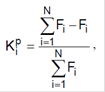
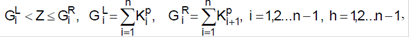 та визначають межі інтервалів, що відповідають найбільшої ймовірності включення особини в пару:
та визначають межі інтервалів, що відповідають найбільшої ймовірності включення особини в пару:
розігрують випадкову величину Z з будь-якими значеннями від 0 до 1, і якщо випадкова величина відповідає розрахованій імовірності (попадає в інтервал), то особину включають у батьківську пару.
Участь другої особини в батьківській парі розігрують аналогічним чином. При цьому якщо номер, що має особина у популяції, збігається з уже розіграним номером (тобто визначена та сама особина), тобто таку особину не включають у пару і розігрування другої особини батьківської пари повторюють.
Розігрування батьківських пар виконують до того часу, поки загальне число особин, що складають батьківські пари, не стане такою, що дорівнює числу всіх особин вихідної популяції. Одночасно з цим не накладається ніяких обмежень на число пар, у створенні яких може брати участь кожна з особин.
3) Виконують схрещування й одержують особини нової популяції.
Для схрещування використовують двокрапковий оператор схрещування, відповідно до якого відбирають дві випадкові цілі величини, значення яких не можуть збігатися і повинні знаходитися в інтервалі від 2 до n-1. Розіграні випадкові величини перемішують та приймають меншу як першу крапку розриву t1, а велику – як другу крапку розриву t2.
Схрещування виконують таким чином, щоб особини обмінювалися генами на ділянках від 1-го гена до гена з координатою t1 і від гена з координатою t2 до кінцевого гена, а гени на ділянці від t1 до t2 залишалися б незмінними:
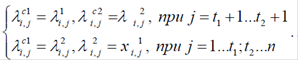
4) Перевіряють імовірність застосування оператора мутації і відповідно до неї використовують оператор мутації. Для цього задають імовірність мутації у межах від 0,001 до 0,01 (від 0,1 до 1%). Потім відбирають випадкову величину, значення якої може змінюватися від 0 до 1 і якщо результат розігрування не перевищує заданий рівень ймовірності, то застосовують оператор мутації. У протилежному разі переходять до наступного етапу виконання роботи.
Перед застосуванням оператора мутації спочатку вста- новлюють особину, що повинна бути піддана мутації. Для цього визначають номер такої особини в популяції – як результат розігрування цілої випадкової величини, що може змінюватися від 1 до n.
Потім до обраної особини застосовують оператор му- тації, відповідно до якого відбирають дві випадкові цілі величини t1 і t2, значення яких не збігаються і повинні бути в інтервалі від 1 до n. Беручи ці випадкові величини як координати мутованих генів, виконують обмін генами всередині геному особини відповідно до правила
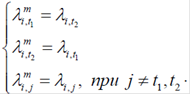
5) Формують нову популяцію з числом особин, що дорівнює числу особин вихідної популяції.
Спочатку в нову популяцію включають усі існуючі особини вихідної популяції і додатково особини, знов згенеровані операторами схрещування і мутації.
Розраховують значення цільової функції F для знову створених особин нової популяції (для особин вихідної популяції такий розрахунок уже виконаний) і потім відповідно до оператора виживання з популяції виключають особини з найбільшими розрахунковими значеннями цільової функції. Число особин, що видаляються, вибирають таким чином, щоб розмір нової популяції став рівним розміру вихідної популяції.
6) Перевіряють досягнення оптимуму.
Про перебування оптимального рішення свідчить значення цільової функції F>0. Якщо оптимум досягнутий, то рішення припиняють.
Якщо оптимальне рішення не знайдене, то стосовно знову сформованої популяції послідовно застосовують оператори добору, схрещування, мутації і виживання (пп.2-5). Таке циклічне виконання операторів повторюють до того часу, поки не буде досягнутий оптимум цільової функції (F>0) або ж не пройде встановлений еволюційний період (число змін поколінь досягне встановленого рівня).
Приклад виконання роботи
Вихідними є умови проходження процесу дифузії:
- час витримки дорівнює 20 год, t = 72000 с;
- концентрація вуглецю на поверхні зразка Cs=1,3%;
- концентрація вуглецю у серцевині зразка (відповідає марці сталі) C0=0,28%;
- закон розподілу концентрації вуглецю від товщини дифузійного шару:
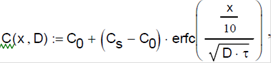
де х – відстань, що вимірюється від початку відліку до глибини вимірюваної зони, мм (див. рисунок 1);
- розподіл концентраційних зон, чітко видних за допомо-
гою мікроскопа:
Cx := ( 0.83 0.6 0.45 0.28 ).
З експериментальних даних з кожного виміру визначаємо довжину структурної зони і складаємо вихідну популяцію:
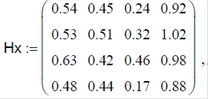
Тоді xi = å Hxi
Коефіцієнт дифузії розраховуємо за чотирма обраними випадковим чином довжинами дифузійних зон:
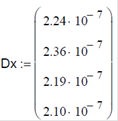
Далі знаходимо значення відхилень цільової функції
для кожного значення вихідної популяції:
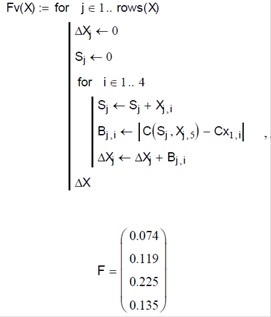
де Х – матриця, отримана з’єднанням матриць Нх та Dx
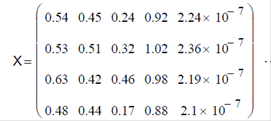
Потім визначаємо імовірність участі особи у схрещуванні:
 де Z – дискретні значення цільової функції (матриця F).
де Z – дискретні значення цільової функції (матриця F).
Вибираємо пари для схрещування так, щоб не схрещувати особину саму із собою.

Випадковим чином робимо вибір точок розриву і фо-
рмуємо нову популяцію.

Робимо обмін парами генів:
W1 := det (p1 , p2)
W2 := det (p3 , p4) .
Зводимо у таблицю нову популяцію, що включає батьківські і дитячі особини:
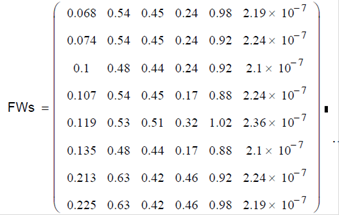
Застосовуємо оператор виживання і формуємо нову популяцію, що включає найбільш життєздатні батьківські і дитячі особини
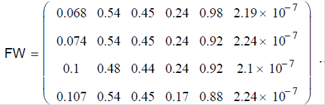
Цільові функції особин нової популяції ближче до оптимуму і, отже, вона є кращою, ніж вихідна. У той же час для першої, найкращої особини нової популяції значення цільової функції Fi =>0, що свідчить про відсутність оптимуму (розрахункове значення концентрації й отримане металографічним аналізом не збігається). У зв'язку з цим еволюційний цикл варто повторити.
Вимоги до змісту звіту
Звіт повинен містити:
1. Найменування і ціль роботи.
2. Результати проміжних розрахунків.
3. Висновки.
Варіанти завдань
Варіанти завдань поданi в таблицях 1-3.
Приклад завдання для варіанта 1а:

Таблиця 1 – Розподіл концентрації на границях структурних зон
|
Пiдварiант
| Концентрація вуглецю на границях зон, %
|
| 1
| 2
| 3
| 4
| 5
|
| a
| 1.31
| 0.82
| 0.67
| 0.43
| 0.25
|
| b
| 1.42
| 0.85
| 0.7
| 0.4
| 0.2
|
| c
| 1.2
| 0.81
| 0.6
| 0.38
| 0.18
|
| d
| 1.23
| 0.8
| 0.55
| 0.43
| 0.15
|
| e
| 1.37
| 0.9
| 0.68
| 0.5
| 0,1
|
| f
| 1.33
| 0.82
| 0.63
| 0.48
| 0.3
|
Таблиця 2 –Розрахунковий коефіцієнт дифузії
|
Варіант
| Номер виміру
|
| 1
| 2
| 3
| 4
|
| 1
| 2.25 х10-7
| 2.39 х10-7
| 2.36 х10-7
| 2.11 х10-7
|
| 2
| 2.15 х10-7
| 2.24 х10-7
| 2.18 х10-7
| 2.41 х10-7
|
| 3
| 2.2 х10-7
| 2.31 х10-7
| 2.33 х10-7
| 2.51 х10-7
|
| 4
| 2.05 х10-7
| 2.13 х10-7
| 2.16 х10-7
| 2.34 х10-7
|
| 5
| 2.32 х10-7
| 2.29 х10-7
| 2.17 х10-7
| 2.25 х10-7
|
Таблиця 3 - Обмірювані довжини структурних зон
| Варіант
| Обмірювані довжини
|
| Структурна зона
1
| Структурна зона
2
| Структурна зона 3
| Структурна зона
4
|
| Номер виміру
|
| 1
| 2
| 3
| 4
| 1
| 2
| 3
| 4
| 1
| 2
| 3
| 4
| 1
| 2
| 3
| 4
|
| 1
| 0.52
| 0.54
| 0.61
| 0.47
| 0.44
| 0.52
| 0.4
| 0.42
| 0.23
| 0.31
| 0.28
| 0.18
| 0.93
| 0.95
| 0.94
| 0.97
|
| 2
| 0.51
| 0.6
| 0.62
| 0.55
| 0.5
| 0.52
| 0.43
| 0.47
| 0.32
| 0.29
| 0.3
| 0.31
| 0.92
| 0.96
| 0.93
| 0.9
|
| 3
| 0.48
| 0.55
| 0.67
| 0.7
| 0.61
| 0.56
| 0.42
| 0.43
| 0.33
| 0.27
| 0.32
| 0.31
| 0.89
| 0.84
| 0.87
| 0.78
|
| 4
| 0.52
| 0.59
| 0.56
| 0.5
| 0.54
| 0.48
| 0.47
| 0.52
| 0.29
| 0.34
| 0.32
| 0.31
| 0.79
| 0.8
| 0.82
| 0.81
|
| 5
| 0.53
| 0.58
| 0.6
| 0.61
| 0.43
| 0.4
| 0.38
| 0.45
| 0.25
| 0.29
| 0.31
| 0.33
| 0.75
| 0.82
| 0.73
| 0.74
|





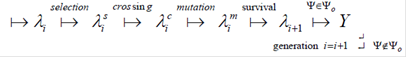 Процес пошуку рішення являє собою послідовну зміну популяцій. Перехід від популяції λ0 до Λ1 і потім послідовно від λ i до λ i+1 проходить шляхом поетапного застосування обраних механізмів репродукції і порівняння якості нових популяцій з критеріями оптимальності:
Процес пошуку рішення являє собою послідовну зміну популяцій. Перехід від популяції λ0 до Λ1 і потім послідовно від λ i до λ i+1 проходить шляхом поетапного застосування обраних механізмів репродукції і порівняння якості нових популяцій з критеріями оптимальності: де selection, crossing, mutation і survival – відповідно оператори відбору, схрещування, мутації та виживання.
де selection, crossing, mutation і survival – відповідно оператори відбору, схрещування, мутації та виживання.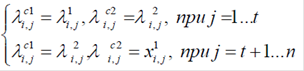
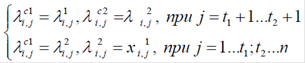
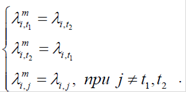

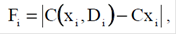
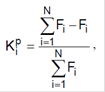
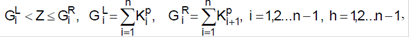 та визначають межі інтервалів, що відповідають найбільшої ймовірності включення особини в пару:
та визначають межі інтервалів, що відповідають найбільшої ймовірності включення особини в пару: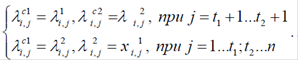
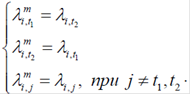
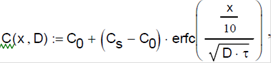

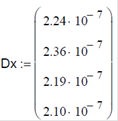
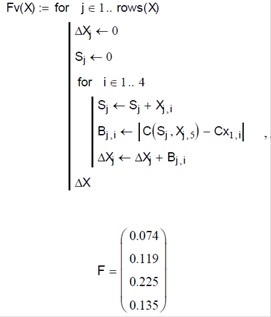

 де Z – дискретні значення цільової функції (матриця F).
де Z – дискретні значення цільової функції (матриця F).






