Подсчет длины и объема веревки

Первый шаг – подсчет суммарной площади A всех внешних поверхностей судна, которая равна площади днища B плюс площадь крыши R плюс площадь стенок W

Площадь днища B нам известна, она равна 1 ikû, или 12 960 000 п 2, или 3600 м2. Площадь крыши R мы приняли равной B. Остается вычислить площадь стенок W; для этого нам понадобится

Первая теорема Паппа о центроиде (иначе, о площади поверхности вращения): Площадь поверхности вращения, образованной вращением плоской кривой вокруг не пересекающей ее оси, лежащей в одной с ней плоскости, равна произведению длины кривой на длину окружности с радиусом, равным расстоянию от этой оси до центроида (барицентра, центра тяжести) этой кривой [192].

В нашем случае «плоская кривая» из теоремы Паппа – это поперечный полуэллиптический профиль стенки нашего судна; пусть L –  его длина (одна из величин, которую нам надо вычислить). Геометрически всю стенку можно считать результатом вращения полуэллипса вокруг вертикальной оси, проходящей через центральную точку днища; соответственно, нам надо будет вычислить расстояние центра тяжести нашего полуэллипса от оси вращения, чтобы затем получить длину M пробегаемой им окружности. Тогда по теореме Паппа поверхность стенок будет равна W = L× M.

Вычисление длины периметра эллипса (или его части) в общем случае представляет собой весьма сложную и громоздкую процедуру[193]. К счастью, имеются приближенные формулы. В нашем случае, поскольку мы приняли ширину полуэллипса равной V его высоты (т. е. полный эллипс имеет малую ось b вдвое короче большой оси a), по формуле Рамануджана[194], дающей результат с точностью до трех десятичных знаков[195], получаем:

 

 

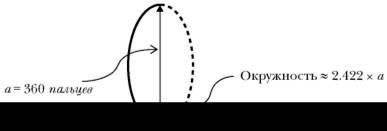
Здесь a – высота стенок (1 нд или 360 п), а поскольку нас интересует длина лишь полупериметра этого эллипса, получаем L ≈ ½ ×2,422 × 360 = 436 n.

Теперь перейдем к вычислению длины M окружности, пробегаемой центром тяжести нашего полуэллипса при его вращении вокруг оси, проходящей через центр днища. Радиус R этой окружности – это радиус r днища плюс расстояние d, на которое центр тяжести периметра полуэллипса (т. е. поперечного профиля выпуклой стенки) отстоит от (воображаемой) вертикальной цилиндрической стенки, идущей строго вдоль края днища. Площадь днища S нам сообщена в Табличке Ковчега – она равна 1 ikû; из формулы S = π×r2 получаем (округляя до ближайшего целого числа пальцев):

r = √ (S/π) = √ (12 960 000 n2 / π) ≈ 2031 n.

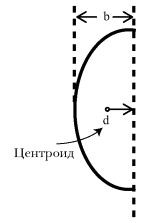
Добавочная величина d есть расстояние от центра тяжести полуэллиптической дуги до большой оси эллипса; она получается по формуле[196]

d = 2b / π,

подставляя в которую значение b = ¼ нд = 180 n, получаем d ≈ 57 n.

 

 

По знакомой всем формуле «Окружность = 2π× Радиус» вычислим длину M искомой окружности с радиусом r + d:

D = 2π× (r + d) = 2π × 2088 п ≈ 13 119 п.

Теперь, наконец, мы можем по Первой теореме Паппа вычислить площадь W стенок коракла:

W= L × M ≈ 436 п × 13 119 п ≈ 5 719 880 п 2,

а затем и суммарную площадь всех его поверхностей (днище + крыша + стенки):

A = B + R + W ≈ 12 960 000 + 12 960 000 + 5 719 880 ≈ 31 639 880 n2

(т. е. 2,44135 ikû или 8789 м2).

Займемся теперь вычислением количества (объема) веревки, требующегося для того, чтобы сплести наш коракл. Будем считать, что ряды веревки притянуты друг к другу настолько плотно, что в каждом ряду поперечное сечение веревки с пренебрежимой погрешностью приближается к квадрату. Также, поскольку толщина плетения повсюду одинаковая (1 палец) и пренебрежимо мала по сравнению с площадью плетеных поверхностей, суммарный объем использованной веревки мы можем получить, помножив только что вычисленную суммарную площадь поверхностей на их толщину в 1 п – опять же с пренебрежимой погрешностью.

Таким образом, вычисленный объем Vc всей веревки, требуемой для того, чтобы сплести остов Ковчега, равен

Vc = 1 п (толщина) x 31 639 880 п 2 = 31 639 880 п 3.

Это – объем в кубических пальцах; разделив его на 2160 (столько п3 содержится в 1 sûtu), получим

 

Vc = 14 648 sûtu.

 

Сравним вычисленную нами величину с той, что бог Энки назвал Атрахасису:

Vg = 14 430 sûtu.

 

Она отличается от нашей менее чем на полтора процента. Этот потрясающий результат свидетельствует о том, что количественные данные в Табличке Ковчега – вполне реальные величины.

Исходя из нашего предположения о поперечном сечении веревки (квадрат площадью 1 n2), можно подсчитать и ее общую длину; она равна 31639880n3 /1 п 2 = 31 639 880n, или, в более привычных нам единицах, 527 км. Как уже говорилось в главе 8, это примерно расстояние от Лондона до Эдинбурга!

 

Вавилонские подсчеты

Получив конечный результат Vc, чрезвычайно близкий к сообщенному в табличке Vg, мы, естественно, задаемся вопросом – а как сами вавилоняне могли прийти к этому результату? Ниже мы излагаем наши предположения на этот счет.

Единицу площади 1 ikû они определяли как площадь, равную площади квадратного участка 10 нд  × 10 нд; это давало очень наглядное представление о ее размерах. В поддержку этого приведем слова Энки в Табличке Ковчега:

 

Судно, что ты построишь, нарисуй

На круговом плане!

Пусть будут равны его длина и ширина.

 

Особенно интересно сравнить это распоряжение с табличкой школьных упражнений по геометрии (воспроизведенной и обсуждавшейся в главе 7), на которой изображен круг, вписанный в квадрат.

Производить вычисления, связанные с кругом, вавилонянам было трудно, потому что число π им было известно лишь в очень грубом приближении. Предположим, что для простоты вычислений они представляли себе днище Ковчега площадью в 1 ikû как квадрат со сторонами 10 нд, а стенки – как прямоугольные панели длиной 1 нд и высотой 1 нд. Над всем этим мыслилась еще квадратная крыша, идентичная днищу. Вычислить суммарную площадь всех поверхностей этого тонкого «бисквита» совсем легко; помножив ее затем на толщину плетения, равную 1 пальцу, получаем объем необходимого материала для гипотетического квадратного ковчега – обозначим эту величину Vsq. Подсчеты, тривиальные в этом случае, дают

V sq = 14 400 sūtu.

Эта величина в точности равна 4 šār, и отличается от Vg всего на 0,2 процента!

Дополнительные 30 sūtu, когда их видишь первый раз, кажутся малозначащей и труднообъяснимой деталью. Приведенные выше вычисления, однако, показывают, насколько важна эта деталь: без нее действительно можно было бы предположить, что Ковчег был задуман как квадратное в плане судно. Но эти дополнительные 30 sūtu свидетельствуют против такого предположения.

Тем не менее можно почти с уверенностью утверждать, что для вычислений параметров круглого в плане судна вавилонские писцы использовали «метод квадратуры круга». Мы можем убедиться в этом, вычисляя объем пальмовой веревки для изготовления судна цилиндрической формы, т. е. имеющего круглое днище и вертикальные стенки. Поскольку круг имеет наименьший периметр среди всех фигур с заданной площадью, площадь стенок такого цилиндра будет меньше, чем у стенок судна с квадратным днищем, а его суммарная площадь окажется меньше, чем указанное выше значение Vsq, примерно на 2 %. Как мы видели при собственном расчете Vc, увеличение площади стенок ввиду их выпуклого профиля отчасти компенсирует эти недостающие 2 процента; возможно, вавилоняне эмпирически учитывали этот факт и выработали правило типа «посчитай объем судна, квадратного в плане, и накинь сверху еще немного».

Мы полагаем, что 30 sūtu, добавленные к 4 šār в Vg – это и есть «еще немного». Независимо от того, действительно ли месопотамские корабелы рассчитывали свои суда именно таким способом, легко можно себе представить, как его применяли писцы в рутинных задачах подсчета количества веревки и битума, нужного для постройки судна конкретного типа.

Разумеется, тут же встает следующий вопрос – как они вычисляли это «еще немного» в каждом конкретном случае? Для Ковчега это было 30 sūtu, и естественно предположить, что эта цифра – просто-напросто тридцатикратное увеличение некоей количественной добавки в 1 sūtu, применявшейся для обычных гуфф. Можно развить эту идею дальше, применив использованный выше метод вычислений, но теперь для гуффы диаметром в одну тридцатую диаметра Ковчега. Диаметр такого судна будет равен

4062 п / 30 = 135,4 п,

т. е. немногим более двух метров. Стенки (борта) Ковчега уменьшатся не в той же пропорции, поскольку их высота должна соответствовать практическому использованию судна; в этом можно убедиться, сравнивая реальные гуффы разных размеров. Для гипотетической квадратной гуффы размером в 1/30 Ковчега длина стенки вдоль каждой стороны будет равна 10 нд / 30 = 120 п. Можно выяснить, при какой высоте стенок мы получим разницу («еще немного») в 1 sūtu между круглой гуффой и ее квадратной аппроксимацией, и решить – будет ли гуффа с такой высотой бортов практически пригодной.

Вычисления, которых мы здесь не будем воспроизводить, показывают, что искомая высота равна 34,4 п, т. е. примерно 58 см. Иначе говоря, наш мини-ковчег будет иметь стенки высотой в V своего диаметра. Чтобы переправлять через тихую реку грузы и пассажиров, судно таких пропорций представляется достаточно надежным и практичным. На старинных фотографиях мы видим традиционные гуффы примерно таких пропорций.

Энки, однако, обратился к Атрахасису с очень простой речью – построить судно «размером с поле»[197], и непохоже, что при этом имелась в виду обычная гуффа, увеличенная в 30 раз в диаметре, т. е. с площадью днища в 302 = 900 раз больше. Но в представлении писцов, возможно, учитывался лишь этот коэффициент «30». Известно, что суда той эпохи делались нескольких стандартных размеров в зависимости от требуемого водоизмещения; поэтому вполне естественно могла возникнуть идея вывести некоторые параметры Ковчега экстраполяцией соответствующих параметров стандартного судна диаметром в тридцать раз меньше [198][146].