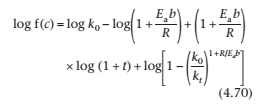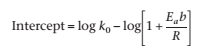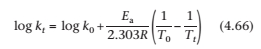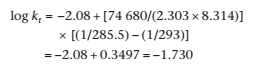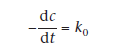В качестве примера мы рассмотрим гидролиз мециллинама (XII), активную против микробов амидопенициллиновую кислоту. Это амфотерное вещество может существовать в виде катиона, который мы можем записать как MH2+, как цвиттер-ион MH±или как анион M-. График 4.10 отражает характеристику степени pH при нулевой концентрации буфера. График сложен тк каждая частица, представленная в растворе, может подвергаться специфическому кислотно-основному катализу в разной степени и таким образом каждая вносит свой вклад в график, изображенный на рисунке 4.10.
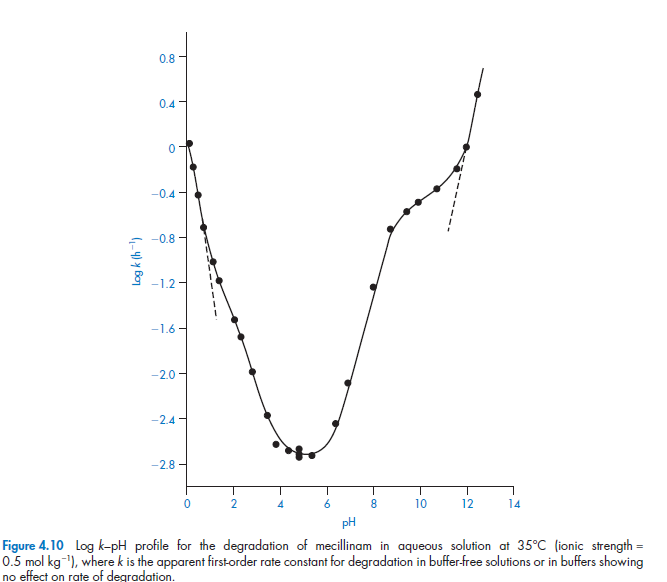

(Часть профиля изменения рН при очень низком значении (ниже 1.2) даётся полностью в результате реакции 1. Это происходит потому, что мециллинам существует в виде катиона МН2, гидролиз которого будет происходить при кислотном катализе в этом диапазоне рН. Плечо в профиле изменения рН при рН2 примерно совпадает с первым значением рКа мециллинама и указывает на кислотный катализ цвиттер-частиц. Снижение константы скорости гидролиза с увеличением рН до 4 можно объяснить, если предположить, что происходят обе реакции 1 и 2. Как видно из рисунка 4.10, скорость гидролиза практически постоянна между рН 4 и 6, это наводит на мысль, что гидролиз происходит при водном катализе (реакция 3) в этой области рН. Скорость гидролиза теперь начинает увеличиваться с ростом рН, это указывает на то, что основный катализ является доминирующим фактором в данном случае. Между рН 6,5 и рКа для ионизации амидина боковых цепей (рКа=8,79) это реакция 4, которая описывает скорость гидролиза. График изменяет наклон при рН 8, поскольку он зависит от изменений, которые происходят в состоянии ионизации амидина боковой цепи. При рН выше 12 мециллинам существует в растворе в виде аниона и это заключение описывается исключительно за счёт базового катализа (реакция 5)
Температура (уравнение аррениуса)
Повышение температуры обычно вызывает очень выраженное повышение скорости гидролиза препаратов в растворе. Если препарат дб стерилизован в клин тестировании используется температура более обычных 80С
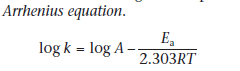
Е- энергия активации, то есть энергетический барьер, который должен быть преодолён, если реакция будет происходить при сталкивание двух реагирующих молекул. А- фактор частоты, который не зависит от температуры данной реакции. R-газовая постоянная (8,314Дж/моль*К) и Т- температура в Кельвинах.
график зависимости logkскорости от 1/Т должен быть линейным с градиентом -Еa/2,303R. Следовательно, предполагая, что порядок реакции не изменяется при изменении температуры, мы можем экстраполировать значения log k относительно 1/t к любому необходимому значению температуры и, таким образом, определить интенсивность распада при этой температурe.
Ионные силы
Уравнение, которое описывает влияние электролита на константу скорости,
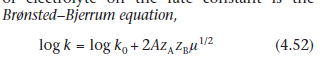
строго справедливо только для ионной силы менее 0,01 моль кг! 01.
В этом уравнении zA и zB - числа зарядов двух взаимодействующих ионов, а A - постоянная для данного растворителя и температуры. Μ - ионная сила раствора, которую мы можем вычислить из
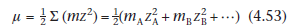
Если ион лекарства и ион электролита являются одновалентными, то ионная сила будет равна общей моляльности раствора. Из уравнения (4.52) видно, что если мы определим константу скорости реакции в присутствии ряда различных концентраций одного и того же электролита, и графика log k против μ1/2, то график должен быть линейным с отрезком прямой log k0 и градиент 2A zA ZB. Это часто встречается даже в растворах с высокой ионной силой, хотя уравнение (4.52)
При более высоких ионных силах (до 0,1 моль кг01) предпочтительно использовать модифицированную форму уравнения Бренстеда- Бьеррума, в котором мы строим log k против μ 1/2(1+ μ 1/2):
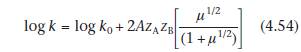
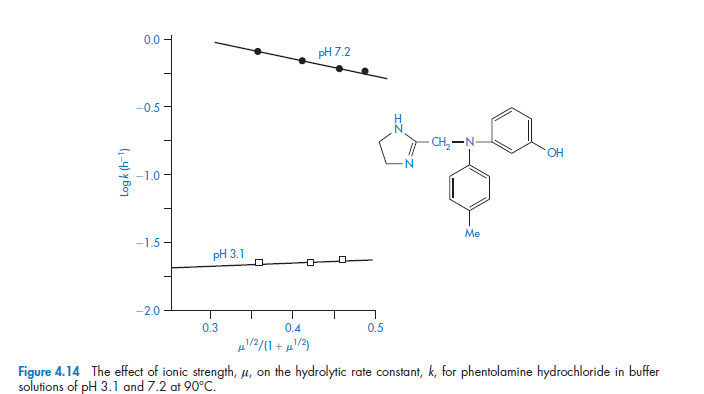
Градиенты этих графиков должны быть пропорциональны произведению заряда, переносимого реагирующими видами. Является ли градиент положительным или отрицательным, зависит от реакции. Реакции между ионами аналогичного заряда, например, катализируемый кислотой гидролиз(Н+) катионного иона-лекарственного средства(К+), приведут к появлению графиков положительного наклона (т.е. скорость реакции будет увеличена путем добавления электролита), тогда как катализируемый основанием гидролиз(ОН-) положительно заряженных(К+) видов лекарств приведет к отрицательным градиентам. Поэтому исследования влияния ионной силы на скорость реакции могут быть использованы для подтверждения типа реакции, которая происходит. Например, градиенты двух графиков рис. 4.14 составляют 0,260 и 01,759 при рН 3,1 и 7,2 соответственно. Так как значение 2A при 90 ° C равно 1,174, мы можем рассчитать значения продукта zA ZB как 0,221 и 1,498 при рН 3,1 и 7,2 соответственно. Эти значения не являются целыми, как они должны быть, если речь идет о реакциях, связанных с кислотой и катализируемой основанием. Это объясняется предположением сложных реакций между буферными веществами и фентоламином при каждом рН.
Пример 4.7 Расчеты с использованием уравнения Бренстеда-Бьеррума Указанные значения константы скорости реакции k при 60 °C для реакции гидролиза пенициллина в фосфатном буфере при pH равном 8.8 в нескольких растворах с различной ионной силой, μ:
k (ч−1) 0.078 0.068 0.056 0.049
μ (моль.кг-1) 0.49 0.38 0.27 0.20
Согласно модифицированному уравнению Бренстеда-Бьеррума (уравнение 4.54) постройте график и определите его тангенс угла наклона. Определите, в котором из этих значений наиболее вероятен кислотный катализ протонированного пенициллин-иона. (Примечание: Значение единицы для данной температуры принять за А.)
Ответ
Тангенс угла наклона графика log k как функции от μ 1/2(1+ μ 1/2) равен + 2.0. Как и ожидалось для реакции между ионами с одноименными зарядами (кислота и протонированный пенициллин-ион), тангенс угла наклона положителен.
Эффекты растворителей
Возможна замена воды в системе на другой растворитель, такой как спирт или пропиленгликоль, Но это эффективн только в определенных системах, в остальных может увеличить скорость разрушения ЛВ.
Уравнение предсказать влияние растворителя на скорость гидролиза, это
log k = log i = ∞  (4.55)
(4.55)
K – константа для данной системы при данной температуре. Мы можем увидеть, что график log k как обратная функция от диэлектрической константы растворителя, ε, должен быть линейным с градиентом величины 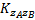 и угловым коэффициентом, равными логарифму константы скорости в идеальном растворителе с бесконечной диэлектрической константой.
и угловым коэффициентом, равными логарифму константы скорости в идеальном растворителе с бесконечной диэлектрической константой.
Если заряды ионов лекарственного вещества и взаимодействующего с ним соединения будут одинаковы, то тогда мы увидим, что тангенс угла наклона графика будет отрицательным. В этом случае, если мы заменим воду на растворитель с меньшей диэлектрической константой, тогда мы добьемся желаемого эффекта снижения скорости реакции.
Если же заряды ионов лекарственного вещества и взаимодействующего с ним соединения противоположны, то в этом случае тангенс угла наклона будет положительный и выбор неполярного растворителя только усилит распад.
Свет – Фотораспад(изомеризация всякая). Фоточувствтельные хранят в флаконах из Янтарное стекло отчасти эффективно в этом плане, так как не пропускает свет с длинной волны менее 470 нм. В качестве превентивной меры, рекомендуется хранить фотолабильные лекарственные средства в защищенном от света месте.
Фотодегидратация нескольких препаратов также зависит от рН.Так, например, фотохимическое разложение бензодиазепина мидазолама Xlll возрастает с ростом рН ^15 и ципрофлоксацин XlV является наиболее чувствительным к фотодегидратации в цвиттер-ионной форме, стабильность увеличиваться, когда рН снижается до 3-4^16
Кислород– выдерживают при испытаниях в капсуле с кислородом. Если оч чувствительно стараются заменит О2 на N2 или CO2. Исключают контакт с тяж Ме (катализаторы), антиоксиданты
Следует также отметить, что окислительное разложение некоторых препаратов в растворе может зависеть от рН, например, окисление преднизолона при основном катализе. Аналогичным образом, окисление морфина происходит более быстро в щелочном или нейтральном растворе, чем в кислом. Причиной этого может быть влияние рН на окислительно-восстановительный потенциал Е0 препарата.
ПАВ
Неполярные соединения, как принято полагать, встраиваются в липофильное ядро мицеллы и, в силу этого, вероятно, более эффективно изолированы от влияния воздействующих веществ, нежели те соединения, которые расположены ближе к поверхности мицеллы.
При гидролизе, катализируемом основаниями, солюбилизация в анионные мицеллы позволяет стабилизировать лекарственное вещество, так как поверхность мицелл отталкивает ОН--ионы. Напротив, солюбилизация в катионных мицеллах вызовет усиление гидролиза, катализируемого основаниями.
Многие лекарственные вещества способны формировать мицеллы в водных растворах (см. раздел 6.3) и некоторые исследования сообщали о влиянии подобной самоассоциации на стабильность. В мицеллярных расвторах бензилпенициллина (500 000 ед/см-3) кажущаяся скорость распада, катализируемого Н+-ионом, возросла в два раза, а кажущаяся скорость распада, катализируемого водой и ОН--ионами, снизилась в 2-3 раза.17 Впоследствии, уровень pH сместился в сторону более высоких значений, а также было выявлено, что значение рН минимального уровня гидролиза равно 7.0, в сравнении с 6.5 для мономерного раствора (8000 ед/см-3). В сравнении с рН-профилем минимумов, мицеллярный бензилпенициллин оказался в 2.5 стабильнее, чем в мономерном состоянии, в условиях неизменного уровня рН и ионной силы.
Степень влияния зависит от разницы констант скоростей реакции, когда лекарственное вещество находится в водном растворе и в мицеллярной форме, а также от степени солюбилизации. Таким образом,
kobs = kmfm + kwfw (4.56)
где kobs, km и kw - исследуемая, водная и мицеллярная константы скорости, соответственно, а fm и fw – доли лекарственного вещества в мицеллах и в водной фазе, соответственно. Значение km зависит от расположения лекарственного вещества в мицелле.
4.4.2 Мягкие лекарственные формы (полутвердые…)
Химическая стабильность лекарственных веществ, входящих в состав мазей или кремов, часто зависит от природы, использующейся в них основы. Гидрокортизон в ряде доступных в продаже препаратов показывает максимальную нестабильность в основах из полиэтиленгликоля. Заявленный срок годности составлял всего 6 месяцев, что делало коммерческое производство невыгодным, учитывая количество времени, необходимое на путь препарата от производителя к пациенту.
При выборе основы для мази проблему стабильности лекарственного следует иметь в виду не только вещества на этапе разработки состава лекарственного препарата, но и на более поздних этапах, если данная мазь будет подвергаться разбавлению. Разбавление, к сожалению, является распространенной практикой в случае, если лечащий врач хочет снизить активность сильнодействующих препаратов для местного нанесения, в частности, стероидов. Фармацевтические и биофармацевтические риски такой процедуры неоднократно обсуждались.20 Особый интерес представляет проблема стабильности лекарственного вещества в случае использования неподходящих разбавителей. Приведенным примером является разбавление крема с бетаметазона валератом основой, имеющей рН от нейтрального к слабощелочному. В таких условиях возможно перемещение остатка валериановой кислоты из 17 в 21 положение, что приводит к образованию менее активной формы бетаметазона валерата. Аналогичным образом разбавители, содержащие окислители, могут вызывать разрушение флуоцинолона ацетонида до менее активных соединений.
Включение лекарственного вещества в гелеобразные структуры зачастую ведет к изменению его стабильности, к примеру, усиление распада бензилпенициллина натрия в гидрогелях из различных природных и полусинтетических полимеров. При значении рН, равном 6, в карбополовых гидрогелях процентное содержание неразложившегося пилокарпина в равновесии является простой функцией от кажущейся вязкости среды. Изменения вязкости, тем не менее, не сильно затрагивали константа скорости разложения. Было установлено незначительное влияние вязкости на скорость окисления аскорбиновой кислоты в растворах гелей полисорбата 80
Твердые ЛВ
Влага
● В твердых лекарственных формах, содержащих лекарственные средства, чувствительные к гидролизу, разложение лекарственного средства может происходить, если влаге адсорбируется на поверхности лекарственной формы. В таких случаях стоит стараться приготовить менее гигроскопичную соль лекарственного вещества. Тщательный отбор упаковки также важен. На лекарственное средство, которое растворяется в этом поверхностном слое, будут влиять многие факторы, которые влияют на разложение лекарств в водном растворе.
Вспомогательные вва
Вспомогательные вещества твердой лекарственной формы могут влиять на распад препарата увеличивая содержания влаги в лекарственной форме.Однако сила их влияния зависит от того, насколько сильно он связан с лекарственным веществом, и то, насколько сильно влага вступает в контакт с лекарственным веществом.
(крахмал и повидон - равновесное влагосодержание повидона составляет около 28% при 75% относительной влажности воздуха; Трисиликат магния вызывает усиление гидролиза аспирина в таблетках, так как считается, что данное лекарство содержит большое количество влаги.)
Замена феноцетина в соединении кодеина и в таблетках аспирина на парацетамол NHS препаратов в Австралии в 1960-х (из-за нежелательных побочных эффектов, вызванных феноцетином) привела к снижению стабильности таблеток данных препаратов. Позднее причина была обусловлена реакцией трансацетилирования между аспирином и парацетамолом, а также возможным прямым гидролизом парацетамола
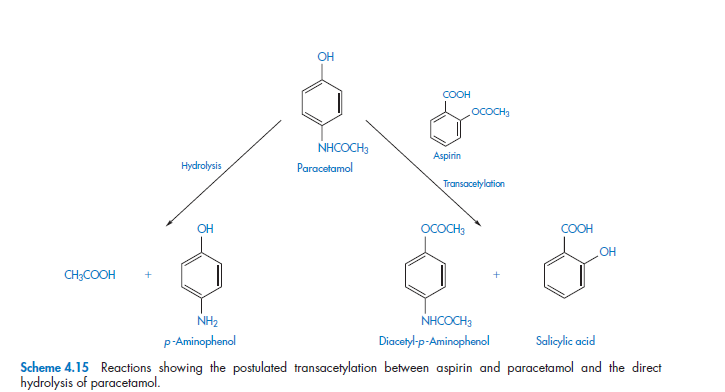
Добавление 1% талька вызывает незначительное повышение расщепления, когда как добавление 0.5% магния стеарата существенно увеличивает скорость распада.
Расщепляющий эффект (индуцируют) щелочной гидролиз щелочных стеаратов (примененяются данные соли в качестве смазочных агентов при производстве таблеток) ингибируется в присутствии яблочной, циклогексилсульфаминовой или малеиновой кислот, вследствие, как предполагается, конкуренции между лекарственным веществом и добавленной кислотой за катион смазочного агента.
Основа, которая используется при разработке суппозиториев, часто может влиять на интенсивность расщепления действующих веществ. Аспирин разлагается на несколько полиэтиленгликолей, которые входят в состав основ для суппозиториев. Было показано, что расщепление частично обусловлено переэтерификацией, продуктами которой являются салициловая кислота и ацетилированный полиэтиленгликоль. Интенсивность распада, которая описывается кинетической реакцией псевдопервого порядка значительно выше, чем когда была использована жирная основа, такая как кокосовое масло.
Могут оказать влияние на светостойкость продукта
свободно радикальные реакции с участием фенольных примесей в таблетках, такими как кросповидон и вязкость-модифицирующие агенты, такие как альгинаты, могут привести к фотодеградация. Аналогичным образом окрашенные продукты могут быть образованы по реакции альдегидов, образующихся в процессе сушки, распылением или автоклавированием лактозы с первичными аминогруппами в продукте.
Температура
● Повышение температуры приводит к увеличению скорости распада препаратов в твердой дозировке. Препарат или один из вспомогательных веществ может, например, расплавиться или изменить свою полиморфную форму, при увеличении температуры, или он может содержать свободные связи с водой, которая теряется при более высоких температурах.
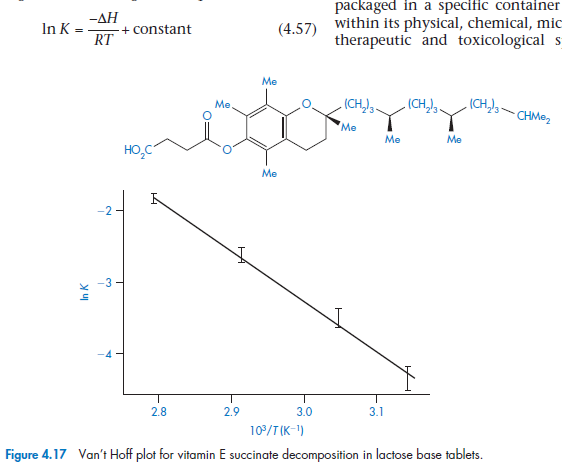
Может быть описаны уравнением Аррениуса(т.е. отношение logk к 1/T являются линейным.), хотя эффект изменения температуры обычно намного сложнее, чем для жидких ЛВ. Это уравнение не может быть использовано для систем, которые близки кравновесию(витамин А в желатиновых гранулах и витамина Е в лактозе таблеток), для них – можно Уравнение Ван-Гоффа (его здесь обозвали Хоффом)
Свет и кислород
Фотораспад, и окисление. Во влаге тоже есть кислород – следует учитывать
17. Стабильность лекарственных веществ. Тестирование стабильности и прогнозирование сохраняемости. Влияние температуры на стабильность. Другие факторы окружающей среды, влияющие на стабильность. Протокол тестирования стабильности.
Тестирование и прогнозирование срока годности. Стабильность
Самое важное - иметь гарантии, что конкретный состав при упаковке в конкретном контейнере будет оставаться в пределах своих физических, химических, микробиологических лечебных и токсикологических спецификаций и что будет нормальный доступ кислорода во время хранения на указанное время
Для того, чтобы сделать такую гарантию, очевидно, что нам следует провести тщательные испытания стабильности продукта в той форме, в которой она в итоге пойдёт на рынок. Так как срок испытаний может длиться около двух лет, то старались разработать ускоренные методы – повышение температуры
Остальные – естественные- испытания вроде микробиолгич чистоты опущены
Влияние температуры на стабильность
Мы уже рассматривали базовые методы ускорения химического разложения препаратов путём повышения температуры. Мы кратко пересмотрим естественные стадии в этом процессе. Порядок реакции может быть определен путём построения графика стабильности при нескольких значениях повышенных температур, в соответствии с уравнениями, описывающими зависимость распада вещества от времени для всех порядков реакции, пока линейный график не будет получен. Таким образом, мы можем рассчитать значения констант скорости при любой температуре, основываясь на наклоне этих графиков и графика в координатах logk – t (температура), в соответствии с уравнением Аррениуса:
Log k = log A – (Ea/2,303RT) (4.58)
Требуемое значение k может быть подставлено из этого графика при комнатной температуре, а энергия активации Ea может быть рассчитана из выражения –Ea/2,303R. Значение Ea обычно находится в пределах интервала 50-96 кДж*моль^-1.
Удобный, приблизительный метод, который полезен для определения скорости распада при комнатной температуре применяется в соотношении констант скорости при комнатной температуре (Т1) и повышенной температуры (Т2). Если в уравнение Аррениуса подставить Т1 и из полученного результата вычесть результат, полученный при Т2, то мы получим:
Log(k2/k1)=-Ea/2.303R(1/T2-1/T1) (4.59)
Или
Log(k2/k1)=Ea(T2-T1)/2.303RT2T1 (4.60)
Конечно, нам необходимо значение Еа для того, чтобы было возможно использовать эти уравнения для расчета константы скорости k1 при комнатной температуре. Если нам нужно лишь приблизительное значение k1, то принять ее за половину от значения Еа, допустим 75кДж*моль-1
Пример 4.8 Применение уравнения Аррениуса.
Константа скорости для реакции первого порядка, гидролиза сульфацетамида при 120С равна 9*10^-6 c^-1, а энергия активации равна 94кДж*моль^-1. Рассчитайте константу скорости при 25С.
Ответ
Используя уравнение 4.60 со значением Еа 94кДж*моль^-1, мы получаем:
Log(k120/k25)=94*10^3*(393-298)/2.303*8.314*(393*298)=3.98
Убираем логарифмы,k120/k25=9.55*10^3. Из этого следует, k25=9*10^-6/9.55*10^3=9.4*10^-10 c^-1.
Альтернативный метод использования данных – построение графика в координатах logt0.5-T, где t0.5 –период полураспада, а Т – температура. Из уравнения 4.13 следует, что t0.5=0,639/k. отсюда следует:
Logk=log0.639-logt0.5 (4.61)
Подставляем в уравнение 4.51 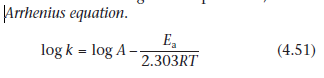 и получаем:
и получаем:
Logt0.5=log0.693-logA+(Ea/2.303RT) (4.62)
После того, как мы рассчитали константу скорости для требуемой температуры хранения, нетрудно высчитать срок годности продукта, основанный на приемлемой степени разложения. Уравнение, которое мы можем использовать для расчета потери активности на 10% может быть получено путем подстановки выражения х=0.1а в уравнения нулевого и первого порядков (уравнение 4.8; 4.10), получаем:
t0.9=0.1[D]0/k0 (нулевой порядок) (4.63)
и
t0.9=0.105/k1 (первый порядок) (4.64)
Где [D]0 – начальная концентрация лекарственного средства. Несмотря на то, что t0.9 обычно используется для установления срока годности, другая степень разложения может потребоваться, например, когда разложение лекарств приводит к изменению цвета или нежелательным побочным эффектам. Используемые в таких случаях уравнения могут быть выведены подставкой в соответствующие уравнения скорости.
Пример 4.9. Расчет срока годности
Начальная концентрация активного вещества в водном препарате была 5*10^-3г*см^-3. После 20 месяцев анализ показал, что концентрация равна 4.8 г*см^-3. Известно, что лекарственное средство перестает быть эффективным после разложения до 70% от ее начальной концентрации. Принимая во внимание то, что разложение проходит по правилам кинетики для реакций первого порядка, рассчитайте конец срока годности препарата.
Ответ
Подставляем в уравнение для реакций первого порядка (уравнение 4.10)
K=(2.303/20)[(log5*10^-3)/(4.2*10^-3)]
K=8.719*10^-3 месяц^-1
70% от начальной концентрации равны 3.5*10^-3 г*см^-3.
t=(2.303/8.719*10^-3)*[(log5*10^-3)/(3.5*10^-3)]
T=40.9 месяцев
Отсюда следует, что срок годности составляет 40.9 месяцев.
Хотя экспресс тест, основанный на уравнении Аррениуса значительно сокращает затраты времени, все равно он включает в себя шаг, требующий временных затрат, а именно – определение порядка реакции разложения. Когда большинство исследователей делали акцент на необходимости знания определенного кинетического пути распада, некоторые пропускали этот начальный шаг, принимая во внимание определенную модель распада. При менее чем 10%ном разложении, и в пределах экспериментальной ошибки, включенной в стабильность опытов, невозможно найти различия между кинетикой реакций нулевого, первого или простыми реакциями второго порядка, используя метод построения кривой; следовательно, чтобы присвоить любой реакции распада первый порядок, необходимо убедиться в том, что погрешность минимальна. Было доказано, что существует линейная зависимость, между логарифмом от t0,9 (время, затраченное на разложение до 90% от начальной концентрации вещества) и температурой, которая не зависит от порядка реакции разложения некоторых лекарств. В основе этих открытий, было предложено использование таких линейных графиков для расчета t0,9 при запрашиваемой температуре, что обеспечивает быстроту, и в то же время достаточную точность исследования скорости распада на стадии разработки.
Даже с модификациями, предложенными выше, метод тестирования стабильности, основанный на уравнении Аррениуса, остаётся наиболее быстрым, принимая во внимание то, что он предполагает отдельный расчет констант скорости для различных температур. Разработанные экспериментальные методики облегчают расчет скорости распада при единичном эксперименте. Эти методы включают повышение температуры ЛС, в соответствии с уже рассчитанной программой режимом температура/время и, следовательно, упоминается как исследование неизотермальной стабильности.
Может быть использован любой подходящий режим температура/время В методе Роджерса, повышение температуры было запрограммированно так, что значение обратное температуре изменялось логарифмически со временем в соответствие с выражением,
 Где T0 и T– это температура в нулевой момент времени и в момент времени t, соответственно, и b– коэффициент пропорциональности. Применение уравнения Аррениуса к двум значениям температур и вычитание дает
Где T0 и T– это температура в нулевой момент времени и в момент времени t, соответственно, и b– коэффициент пропорциональности. Применение уравнения Аррениуса к двум значениям температур и вычитание дает

Подставляя уравнение (4.65) в уравнение (4.66) получаем
 Следовательно,
Следовательно,
 Для реакции первого порядка -dc/dt=kc, где с – концентрация. Подставляя kиз уравнения (4.68) и объединяя, получаем
Для реакции первого порядка -dc/dt=kc, где с – концентрация. Подставляя kиз уравнения (4.68) и объединяя, получаем
 Где c0и ctконцентрации в нулевой момент времени и момент времени t, соответственно.
Где c0и ctконцентрации в нулевой момент времени и момент времени t, соответственно.
Следовательно,

Похожее уравнение относится к реакциям второго порядка

Где a0и b0 -концентрации в начале эксперимента, и atи bt – концентрации в момент времени t. Значение конечного члена уравнения (4.70) стремится у нулю при kt, становясь больше k0. Таким образом график logf(c) против lof (1+t) будет линейным с того времени, как k0 станет очень мала по сравнению с kt, и ею можно будет пренебречь. Наклон линии - это (1 + bEa/R), позволяет определить Ea. Константа скорости k0 может быть посчитана в перехвате, где log(1 + t)=0, что эквивалентно logk0 – log(1 + bEa/R). Константа скорости при любой другой температуре может быть посчитана из k0и Ea.
Задача 3.10 Ускоренное тестирование хранения с использованием программы температуры во времени
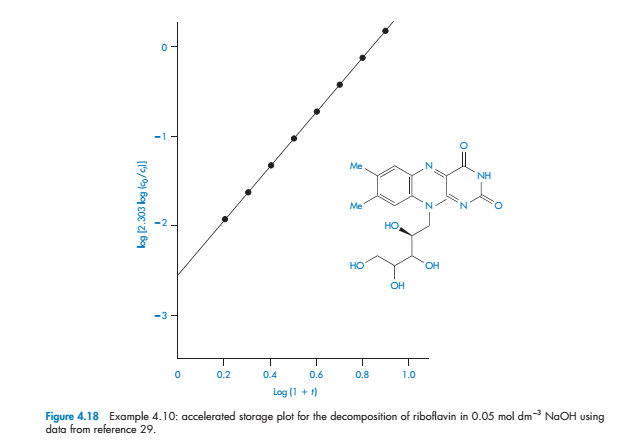
При изучении разложения первого порядка рибофлавина в 0,05 моль дм-3 NaOH с использованием ускоренных методов хранения, температура была запрограммирована подняться от 12,5 до 55 °С с использованием программной константы, b, 2,171 x 10-4 K-1. Начальная концентрация, c0, рибофлавина была 10-4 моль дм-3, а концентрация ct во времени t была следующей:

Вычислите энергию активации и константы скорости при температуре 20 °С.
Ответ:
Для реакций первого порядка данные приведены в соответствии с уравнениями (4.70) и (4.71).
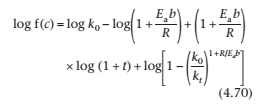


График log[2,303 log(c0/ct)] против log(1 + T) является линейным (см. рис. 4.18) с наклоном 2,95.
Из уравнения (4.70),

Наклон = 1 + Eab/R;
Следовательно,
Ea = (1,95 × 8,314) / (2,171 × 10-4) = = 74,68 кДж моль-1
Перехват при log(1 + t) = 0 равняется -2,55. Из уравнения (4.70),
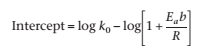
где последним членом в правой части уравнения (4.70) можно пренебречь.
Следовательно,
log k0 = −2,55 + log 2,95 = −2,08
k0 = 0,0083 ч-1
То есть, константа скорости при температуре T0 (12,5 °С) составляет 0,0083 ч-1.
Константа скорости при 20 °C может быть вычислена из уравнения Аррениуса в форме уравнения (4.66):
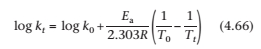
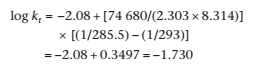
kt = 1,86 × 10−2 ч−1
Константа скорости при 20 °C, таким образом, равняется 0,0186 ч-1.
Преимущества данного метода над обычным методом испытании стабильности заключается в том, что (a) данные, необходимые для расчета устойчивости получены в одном однодневном эксперименте, а не из серии экспериментов, которые могут длиться несколько недель; (b) не требуется никаких предварительных экспериментов, чтобы определить оптимальную температуру для определения ускоренного старения; и (с) линейность графика logf(c) по сравнению с log(1+t) подтверждает, что был предположен правильный порядок реакции.
Были предложены ряд улучшений базовых методов неизотермических испытаний на стабильность. Вместо того, чтобы подвергать лекарственную форму предварительному фиксированию соотношения температуры ко времени, температура может изменяться в течение испытаний со скоростью, соответсвующей аналитическим результатам эксперимента. Зависимость время-температура подставляется в полиномное выражение достаточной для описания изменений степени. Это соотношение и экспериментальные данные после комбинируются и используются для вычислений путей биодеградаций, соответсвующих сериям значений энергии активации. Кривые совмещаются с экспериментальными данными для получения корректных значений энергии активации для данной реакции. Используя эту энергию активации и аналитические данные можно подсчитать скорость и реакции и определить стабильность вещества. Вычислительные процедуры, с помощью которых можно определить энергию активации и частотный фактор уравнения Аррениуса, используя простые неизометрические эксперименты с заданной зависимостью температуры от времени были описаны ранее.
Так же было предложено улучшение модели испытаний на стабильность, которое помогает избежать сложностей, присущих методу подбора нелинейных кривых.Должен быть проведен эксперимент, при котором изменение температуры образца проводится до деградации, достаточно быстрой, чтобы принять ее как проходящую при изотермических условиях. Аналитическая информация, полученная в результате неизометмической и изотермической составляющих эксперимента, используется в расчетах энергии активации и при определении порядка и скорости реакции, а также для предсказания стабильности при любой заданной температуре. Очевидно, что для увеличения срока годности препарата, необходимо обеспечить стабильность лекарственных форм, но при этом очень важно не забывать о существующих ограничениях применяемых для этого методик. Мы должны убедиться, что порядок реации при высоких температурах не отличается от порядка реакций, проходящих при комнатной температуре, как, например, при деградации комплексных соединений, где вовлечены параллельные или последовательные реакции. Здесь возможны изменения в соотношении участников реакции при увеличении температуры.
Суспензии
Сложность, возникающая при проведении испытаний на стабильность суспензий, заключается в изменение растворимости вещества с увеличением температуры. В суспензиях концентрация лекарственного препарата в растворе обычно сохраняется постоянной, так как большая часть вещества растворятся для сохранения насыщенного состояния раствора. Данная ситуация обычно присуща кинетике реакций нулевого порядка. Фактически разложение растворенного вещества является реакцией первого порядка, в таком случае мы можем выразить уменьшение концентрации, с, со временем, t, как
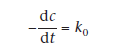
где k0=kaS и S — это расстовримость лекарственного препарата.
Проблема данной системы заключаетмя в том, что при увеличении температуры увеличивается не только константа скорости реакции, но так же и константа растворимости. Уравниение Аррениуса должно включать данные об изменений растворимости вещества относительно использованного диапазона температур. Альтенативный метод, который не требует измерения растворимости, использует отношение между растворимостью и температурой:

где дельта Hf — это молярная теплота плавления. Теперь мы можем сопоставить log k0 и 1/T и экстраполировать для получения значений k 0 при комнатной температуре. Очень важно помнить, что для большего терапевтического эффекта, превращения препарата в растворе следует по законам кинетики уравнений первого порядка, и что скорость не лимитирована скоростью растворения.
Твердое состояние
Основные проблемы, возникающие при измерении стабильности твердых лекарственных форм:
а) аналитические результаты склонны иметь более разбросанный характер, так как таблетки и капсулы являются дозированными единицами, не эквивалентными стехиометрическим коэффициентам, встречаемым в учениях о стабильности веществ в растворах
б) эти лекарственные формы являются гетерогенными системами, часто включающими газовую фазу (воздух и водяной пар), жидкую фазу (поглощенную влагу) и саму твердую фазу. Соотношение этих фаз может варьировать в течение эксперимента.
Первую трудность можно избежать, обеспечивая равномерность лекарственной формы до исследования стабильности. Проблема гетерогенности более трудна для преодоления. Наибольшая сложность связана с наличием поглощенной влаги. В разделе 4.4.3 мы показали, что поглощенная влага может оказывать значительный эффект на кинетику разложения и это может осложнить проведение испытаний на стабильность. Можно привести в пример желатиновые капсулы, в которых содержание воды в оболочке капсулы должно уравновеситься с водой, содержащейся в лекарственном препарате и в окружающем воздухе. Это может занять значительное количество времени. Так же осложнено испытание стабильности лекарственных форм, в которых происходит химическое взаимодействие между компонентами вещества, другими словами система находится в химическом равновесии. На практике, данные о стабильности вещества, чаще отображают на графике в соответствие с уравнением Вант-Гоффа, чем используя уравнение Аррениуса.
Чтобы уменьшить значимость этих проблем, в частности связанных с поглощенной влагой, в течение испытаний стабильности,было предложено следующее24:
а) использование плотно запечатанных контейнеров, за исключением случаев, когда должно быть исследовано влияние упаковки
б) содержание воды, присутствующее в лекарственной форме должно быть определено, предпочтительно при всех температурах хранения
в) разделенные, укупоренные ампулы должны тестироваться индивидуально, избегая таким образом избегая изменения содержания воды от открытия контейнера.
Как было описано выше, мы можем испльзовать уравнение Аррениуса для предсказания стабильности вещества в твердом состоянии, не смотря на то, что кинетика распада отличается от таковой в растворе. Исключением являются равновесные реации, в которые лучше пользоваться уравнением Вант-Гоффа (уравнение 4.57) для предсказания стабильности при комнатной температуре.
Другие факторы окружающей среды, влияющие на стабильность
Свет
Испытание фотостабильности лекарственных веществ обычно начинаются с первичного стресс-тестирования для определения его фотостабильности в целом и идентификации любых продуктов деградации. В этом процессе образцы облучаются при всех длинах волн, используя световой ресурс широкого спектра. Те препараты или лекарственные формы, которые проявили фоточувствительность, после отбираются для более тщательного испытания, в котором они облучаются светом той длиной волны, с которой будут сталкиваться во время хранения и использования. В течение срока годности наиболее вероятно, что продукты будут подвергаться флуоресцентному излучению, прямым солнечным лучам и солнечным лучам, прошедшим через стекло, таким образом испытание на стабильность должно быть организовано так, чтобы покрыть эти возможные варианты. Специальный протокол испытаний на фотостабильность новых лекарственных препаратов и их продуктов описан в ICHGUILDLINE.
Кислород
Стабильность лекарственных веществ, проявляющих восстановительные свойства, обычно обусловлена действием антиоксидантов, включенных в лекарственную форму. Влияние кислорода на стабильность может возрастать при увеличении парциального давления кислорода в системе. Проведение испытаний на кислородоустойчивость бывает затруд<







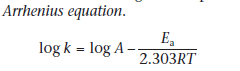
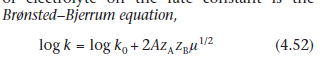
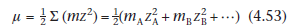
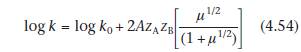

 (4.55)
(4.55)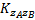 и угловым коэффициентом, равными логарифму константы скорости в идеальном растворителе с бесконечной диэлектрической константой.
и угловым коэффициентом, равными логарифму константы скорости в идеальном растворителе с бесконечной диэлектрической константой.

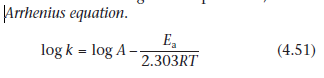 и получаем:
и получаем: Где T0 и T– это температура в нулевой момент времени и в момент времени t, соответственно, и b– коэффициент пропорциональности. Применение уравнения Аррениуса к двум значениям температур и вычитание дает
Где T0 и T– это температура в нулевой момент времени и в момент времени t, соответственно, и b– коэффициент пропорциональности. Применение уравнения Аррениуса к двум значениям температур и вычитание дает