Мольная доля компонента в растворе –это число молей этого компонента, разделенное на общее количество молей, присутствующих в растворе. В двухкомпонентном (бинарном) растворе мольная доля растворителя х1 рассчитывается х1=n1/(n1+n2), где n1 и n2 соответственно число молей в растворителе и в растворенном веществе, присутствующем в растворе. Таким же образом мольная доля растворителя х2 рассчитывается х2=n2/(n1+n2). Сумма мольных долей всех компонентов равна единице, то есть в бинарном растворе х1+х2=1.
Пример 3.1. единицы концентрации
Изотонический раствор содержит 0,9% NaCl (М=58,5). Выразим концентрацию этого раствора как: (а)молярность, (b)моляльность, (с) мольная доля и (d) миллиэквиваленты Na+в литре. Примем, что плотность изотонического раствора равна 1 г*см-3.
Ответ.
(а) 0,9% раствор NaCl содержит 9 г/дм-3= 0,154 моль*дм-3.
(b) 9 г NaCl растворяется в 991 г воды (принятая плотность= 1 г*см-3).
Следовательно, 1000 г воды содержит 9,08 г NaCl = 0,155 моль,то есть моляльность = 0,155 моль*кг-1.
(с) Мольная доля NaCl,х1, рассчитывается:
х1=n1/(n1+n2)=0,154/(0,154+55,6)=2,79*10-3
(991 г воды содержит 991/18 моль,то есть n2=55,06)
(d)Так как Na+ моновалентен, число миллиэквивалентов Na+=числу миллимоль.
Поэтому раствор содержит 154 миллиэквивалентов*дм-3 Na+.
Термодинамика- краткое введение
Важность термодинамики в фармацевтических науках стала явной, когда поняли, что такие процессы как деление на части растворов между несмешивающимися растворителями, растворимость лекарства, образование мицелл и взаимодействие лекарства с рецептором могут быть описаны термодинамическими понятиями.
Энергия
Энергия –это фундаментальный показатель системы. Она определяет какая реакция может произойти, как быстро реакция может произойти и в каком направлении реакция будет происходит. Различают: кинетическая энергия заключается в том, какой тело обладает в результате его движения; потенциальная э нергия – это энергия,которую имеет тело, из-за его положения, будь то потенциальная энергия гравитации или кулоновская потенциальная энергия, которая связана с заряженными частицами. Все формы энергии связаны, но в превращении между различными типами невозможно создать или разрушить энергии. Это закон сохранении энергии - Изменение внутренней энергии системы равно количеству сообщенной системе теплоты минус количество работы, совершенной системой против внешних сил. (первый закон термодинамики)
Внутренняя энергия U системы – это сумма всех кинетических и потенциальных энергетических вкладов в энергию всех атомов, ионов и молекул в этой системе. В термодинамике мы скорее изучаем изменения внутренней энергии, ∆U, чем саму внутреннюю энергию. Мы можем изменять внутреннюю энергию у закрытых систем (она не может обмениваться веществом с ее окружением) только 2 способами: передача энергии в виде работы (w)или в виде тепла (q). Выражение для изменения внутренней энергии:
∆U=w+q
Если система выделяет свою энергию в окружающую среду, то ∆U отрицательная, то есть сумма внутренней энергии была уменьшена. Где тепло поглощается (как в э ндотермическом процессе) внутренняя энергия будет увеличиваться и, следовательно, q будет положительным. Наоборот, в процессе, который выделяет тепло (экзотермический процесс), внутренняя энергия уменьшается и q отрицательное. Таким же образом, когда энергия поставляется в систему в виде работы, w положительная; а когда система теряет энергию при выполнении работы, w отрицательная.
Часто необходимо рассматривать бесконечно малые изменения в показателях; мы обозначаем это использованием d, а не ∆. Так для бесконечно малых изменений во внутренней энергии уравнение:
dU=dw+dq
Из этого уравнения мы можем увидеть, что независимо от того получена была энергия как тепло или работа, или их смесь: изменение внутренней энергии одинаково.
Из уравнения следует, что система, которая полностью изолирована от окружающей среды, так, что не может обмениваться теплом или взаимодействовать механически, чтобы выполнить работу, не может подвергаться никаким изменениям в ее внутренней энергии. Другими словами, внутренняя энергия изолированной системы - постоянна, это первое начало термодинамики.
Невозможен вечный двигатель первого рода (двигатель, совершающий работу без затраты энергии).
ИЗ ХАРИТОШИ
Изменение внутренней энергии системы равно количеству сообщенной системе теплоты минус количество работы, совершенной системой против внешних сил.


Уравнение является математической записью 1-го начала термодинамики для конечного, уравнение 2 – для бесконечно малого изменения состояния системы.
Внутренняя энергия является функцией состояния; это означает, что изменение внутренней энергии ΔU не зависит от пути перехода системы из состояния 1 в состояние 2 и равно разности величин внутренней энергии U2 и U1 в этих состояниях:

Следует отметить, что определить абсолютное значение внутренней энергии системы невозможно; термодинамику интересует лишь изменение внутренней энергии в ходе какого-либо процесса.
Рассмотрим приложение первого начала термодинамики для определения работы, совершаемой системой при различных термодинамических процессах (мы будем рассматривать простейший случай – работу расширения идеального газа).
Изохорный процесс (V = const; ΔV = 0).
Поскольку работа расширения равна произведению давления и изменения объема, для изохорного процесса получаем:
 (I.1)
(I.1)
 (I.4)
(I.4)
 (I.5)
(I.5)
Изотермический процесс (Т = const).
Из уравнения состояния одного моля идеального газа получаем:
 (I.6)
(I.6)
 (I.8)
(I.8)
Изобарный процесс (Р = const).
 (I.9)
(I.9)
Подставляя полученные выражения для работы различных процессов в уравнение (I.1), для тепловых эффектов этих процессов получим:
 (I.10)
(I.10)
 (I.11)
(I.11)
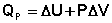 (I.12)
(I.12)
В уравнении (I.12) сгруппируем переменные с одинаковыми индексами. Получаем:
 (I.13)
(I.13)
Введем новую функцию состояния системы – энтальпию H, тождественно равную сумме внутренней энергии и произведения давления на объем:

Тогда выражение (I.13) преобразуется к следующему виду:
 (I.14)
(I.14)
Т.о., тепловой эффект изобарного процесса равен изменению энтальпии системы.
Адиабатический процесс (Q = 0).
При адиабатическом процессе работа расширения совершается за счёт уменьшения внутренней энергии газа:
 (I.15)
(I.15)
В случае если Cv не зависит от температуры (что справедливо для многих реальных газов), работа, произведённая газом при его адиабатическом расширении, прямо пропорциональна разности температур:
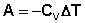 (I.16)
(I.16)
Энтальпия
Когда изменения происходят в системе под действием постоянного давления, например, в химической реакции в открытом сосуде, тогда возрастание внутренней энергии не равно энергии, поступающей в виде тепла, потому что часть энергии будет затрачиваться на работу (против атмосферы) при расширении системы. Это удобно, поэтому рассмотрим тепловые изменения без сопутствующих изменений в работе. По этой причине мы рассмотрим показатель, который равен поступлению тепла под постоянным давлением: этот показатель называется энтальпией (Н). Мы можем определить энтальпию:
∆Н=q под постоянным давлением (3.3)
∆Н положительная, когда тепло поступает в систему, которая свободно может менять свой объем, и отрицательная, когда система выделяет тепло (как в экзотермической реакции). Энтальпия связана с внутренней энергией системы уравнением:
H=U+pV (3.4)
Где p и V соответственно давление и объем системы.
Изменения энтальпии сопутствует таким процессам, как растворение вва, формирование мицелл, химическая реакция, адсорбция на твердых частицах, выпаривание растворителя, гидратация в растворенного вещества, нейтрализация кислот и оснований и плавление или заморозка вва.
ИЗ ХАРИТОШИ
Теплота образования вещества – тепловой эффект реакции образования 1 моля сложного вещества из простых. Теплоты образования простых веществ принимаются равными нулю.
Теплота сгорания вещества – тепловой эффект реакции окисления 1 моля вещества в избытке кислорода до высших устойчивых оксидов.
Теплота растворения – тепловой эффект процесса растворения 1 моля вещества в бесконечно большом количестве растворителя. Теплота растворения складывается из двух составляющих: теплоты разрушения кристаллической решетки (для твердого вещества) и теплоты сольватации:


Поскольку ΔНкр.реш всегда положительно (на разрушение кристаллической решетки необходимо затратить энергию), а ΔНсольв всегда отрицательно, знак ΔНраств определяется соотношением абсолютных величин ΔНкр.реш и ΔНсольв:
Основным законом термохимии является закон Гесса, являющийся частным случаем первого начала термодинамики:
Тепловой эффект химической реакции, проводимой в изобарно-изотермических или изохорно-изотермических условиях, зависит только от вида и состояния исходных веществ и продуктов реакции и не зависит от пути её протекания.
Следствия из закона Гесса:
1. Тепловой эффект прямой реакции равен по величине и противоположен по знаку тепловому эффекту обратной реакции (закон Лавуазье – Лапласа).
2. Для двух реакций, имеющих одинаковые исходные, но разные конечные состояния, разность тепловых эффектов представляет собой тепловой эффект перехода из одного конечного состояния в другое.
С + О2 ––> СО + 1/2 О2 ΔН1
С + О2 ––> СО2 ΔН2
СО + 1/2 О2 ––> СО2 ΔН3
 (I.18)
(I.18)
3. Для двух реакций, имеющих одинаковые конечные, но разные исходные состояния, разность тепловых эффектов представляет собой тепловой эффект перехода из одного исходного состояния в другое.
С(алмаз) + О2 ––> СО2 ΔН1
С(графит) + О2 ––> СО2 ΔН2
С(алмаз) ––> С(графит) ΔН3
 (I.19)
(I.19)
4. Тепловой эффект химической реакции равен разности сумм теплот образования продуктов реакции и исходных веществ, умноженных на стехиометрические коэффициенты.
 (I.20)
(I.20)
5. Тепловой эффект химической реакции равен разности сумм теплот сгорания исходных веществ и продуктов реакции, умноженных на стехиометрические коэффициенты.
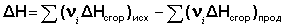 (I.21)
(I.21)
величины тепловых эффектов при данных условиях называют стандартными тепловыми эффектами и обозначают ΔН°298 и ΔU°298 соответственно
Влияние температуры на величины тепловых эффектов описывает закон Кирхгофа:
Температурный коэффициент теплового эффекта химической реакции равен изменению теплоемкости системы в ходе реакции.
 (I.30)
(I.30)
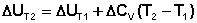 (I.31)
(I.31)
Поскольку обычно известны табличные значения стандартных тепловых эффектов ΔН°298 и ΔU°298, преобразуем выражения (I.30, I.31):
 (I.32)
(I.32)
 (I.33)
(I.33)
При расчете изменения теплового эффекта реакции в большом интервале температур необходимо учитывать зависимость теплоёмкости от температуры, которая выражается степенным рядом C°p = aT + bT2 + cT3; коэффициенты a, b, c приведены в справочниках.
Энтропия
Причина, почему некоторые изменения имеют естественную тенденцию к возникновению, не в том, что система переходит в более низкое энергетическое состояние, а в том, что изменения в системе происходят хаотично. Это можно наблюдать, рассматривая конкретный пример: диффузия одного газа в другой происходит без какого-либо воздействия из вне – то есть происходит самопроизвольно – и тем не менее нет никаких различий ни в потенциальной, ни в кинетической энергии системы в равновесном и в исходном состоянии, в котором два газа изолированы друг от друга. Движущей силой таких процессов является стремление системы к хаосу – система смешанного типа является более разупорядоченной, чем исходная.
Соответствующей мерой хаоса или разупорядоченности системы является энтропия(S). Если система становится более хаотичной, то энтропия возрастает в соответствии со степенью увеличения ее разупорядоченности. Второй закон термодинамики: энтропия изолированной системы возрастает при самопроизвольном ее изменении.
энтропии,∆Sопределяется теплотой поглощенной при обратимом процессе, qrev, деленной на температуру (в Кельвинах), при которой происходит изменение энтропии.
Для измерений имеющих предел
 (3.5)
(3.5)
и для бесконечно малых измерений
 (3.6)
(3.6)
Под «обратимым процессом» мы понимаем процесс, в котором изменения происходят очень медленно, так что система всегда находится в равновесии с окружающей средой. В данном случае мы подразумеваем, что температура окружающей незначительно выше температуры системы, поэтому теплообмен происходит с очень низкой скоростью и становится равномерным и однородным.
Мы можем на конкретных примерах наблюдать связь между энтропией и разупорядоченностью. Например, энтропия идеального газа изменяется согласно соотношению объемов
 (3.7)
(3.7)
где подстрочные индексы f и i обозначают конечное и начальное состояния системы. Обратите внимание, что если Vf>Vi (то есть, если газ расширяется в большем объеме), то логарифмический член будет принимать положительное значение, и мы можем предсказать увеличение энтропии. Это ожидаемо, так как расширение газа — это самопроизвольный процесс, и он будет сопровождаться увеличением разупорядоченности, потому что движение молекул происходит в большем объеме.
Увеличение температуры системы также приводит к увеличению энтропии, так как при более высокой температуре движение молекул становится более интенсивным, следовательно, система становится более хаотичной. Уравнение, показывающее связь между изменением энтропии и изменением температуры
 (3.8)
(3.8)
Где cv это молярная теплоемкость при постоянном объеме. Данное уравнение показывает, что ∆S будет иметь положительное значение в том случае, если Tf>Ti.
Энтропия вещества будет также изменяться при его фазовом переходе, так как это тоже приводит к изменению упорядоченности системы. Например, твердый металл кристаллического строения, он способен переходить из упорядоченной кристаллической решетки в более хаотичное состояние – жидкое, (рис.3.1) и энтропия соответственно будет возрастать. Изменение энтропии, сопровождающей плавление твердого вещества, выражается формулой
 (3.9)
(3.9)
Где ∆Hfus -это энтальпия плавление, а T- это температура плавления. Также мы можем определить изменение энтропии при испарении жидкости
 (3.10)
(3.10)
Где ∆Hvap - это энтальпия испарения, а T - это температура в точке кипения. Изменение энтропии сопровождает и другие фазовые переходы, такие как изменение полиморфной формы кристаллов, ее можно вычислить аналогичным образом.
Абсолютной ноль достигается при прекращении теплового движения атомов кристаллической решетки, и система в данном случае не будет разупорядоченной, следовательно, энтропия будет равна нулю. Этот вывод является основой третьего закона термодинамики, который гласит, что энтропия идеального кристалла равна нулю при T=0.
Одной из формулировок третьего начала термодинамики является также постулат Планка:
Энтропия идеального кристалла при абсолютном нуле температуры равна нулю.
Свободная энергия
· Во время самопроизвольного процесса при постоянной температуре и давлении свободная энергия понижается до тех пор, пока система не достигнет положения равновесия (изменение свободной энергии станет равным нулю). Поэтому свободная энергия является мерой полезной работы, которую может совершить система; если система достигла равновесия, это значит, что она использовала всю свою свободную энергию, и, следовательно, больше не имеет возможности совершать дальнейшую работу; таким образом самопроизвольные процессы являются необратимыми.
· Существует простая связь между свободной энергией и константой равновесия реакции, из которой было выведено уравнение для изменения константы равновесия с температурой.
Свободная энергия выводится из энтропии и, во многих случаях, является более удобной в применении функцией. Свободная энергия, которая упоминалась, когда мы рассматривали процессы, происходящие при постоянном давлении, называется свободной энергией Гиббса.
 (3.11)
(3.11)
Изменение свободной энергии при постоянной температуре среды зависит от изменения энтальпии и энтропии.
 (3.12)
(3.12)
.Таким образом, при постоянной температуре и давлении,
 (3.13)
(3.13)
Где мы видим, что изменение свободной энергии - это другой путь выражения изменения общей энтропии процессов, происходящих при постоянной температуре и давлении.
Благодаря этой взаимосвязи мы можем рассмотреть изменение свободной энергии, которое происходит во время самопроизвольного процесса. Из уравнения (3.13) мы можем увидеть, что ΔG будет уменьшаться в ходе самопроизвольного процесса, происходящего при постоянной температуре и давлении. Уменьшение будет происходить до тех пор, пока система не достигнет равновесного состояния, где ΔG станет равной нулю. Этот процесс можно рассматривать, как постепенное использование способности системы выполнять работу в условиях, приближенных к равновесию. Поэтому свободную энергию можно рассмотреть и с другой стороны, можно представить ее в виде максимального объема работы, wmax (помимо работы, затраченной на расширение), которая может быть совершена системой, подверженной изменению при постоянной температуре и давлении, то есть
 (3.14)
(3.14)
при постоянной температуре и давлении
Работа может быть затрачена системой на совершение электрической работы, как в случае имеющей место химической реакции в электрохимической ячейки, также энергия может накапливаться в биологических молекулах, таких как аденозинтрифосфат (АТФ).
Если система достигнет равновесия, то она больше не сможет изменять направление протекания процесса. Следовательно, все самопроизвольные процессы необратимы. Все самопроизвольные процессы, происходящие при постоянной температуре и давлении, сопровождаются отрицательным изменением свободной энергии, которая является полезным критерием самопроизвольности любого процесса
Применяя эти понятия к химическому равновесию, мы можем управлять следующим взаимоотношением между изменением свободной энергии и равновесной константой обратимой реакции, K:
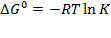
где стандартная свободная энергия G0 – это энергия 1 моля газа при давлении 1 бар
Рассмотрим следующую обратимую реакцию, проходящую в газообразной фазе.
aA + bB = cC + dD
В соответствии с законом действующих масс, константа равновесия К равна:

где p’- парциальное давление компонента в реакции в равновесном состоянии.
Взаимодействие между свободной энергией и парциальным давлением идеального газа задаётся формулой:
G=g-g’=RTlnp
где G’ – свободная энергия в 1 моль газа при давлении в 1 бар.
Применение уравнения (3.16) к каждому компоненту реакции дает:

дельта G – стандартное изменение свободной энергии реакции задаётся формулой:

Как отмечалось ранее, изменение свободной энергии для равновесных систем равно нулю, поэтому уравнение 3.17 приобретает вид:

Уравение 3.20 даёт изменение в свободной энергии, когда a моль вещества А при парциальном давлениии ра и b моль вещества В при парциальном давлении рB реагируют между собой и в качестве продукта получается с моль вещества С при парциальном давлении рс и d моль вещества D при парциальном давлении рD. Чтобы такие реакции протекала самопроизвольно, изменение свободной энергии должно быть отрицательным, и, следовательно, уравнение 3.20 даёт возможность предсказать лёгкий путь реакции для выбранных парциальных давлений (или концентраций) веществ.
Похожее выражение может быть получено для реакций в растворе, используя активность компонентов, а не парциальное давление. Значения G легко могут быть рассчитаны по табличным данным и, поэтому необходимо уравнение (3.19), поскольку оно позволяет рассчитать константу равновесия без проведения опыта.
Рациональным выражением для зависимости температуры от константы равновесия является уравнение Вант-Гоффа, которое может быть получено, как показано в таблице 3.3. Более общая форма данного уравнения:

График от logK к 1/Т должен быть линейным с касательной«минус дельта Н», числовое значение дельта Н которой может быть рассчитано математически.
Уравнения 3.19 и 3.24 являются фундаментальными, нашедшие различное применение в широком спектре фармацевтических наук: например, для определения константы равновесия в химических реакциях или образования мицелл; в обработке информации об устойчивости для некоторых твёрдых дозируемых форм (см. раздел 4.4.3), а также для изучения связи лекарственное вещество – рецептор.
Табоица 3.3 Вывод уравнения Вант– Гоффа

Если предположить, что изменения стандартной энтальпии и стандартной энтропии не зависят от температуры, тогда вычетание уравнения 3.21 из уравнения 3.22 дает: или
Уравнение 3.23, более известное как уравнение Вант-Гоффа, применяется для прогнозирования константы равновесия К2 при температуре Т2 от К1 при другой температуре Т1.
Из Харитоши
1.6 ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ
Изменение энтропии однозначно определяет направление и предел самопроизвольного протекания процесса лишь для наиболее простых систем – изолированных. На практике же большей частью приходится иметь дело с системами, взаимодействующими с окружающей средой. Для характеристики процессов, протекающих в закрытых системах, были введены новые термодинамические функции состояния: изобарно-изотермический потенциал (свободная энергия Гиббса) и изохорно-изотермический потенциал (свободная энергия Гельмгольца).
Поведение всякой термодинамической системы в общем случае определяется одновременным действием двух факторов – энтальпийного, отражающего стремление системы к минимуму тепловой энергии, и энтропийного, отражающего противоположную тенденцию – стремление системы к максимальной неупорядоченности. Если для изолированных систем (ΔН = 0) направление и предел самопроизвольного протекания процесса однозначно определяется величиной изменения энтропии системы ΔS, а для систем, находящихся при температурах, близких к абсолютному нулю (S = 0 либо S = const) критерием направленности самопроизвольного процесса является изменение энтальпии ΔН, то для закрытых систем при температурах, не равных нулю, необходимо одновременно учитывать оба фактора. Направлением и предел самопроизвольного протекания процесса в любых системах определяет более общий принцип минимума свободной энергии:
Самопроизвольно могут протекать только те процессы, которые приводят к понижению свободной энергии системы; система приходит в состояние равновесия, когда свободная энергия достигает минимального значения.
Для закрытых систем, находящихся в изобарно-изотермических либо изохорно-изотермических условиях свободная энергия принимает вид изобарно-изотермического либо изохорно-изотермического потенциалов (т.н. свободная энергия Гиббса и Гельмгольца соответственно). Данные функции называют иногда просто термодинамическими потенциалами, что не вполне строго, поскольку термодинамическими потенциалами являются также внутренняя энергия (изохорно-изэнтропный) и энтальпия (изобарно-изэнтропный потенциал).
Рассмотрим закрытую систему, в которой осуществляется равновесный процесс при постоянных температуре и объеме. Выразим работу данного процесса, которую обозначим Amax (поскольку работа процесса, проводимого равновесно, максимальна), из уравнений (I.53, I.54):
 (I.68)
(I.68)
 (I.69)
(I.69)
Преобразуем выражение (I.69), сгруппировав члены с одинаковыми индексами:
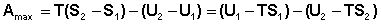 (I.70)
(I.70)
Введя обозначение:
 (I.71)
(I.71)
получаем:
 (I.72)
(I.72)
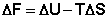 (I.73)
(I.73)
Функция  есть изохорно-изотермический потенциал (свободная энергия Гельмгольца), определяющий направление и предел самопроизвольного протекания процесса в закрытой системе, находящейся в изохорно-изотермических условиях.
есть изохорно-изотермический потенциал (свободная энергия Гельмгольца), определяющий направление и предел самопроизвольного протекания процесса в закрытой системе, находящейся в изохорно-изотермических условиях.
Закрытую систему, находящуюся в изобарно-изотермических условиях, характеризует изобарно-изотермический потенциал G:
 (I.74)
(I.74)
 (I.75)
(I.75)
Поскольку –ΔF = Amax, можно записать:
 (I.76)
(I.76)
Величину А'max называют максимальной полезной работой (максимальная работа за вычетом работы расширения). Основываясь на принципе минимума свободной энергии, можно сформулировать условия самопроизвольного протекания процесса в закрытых системах.
Условия самопроизвольного протекания процессов в закрытых системах:
Изобарно-изотермические (P = const, T = const):
ΔG < 0, dG < 0
ΔF < 0, dF < 0
Процессы, которые сопровождаются увеличением термодинамических потенциалов, протекают лишь при совершении работы извне над системой. В химии наиболее часто используется изобарно-изотермический потенциал, поскольку большинство химических (и биологических) процессов происходят при постоянном давлении. Для химических процессов величину ΔG можно рассчитать, зная ΔH и ΔS процесса, по уравнению (I.75), либо пользуясь таблицами стандартных термодинамических потенциалов образования веществ ΔG°обр; в этом случае ΔG° реакции рассчитывается аналогично ΔН° по уравнению (I.77):
 (I.77)
(I.77)
Величина стандартного изменения изобарно-изотермического потенциала в ходе химической любой реакции ΔG°298 есть мера химического сродства исходных веществ. Основываясь на уравнении (I.75), можно оценить вклад энтальпийного и энтропийного факторов в величину ΔG и сделать некоторые обобщающие заключения о возможности самопроизвольного протекания химических процессов, основываясь на знаке величин ΔН и ΔS.
1. Экзотермические реакции; ΔH < 0.
а) Если ΔS > 0, то ΔG всегда отрицательно; экзотермические реакции, сопровождающиеся увеличением энтропии, всегда протекают самопроизвольно.
б) Если ΔS < 0, реакция будет идти самопроизвольно при ΔН > TΔS (низкие температуры).
2. Эндотермические реакции; ΔH > 0.
а) Если ΔS > 0, процесс будет самопроизвольным при ΔН < TΔS (высокие температуры).
б) Если ΔS < 0, то ΔG всегда положительно; самопроизвольное протекание эндотермических реакций, сопровождающихся уменьшением энтропии, невозможно.
5. Физико-химические свойства лекарственных веществ в растворе. Активность и химический потенциал. Активность и стандартные состояния. Активность ионизированных лекарственных препаратов. Активность растворителя. Химический потенциал.








 (I.4)
(I.4) (I.5)
(I.5) (I.6)
(I.6) (I.8)
(I.8) (I.9)
(I.9) (I.10)
(I.10) (I.11)
(I.11)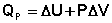 (I.12)
(I.12) (I.13)
(I.13)
 (I.14)
(I.14) (I.15)
(I.15)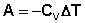 (I.16)
(I.16)

 (I.18)
(I.18) (I.19)
(I.19) (I.20)
(I.20)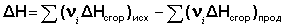 (I.21)
(I.21) (I.30)
(I.30)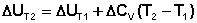 (I.31)
(I.31) (I.32)
(I.32) (I.33)
(I.33) (3.5)
(3.5) (3.6)
(3.6) (3.7)
(3.7) (3.8)
(3.8) (3.9)
(3.9) (3.10)
(3.10) (3.11)
(3.11) (3.12)
(3.12) (3.13)
(3.13) (3.14)
(3.14)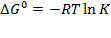



 (I.68)
(I.68) (I.69)
(I.69)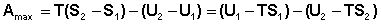 (I.70)
(I.70) (I.71)
(I.71) (I.72)
(I.72)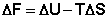 (I.73)
(I.73) (I.74)
(I.74) (I.75)
(I.75) (I.76)
(I.76) (I.77)
(I.77)


