Эксперименты Дж. Гибсона по константности восприятия размера

Дж. Гибсон описывал оригинальные эксперименты, показыва­ющие, что константность размера оцениваемого объекта можно объяснить наличием инвариантной оптической информации — гра­диентом текстуры [34]. Его опыты проводились на большом поле, простиравшемся до горизонта. Оно было хорошо перепахано и выглядело как хорошо текстурированная комочками земли ров­ная поверхность. От испытуемых требовалось оценить высоту стол­биков-вех, которые были расставлены по полю на расстоянии до 800 м от испытуемого. Результаты обнаружили, что обычные не­тренированные испытуемые давали достаточно точные оценки высоты вех, и эти оценки не уменьшались даже тогда, когда они были удалены на 800 м. С увеличением расстояния увеличивался лишь разброс индивидуальных оценок. Таким образом, при изме­нении удаленности воспринимаемого объекта в больших пределах наблюдается константность восприятия его размера.

Рис. 114. Два объекта цилиндрической формы на фоне выраженного гра­диента текстуры. Основания обоих цилиндров покрывают одинаковое чис­ло элементов текстуры, это свидетельствует о равенстве их размеров

Дж. Гибсон сделал принципиальное заключение о природе кон­стантности зрительного восприятия величины объекта: «...наблю­датели неосознанно извлекают определенное инвариантное отно­шение, а размер сетчаточного изображения не играет никакой роли. Независимо от того, насколько далеко находится объект, он пересекает или заслоняет одно и то же число текстурных элемен­тов земли. Это число является инвариантным» [34, 233]. Далее Гиб­сон указывает на еще один мощный оптический инвариант: «На каком бы расстоянии ни находилась веха, отношение, в котором ее делит горизонт, также является инвариантным» (там же). Важ­но, что это не признаки для дальнейшей ментальной переработ­ки, а оптическая информация для прямого восприятия размера объекта (рис. 114).

7.3.5. Измерения инвариантных отношений в восприятии

Ряд экспериментальных исследований обнаружил закономер­ные эффекты взаимодействия между феноменальными парамет­рами зрительного образа. Рассмотрим несколько вариантов изу­ченных перцептивных взаимодействий, которые получили свое выражение в виде так называемых перцептивных уравнений [73]. Это и есть количественное выражение результата взаимодействия различного рода стимульных и феноменальных параметров, ха­рактеризующих разные виды константностей.

Отношение видимой величины и видимой удаленности может быть выражено следующей формулой:

где а — зрительный угол (проксимальная величина объекта); 5 — видимая величина объекта; В — его видимая удаленность; к — коэффициент пропорциональности.

Наглядное следствие из этой формулы дают описанные выше результаты Холвея и Боринга: при а = соп81 видимая величина тес­тового круга пропорциональна его видимой удаленности^ Из нее следует хорошо известный закон зрительного угла: при В = соп$1 видимая величина изменяется пропорционально зрительному углу.

Еще одно классическое подтверждение «работы» этого инва­риантного отношения представляет закон Эммерта: при неизмен­ности площади сетчаточной проекции изменение видимого рас­стояния до экрана, на который проецируется послеобраз, влечет за собой пропорциональное увеличение его видимого размера.

В работах У. Годжела было показано, что при редукции всех зри­тельных признаков¹ наблюдаются интересные феномены, назван­ные им тенденцией к равноудаленности и тенденцией к специфичес­кой удаленности [73]. Тенденция к специфической удаленности заключается в том, что при полной редукции зрительных призна­ков человек склонен воспринимать объекты расположенными на одной и той же удаленности от себя, примерно на 1,5 — 2,5 м. Ана­логичная тенденция к равноудаленности состоит в том, что все видимые объекты кажутся расположенными в одной плоскости.

Третье следствие из данного инвариантного отношения имеет место при 5 = СОП81, тогда, естественно, В = к/а. Это означает, что если известна видимая величина объекта, то видимая удален­ность будет пропорциональна углу зрения. Блестящая иллюстра­ция данного следствия — эксперимент с игральными картами, описанный в главе 5.

И наконец, последнее следствие из описываемого инвариант­ного отношения «видимая величина — видимая удаленность», соб­ственно, и описывает феномен константности видимой величины: видимая величина объекта постоянна, если видимая удаленность изменяется обратно пропорционально величине зрительного угла.

В работах У. Годжела также исследовано и другое инвариантное отношение, связывающее видимую глубину и видимую удаленность²:

¹ Хороший пример восприятия пространства при редукции зрительных при­
знаков дают нам отчеты космонавтов, осуществлявших оценки абсолютной и
относительной удаленности объектов в так называемом безориентированном
космическом пространстве.

² Это соотношение справедливо для удаленностей до двух метров, свыше этого
расстояния в знаменателе формулы параметр В включается без показателя степени.

АО /О² = кг\,

где АО — видимая относительная удаленность; В — видимая аб­солютная удаленность; ц — диспаратность; к — здесь и далее не­который коэффициент пропорциональности.

Кроме того, было установлено инвариантное отношение, свя­зывающее видимую величину, видимую глубину, диспаратность и зрительный угол:

АО/5 = кц/а.

• Его смысл в том, что не только видимая абсолютная удален­ность, но и видимая величина могут определять восприятие глу­бины.

А.Д.Логвиненко описывает и другие инвариантные отноше­ния: «видимая скорость—абсолютная удаленность»:

У/а = ку,

где й — абсолютная удаленность; V — скорость перемещения объек­та по сетчатке; V — видимая скорость.

Необходимо отметить, что проведение исследований инвариан­тных отношений в восприятии чрезвычайно сложное дело, требу­ющее от экспериментатора высокого мастерства, поскольку само изучение эффекта влияния одного феноменального параметра на другое требует создания такой стимул ьной ситуации, при которой были бы исключены влияния других феноменальных признаков.

Демонстрация А. Эймса

Блестящей демонстрации некоторых инвариантных отношений в восприятии пространства мы обязаны А.Эймсу, сконструиро­вавшему специальную комнату; в которой «нарушаются» наши привычные представления о размере и удаленности находящегося там объекта [169].

Иллюзия «комнаты Эймса» заключается в том, что испытуемый смот­рит в эту комнату одним глазом через искусственный зрачок и видит там в ее правом дальнем углу маленького мальчика большого роста, а в ле­вом углу взрослого мужчину... маленького роста (рис. 115). Если туда по­местить двух людей абсолютно одинакового роста, то результат будет тем же: в правом углу — большой человек, в левом — маленький.

Причина этого ошибочного восприятия состоит в конструкции са­мой комнаты. С помощью специально подобранных признаков удаленно­сти (художник особым образом нарисовал окна, стены, пол) создается иллюзия, что комната имеет обычную прямоугольную форму, т.е. види­мая удаленность этих двух человек одинакова, а на самом деле ее пло­щадь представляет трапецию и левый дальний угол комнаты реально расположен от наблюдателя почти вдвое дальше, чем правый (рис. 116).

 

Рис. 115. Что видит испытуемый в комнате Эймса. Мальчик в действи­тельности маленького роста, а мужчина — это обычный и достаточно высокий взрослый человек

Особенно важно, что видимая величина не просто уменьши­лась при увеличении реального расстояния, и, следовательно, при уменьшении размера сетчаточного изображения, а уменьшилась во столько раз, во сколько раз уменьшилось видимое расстояние. Из этой демонстрации следует, что зрительный угол определяет не видимую величину объекта, а отношение видимой величины к видимой удаленности. Что, собственно, и следует из приведенно­го выше перцептивного уравнения. Таким образом, если меняется один из феноменальных параметров (видимая удаленность), то

А что реально... (/)///)2=1,9)

Что видит испытуемый

\ /

\ /

\ /

\ /

\ /

ВА 1т

\ I

\ I

\ I

\ /

\ I

\ /

\/

-V-

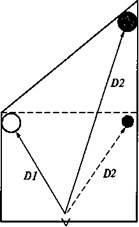
Рис. 116. Соотношение реальных и видимых размеров в комнате Эймса:

слева: видимые размеры самой комнаты, а также видимые размеры и удален­ность двух людей, видимых в комнате Эймса; справа: реальные размеры комнаты и видимые размеры людей. Пунктиром обозначены видимые расстояния и види­мый размер человека. В1 и 02 — физические расстояния от наблюдателя до нахо­дящихся в комнате людей, /)/ и В2 — видимые расстояния [142]

это однозначно приводит к изменению другого феноменального параметра воспринимаемой ситуации (видимый размер).

Интересные эксперименты проводил в комнате Эймса его ученик и последователь Ф. Килпатрик (1954)¹. Его интересовал вопрос, будет ли испытуемый воспринимать пропорции искаженной комнаты адекватно в том случае, если он получит необходимую информацию о ее реальных размерах. Им были проведены три опыта. В первом испытуемый мог сам совершать определенные действия в пространстве этой комнаты, на­пример дотрагиваться указкой до ее стен или бросать мяч в заднюю стенку. Во втором опыте он мог наблюдать, как это делает эксперимен­татор. В третьем — ему рассказывали о том, как реально устроена ком­ната Эймса. Оказалось, что переход к верному восприятию происходил только в первых двух случаях, т.е. когда испытуемый получал наглядные чувственные впечатления о пространственных пропорциях комнаты.

В последние годы появилось и другое объяснение перцептив­ного эффекта, происходящего в комнате Эймса. X. Седвик пред­ложил, что феномен основан не на отношении видимого размера к видимому расстоянию, а на принципе относительного размера. Это объяснение заключается в том, что наше восприятие размера двух людей основано на том, как они собой заполняют расстоя­ние от пола до потолка комнаты Эймса. Поскольку мальчик спра­ва заполняет собой почти все пространство от пола до потолка, а мужчина слева только часть его, то мы и воспринимаем его ниже [209]. Для большей наглядности мы приводим еще один рисунок реальной формы комнаты Эймса с сохранением объемных про­порций ее частей (рис. 117), а не просто план комнаты, как это делается в большинстве учебников (см. рис. 116).

Это объяснение выглядит резонно, и влияние фактора относи­тельного размера на иллюзию восприятия стоит принять во внима­ние естественно не исключая и приведенное выше классическое объяснение, поскольку оно подкрепляется другими исследования­ми инвариантных отношений в зрительном восприятии.

Для тех, кто заинтересовался рассмотренными проблемами, рекомендуем внимательно разобраться с объяснениями так назы­ваемой иллюзии восприятия размера луны [55; 93].