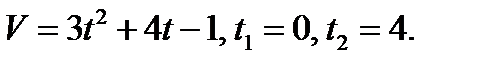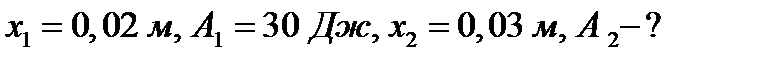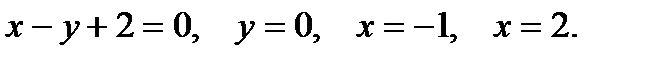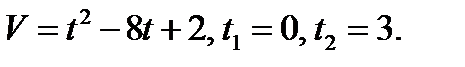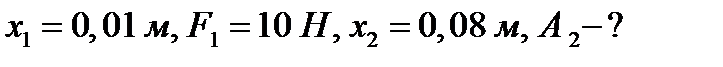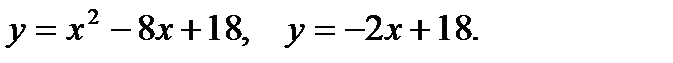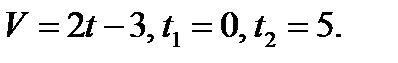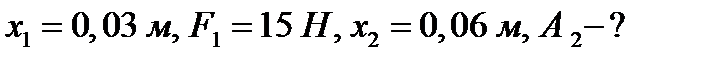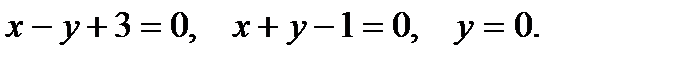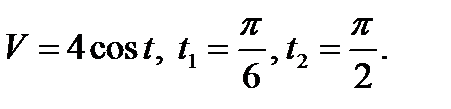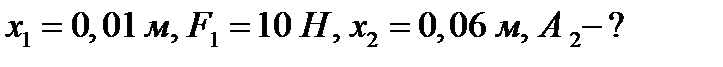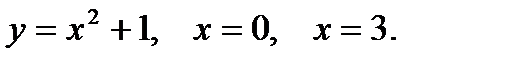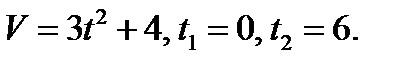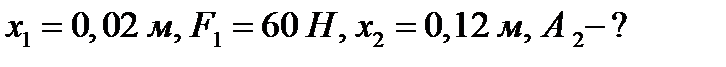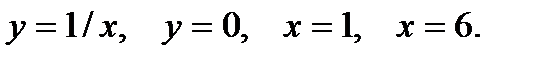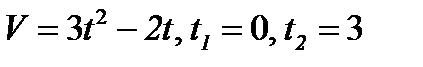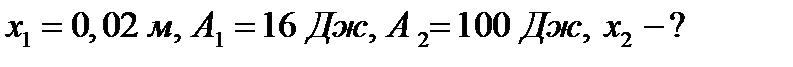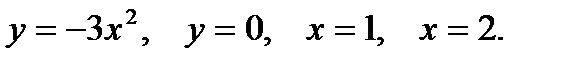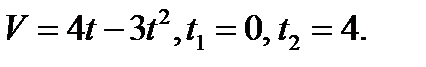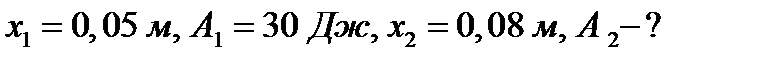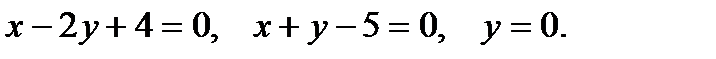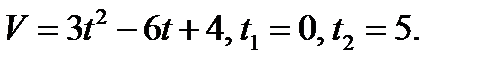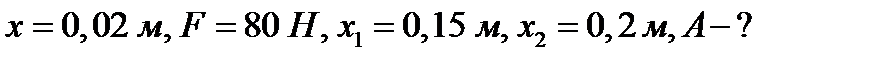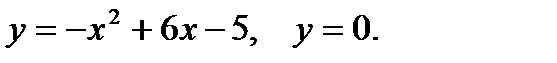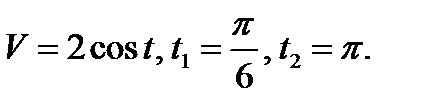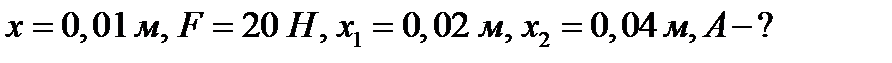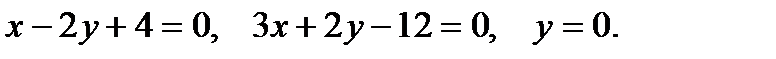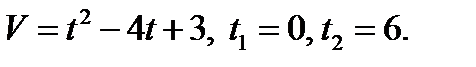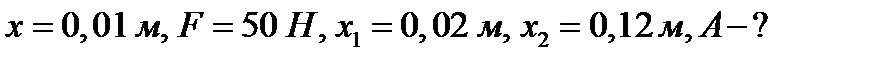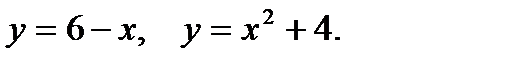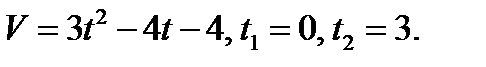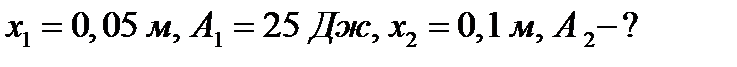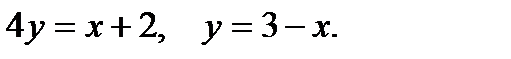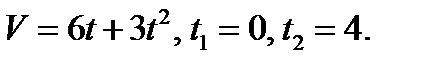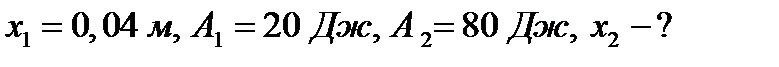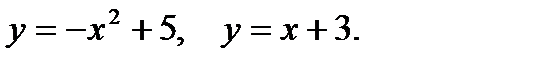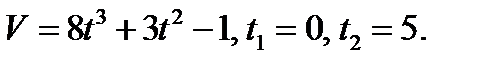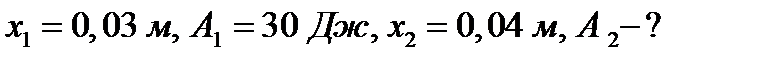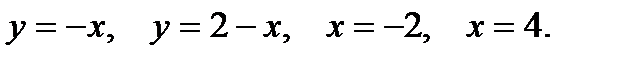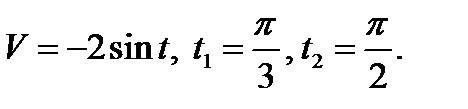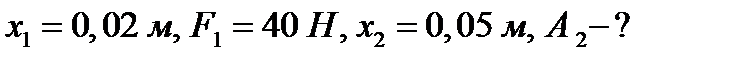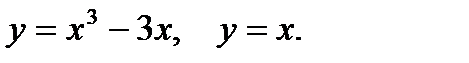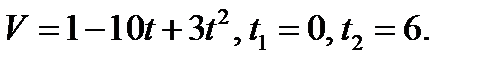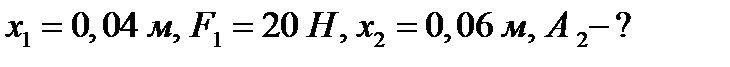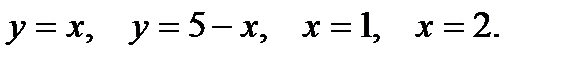К РЕШЕНИЮ ЗАДАЧ
Цель:
- сформировать навыки решения физических задач с помощью определённых интегралов;
- развить умение находить площадь плоской фигуры с помощью определённого интеграла;
Материально – техническое обеспечение: методические указания по выполнению работы, стенды «Таблица интегралов»;
Время выполнения: 2 академических часа;
Ход занятия:
1. Изучить краткие теоретические сведения;
2. Выполнить задания;
3. Сделать вывод по работе;
4. Подготовить защиту работы по контрольным вопросам.
Краткие теоретические сведения:
1. Путь, пройденный точкой. Если точка движется прямолинейно и её скорость 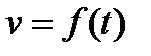 есть известная функция времени t, то путь, пройденный точкой за промежуток времени
есть известная функция времени t, то путь, пройденный точкой за промежуток времени 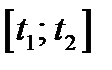 , вычисляется по формуле:
, вычисляется по формуле:
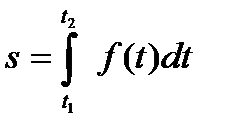 (1)
(1)
Пример 1. Тело движется прямолинейно со скоростью 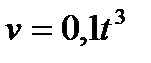 м/с. Вычислить путь, пройденный телом за первые 10с.
м/с. Вычислить путь, пройденный телом за первые 10с.
Решение. Применяя формулу (1), находим искомый путь:
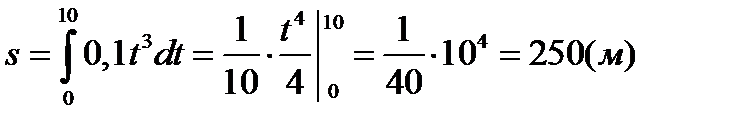
2. Работа силы. Если переменная сила 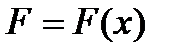 действует в направлении оси Ох, то работа силы на отрезке
действует в направлении оси Ох, то работа силы на отрезке 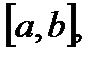 вычисляется по формуле:
вычисляется по формуле:
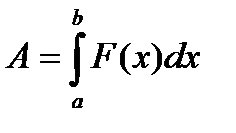 (2)
(2)
Пример 2. Какую работу нужно совершить, чтобы растянуть пружину на 0,06м, если сила 1 Н растягивает ее на 0,01м?
Решение. Согласно закону Гука сила F , растягивающая или сжимающая пружину на x м, равна 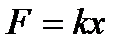 , где
, где 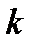 - коэффициент пропорциональности. Из условия следует,
- коэффициент пропорциональности. Из условия следует, 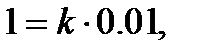 т.е.
т.е. 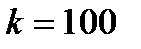 , и, следовательно
, и, следовательно 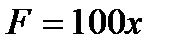 . Искомую работу находим по формуле (2):
. Искомую работу находим по формуле (2):
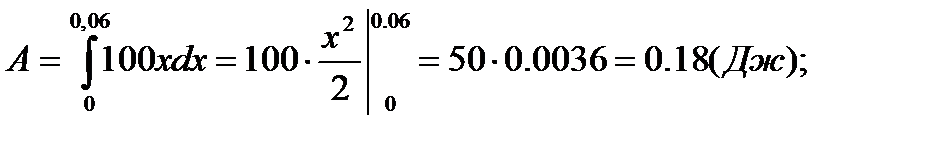
Пример 3. Сила 196,2 Н растягивает пружину на 18 см. Какую работу она производит?
Решение. По закону Гука 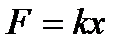 , откуда
, откуда 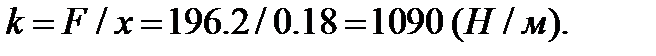
Значит, 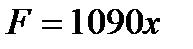 . Находим искомую работу по формуле (2):
. Находим искомую работу по формуле (2):
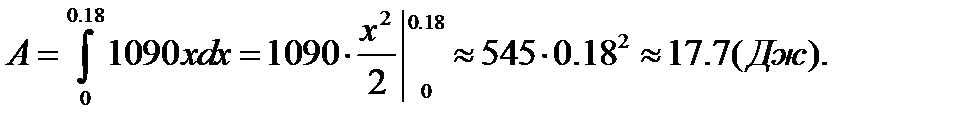
3. Площадь плоской фигуры. Площадь криволинейной трапеции aABb (рис.1), ограниченной графиком непрерывной функции 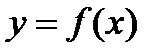 , осью Ох, отрезками прямых
, осью Ох, отрезками прямых 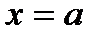 и
и 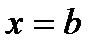 , вычисляется по формуле:
, вычисляется по формуле:
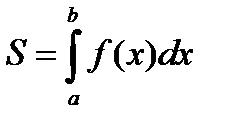 (3)
(3)

Рис.1. Рис.2.
Пример 4. Вычислить площадь фигуры, ограниченной параболой 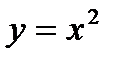 , прямыми
, прямыми 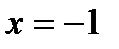 ,
, 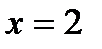 и осью абсцисс (рис.2).
и осью абсцисс (рис.2).
Решение. Применяя формулу (1) , получаем
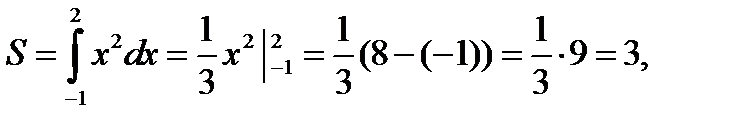 т.е.
т.е. 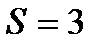 кв.ед.
кв.ед.
Задания для самостоятельного выполнения:
1. Найти путь тела, движущегося с заданной скоростью за данный промежуток времени.
2. Вычислить работу, совершаемую при сжатии или растяжении пружины, пропорционально приложенной силе.
3. Вычислить площадь фигуры, ограниченной данными линиями.
Вариант 1.
1. 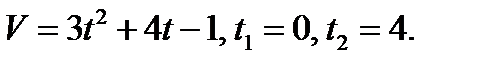
2. 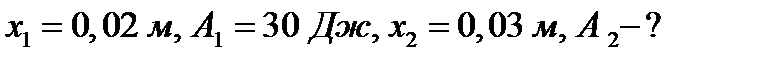
3. 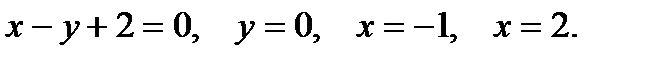
Вариант 2.
1. 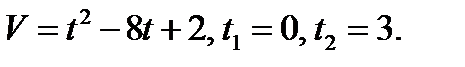
2. 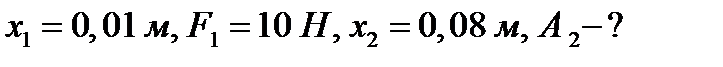
3. 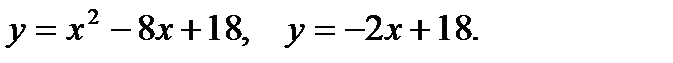
Вариант 3.
1. 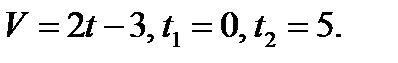
2. 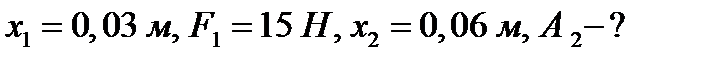
3. 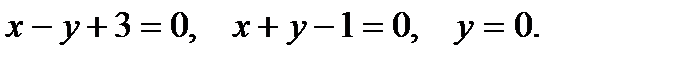
Вариант 4.
1. 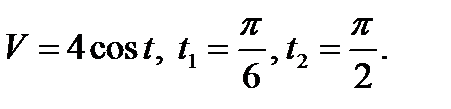
2. 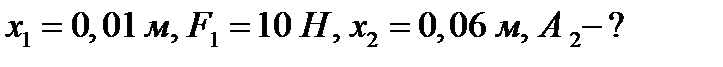
3. 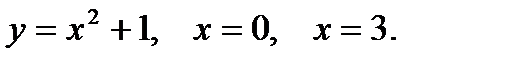
Вариант 5.
1. 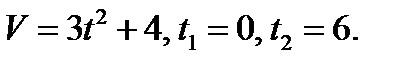
2. 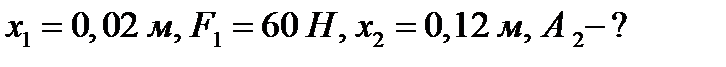
3. 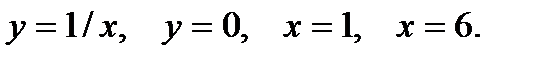
Вариант 6.
1. 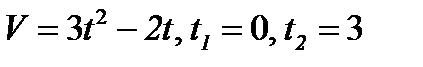
2. 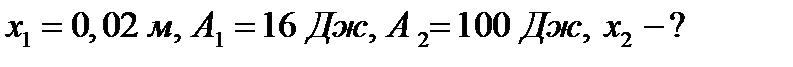
3. 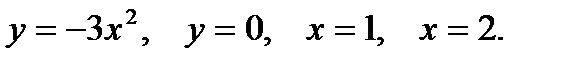
Вариант 7.
1. 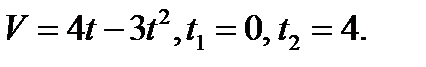
2. 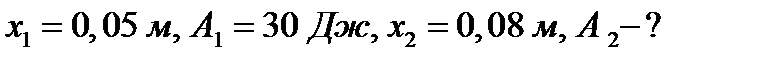
3. 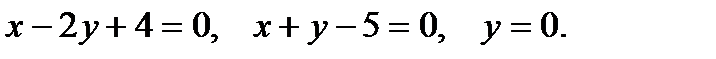
Вариант 8.
1. 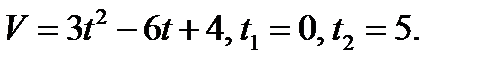
2. 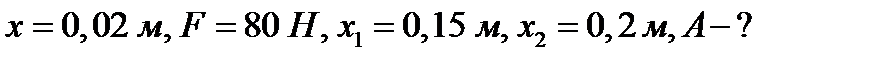
3. 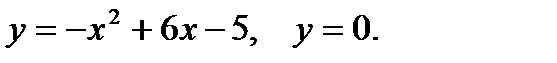
Вариант 9.
1. 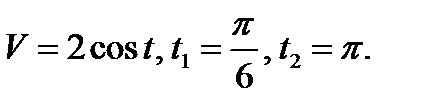
2. 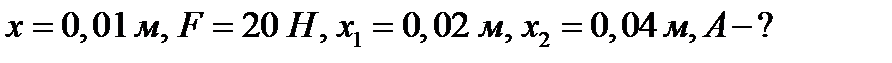
3. 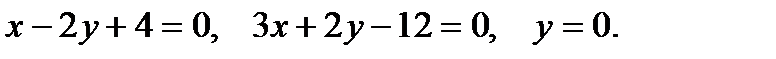
Вариант 10.
1. 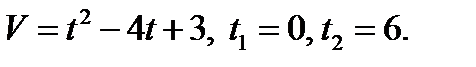
2. 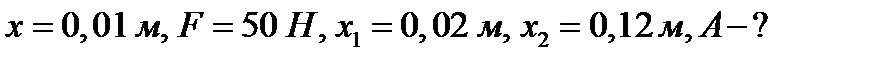
3. 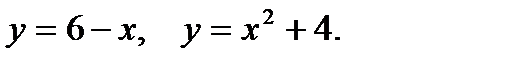
Вариант 11.
1. 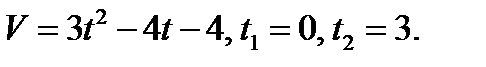
2. 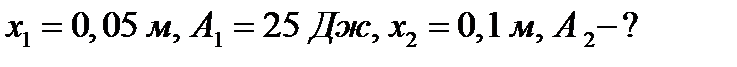
3. 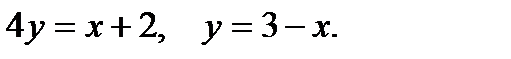
Вариант 12.
1. 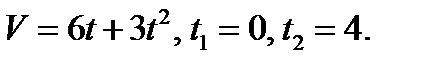
2. 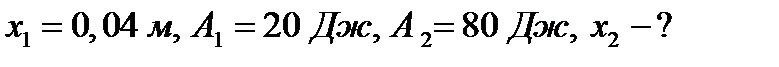
3. 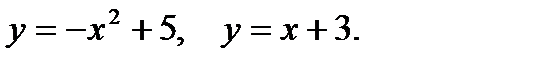
Вариант 13.
1. 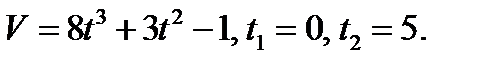
2. 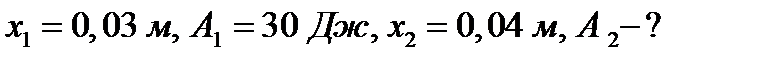
3. 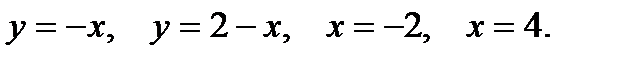
Вариант 14.
1. 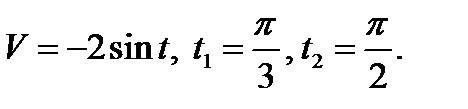
2. 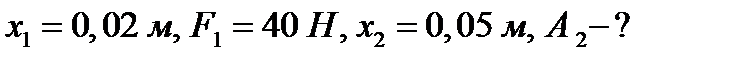
3. 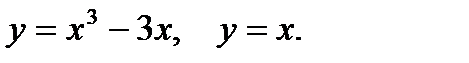
Вариант 15.
1. 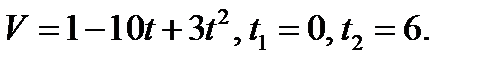
2. 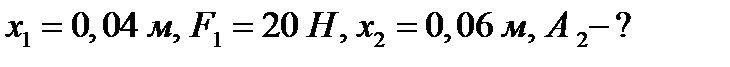
3. 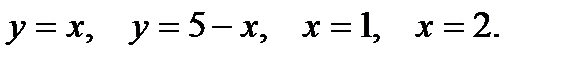
Вопросы для самоконтроля:
1. Как найти путь тела, движущегося с заданной скоростью за данный промежуток времени?
2. Запишите формулу работы, совершаемой при сжатии или растяжении пружины, пропорционально приложенной силе.
3. Сформулируйте правила вычисления площади фигуры, ограниченной заданными линиями?
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 18





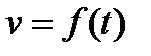 есть известная функция времени t, то путь, пройденный точкой за промежуток времени
есть известная функция времени t, то путь, пройденный точкой за промежуток времени 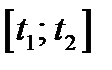 , вычисляется по формуле:
, вычисляется по формуле: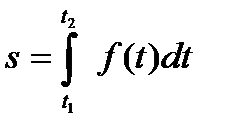 (1)
(1)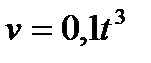 м/с. Вычислить путь, пройденный телом за первые 10с.
м/с. Вычислить путь, пройденный телом за первые 10с.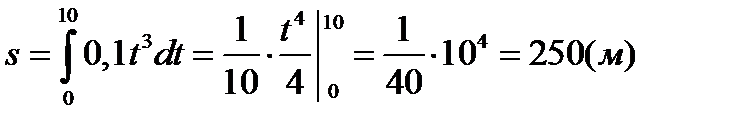
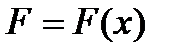 действует в направлении оси Ох, то работа силы на отрезке
действует в направлении оси Ох, то работа силы на отрезке 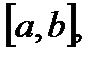 вычисляется по формуле:
вычисляется по формуле: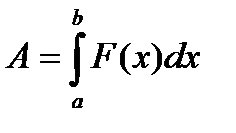 (2)
(2)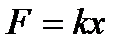 , где
, где 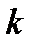 - коэффициент пропорциональности. Из условия следует,
- коэффициент пропорциональности. Из условия следует, 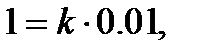 т.е.
т.е. 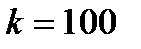 , и, следовательно
, и, следовательно 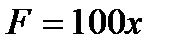 . Искомую работу находим по формуле (2):
. Искомую работу находим по формуле (2):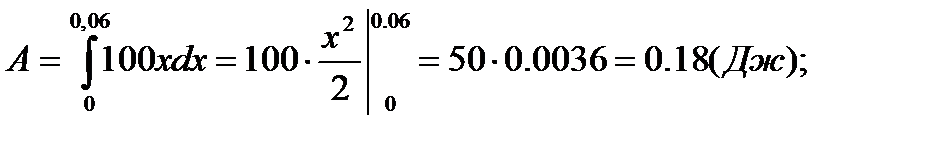
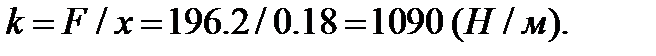
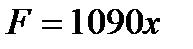 . Находим искомую работу по формуле (2):
. Находим искомую работу по формуле (2):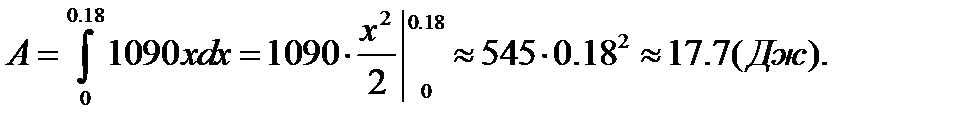
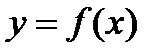 , осью Ох, отрезками прямых
, осью Ох, отрезками прямых 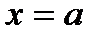 и
и 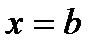 , вычисляется по формуле:
, вычисляется по формуле: 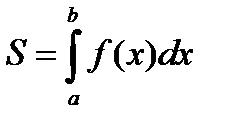 (3)
(3)
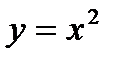 , прямыми
, прямыми 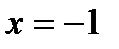 ,
, 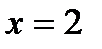 и осью абсцисс (рис.2).
и осью абсцисс (рис.2).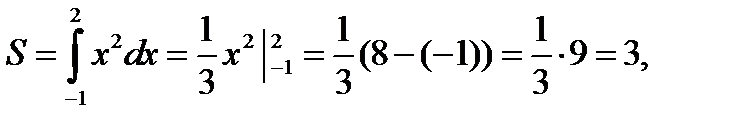 т.е.
т.е. 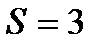 кв.ед.
кв.ед.