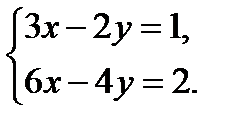Цель:
- сформировать навыки вычисления определителей 2-го порядка;
- развить умение нахождения решения системы двух линейных уравнений с двумя переменными методом Крамера;
- закрепить знания о способах решения уравнений с одной и двумя переменными;
Материально – техническое обеспечение: методические указания по выполнению работы;
Время выполнения: 2 академических часа;
Ход занятия:
1. Изучить краткие теоретические сведения;
2. Выполнить задания;
3. Сделать вывод по работе;
4. Подготовить защиту работы по контрольным вопросам.
Краткие теоретические сведения:
Определителем матрицы 2-го порядка 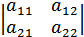 называется число
называется число
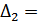
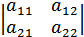 =
= 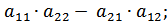
Определитель матрицы 2-го порядка находят по правилу: произведение элементов главной диагонали минус произведение элементов побочной диагонали. Главной диагональю квадратной матрицы называется диагональ, ведущая из левого верхнего угла матрицы в правый нижний угол. Побочной диагональю называется диагональ, ведущая из левого нижнего угла матрицы в правый верхний угол.
Пример 1. Вычислить определитель 2-го порядка 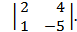
Решение:
Найдём значение определителя по правилу: произведение элементов главной диагонали минус произведение элементов побочной диагонали.
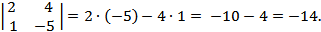
Пример 2. Найти решение системы двух линейных уравнений с двумя неизвестными:
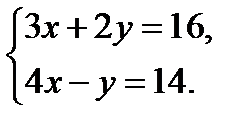
Решение:
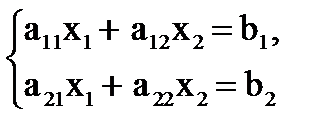 Для системы двух линейных уравнений с двумя неизвестными
Для системы двух линейных уравнений с двумя неизвестными
единственное решение по правилу Крамера находят следующим образом:
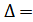
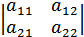 =
= 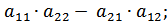
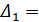
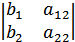 =
= 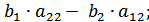
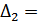
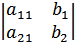 =
= 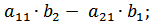
х1 = 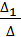 , х2 =
, х2 = 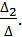
По формулам Крамера получаем:
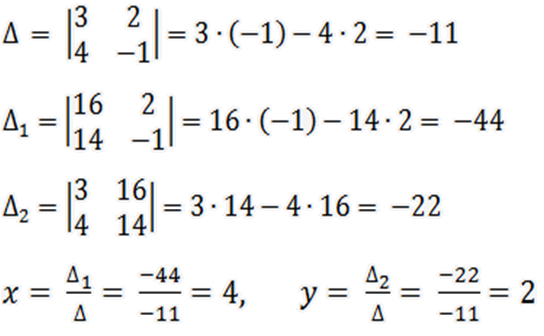
х1 = 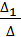 =
= 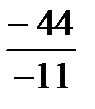 = 4 , х2 =
= 4 , х2 = 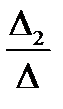 =
= 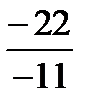 = 2.
= 2.
Ответ: (4;2)
Задания для самостоятельного выполнения:
I. Вычислить определитель второго порядка.
II. Найти корни уравнения.
III. Решить систему двух линейных уравнений с двумя неизвестными методом Крамера.
Вариант 1.
1. 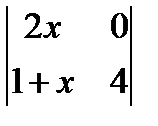 ; 2. х2 +
; 2. х2 + 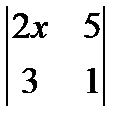 = 0; 3.
= 0; 3. 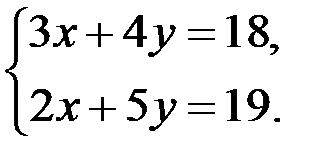
Вариант 2.
1. 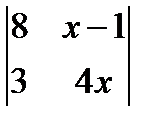 ; 2. х2 +
; 2. х2 + 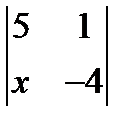 = 0; 3.
= 0; 3. 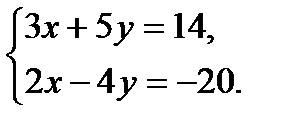
Вариант 3.
1. 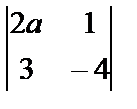 ; 2.
; 2. 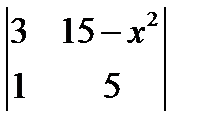 =
= 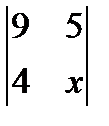 ; 3.
; 3. 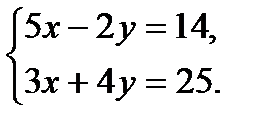
Вариант 4.
1. 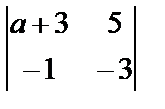 ; 2.
; 2. 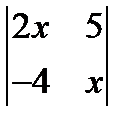 = 36; 3.
= 36; 3. 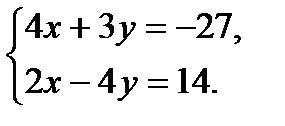
Вариант 5.
1. 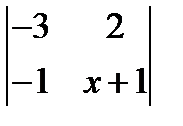 ; 2.
; 2. 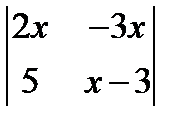 =
= 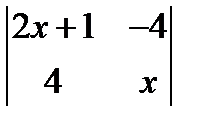 ; 3.
; 3. 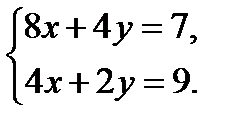
Вариант 6.
1. 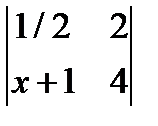 ; 2. х2 -
; 2. х2 -  = 0; 3.
= 0; 3. 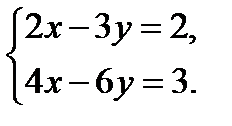
Вариант 7.
1. 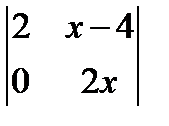 ; 2. х2 +
; 2. х2 + 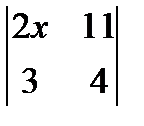 = 0; 3.
= 0; 3. 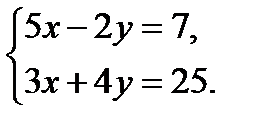
Вариант 8.
1. 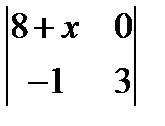 ; 2.
; 2. 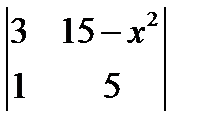 =
= 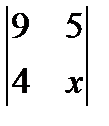 ; 3.
; 3. 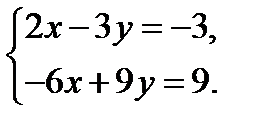
Вариант 9.
1. 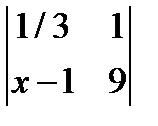 ; 2.
; 2. 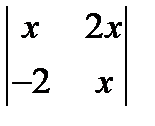 = 32; 3.
= 32; 3. 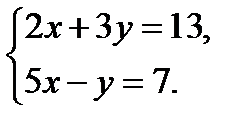
Вариант 10.
1. 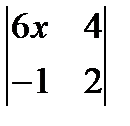 ; 2.
; 2. 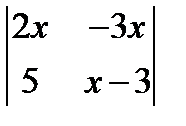 =
= 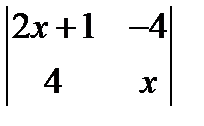 ; 3.
; 3. 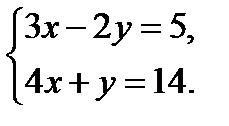
Вариант 11.
1. 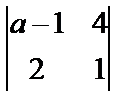 ; 2. х2 -
; 2. х2 - 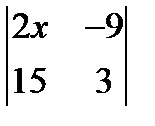 = 0; 3.
= 0; 3. 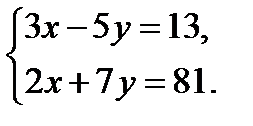
Вариант 12.
1. 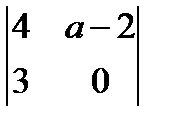 ; 2. х2 -
; 2. х2 - 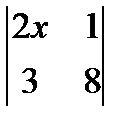 = 0; 3.
= 0; 3. 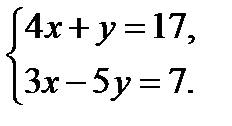
Вариант 13.
1. 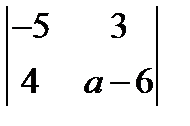 ; 2.
; 2. 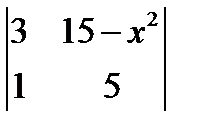 =
= 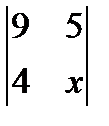 ; 3.
; 3. 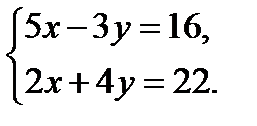
Вариант 14.
1. 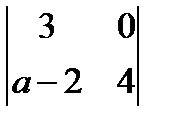 ; 2.
; 2. 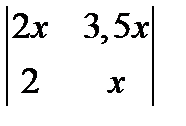 = 15; 3.
= 15; 3. 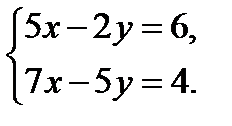
Вариант 15.
1. 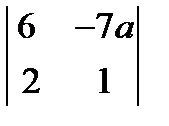 ; 2.
; 2. 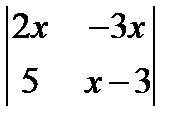 =
= 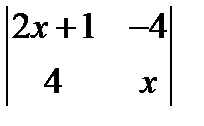 ; 3.
; 3. 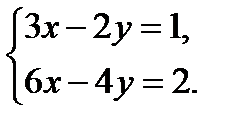
Вопросы для самоконтроля:
1. Что называют определителем второго порядка?
2. Сформулируйте правило вычисления определителя второго порядка.
3. Запишите формулы Крамера для системы двух линейных уравнений с двумя неизвестными.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 5





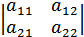 называется число
называется число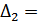
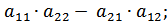
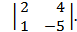
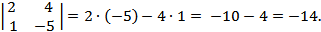
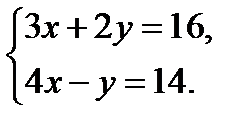
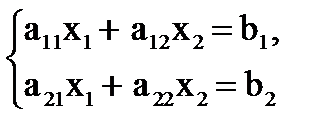 Для системы двух линейных уравнений с двумя неизвестными
Для системы двух линейных уравнений с двумя неизвестными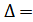
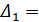
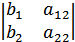 =
= 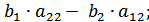
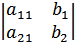 =
= 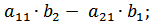
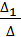 , х2 =
, х2 = 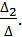
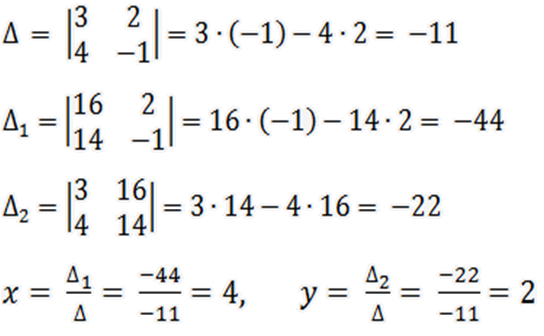
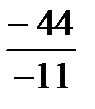 = 4 , х2 =
= 4 , х2 = 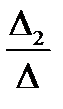 =
= 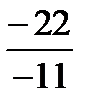 = 2.
= 2.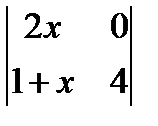 ; 2. х2 +
; 2. х2 + 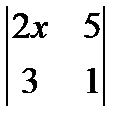 = 0; 3.
= 0; 3. 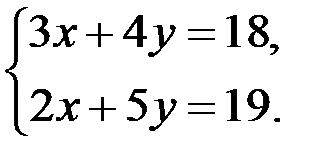
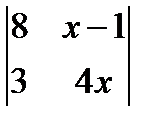 ; 2. х2 +
; 2. х2 + 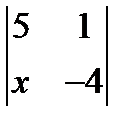 = 0; 3.
= 0; 3. 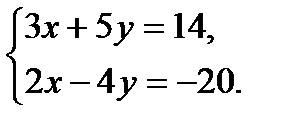
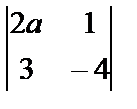 ; 2.
; 2. 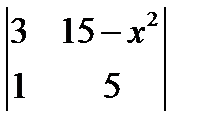 =
=  ; 3.
; 3. 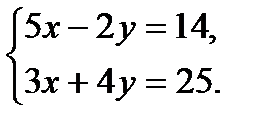
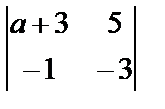 ; 2.
; 2. 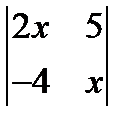 = 36; 3.
= 36; 3. 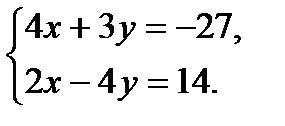
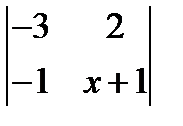 ; 2.
; 2. 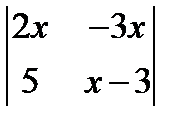 =
= 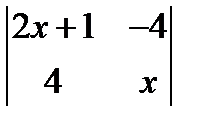 ; 3.
; 3. 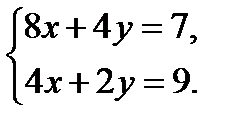
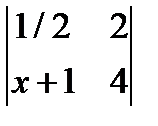 ; 2. х2 -
; 2. х2 -  = 0; 3.
= 0; 3. 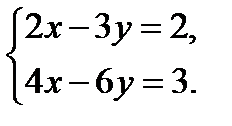
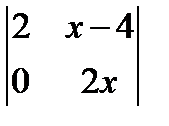 ; 2. х2 +
; 2. х2 + 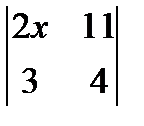 = 0; 3.
= 0; 3. 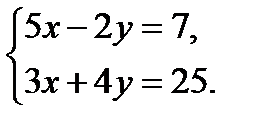
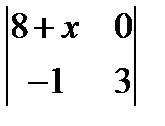 ; 2.
; 2. 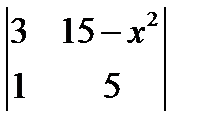 =
=  ; 3.
; 3. 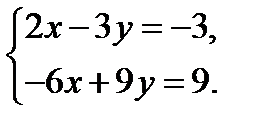
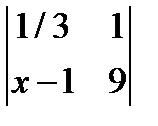 ; 2.
; 2. 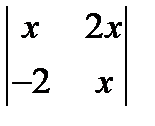 = 32; 3.
= 32; 3. 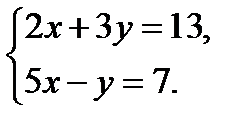
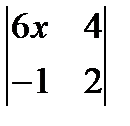 ; 2.
; 2. 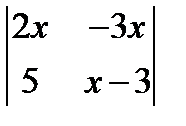 =
= 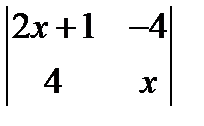 ; 3.
; 3. 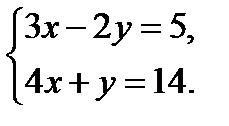
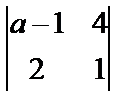 ; 2. х2 -
; 2. х2 - 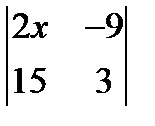 = 0; 3.
= 0; 3. 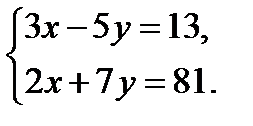
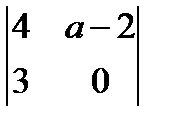 ; 2. х2 -
; 2. х2 - 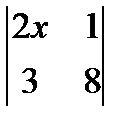 = 0; 3.
= 0; 3. 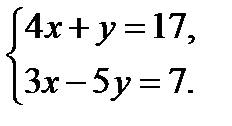
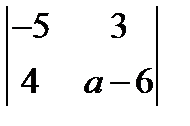 ; 2.
; 2. 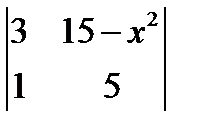 =
=  ; 3.
; 3. 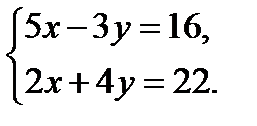
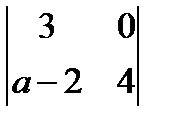 ; 2.
; 2. 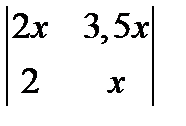 = 15; 3.
= 15; 3. 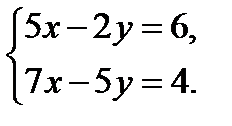
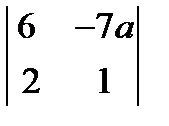 ; 2.
; 2. 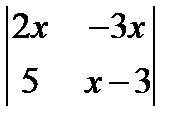 =
= 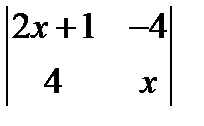 ; 3.
; 3.