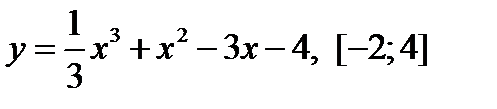Промежутки, в которых график функции обращён выпуклостью вверх или вниз, называются промежутками выпуклости графика функции. Выпуклость графика функции y = f( x) характеризуется знаком её второй производной:
- если в некотором промежутке вторая производная f ´´( x) >0, то график функции выпуклый вниз в этом промежутке;
- если в некотором промежутке вторая производная f ´´( x) <0, то график функции выпуклый вверх в этом промежутке.
Точка графика функции y = f( x), разделяющая промежутки выпуклости противоположных направлений, называется точкой перегиба. Точками перегиба могут служить только критические точки, в которых вторая производная f ´´( x) равна нулю или терпит разрыв. Если при переходе через критическую точку х0 вторая производная f ´´( x) меняет знак, то график функции имеет точку перегиба (х0;у0).
Алгоритм исследования функции на выпуклость и точку перегиба:
1. Найти вторую производную функции у´´.
2. Приравнять y´´ к нулю, решить уравнение, найти критические точки.
3. Исключить критические точки из области определения 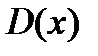 , указать интервалы знакопостоянства y´´.
, указать интервалы знакопостоянства y´´.
4. На каждом интервале определить знак второй производной y´´.
5. По знаку производной y´´ установить направление выпуклости графика функции: при y´´ >0 график выпуклый вниз ∪, при y´´ <0 график выпуклый вверх ∩.
6. Найти точку перегиба, если она существует.
7. Результаты исследования занести в таблицу.
8. Построить схематический график данной функции.
Пример 2. Исследовать функцию 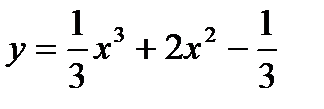 на выпуклость и точку перегиба.
на выпуклость и точку перегиба.
Решение:
1) 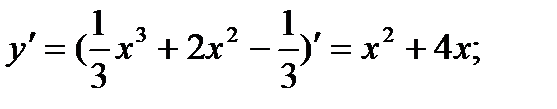
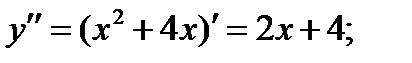
2) 2х + 4 = 0; х = -2 – крит. точка
3) 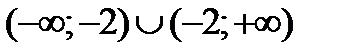
4) 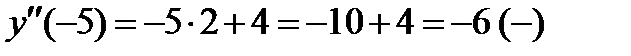 ;
;
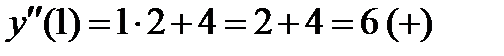
- + f ’’(x)
-2
5) 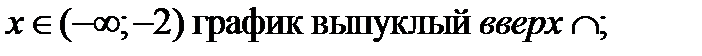
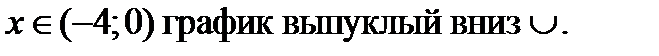
6) Точка перегиба существует при х = -2. Найдём ординату этой точки: у(-2)= 5.
Итак, (-2;5) – точка перегиба.
7) Результаты исследования:
| х
| 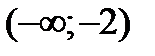
| -2
| 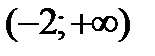
|
| y´´
| -
| 0
| +
|
| у
| ∩
| 5
| ∪
|
8) График функции 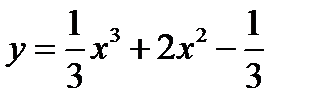 изображён на рис.2
изображён на рис.2
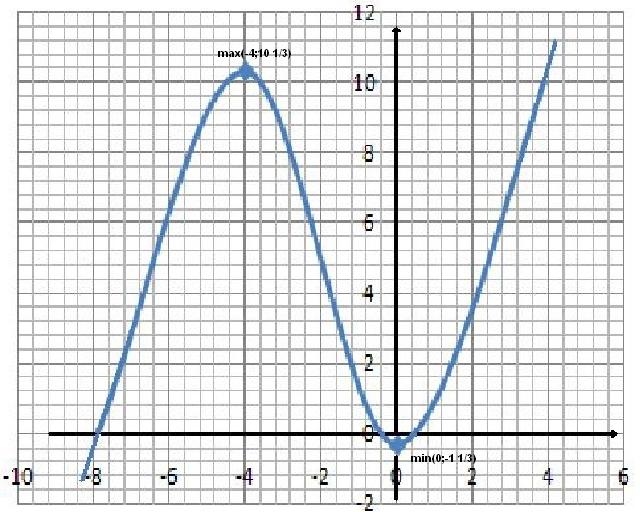
Наибольшее и наименьшее значение функции на промежутке.
Для нахождения наибольшего и наименьшего значений функции y = f( x), непрерывной на некотором промежутке [a;b], необходимо:
1. Найти производную функции у´.
2. Найти критические точки – точки, в которых у´ = 0.
3. Отобрать критические точки, лежащие внутри промежутка [a;b].
4. Вычислить значения функций в выбранных точках и на концах промежутка [a;b].
5. Из полученных значений определить наибольшее и наименьшее значения: max f(x) и min f(x).
Пример 3. Найти наибольшее и наименьшее значения функции 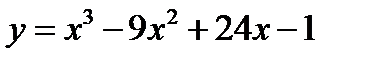 на отрезке [-1;3].
на отрезке [-1;3].
Решение:
1. 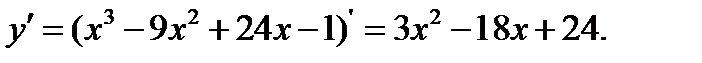
2. 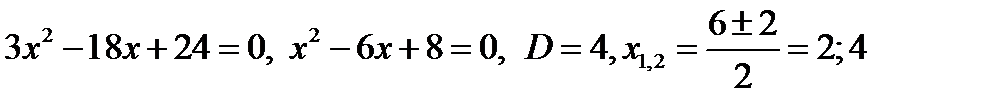 .
.
3. Из найденных критических точек внутри отрезка [-1;3] лежит только х = 2.
4. Найдём значения функции 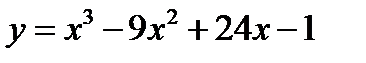 в точке х=2 и на концах отрезка [-1;3]: у(-1) = -35, у(2) = 19, у(3) = 17.
в точке х=2 и на концах отрезка [-1;3]: у(-1) = -35, у(2) = 19, у(3) = 17.
5. Очевидно, что уmax (2) = 19, уmin (-1) = -35.
Задания для самостоятельного выполнения:
1. Исследовать функцию на монотонность и экстремум.
2. Исследовать функцию на выпуклость и точку перегиба.
3. Найти наибольшее и наименьшее значения функции на промежутке.
Вариант 1.
1. 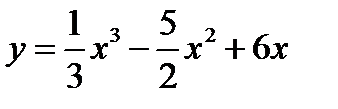 2.
2. 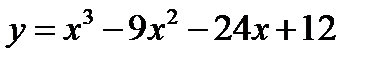 3.
3. 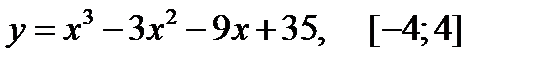 .
.
Вариант 2.
1. 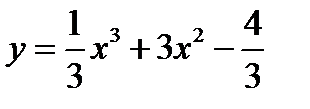 2.
2. 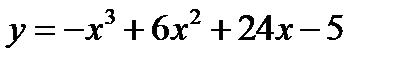 3.
3. 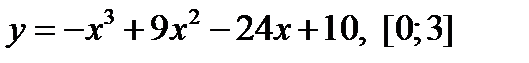 .
.
Вариант 3.
1. 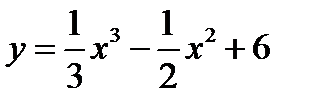 2.
2. 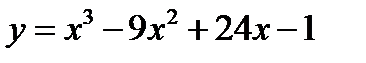 3.
3. 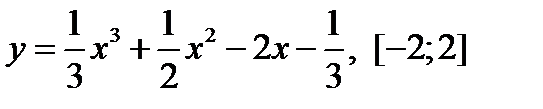 .
.
Вариант 4.
1. 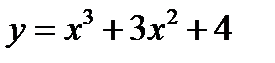 2.
2. 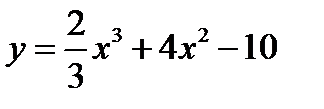 3.
3. 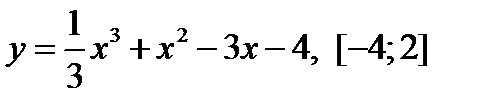 .
.
Вариант 5.
1. 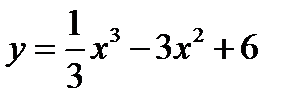 2.
2. 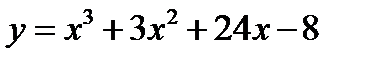 3.
3. 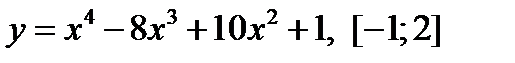 .
.
Вариант 6.
1. 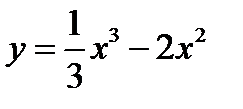 2.
2. 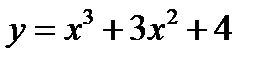 3.
3. 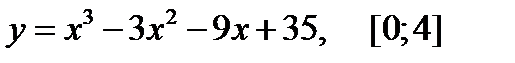
Вариант 7.
1. 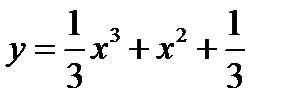 2.
2. 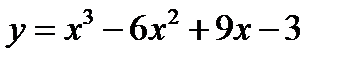 3.
3. 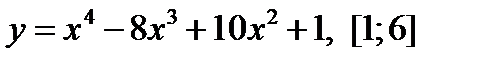
Вариант 8.
1. 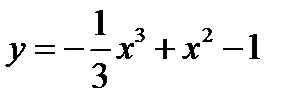 2.
2. 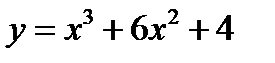 3.
3. 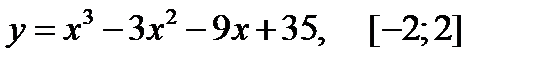
Вариант 9.
1. 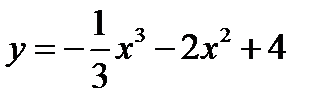 2.
2. 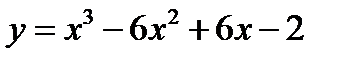 3.
3. 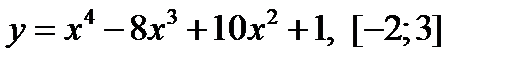
Вариант 10.
1. 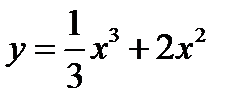 2.
2. 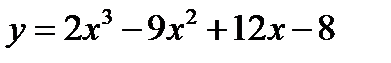 3.
3. 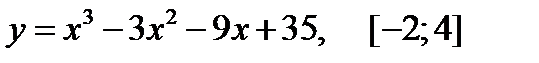
Вариант 11.
1. 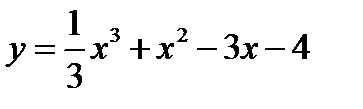 2.
2. 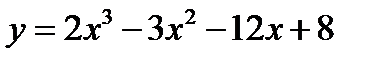 3.
3. 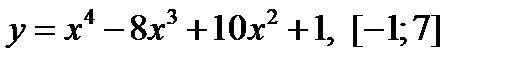
Вариант 12.
1. 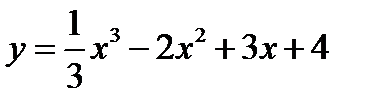 2.
2. 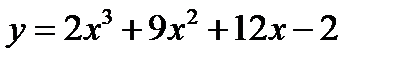 3.
3. 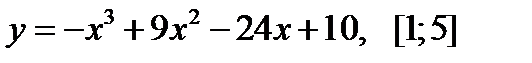
Вариант 13.
1. 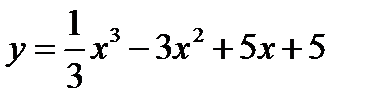 2.
2. 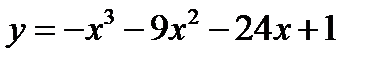 3.
3. 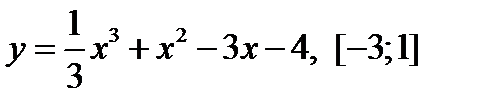
Вариант 14.
1. 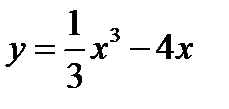 2.
2. 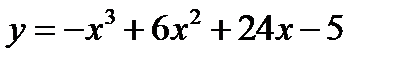 3.
3. 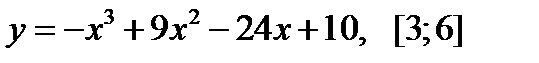
Вариант 15.
1. 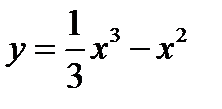 2.
2. 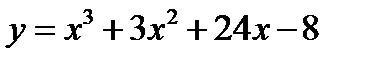 3.
3. 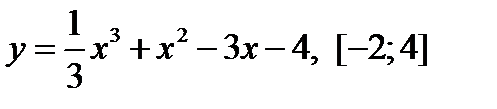
Вопросы для самоконтроля:
1. Как исследовать функцию на монотонность?
2. Что такое экстремумы функции?
3. Как исследовать функцию на выпуклость и точку перегиба?
4. Как найти наибольшее и наименьшее значения функции на промежутке?
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 14





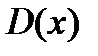 , указать интервалы знакопостоянства y´´.
, указать интервалы знакопостоянства y´´.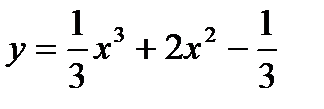 на выпуклость и точку перегиба.
на выпуклость и точку перегиба.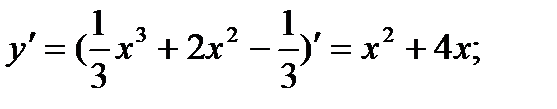
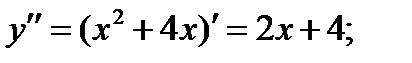
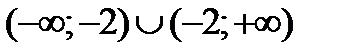
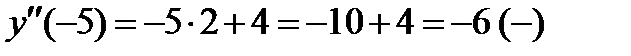 ;
;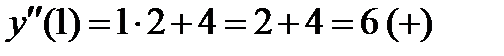
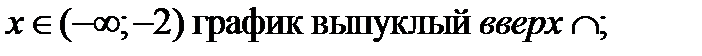
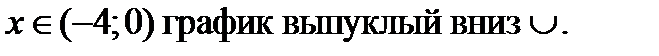
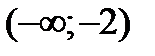
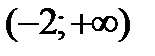
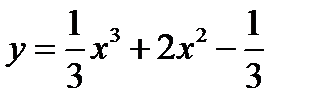 изображён на рис.2
изображён на рис.2
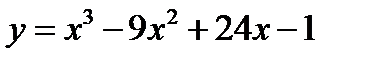 на отрезке [-1;3].
на отрезке [-1;3].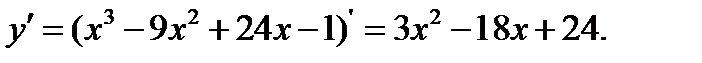
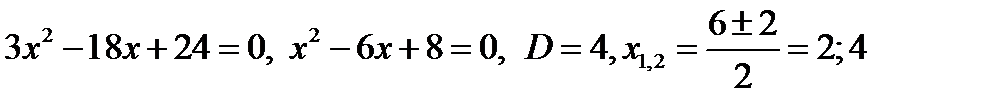 .
.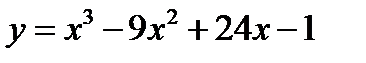 в точке х=2 и на концах отрезка [-1;3]: у(-1) = -35, у(2) = 19, у(3) = 17.
в точке х=2 и на концах отрезка [-1;3]: у(-1) = -35, у(2) = 19, у(3) = 17.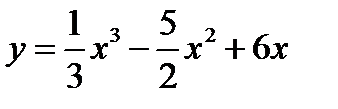 2.
2. 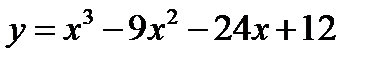 3.
3. 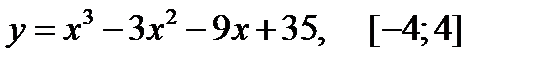 .
. 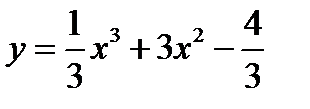 2.
2. 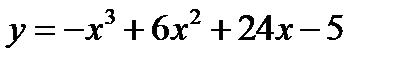 3.
3. 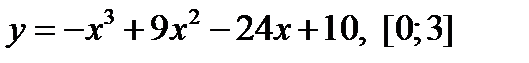 .
. 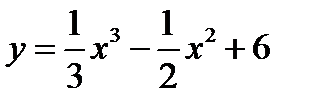 2.
2. 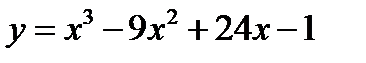 3.
3. 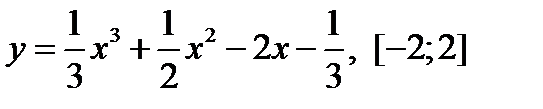 .
. 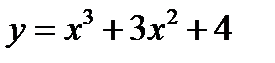 2.
2. 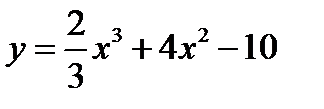 3.
3. 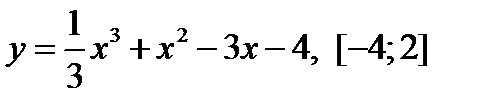 .
. 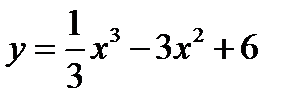 2.
2. 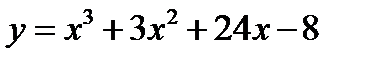 3.
3. 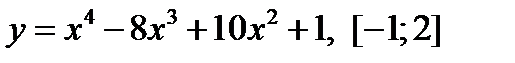 .
. 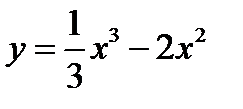 2.
2. 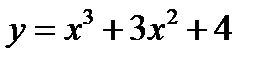 3.
3. 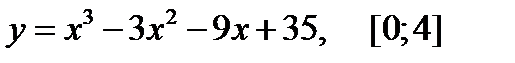
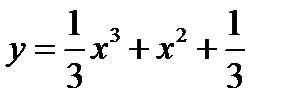 2.
2. 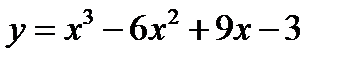 3.
3. 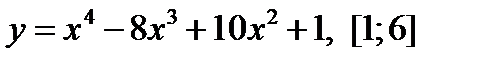
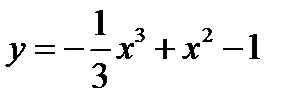 2.
2. 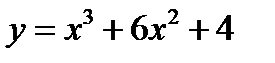 3.
3. 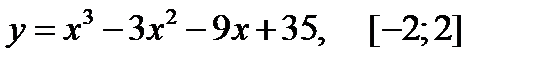
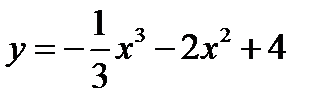 2.
2. 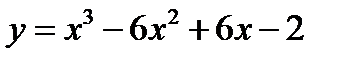 3.
3. 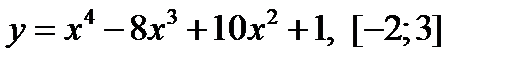
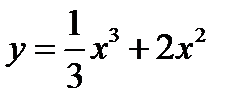 2.
2. 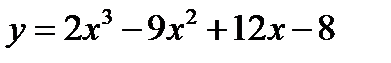 3.
3. 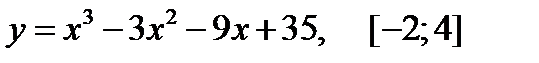
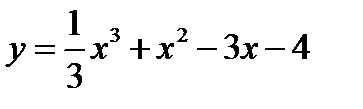 2.
2. 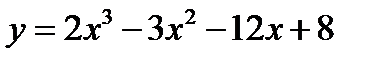 3.
3. 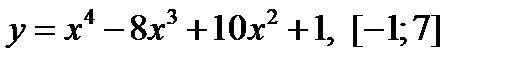
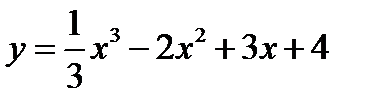 2.
2. 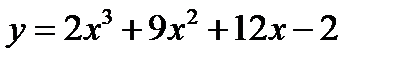 3.
3. 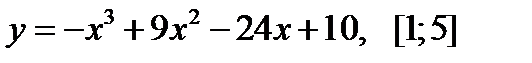
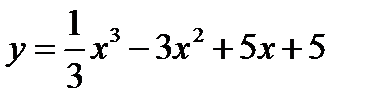 2.
2. 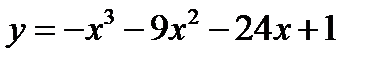 3.
3. 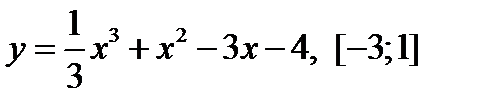
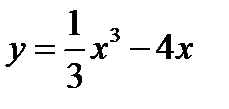 2.
2. 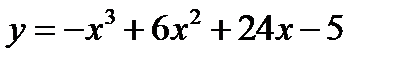 3.
3. 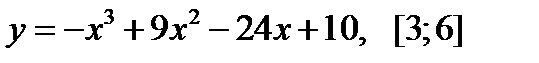
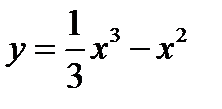 2.
2.  3.
3.