Цель:
- сформировать навыки вычисления определителей 3-го порядка методом разложения по элементам первой строки и по правилу треугольников;
- развить умение преобразования определителя по его свойствам;
- закрепить знания о действиях с числами противоположных знаков;
Материально – техническое обеспечение: методические указания по выполнению работы;
Время выполнения: 2 академических часа;
Ход занятия:
1. Изучить краткие теоретические сведения;
2. Выполнить задания;
3. Сделать вывод по работе;
4. Подготовить защиту работы по контрольным вопросам.
Краткие теоретические сведения:
Определителем матрицы третьего порядка называется число, определяемое равенством:
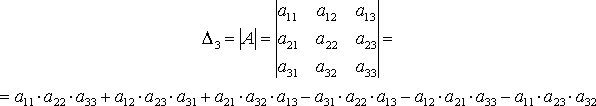 .
.
Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.

Рис.1.1. Рис.1.2.
Знаки, с которыми члены определителя входят в формулу нахождения определителя третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из рисунка (1.1.), а последующие три слагаемые берутся со знаком минус и определяются из рисунка (1.2).
Пример 1. Вычислить определитель третьего порядка по правилу Сарруса:
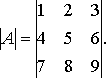
Решение:
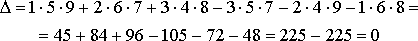
Пример 2. Вычислить определитель третьего порядка методом разложения по элементам первой строки:
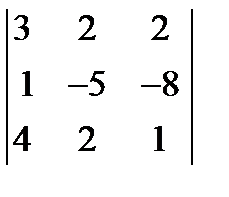 ;
;
Решение:
Используем формулу:

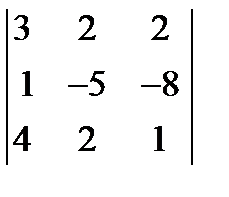 = 3
= 3 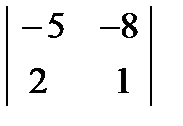 -2
-2 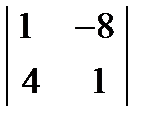 +2
+2 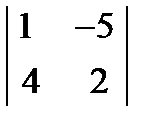 = 3(-5 + 16) – 2( 1+32) + 2( 2 + 20)= = 33 – 66 + 44 = 11.
= 3(-5 + 16) – 2( 1+32) + 2( 2 + 20)= = 33 – 66 + 44 = 11.
Рассмотрим основные свойства определителей:
· Определитель с нулевой строкой (столбцом) равен нулю.
· Если у матрицы умножить любую строку (любой столбец) на какое-либо число, то определитель матрицы умножится на это число.
· Определитель не меняется при транспонировании матрицы.
· Определитель меняет знак при перестановке любых двух строк (столбцов) матрицы.
· Определитель матрицы с двумя одинаковыми строками (столбцами) равен нулю.
· Определитель не меняется, если к какой-нибудь строке прибавить любую другую строку, умноженную на любое число. Аналогичное утверждение справедливо и для столбцов.
Задания для самостоятельного выполнения:
I. Найдите значение определителя по правилу треугольников (правило Сарруса).
II. Разложите определитель по элементам первой строки и вычислите его.
III. Используя свойства определителя, докажите равенство.
Вариант 1.
1. 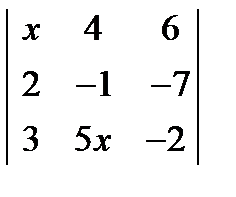 ; 2.
; 2. 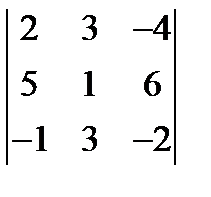 ; 3.
; 3. 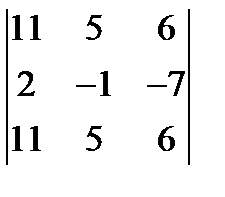 = 0;
= 0;
Вариант 2.
1. 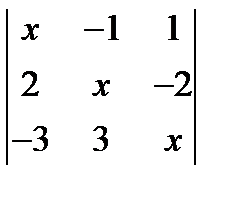 ; 2.
; 2. 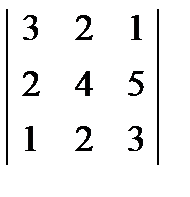 ; 3.
; 3. 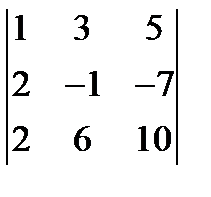 = 0;
= 0;
Вариант 3.
1. 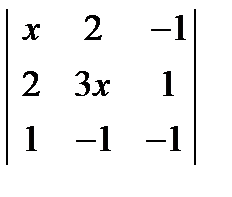 ; 2.
; 2. 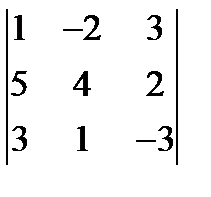 ; 3.
; 3. 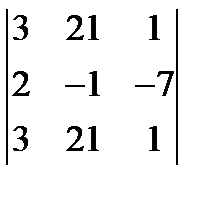 = 0;
= 0;
Вариант 4.
1. 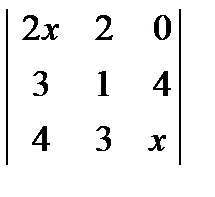 ; 2.
; 2. 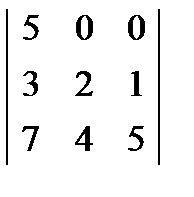 ; 3.
; 3. 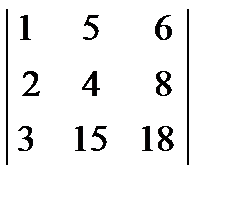 = 0;
= 0;
Вариант 5.
1. 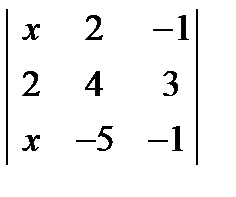 ; 2.
; 2. 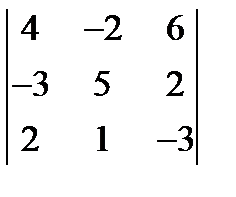 ; 3.
; 3. 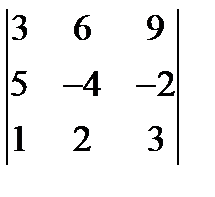 = 0.
= 0.
Вариант 6.
1. 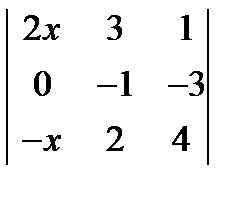 ; 2.
; 2. 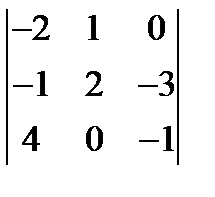 ; 3.
; 3. 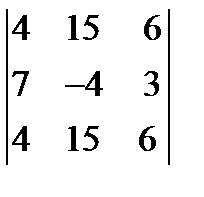 = 0.
= 0.
Вариант 7.
1. 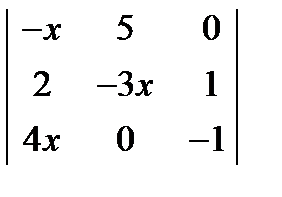 ; 2.
; 2. 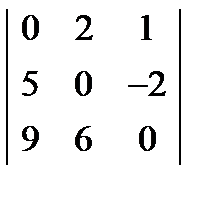 ; 3.
; 3. 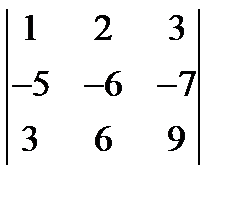 = 0.
= 0.
Вариант 8.
1. 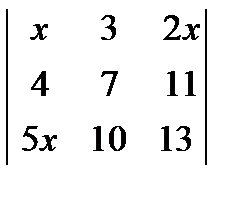 ; 2.
; 2. 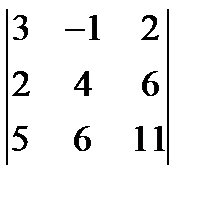 ; 3.
; 3. 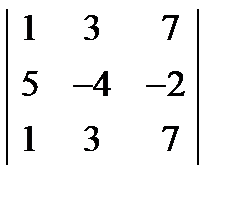 = 0.
= 0.
Вариант 9.
1. 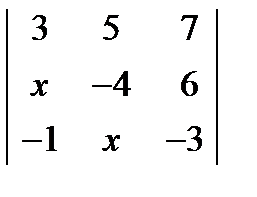 ; 2.
; 2.  ; 3.
; 3. 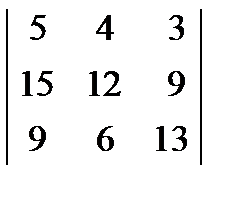 = 0.
= 0.
Вариант 10.
1. 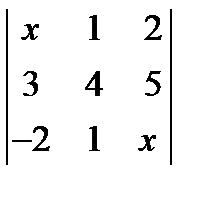 ; 2.
; 2. 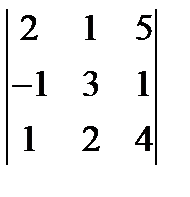 ; 3.
; 3. 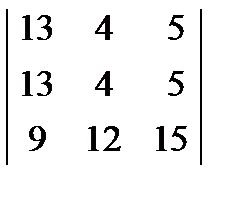 = 0.
= 0.
Вариант 11.
1. 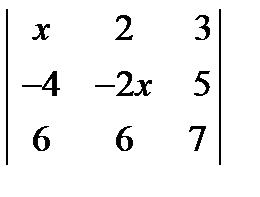 ; 2.
; 2. 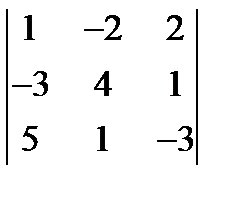 ; 3.
; 3. 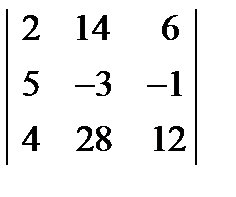 = 0.
= 0.
Вариант 12.
1. 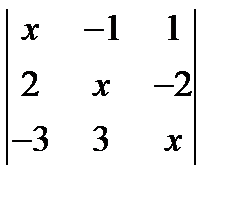 ; 2.
; 2. 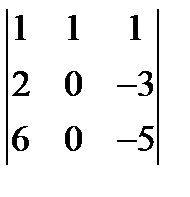 ; 3.
; 3. 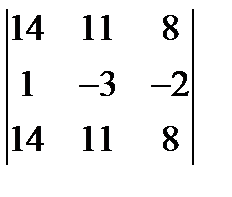 = 0.
= 0.
Вариант 13.
1. 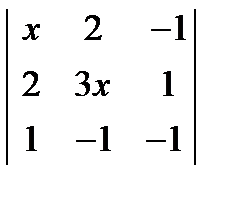 ; 2.
; 2. 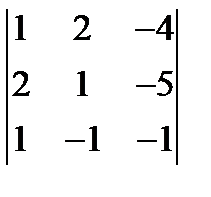 ; 3.
; 3. 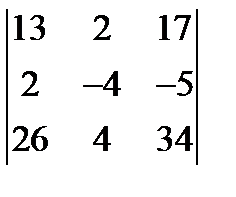 = 0.
= 0.
Вариант 14.
1. 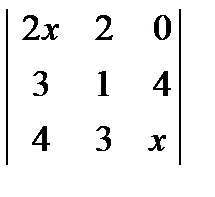 ; 2.
; 2. 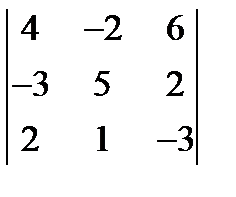 ; 3.
; 3. 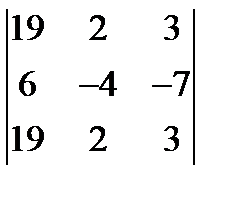 = 0.
= 0.
Вариант 15.
1. 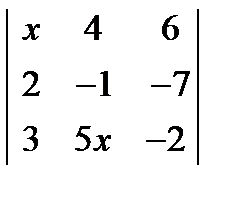 ; 2.
; 2. 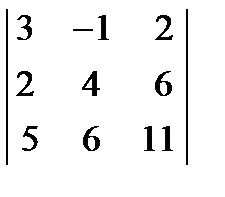 ; 3.
; 3. 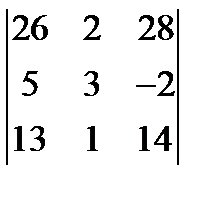 = 0.
= 0.
Вопросы для самоконтроля:
1. Что называют определителем третьего порядка?
2. Сформулируйте правило треугольников для вычисления определителя третьего порядка.
3. Запишите формулу разложения определителя третьего порядка по элементам первой строки.
4. Назовите основные свойства определителя.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 6





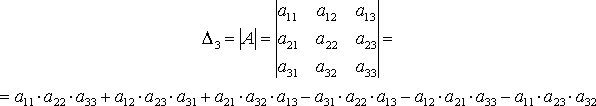 .
.
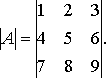
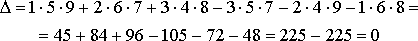
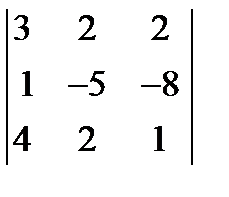 ;
;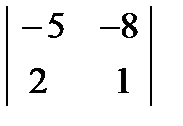 -2
-2 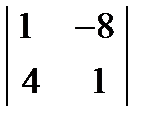 +2
+2 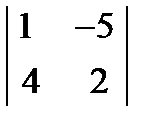 = 3(-5 + 16) – 2( 1+32) + 2( 2 + 20)= = 33 – 66 + 44 = 11.
= 3(-5 + 16) – 2( 1+32) + 2( 2 + 20)= = 33 – 66 + 44 = 11.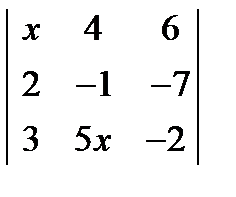 ; 2.
; 2. 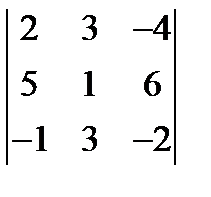 ; 3.
; 3. 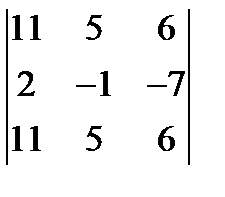 = 0;
= 0; 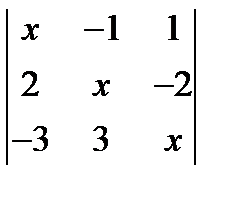 ; 2.
; 2.  ; 3.
; 3. 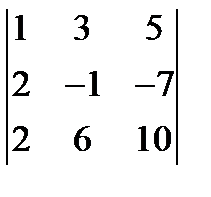 = 0;
= 0; 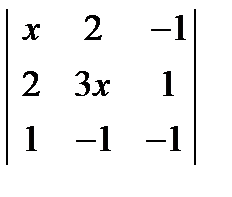 ; 2.
; 2. 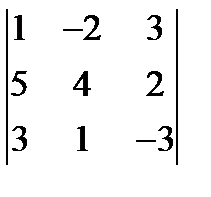 ; 3.
; 3. 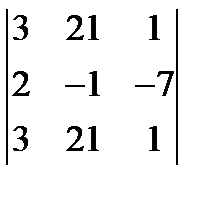 = 0;
= 0; 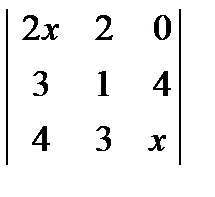 ; 2.
; 2.  ; 3.
; 3. 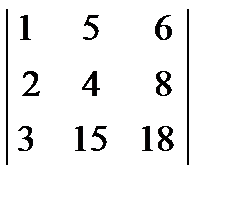 = 0;
= 0; 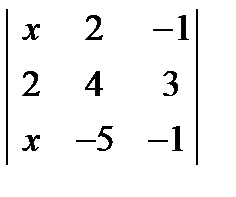 ; 2.
; 2. 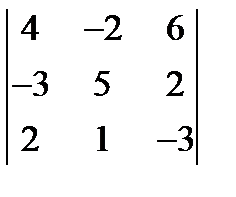 ; 3.
; 3. 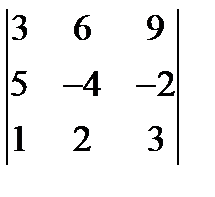 = 0.
= 0.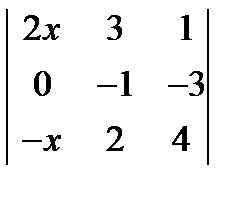 ; 2.
; 2. 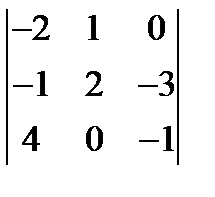 ; 3.
; 3. 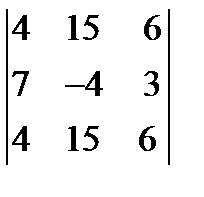 = 0.
= 0.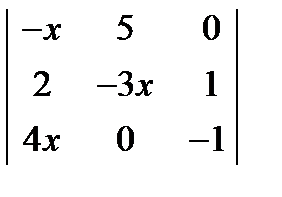 ; 2.
; 2. 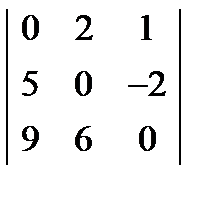 ; 3.
; 3. 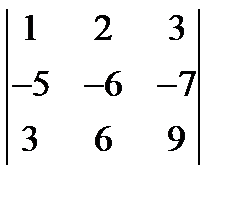 = 0.
= 0.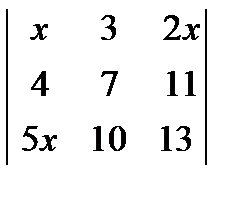 ; 2.
; 2. 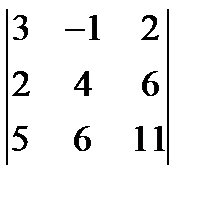 ; 3.
; 3. 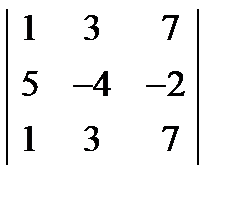 = 0.
= 0.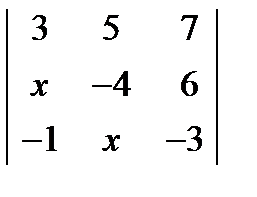 ; 2.
; 2.  ; 3.
; 3. 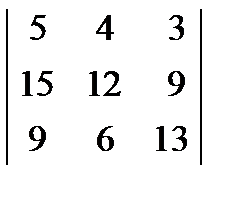 = 0.
= 0.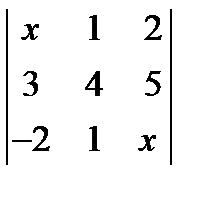 ; 2.
; 2.  ; 3.
; 3. 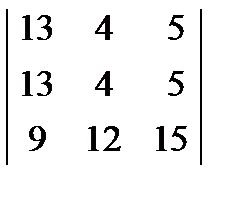 = 0.
= 0.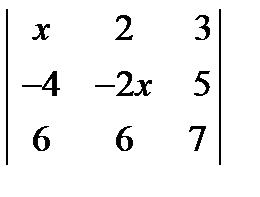 ; 2.
; 2. 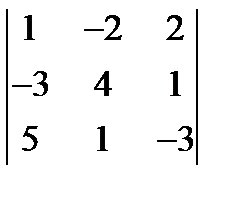 ; 3.
; 3. 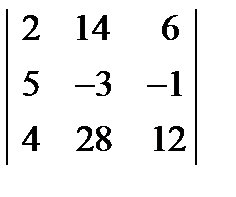 = 0.
= 0.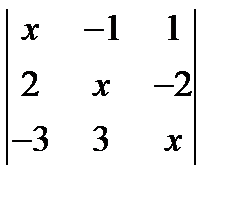 ; 2.
; 2. 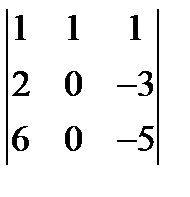 ; 3.
; 3. 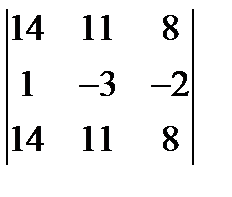 = 0.
= 0.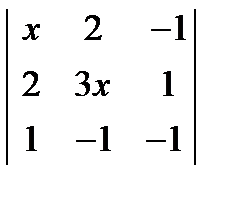 ; 2.
; 2. 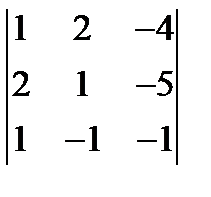 ; 3.
; 3. 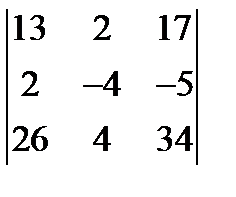 = 0.
= 0.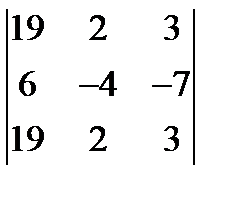 = 0.
= 0.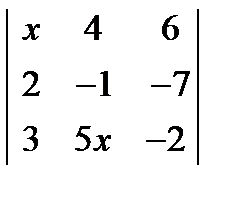 ; 2.
; 2. 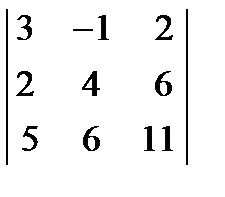 ; 3.
; 3. 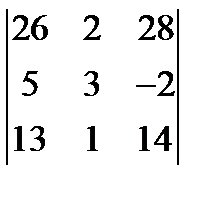 = 0.
= 0.


