Предел функции на бесконечности

Цель:

        - сформировать навыки вычисления пределов на бесконечности;

        - развить умение раскрывать неопределённости вида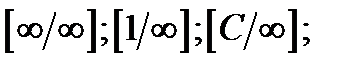

        - закрепить знания о способах деления многочлена на многочлен;

Материально – техническое обеспечение: методические указания по выполнению работы;

Время выполнения: 2 академических часа;

Ход занятия:

1. Изучить краткие теоретические сведения;

2. Выполнить задания;

3. Сделать вывод по работе;

4. Подготовить защиту работы по контрольным вопросам.

 Краткие теоретические сведения:

Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим.

Определение 1: Число А называется пределом функции f(x) при х → ∞, если для любого положительного ε > 0, можно найти такое М > 0, что при всех х, удовлетворяющих неравенству х > М выполняется неравенство | f(x) -А| < ε. Обозначение:

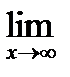f(x) = А, если х_n → ∞ при f(x_n) →А.

Справедливы аналогичные теоремы:

Теорема 1. 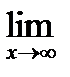 (f(x) ± g(x)) =  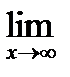f(x) ±  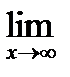g(x).

Теорема 2. 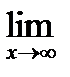 (f(x) · g(x)) =  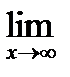f(x) · 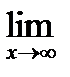g(x).

Следствие 1. 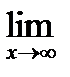 (С∙f(x)) = С ∙ 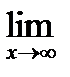f(x).          

Следствие 2. 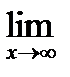 С = С.    

Определение 2: Функция называется бесконечно малой, если её предел при х→ а равен нулю и бесконечно большой, если её предел при х→ а равен бесконечности, т.е. если 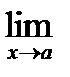f(x) = 0, то f(x) - бесконечно малая и если 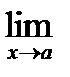f(x) = ∞, то f(x) - бесконечно большая.

    Свойства бесконечно малых:

· Сумма конечного числа бесконечно малых функций — бесконечно малая функция.

· Произведение бесконечно малых функций — бесконечно малая функция.

· Произведение бесконечно малой функции на ограниченную — бесконечно малая функция. Как следствие, произведение бесконечно малой функции на константу — бесконечно малая функция.

· Если f( x)— бесконечно малая функция, сохраняющая знак, то 1/f( x)— бесконечно большая функция.

Рассмотрим часто встречающиеся методы вычисления пределов функций на бесконечности.

Пример 1. Найти предел функции: ;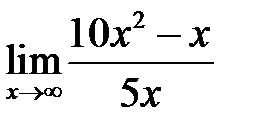

Решение:

При 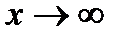 данная функция представляет собой частное двух бесконечно больших величин, имеем неопределенность вида [ 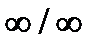]. Чтобы раскрыть эту неопределенность, применим первую предельную теорему и разделим каждое слагаемое числителя на 5х. Тогда получим:

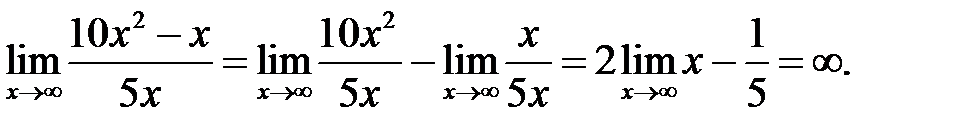
Пример 2. Вычислить предел: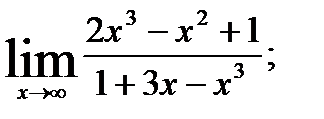

Решение:

При 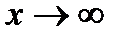 имеем неопределенность вида [ 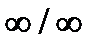]. Чтобы раскрыть эту неопределенность, разделим числитель и знаменатель на  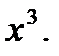Тогда получим:

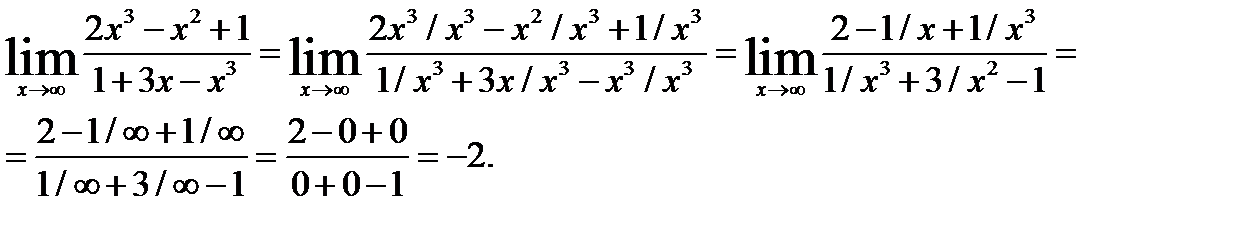
   Пример 3. Вычислить предел: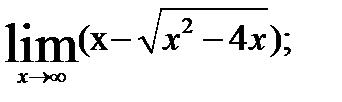

Решение:

При 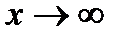 данная функция представляет собой разность двух бесконечно больших величин, имеем неопределённость вида [ 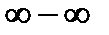]. Раскроем неопределённость, умножив и разделив функцию на сопряжённое выражение

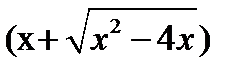, и при помощи элементарных преобразований получим:

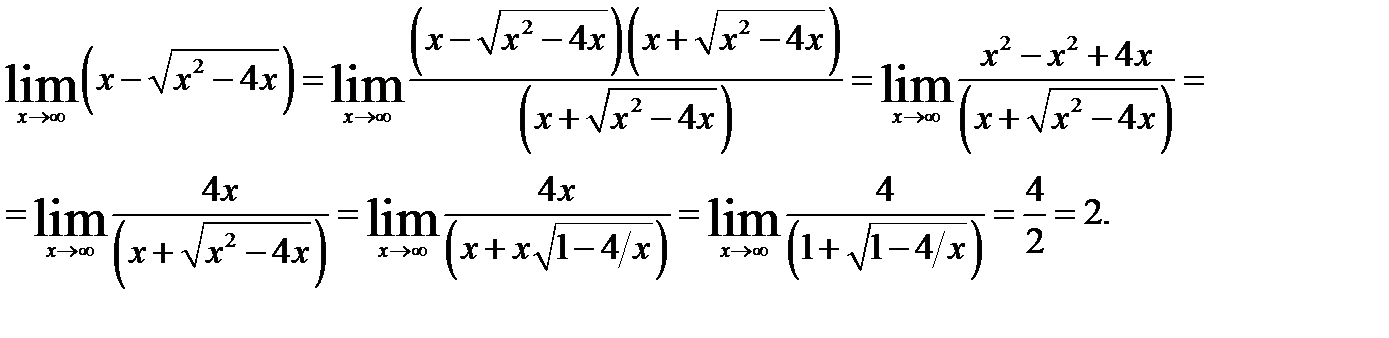
Задание для самостоятельного выполнения:

Найти пределы функций на бесконечности.

Вариант 1.

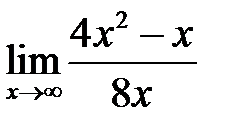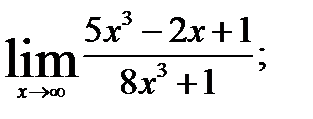1. ;            2.              3.

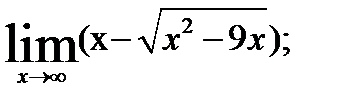
Вариант 2.

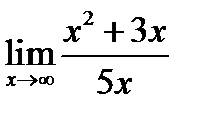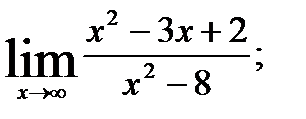1. ;           2.                 3.

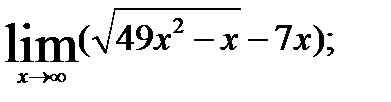
Вариант 3.

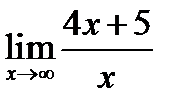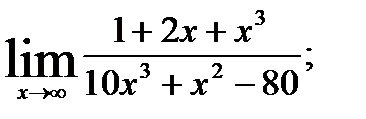1. ;           2.            3.

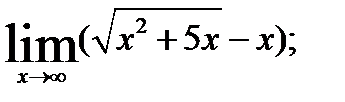
Вариант 4.

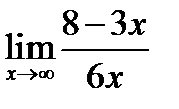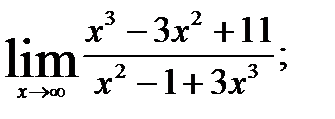1. ;           2.               3.

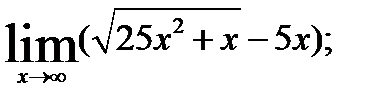
Вариант 5.

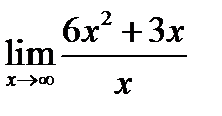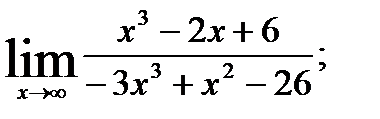1. ;           2.           3.

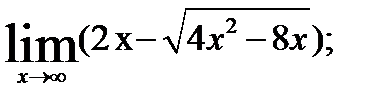
Вариант 6.

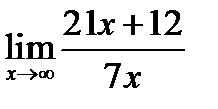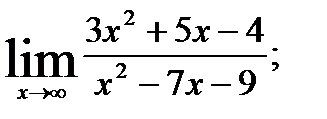1. ;      2.               3.

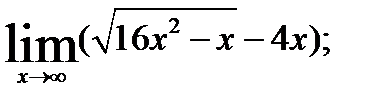
Вариант 7.

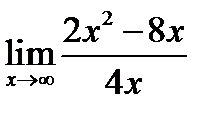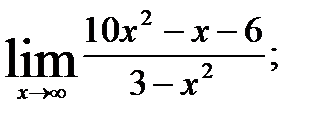1. ;          2.               3.

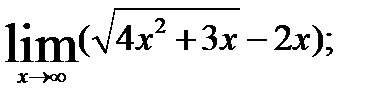
Вариант 8.

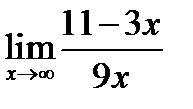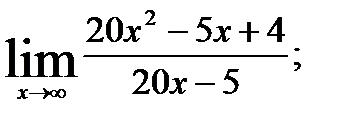1. ;      2.             3.

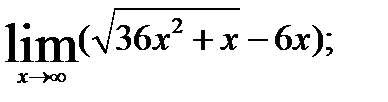
Вариант 9.

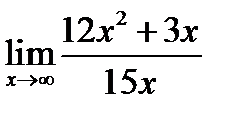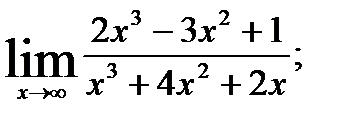1. ;        2.             3.  

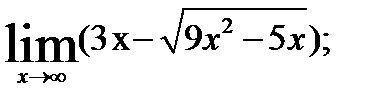
Вариант 10.

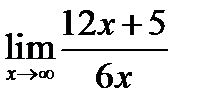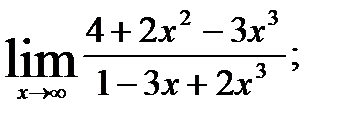1. ;      2.              3.  

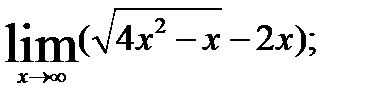
Вариант 11.

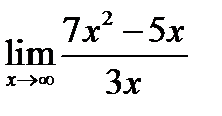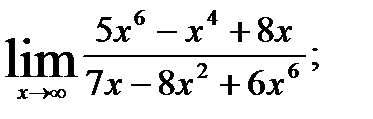1. ;           2.            3.

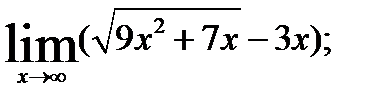
Вариант 12.

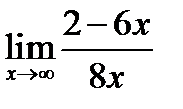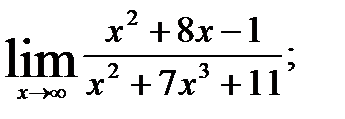1. ;         2.              3.

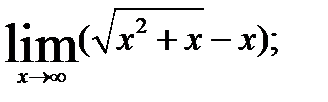
Вариант 13.

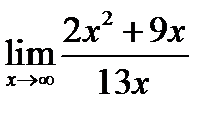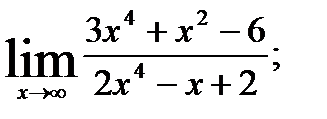1. ;       2.               3.

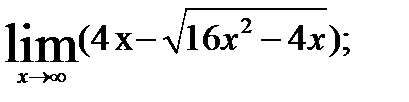
Вариант 14.

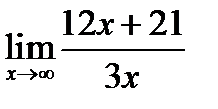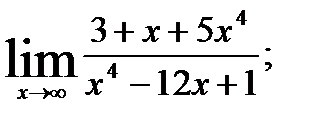1. ;     2.                3.  

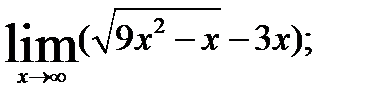
Вариант 15.

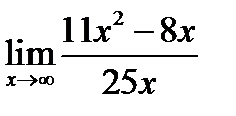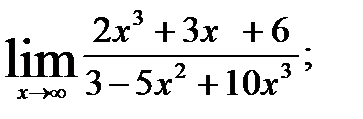1. ;         2.            3.

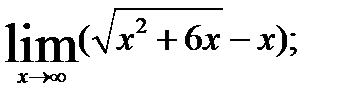
Вопросы для самоконтроля:

1. Перечислите основные методы вычисления пределов на бесконечности.

2. Сформулируйте теоремы о пределах.

3. Какая функция является бесконечно малой, бесконечно большой?

4. Назовите свойства бесконечно малых.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 9