Исследование функции и построение графика

Цель:

- сформировать навыки исследования функций по первой и второй производной;

        - развить способность применения результатов исследования к построению графика функции;

        - закрепить знания о наибольшем и наименьшем значениях функции;

   Материально – техническое обеспечение: методические указания по выполнению работы, стенды «Правила дифференцирования».

Время выполнения: 2 академических часа;

Ход занятия:

1. Изучить краткие теоретические сведения;

2. Выполнить задания;

3. Сделать вывод по работе;

4. Подготовить защиту работы по контрольным вопросам.

Краткие теоретические сведения:

Исследование функции на монотонность и экстремум.

Возрастающие и убывающие функции называют монотонными, а промежутки, в которых функция возрастает или убывает,- промежутками монотонности. Возрастание и убывание функции y = f( x) характеризуется знаком её первой производной:

- если в некотором промежутке первая производная f ´( x) >0, то функция возрастает в этом промежутке;

- если в некотором промежутке первая производная f ´( x) <0, то функция убывает в этом промежутке.

Точки минимума и максимума функции называются точками экстремума функции. Ими являются только критические точки, т.е. точки, в которых производная равна нулю или терпит разрыв. Если при переходе через критическую точку х₀ производная f ´( x) меняет знак, то функция y = f( x) имеет в точке х₀

экстремум:

~ максимум (max), если производная 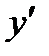 меняет знак с “+” на “-“;  

~ минимум (min), если производная 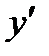 меняет знак с “-“ на “+”;

~ если знак 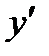 не меняется, то функция не имеет экстремума в данной точке.

Алгоритм исследования функции на монотонность и экстремум:

1. Найти производную функции .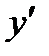

2. Приравнять 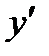 к нулю, решить уравнение, найти критические точки.

3. Исключить критические точки из области определения 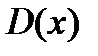, указать интервалы знакопостоянства .

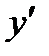4. На каждом интервале определить знак производной .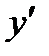

5. По знаку производной 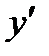 установить монотонность функции на интервалах:

при 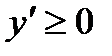 функция y = f( x) возрастает ↑, при  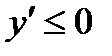функция убывает ↓.

6. Найти экстремумы функций, исследуя знак производной 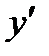 в окрестности каждой критической точки.

7. Вычислить значения экстремумов в критических точках.

8. Результаты исследования занести в таблицу.

9. Построить схематический график данной функции.

Пример 1. Исследовать функцию 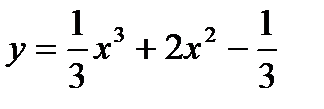  на монотонность и экстремум.

Решение:

1)

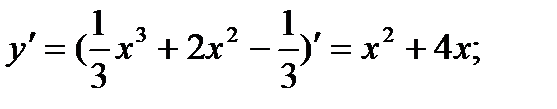
2) х²+4х=0; х(х+4)=0; х₁=0 или х₂=-4                                          

3)  

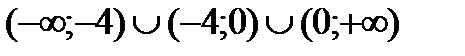
4) ;

;

               

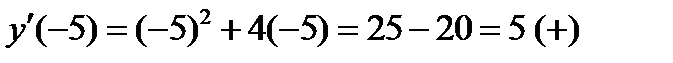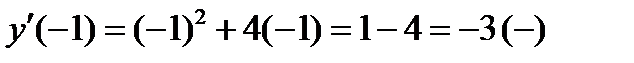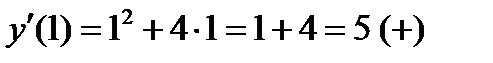
        +     -      +     f ’(x)              

               -4     0             

5) ,

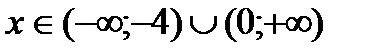
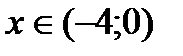
6)           max   min          

        +     -      +     f ’(x)              

               -4     0             

7) .

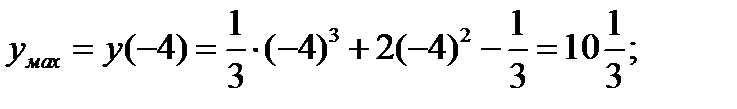
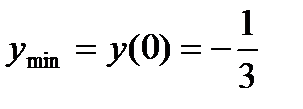8) Результаты исследования:

х		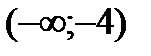-4	(-4;0)	0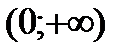
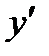
	+	0	-	0	+
у		max	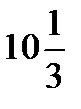	min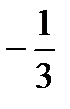

 

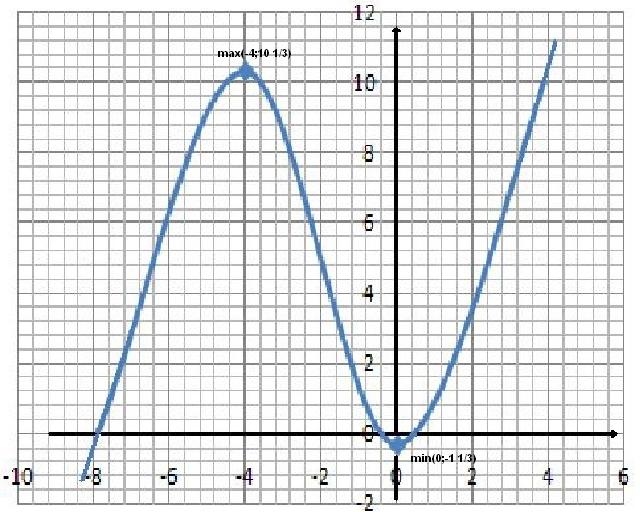
9) График функции 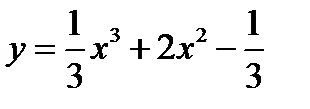 изображён на рис.1