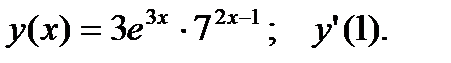Цель:
- сформировать навыки нахождения производных тригонометрических функций;
- развить умение вычисления значения производной при заданном значении аргумента;
- закрепить знания о способах дифференцирования сложной функции;
Материально – техническое обеспечение: методические указания по выполнению работы, стенды «Правила дифференцирования», таблица значений тригонометрических функций;
Время выполнения: 2 академических часа;
Ход занятия:
1. Изучить краткие теоретические сведения;
2. Выполнить задания;
3. Сделать вывод по работе;
4. Подготовить защиту работы по контрольным вопросам.
Краткие теоретические сведения:
Производные тригонометрических функций находят по правилам:
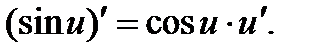
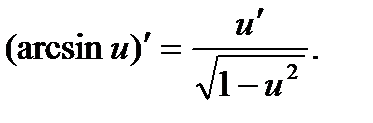
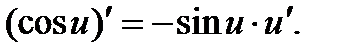
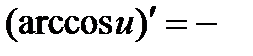
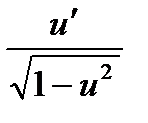 .
.
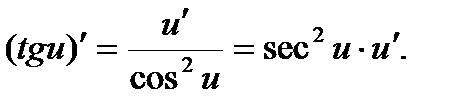
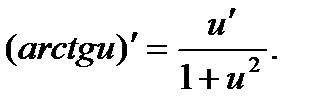
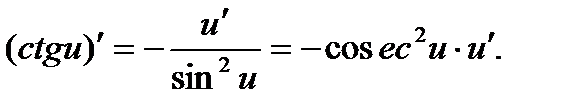
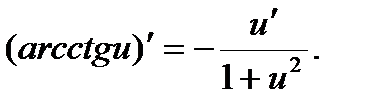
Пример 1. Найти производную функции y=sin 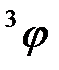 и вычислить ее значение при
и вычислить ее значение при 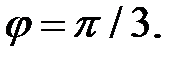
Решение. Это сложная функция с промежуточным аргументом sin 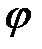 .
.
Дифференцируем её по формулам 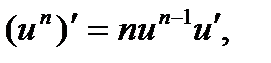
 :
:
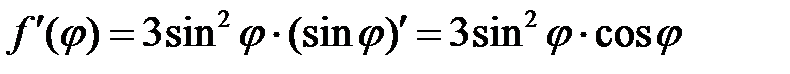
Вычислим значение производной при 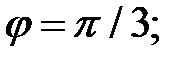
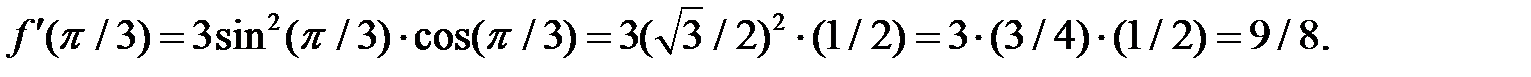
Пример 2. Найти производную функций при данном значении аргумента:
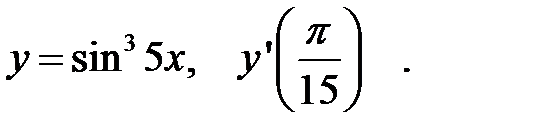
Решение:
Используя формулы: 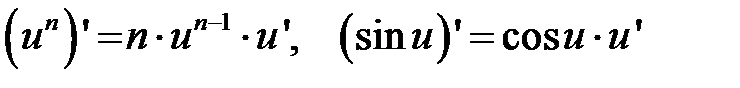 , найдем производную:
, найдем производную:
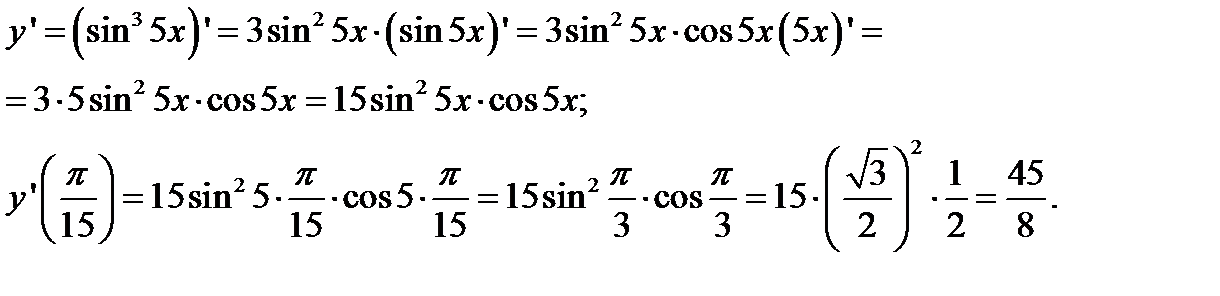
Пример 3. Найти производную функции f ( x)=  .
.
Решение. Сначала преобразуем функцию, используя свойства логарифмов:
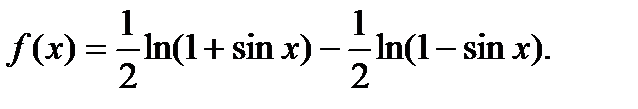
Дифференцируя, получим:
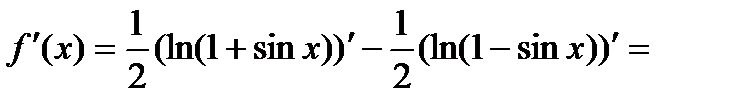
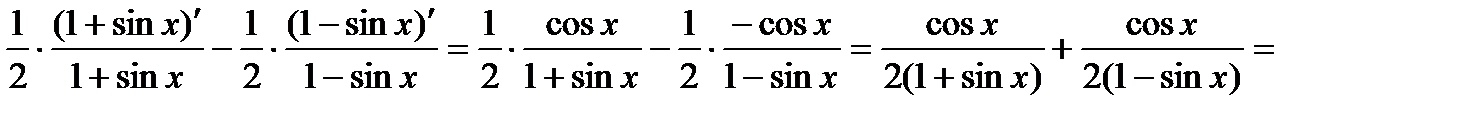
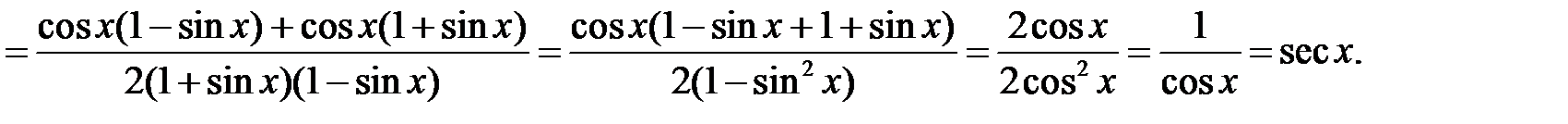
Задания для самостоятельного выполнения:
Найти производные функций при данном значении аргумента.
Вариант 1.
1. 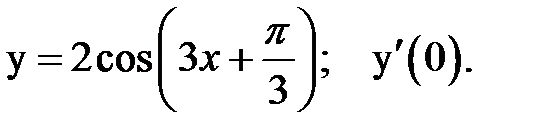 2.
2. 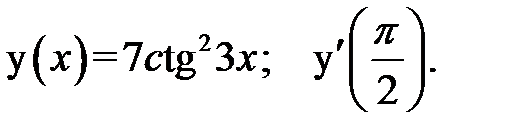
3. 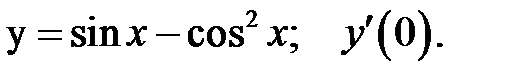 4.
4. 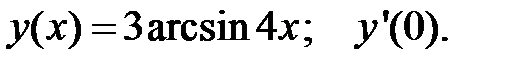
Вариант 2.
1. 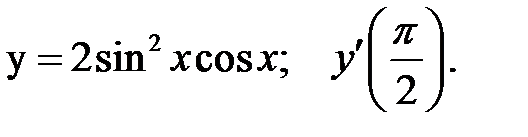 2.
2. 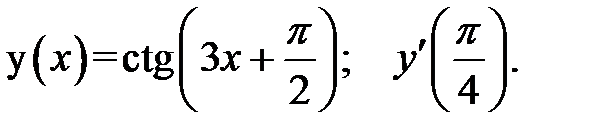
3. 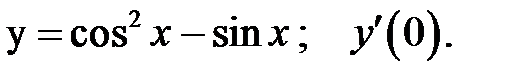 4.
4. 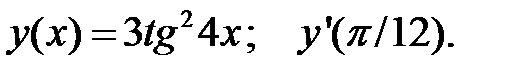
Вариант 3.
1. 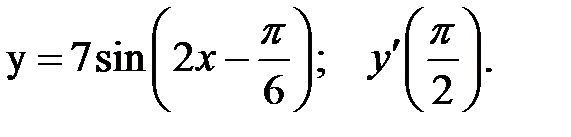 2.
2. 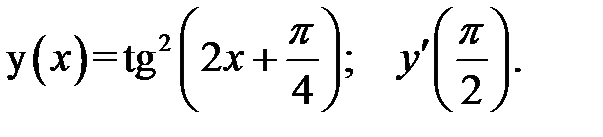
3. 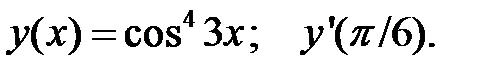 4.
4. 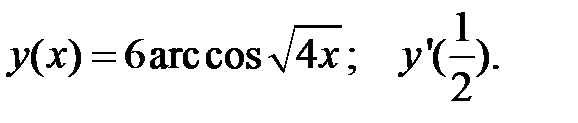
Вариант 4.
1. 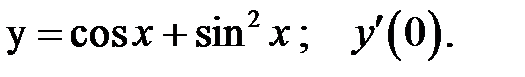 2.
2. 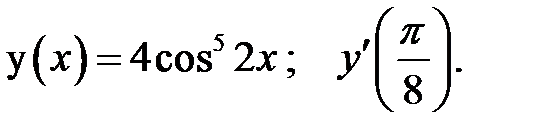
3. 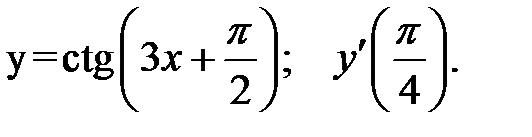 4.
4. 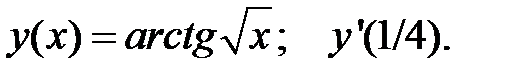
Вариант 5.
1. 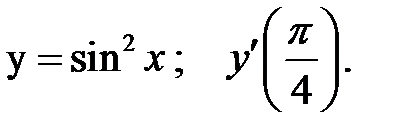 2.
2. 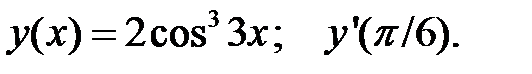
3. 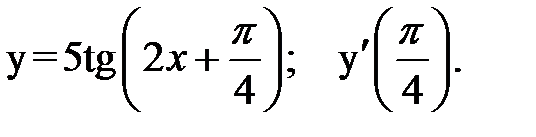 4.
4. 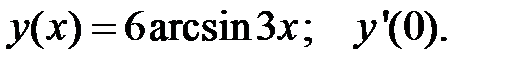
Вариант 6.
1. 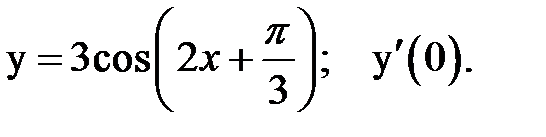 2.
2. 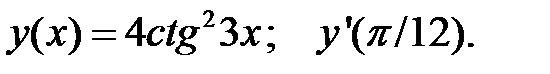
3. 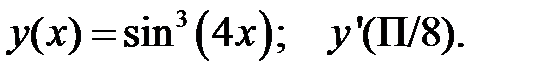 4.
4. 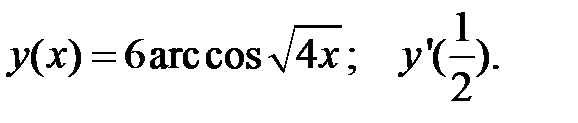
Вариант 7.
1. 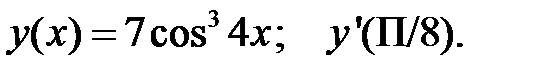 2.
2. 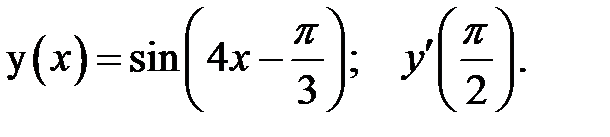
3. 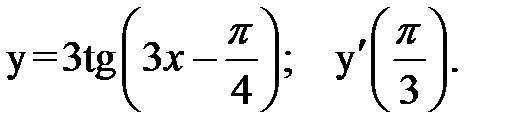 4.
4. 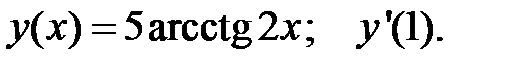
Вариант 8.
1. 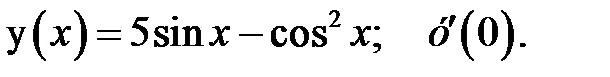 2.
2. 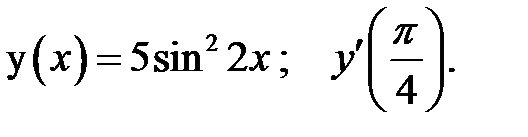
3. 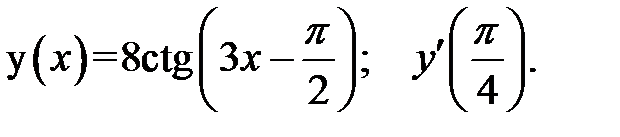 4.
4. 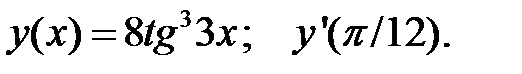
Вариант 9.
1. 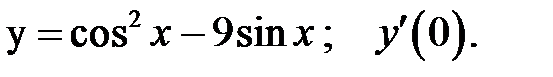 2.
2. 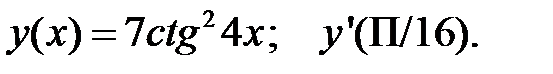
3. 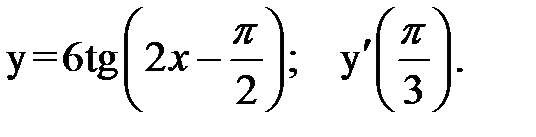 4.
4. 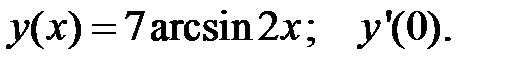
Вариант 10.
1. 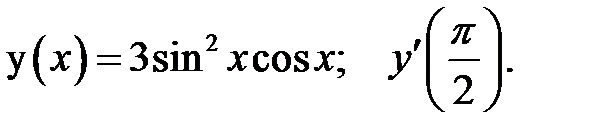 2.
2. 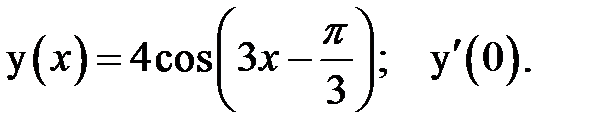
3.  4.
4. 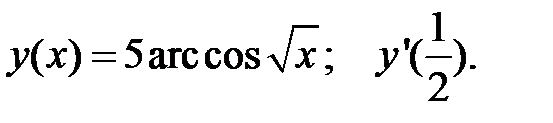
Вариант 11.
1. 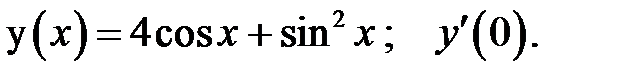 2.
2. 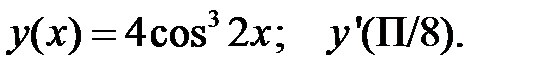
3. 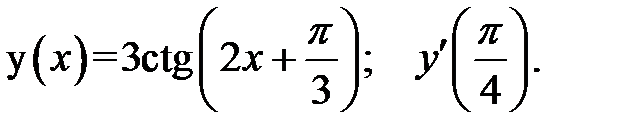 4.
4. 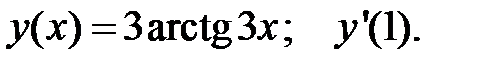
Вариант 12.
1. 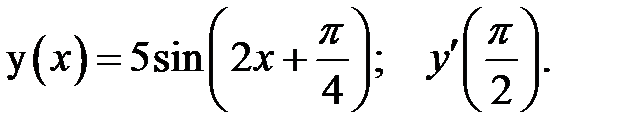 2.
2. 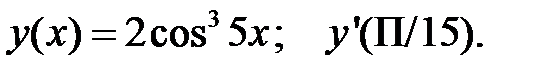
3. 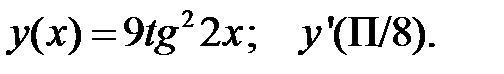 4.
4. 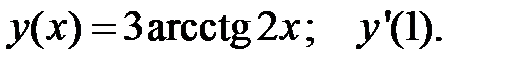
Вариант 13.
1. 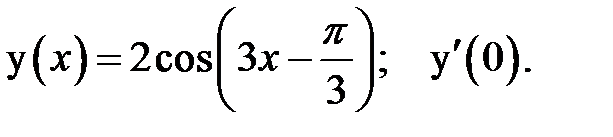 2.
2. 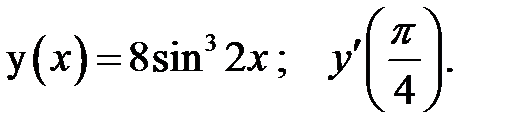
3. 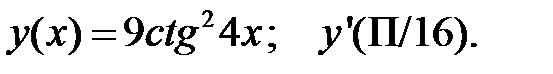 4.
4. 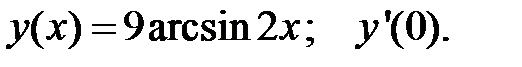
Вариант 14.
1. 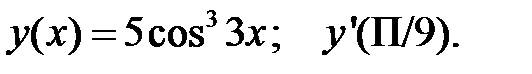 2.
2. 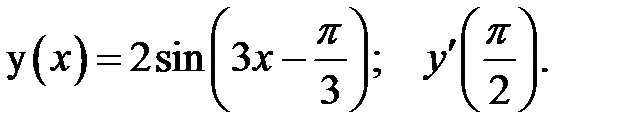
3. 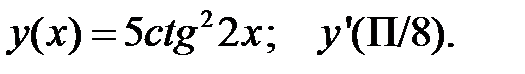 4.
4. 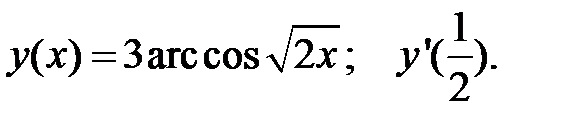
Вариант 15.
1. 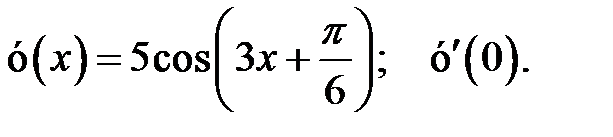 2.
2. 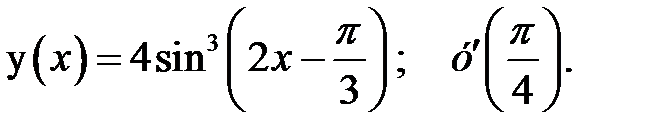
3. 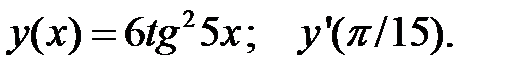 4.
4. 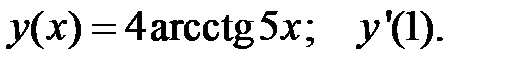
Вопросы для самоконтроля:
1. Чему равны производные синуса и косинуса?
2. Чему равны производные тангенса и котангенса?
3. Запишите формулы производных обратных тригонометрических функций.
4. Как найти производную сложной тригонометрической функции?
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 12
ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКИХ И
ПОКАЗАТЕЛЬНЫХ ФУНКЦИЙ
Цель:
- сформировать навыки нахождения производных логарифмических и показательных функций;
- развить умение вычисления значения производной при заданном значении аргумента;
- закрепить знания о способах дифференцирования сложной функции;
Материально – техническое обеспечение: методические указания по выполнению работы, стенды «Правила дифференцирования», «Свойства логарифмов», таблица значений тригонометрических функций;
Время выполнения: 2 академических часа;
Ход занятия:
1. Изучить краткие теоретические сведения;
2. Выполнить задания;
3. Сделать вывод по работе;
4. Подготовить защиту работы по контрольным вопросам.
Краткие теоретические сведения:
Производные логарифмических и показательных функций находят по правилам:
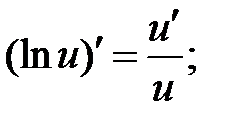
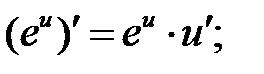
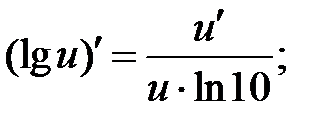
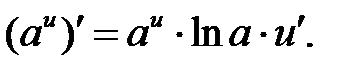
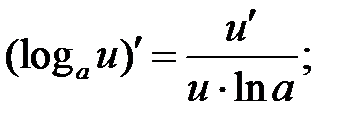
Пример 1. Найти производную функции 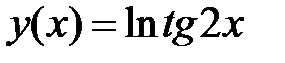 и вычислить значение
и вычислить значение 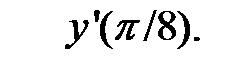
Решение. Используем формулу 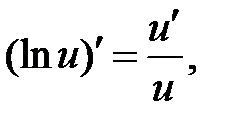 подставим в неё tg2 x вместо u.
подставим в неё tg2 x вместо u.
Получаем, y´( x)= 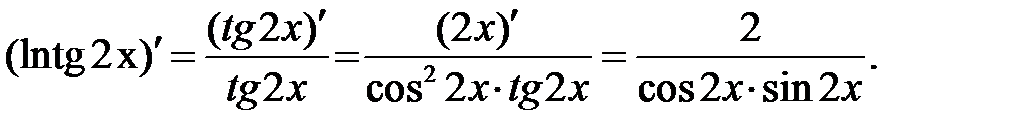
Найдём значение производной в точке х = π∕8:
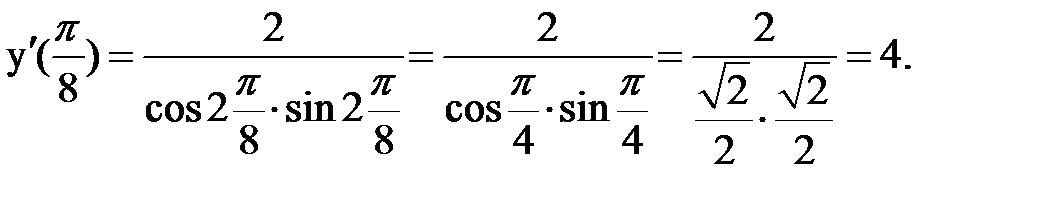
Пример 2. Найти производную функции 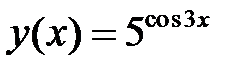 и вычислить значение
и вычислить значение 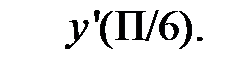
Решение. Используем формулу 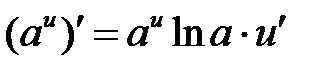 и подставим в неё cos3 x
и подставим в неё cos3 x
вместо u при условии а=5.
Получаем, 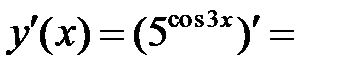
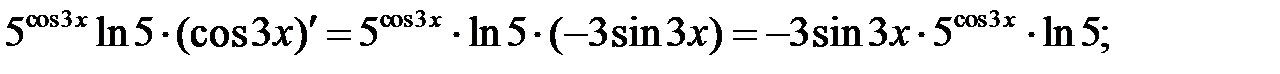
Найдём значение производной в точке х = π∕6:
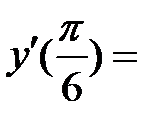
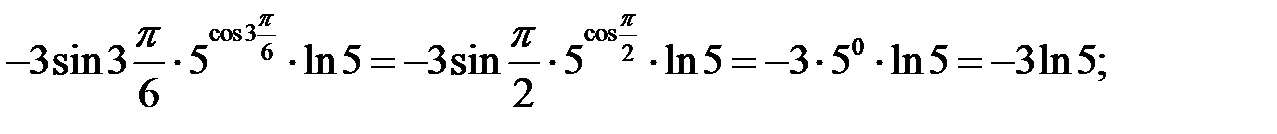
Пример 3. Найти производную функции 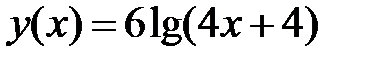 и вычислить значение
и вычислить значение 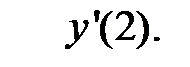
Решение. Используем формулу 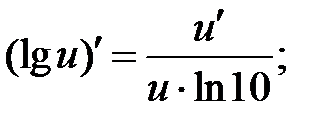 и подставим в неё 4 x+4
и подставим в неё 4 x+4
вместо u.
Получаем, y´( x)= 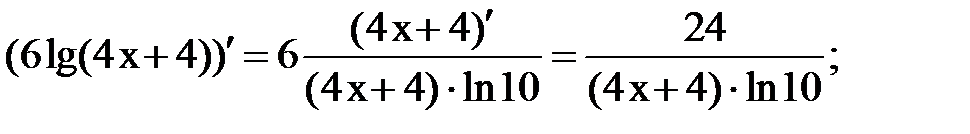
Найдём значение производной в точке х = 2:
y´(2)= 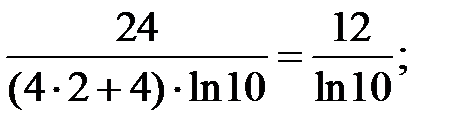
Пример 4. Найти производную функции 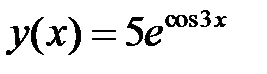 и вычислить значение
и вычислить значение 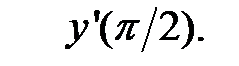
Решение. Используем формулу 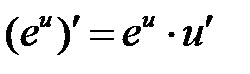 и подставим в неё cos3 x
и подставим в неё cos3 x
вместо u.
Получаем,
y´( x) = 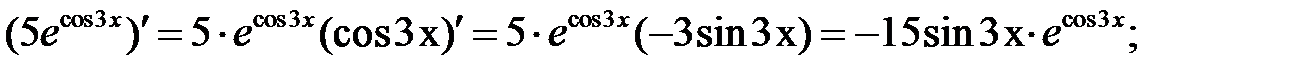
Найдём значение производной в точке х = π ∕2:
y´( π ∕2)= 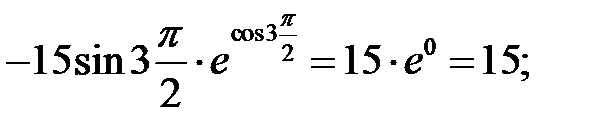
Задания для самостоятельного выполнения:
Найти производные функций при данном значении аргумента.
Вариант 1.
1. 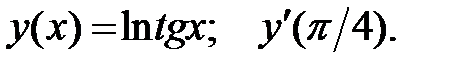 2.
2. 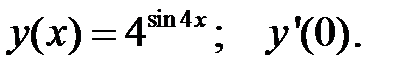
3. 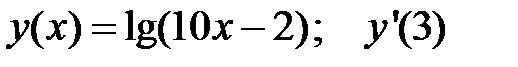 . 4.
. 4. 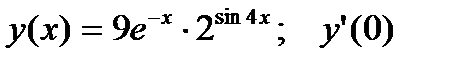 .
.
Вариант 2.
1. 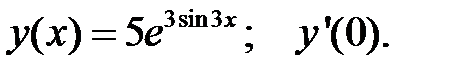 2.
2. 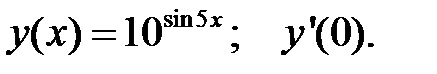
3. 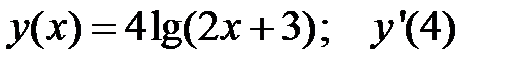 4.
4. 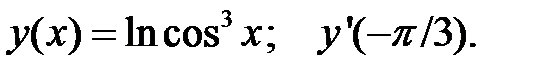
Вариант 3.
1. 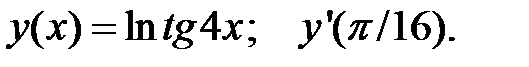 2.
2. 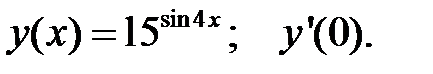
3. 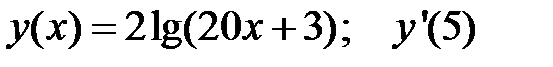 4.
4. 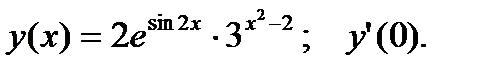
Вариант 4.
1. 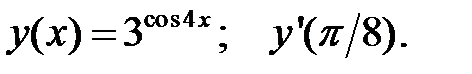 2.
2. 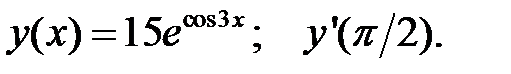
3. 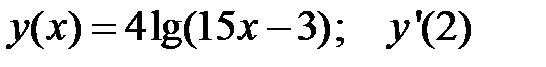 4.
4. 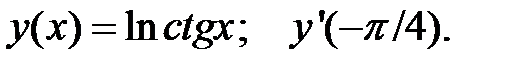
Вариант 5.
1. 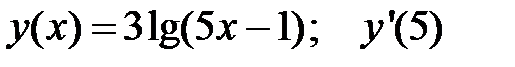 2.
2. 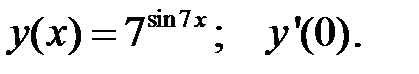
3. 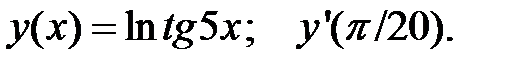 4.
4. 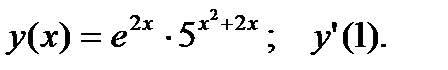
Вариант 6.
1. 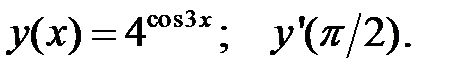 2.
2. 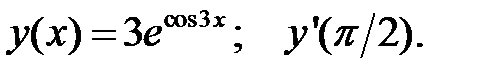
3. 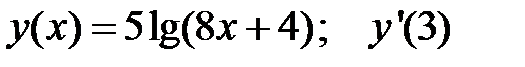 4.
4. 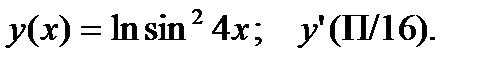
Вариант 7.
1. 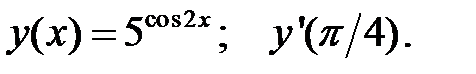 2.
2. 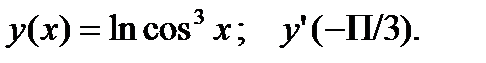
3. 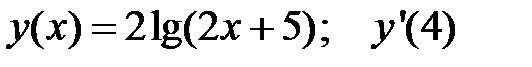 4.
4. 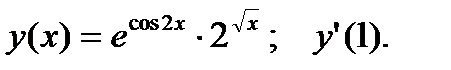
Вариант 8.
1. 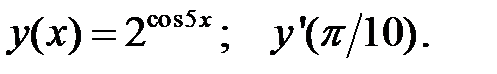 2.
2. 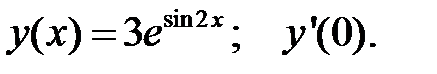
3. 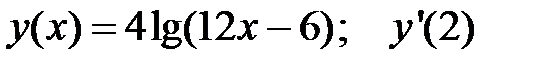 4.
4. 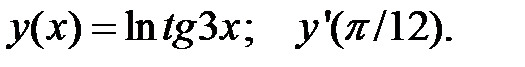
Вариант 9.
1. 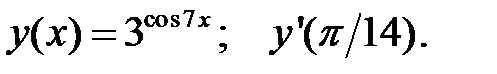 2.
2. 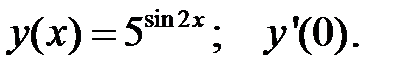
3. 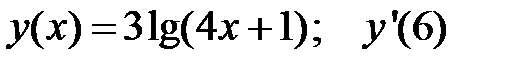 4.
4. 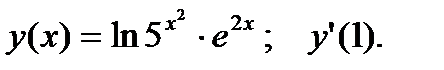
Вариант 10.
1. 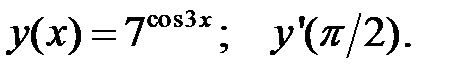 2.
2. 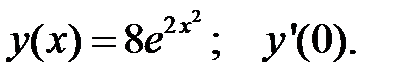
3. 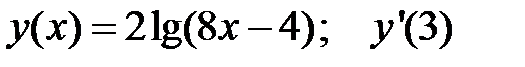 4.
4. 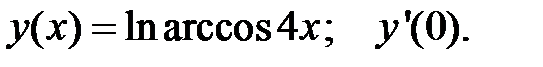
Вариант 11.
1. 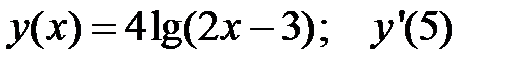 2.
2. 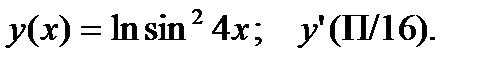
3. 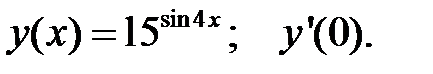 4.
4. 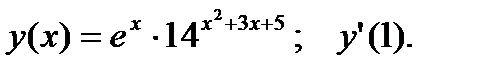
Вариант 12.
1. 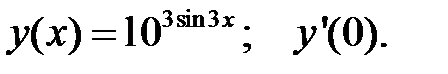 2.
2. 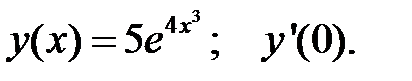
3. 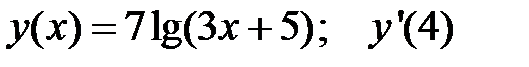 4.
4. 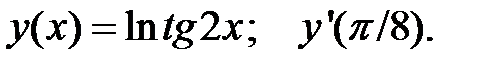
Вариант 13.
1. 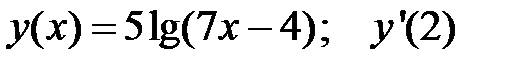 2.
2. 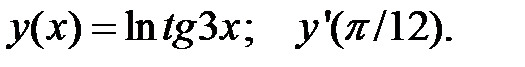
3. 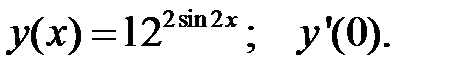 4.
4. 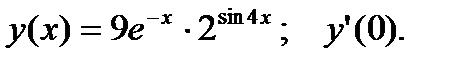
Вариант 14.
1. 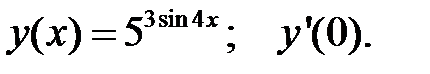 2.
2. 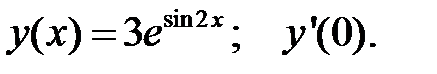
3. 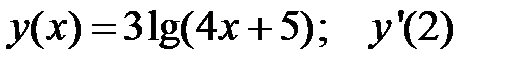 4.
4. 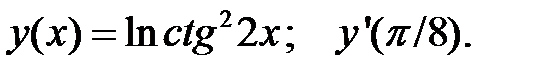
Вариант 15.
1. 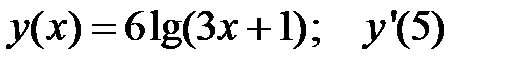 2.
2. 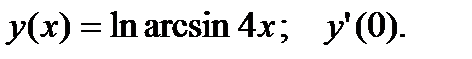
3. 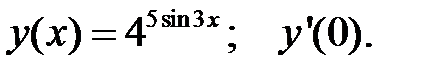 4.
4. 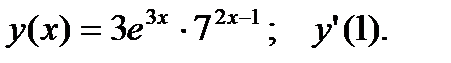
Вопросы для самоконтроля:
1. Чему равна производная натурального логарифма?
2. Запишите формулу производной десятичного логарифма.
3. Чему равна производная экспоненциальной функции?
4. Как найти производную показательной функции с основанием а?
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 13





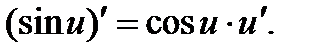
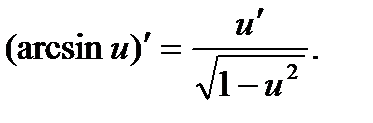
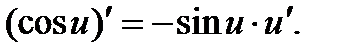
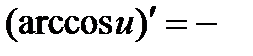
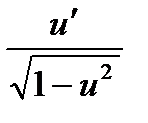 .
.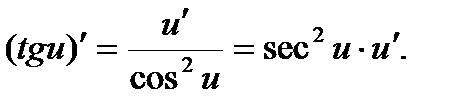
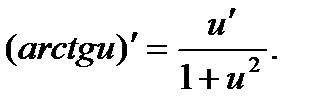
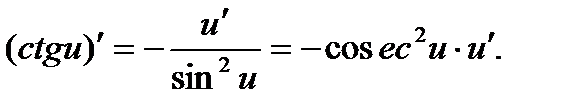
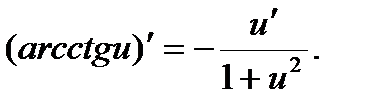
 и вычислить ее значение при
и вычислить ее значение при 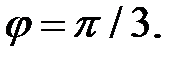
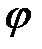 .
.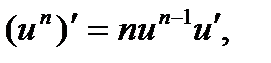
 :
: 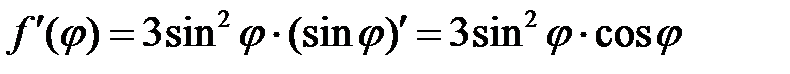
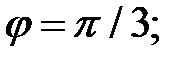
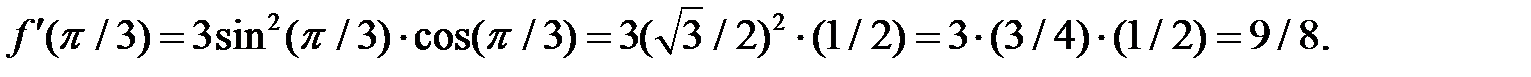
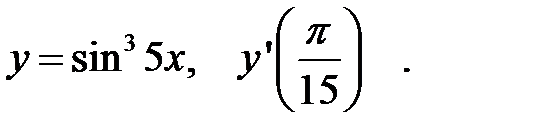
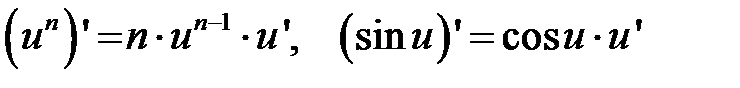 , найдем производную:
, найдем производную: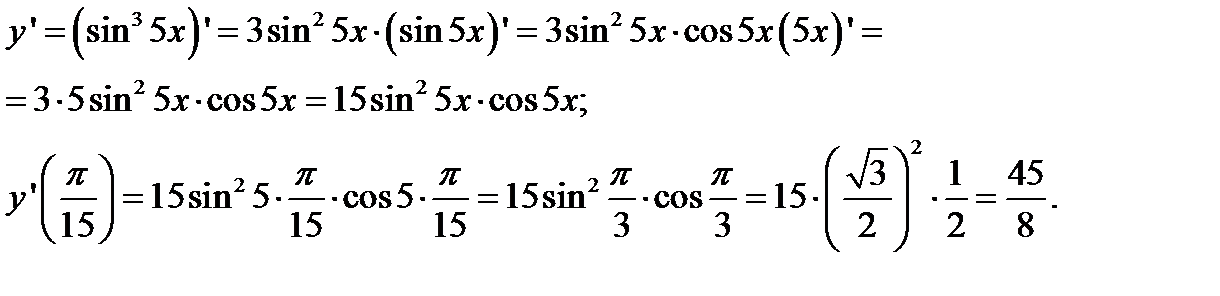
 .
. 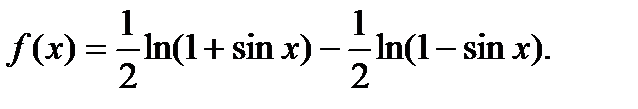
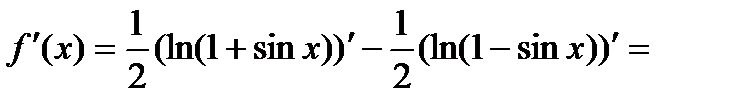
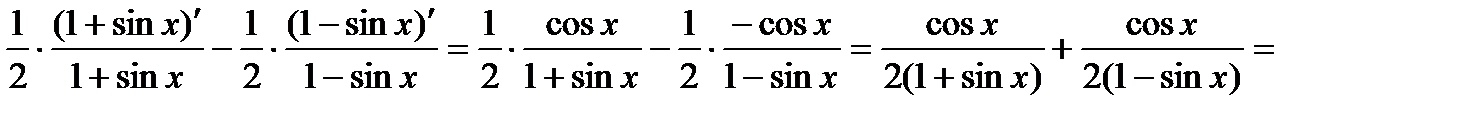
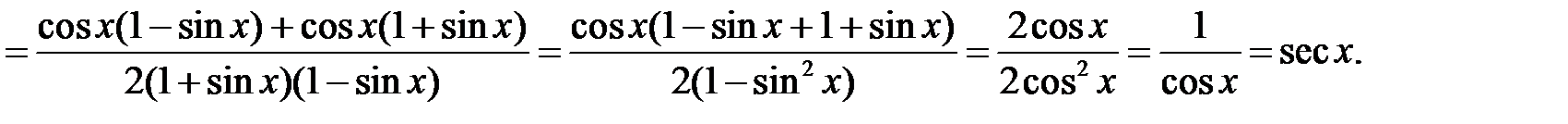
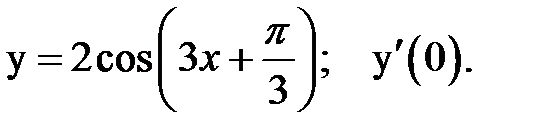 2.
2. 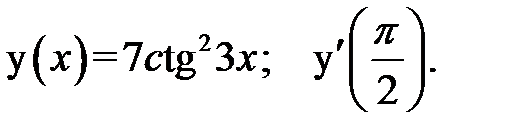
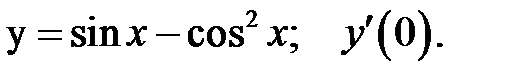 4.
4. 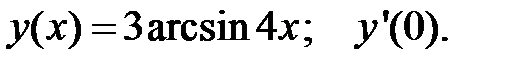
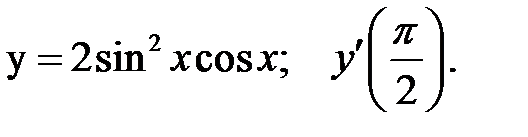 2.
2. 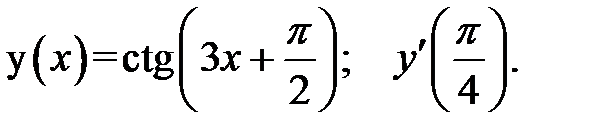
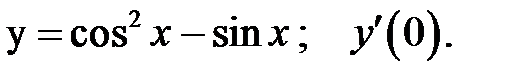 4.
4. 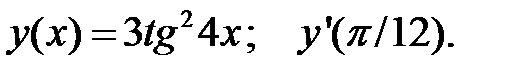
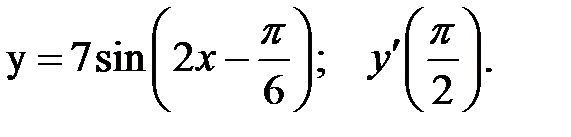 2.
2. 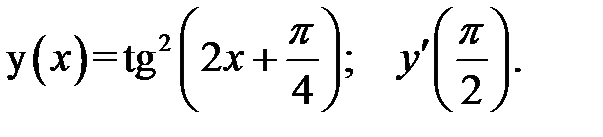
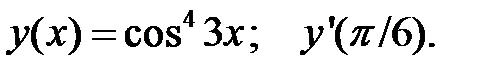 4.
4. 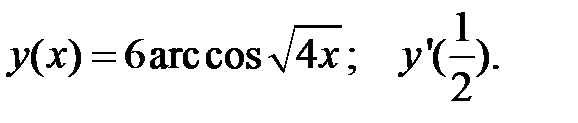
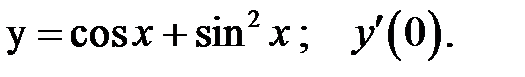 2.
2. 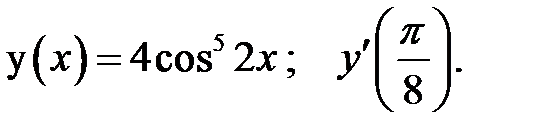
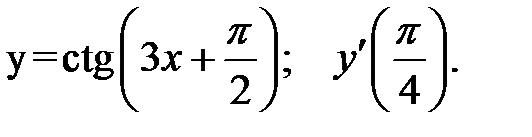 4.
4. 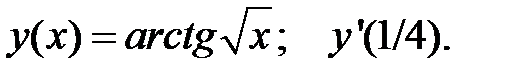
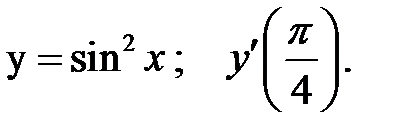 2.
2. 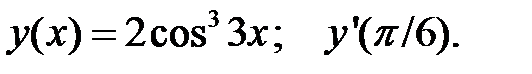
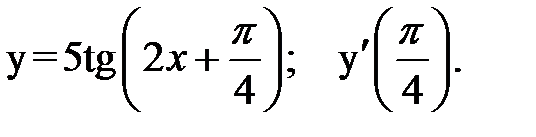 4.
4. 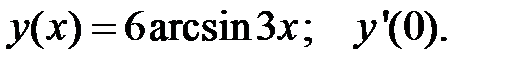
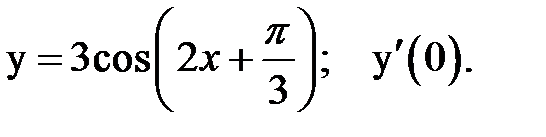 2.
2. 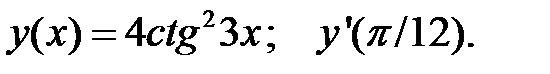
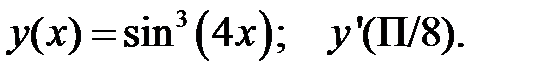 4.
4. 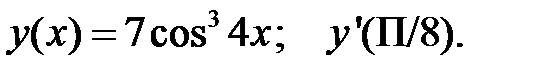 2.
2. 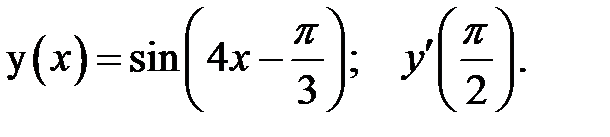
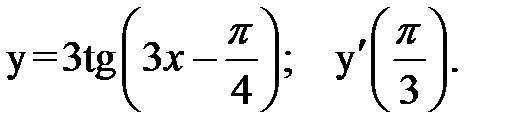 4.
4. 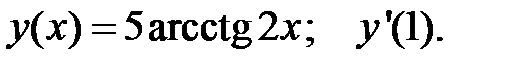
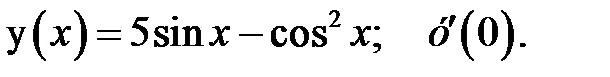 2.
2. 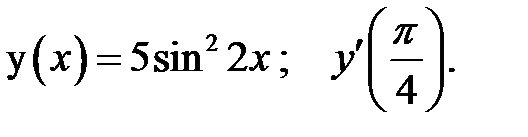
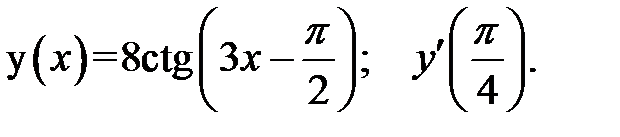 4.
4. 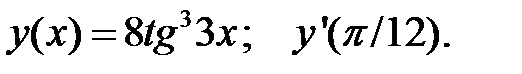
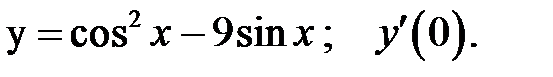 2.
2. 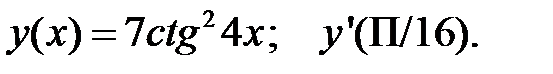
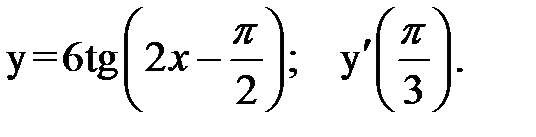 4.
4. 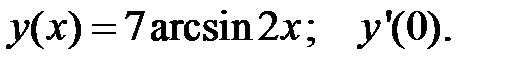
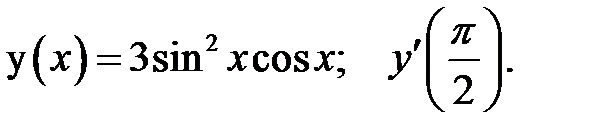 2.
2. 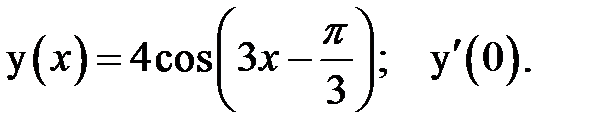
 4.
4. 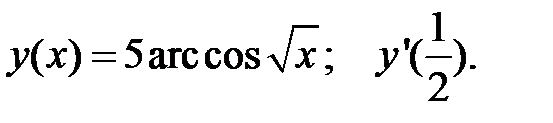
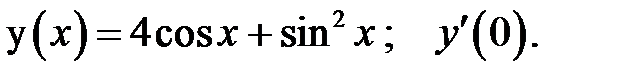 2.
2. 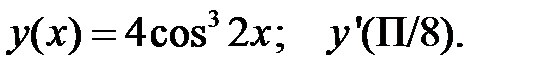
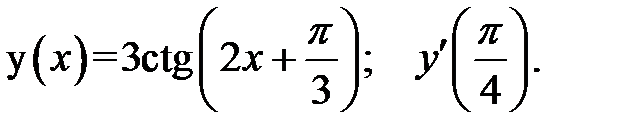 4.
4. 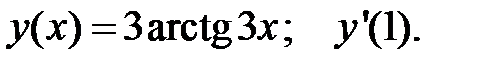
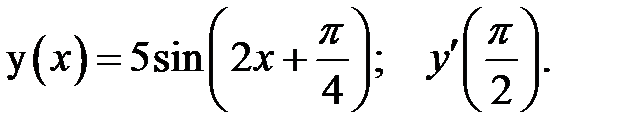 2.
2. 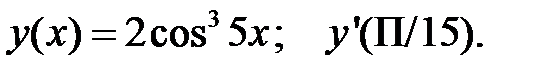
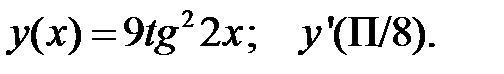 4.
4. 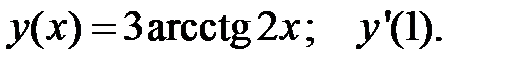
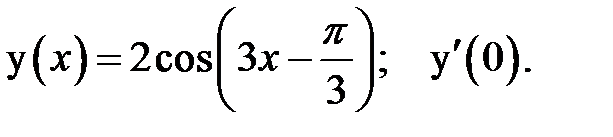 2.
2. 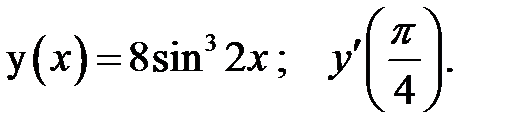
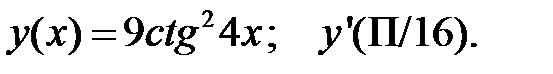 4.
4. 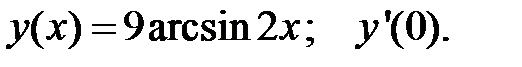
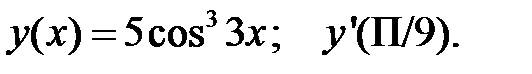 2.
2. 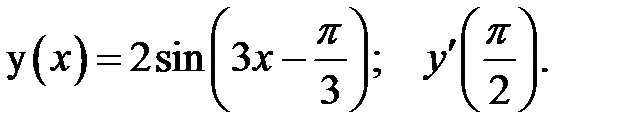
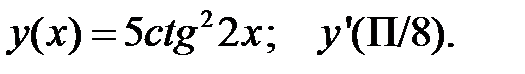 4.
4. 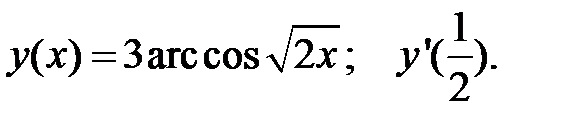
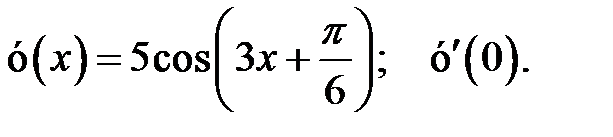 2.
2. 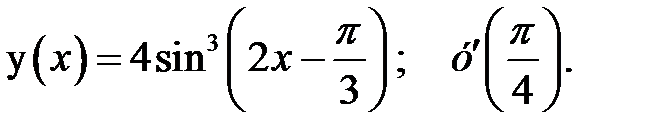
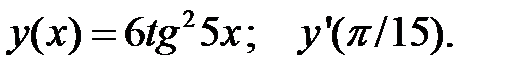 4.
4. 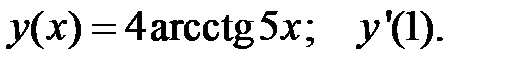
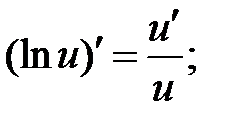
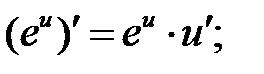
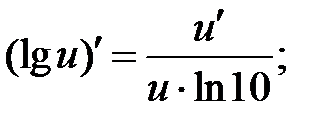
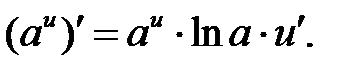
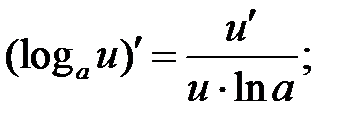
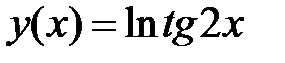 и вычислить значение
и вычислить значение 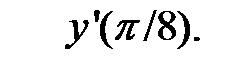
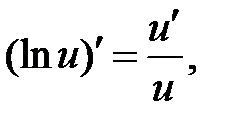 подставим в неё tg2 x вместо u.
подставим в неё tg2 x вместо u.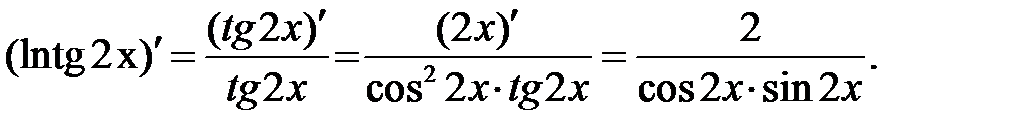
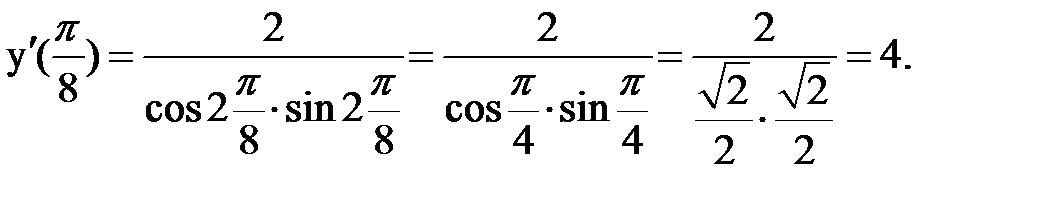
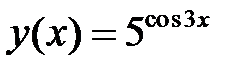 и вычислить значение
и вычислить значение 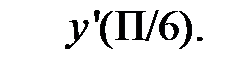
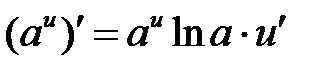 и подставим в неё cos3 x
и подставим в неё cos3 x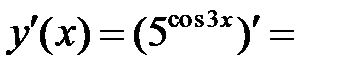
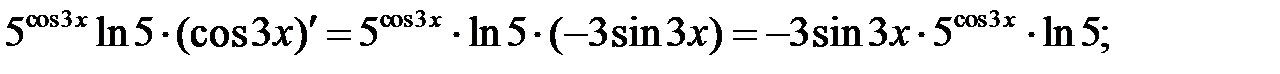
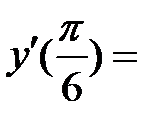
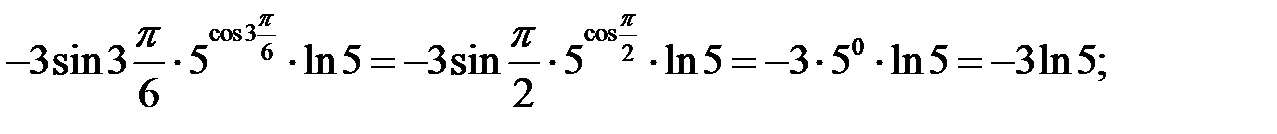
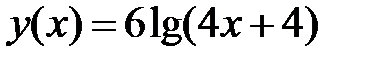 и вычислить значение
и вычислить значение 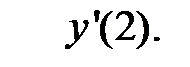
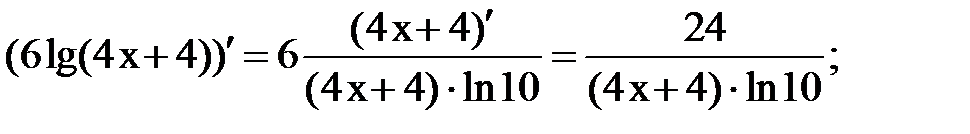
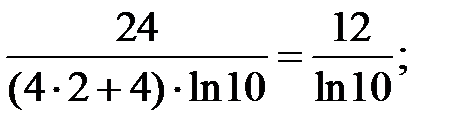
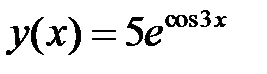 и вычислить значение
и вычислить значение 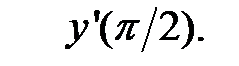
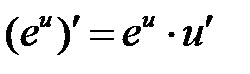 и подставим в неё cos3 x
и подставим в неё cos3 x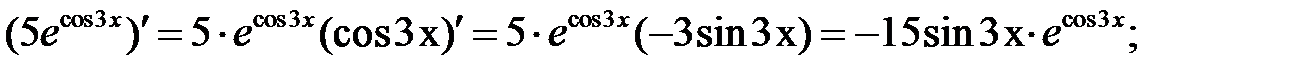
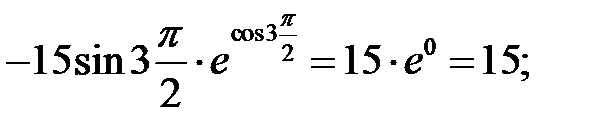
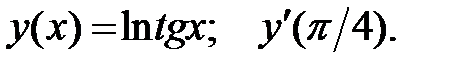 2.
2. 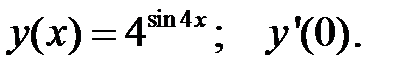
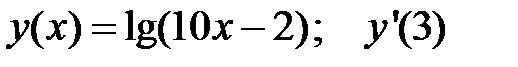 . 4.
. 4. 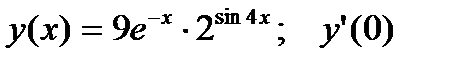 .
.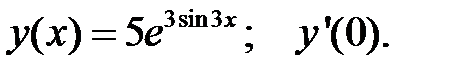 2.
2. 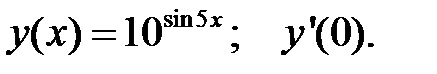
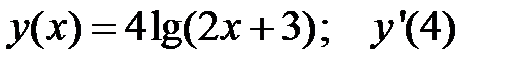 4.
4. 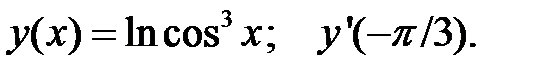
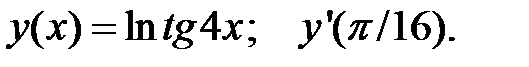 2.
2. 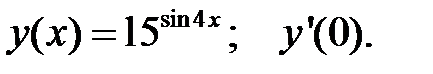
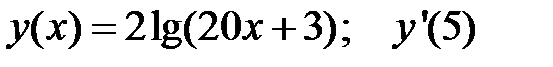 4.
4. 
 2.
2. 
 4.
4. 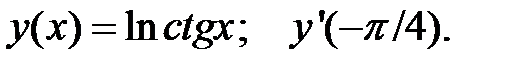
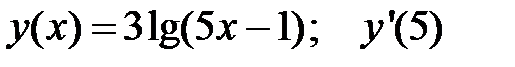 2.
2. 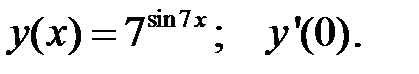
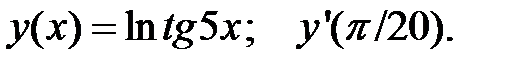 4.
4. 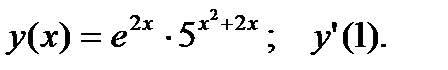
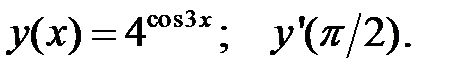 2.
2. 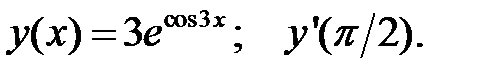
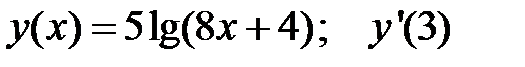 4.
4. 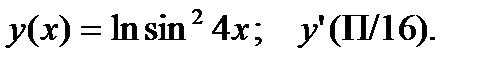
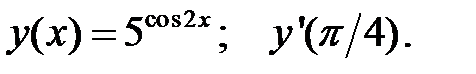 2.
2. 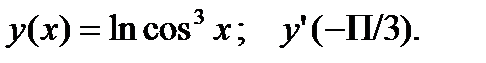
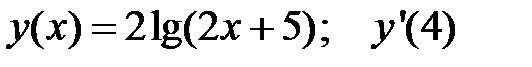 4.
4. 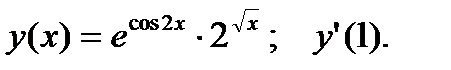
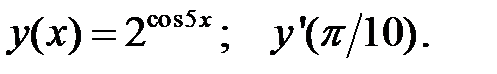 2.
2. 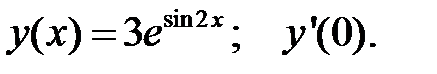
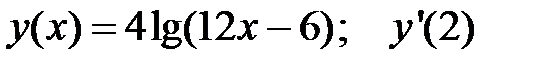 4.
4. 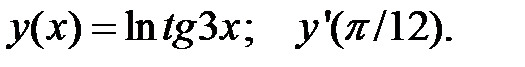
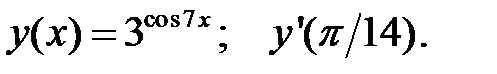 2.
2. 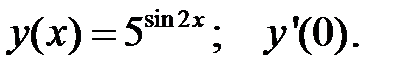
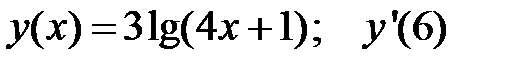 4.
4. 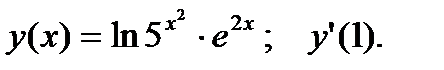
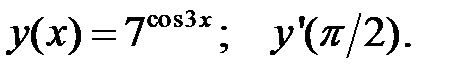 2.
2. 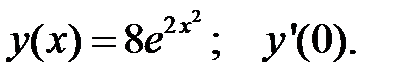
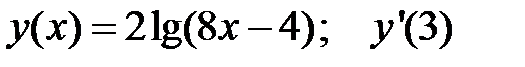 4.
4. 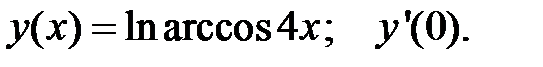
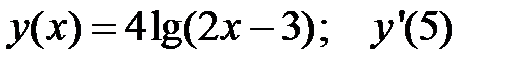 2.
2. 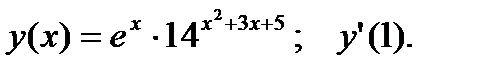
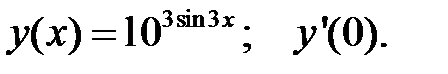 2.
2. 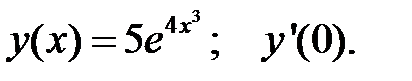
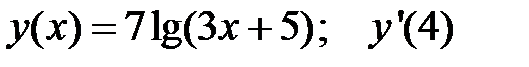 4.
4. 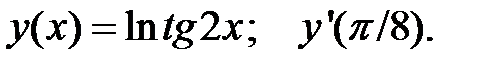
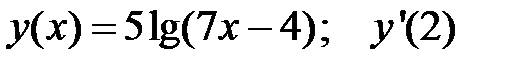 2.
2. 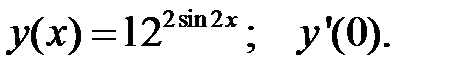 4.
4. 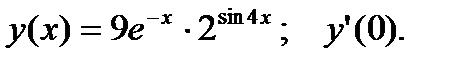
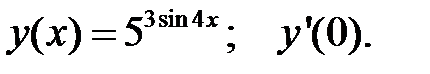 2.
2. 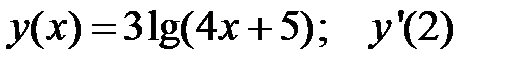 4.
4. 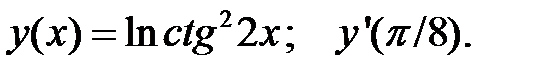
 2.
2. 
 4.
4.