Цель:
- сформировать навыки нахождения производных функций по правилам дифференцирования суммы и разности, произведения и частного;
- развить умение вычисления значения производной при заданном значении аргумента;
- закрепить знания о способах преобразования степенных выражений;
Материально – техническое обеспечение: методические указания по выполнению работы, стенды «Правила дифференцирования»;
Время выполнения: 2 академических часа;
Ход занятия:
1. Изучить краткие теоретические сведения;
2. Выполнить задания;
3. Сделать вывод по работе;
4. Подготовить защиту работы по контрольным вопросам.
Краткие теоретические сведения:
Производной функции y= f( x) в точке х0 называется предел отношения приращения функции Δ f к приращению аргумента Δх, когда последнее стремится к нулю:
y′ = f′( x) = 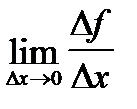 =
=  ;
;
Функция, имеющая конечную производную, называется дифференцируемой.
Операция нахождения производной называется дифференцированием.
Если y= f( x) и u=φ( x) – дифференцируемые функции своих аргументов, то производная сложной функции y= f (φ( x)) существует и равна произведению производной функции y по промежуточному аргументу u на производную промежуточного аргумента u по независимой переменной x:
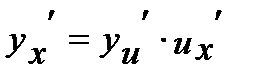 ;
;
Аналогичная формула верна и для сложных функций, которые задаются с помощью цепочки, содержащей три звена и более.
Таблица формул дифференцирования:
1. 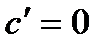 7.
7. 
2. 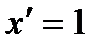 ,
, 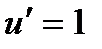 8.
8. 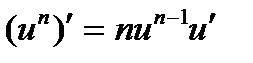
3. 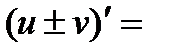
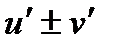 . 9.
. 9. 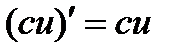 ′.
′.
4. 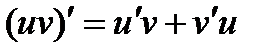 . 10.
. 10. 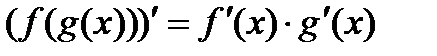
5. 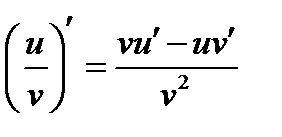 . 11.
. 11. 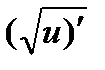 =
= 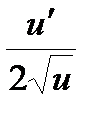 ;
;
6. 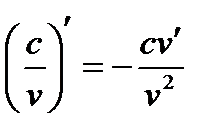 .
.
Здесь u и v - дифференцируемые функции от x, а C – постоянная величина.
Рассмотрим технику вычисления производных функций на примерах.
Пример 1. Найти производную функции при данном значении аргумента:
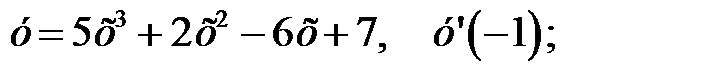
Решение:
1. Применив последовательно правила дифференцирования суммы и степени: 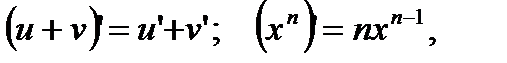 имеем:
имеем: 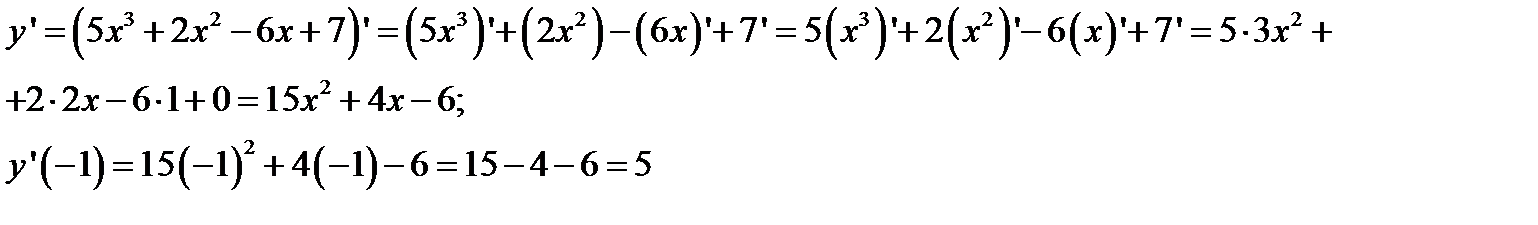
Пример 2. Найти производную функции при данном значении аргумента:
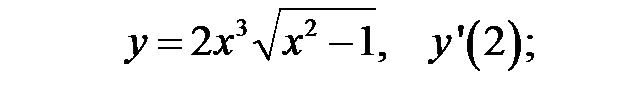
Решение:
Применив правило дифференцирования произведения: 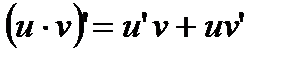 , имеем:
, имеем:
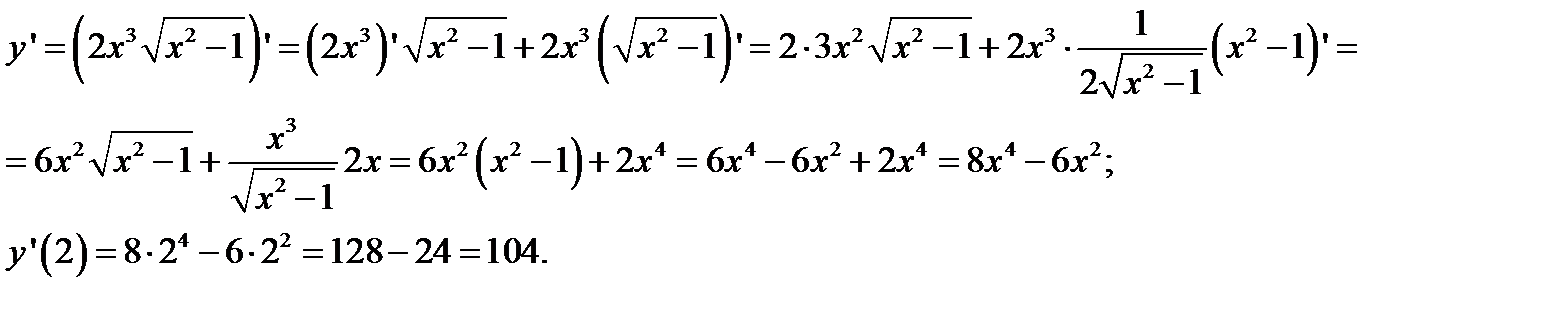
Пример 3. Найти производную функции при данном значении аргумента:
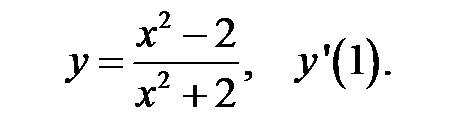
Решение:
Применив правило дифференцирования частного: 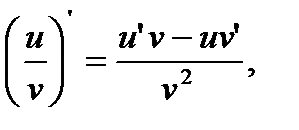 имеем:
имеем:
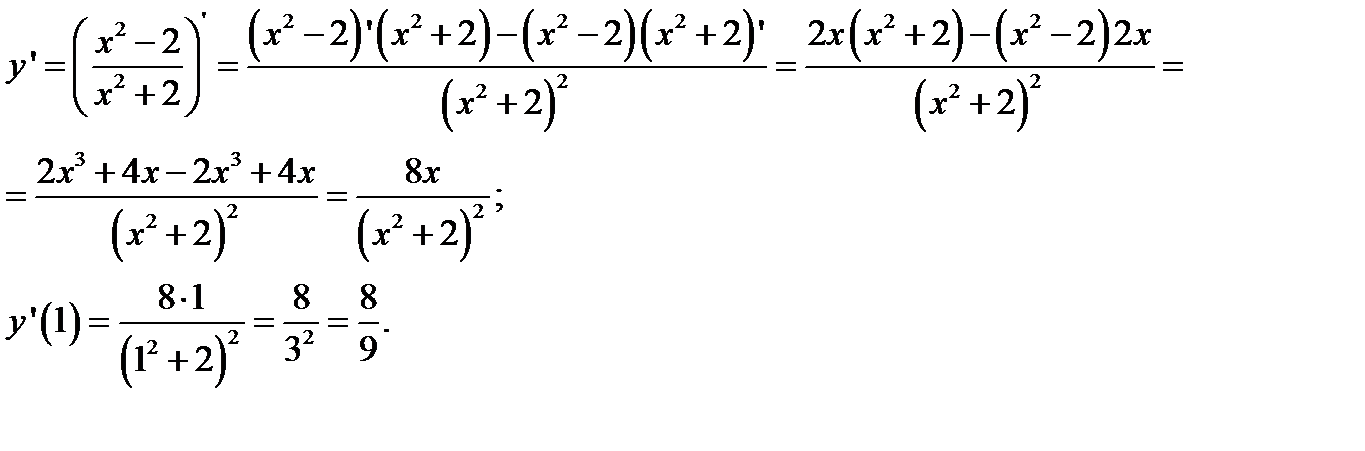
Задание для самостоятельного выполнения:
Найти производные функций при данном значении аргумента.
Вариант 1.
1. 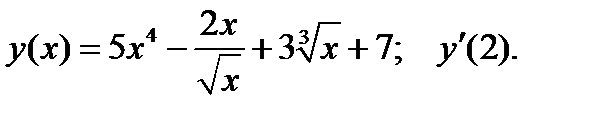 2.
2. 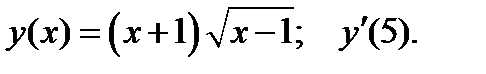
3. 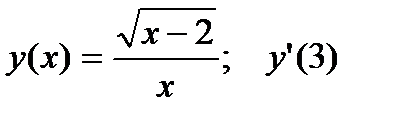 .
.
Вариант 2.
1. 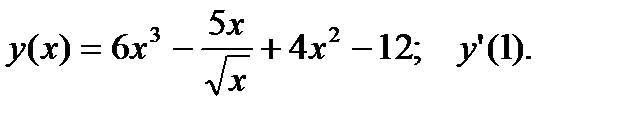 2.
2. 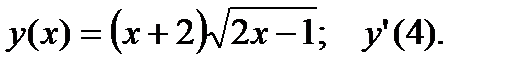
3. 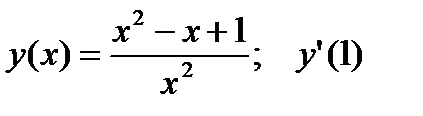 .
.
Вариант 3.
1. 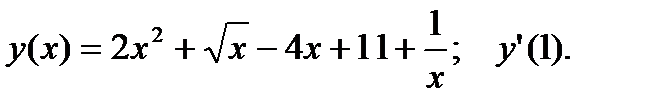 2.
2. 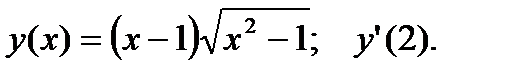
3. 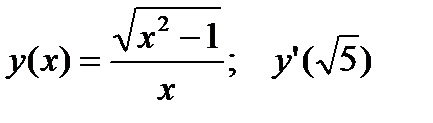 .
.
Вариант 4.
1. 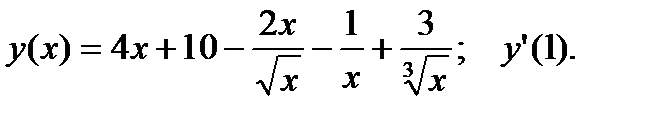 2.
2. 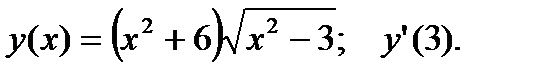
3. 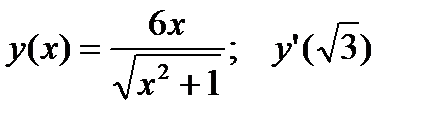 .
.
Вариант 5.
1. 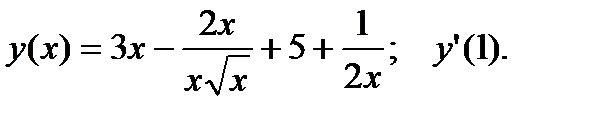 2.
2. 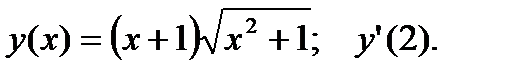
3. 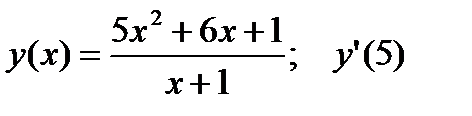
Вариант 6.
1. 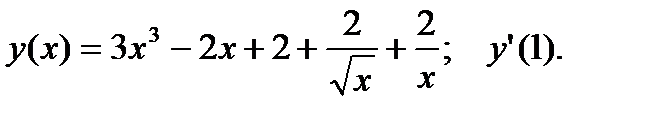 2.
2. 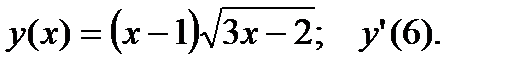
3. 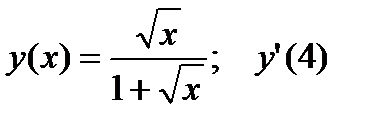 .
.
Вариант 7.
1. 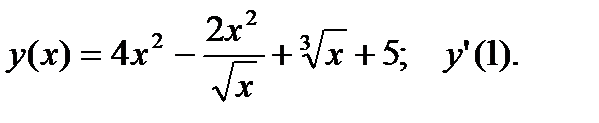 2.
2. 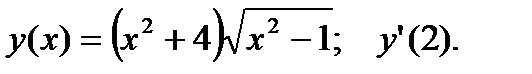
3. 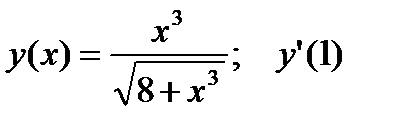 .
.
Вариант 8.
1. 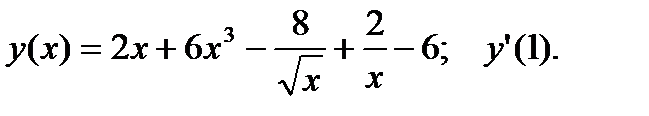 2.
2. 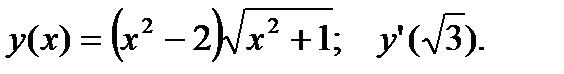
3. 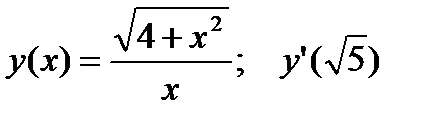 .
.
Вариант 9.
1. 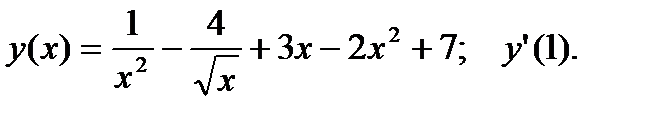 2.
2. 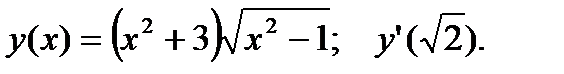
3. 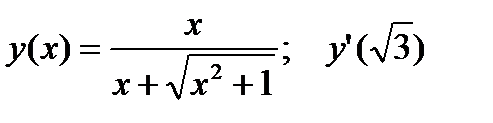 .
.
Вариант 10.
1. 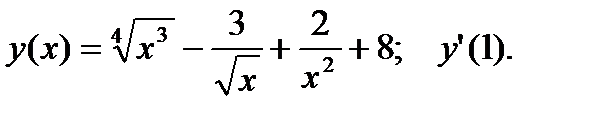 2.
2. 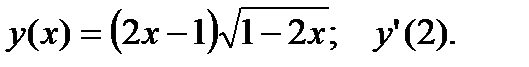
3. 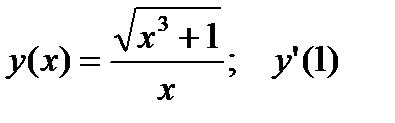 .
.
Вариант 11.
1. 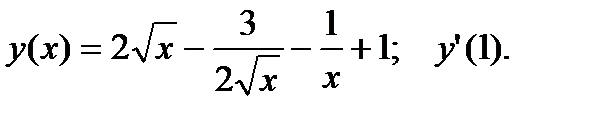 2.
2. 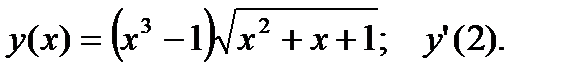
3. 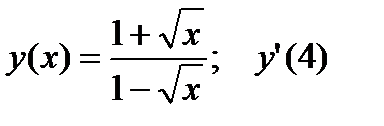 .
.
Вариант 12.
1. 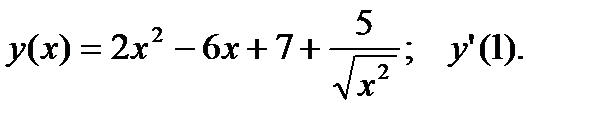 2.
2. 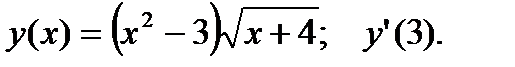
3. 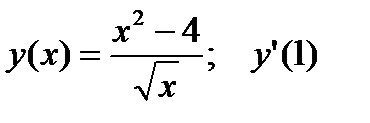 .
.
Вариант 13.
1. 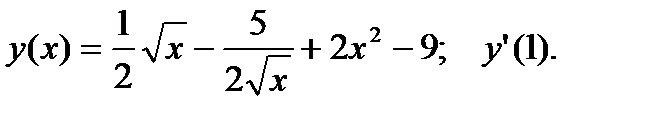 2.
2. 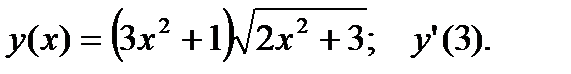
3. 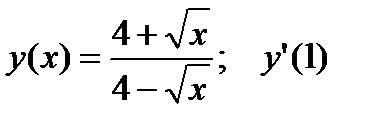 .
.
Вариант 14.
1. 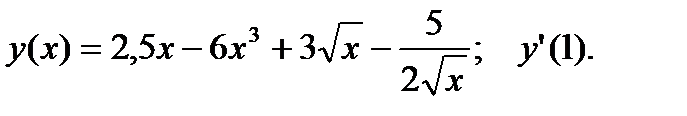 2.
2. 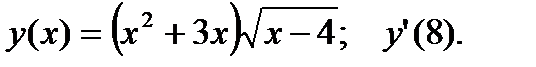
3. 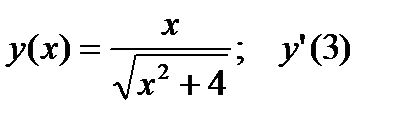 .
.
Вариант 15.
1. 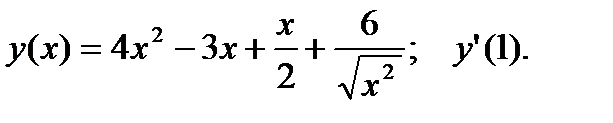 2.
2. 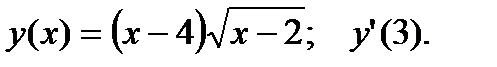
3. 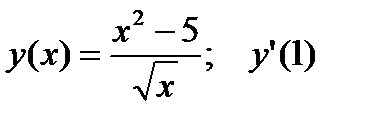 .
.
Вопросы для самоконтроля:
1. Правило дифференцирования суммы и разности двух функций.
2. Сформулируйте правило вычисления производной произведения.
3. Запишите формулу вычисления производной частного двух функций.
4. Как найти производную функции при данном значении аргумента?
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 11





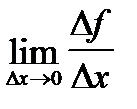 =
=  ;
;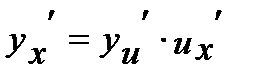 ;
;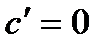 7.
7. 
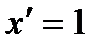 ,
, 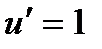 8.
8. 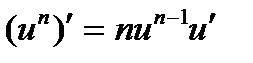
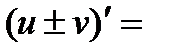
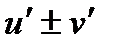 . 9.
. 9. 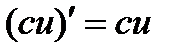 ′.
′. 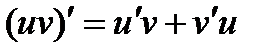 . 10.
. 10. 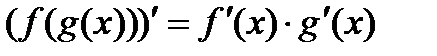
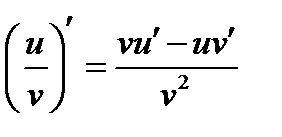 . 11.
. 11. 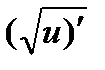 =
= 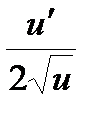 ;
; 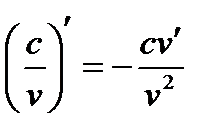 .
. 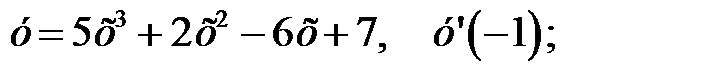
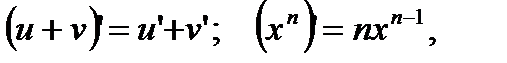 имеем:
имеем: 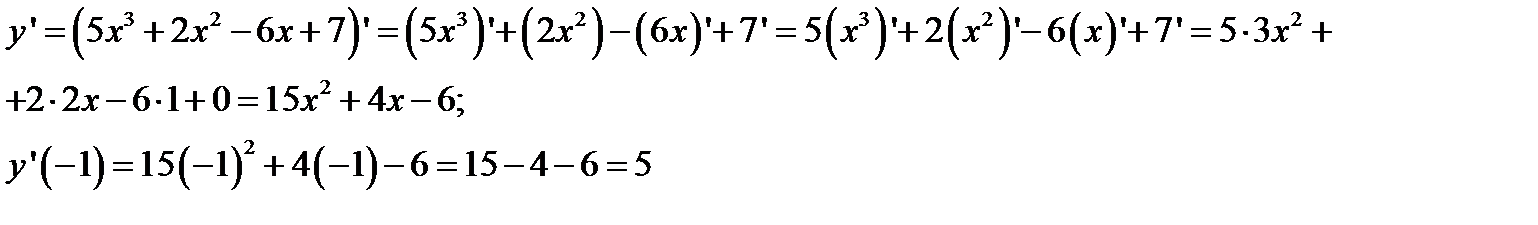
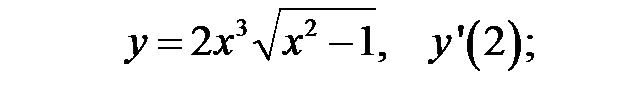
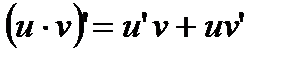 , имеем:
, имеем: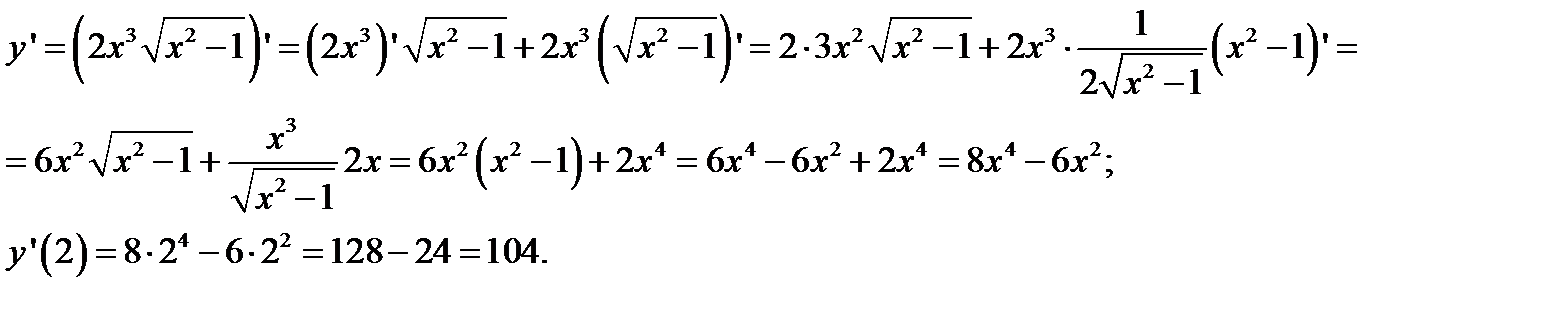
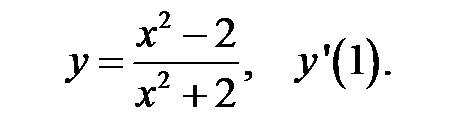
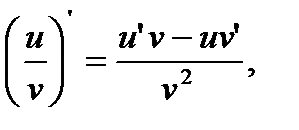 имеем:
имеем: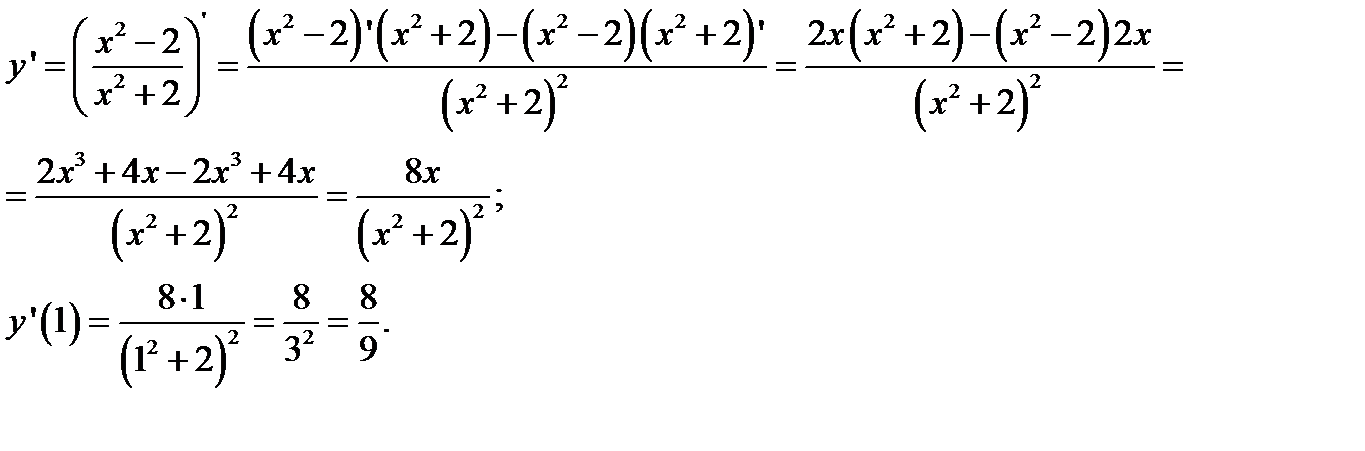
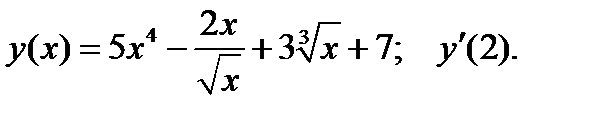 2.
2. 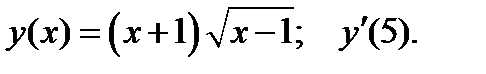
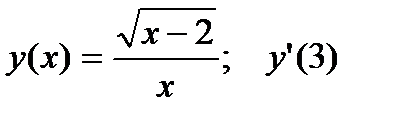 .
. 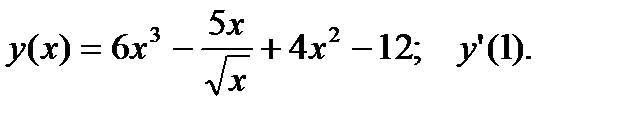 2.
2. 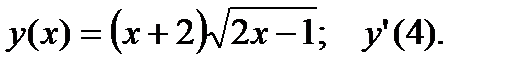
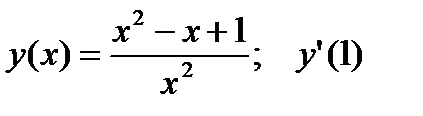 .
. 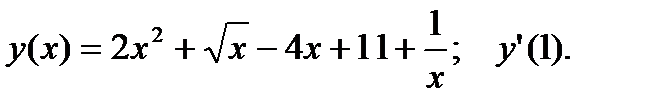 2.
2. 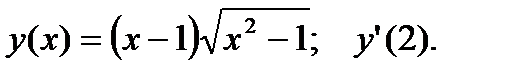
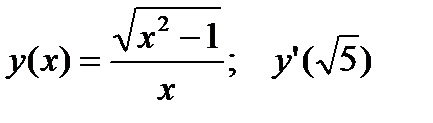 .
. 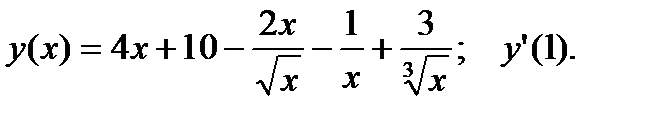 2.
2. 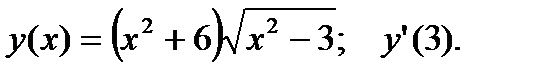
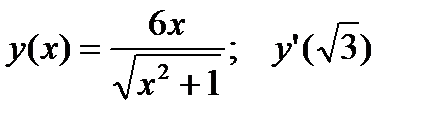 .
. 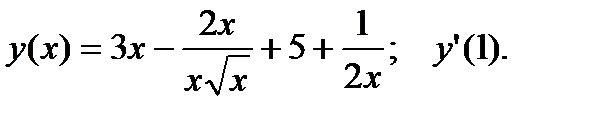 2.
2. 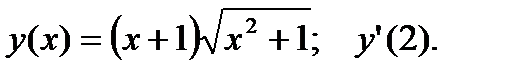
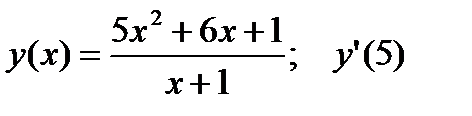
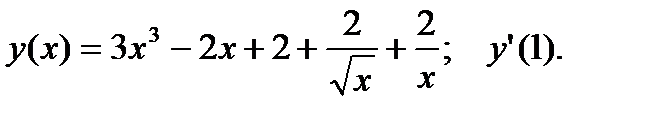 2.
2. 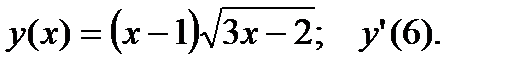
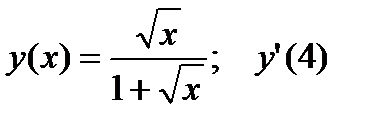 .
. 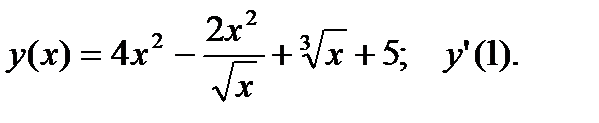 2.
2. 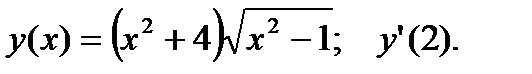
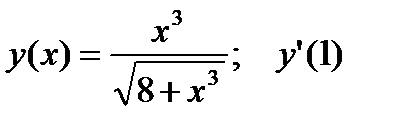 .
. 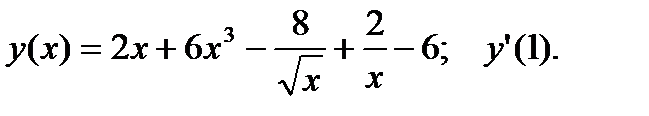 2.
2. 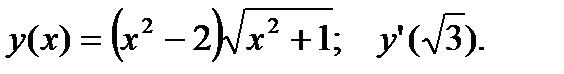
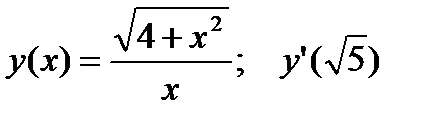 .
. 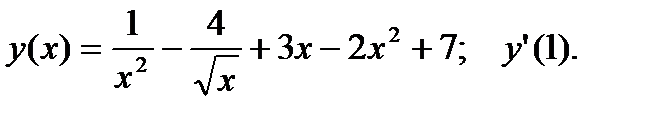 2.
2. 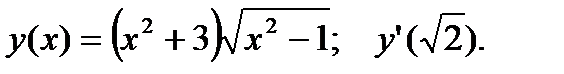
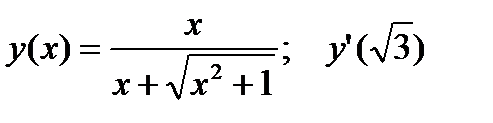 .
. 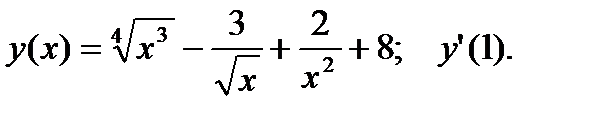 2.
2. 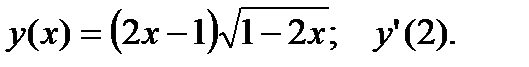
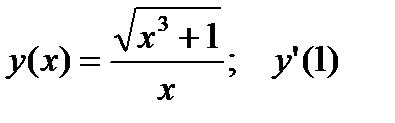 .
. 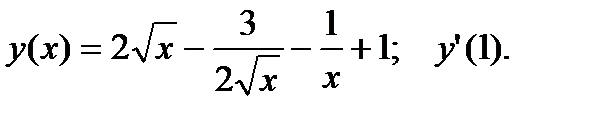 2.
2. 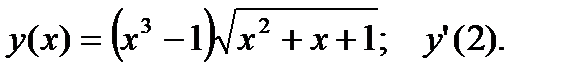
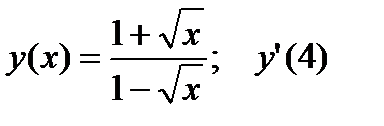 .
. 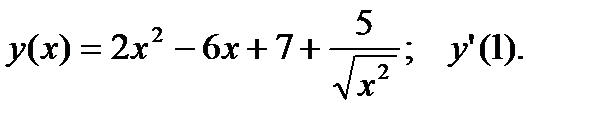 2.
2. 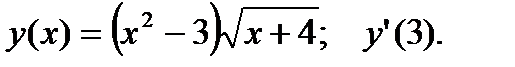
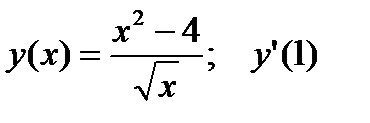 .
. 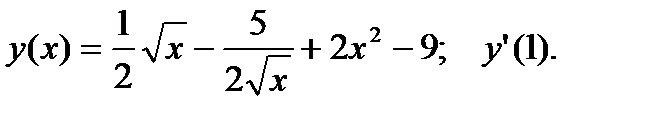 2.
2. 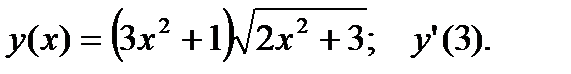
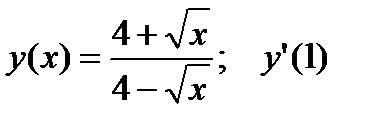 .
. 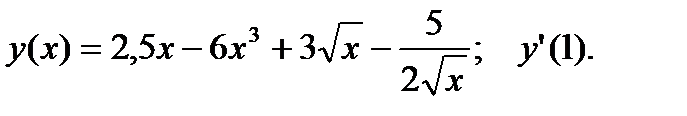 2.
2. 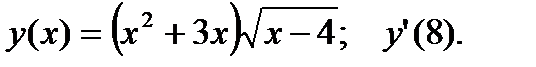
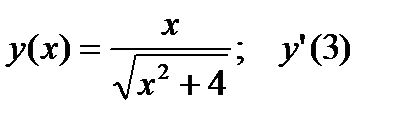 .
. 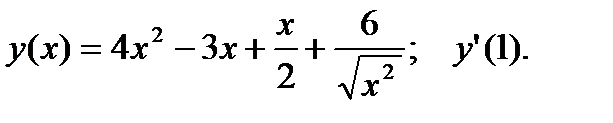 2.
2. 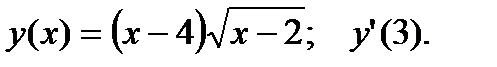
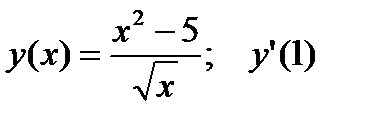 .
. 


