

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...
Топ:
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Интересное:
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Цель:
- сформировать навыки вычисления пределов в точке;
- развить умение раскрывать неопределённости вида 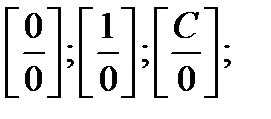
- закрепить знания о способах разложения многочлена на линейные множители;
Материально – техническое обеспечение: методические указания по выполнению работы;
Время выполнения: 2 академических часа;
Ход занятия:
1. Изучить краткие теоретические сведения;
2. Выполнить задания;
3. Сделать вывод по работе;
4. Подготовить защиту работы по контрольным вопросам.
Краткие теоретические сведения:
Предельное значение функции в заданной точке — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.
Отсутствие предела функции (в данной точке) означает, что для любого заранее заданного значения области значений и всякой его окрестности сколь угодно близко от заданной точки существуют точки, значение функции в которых окажется за пределами заданной окрестности.
Если в некоторой точке области определения функции существует предел и этот предел равен значению в данной функции, то функция оказывается непрерывной (в данной точке).
Определение 1: Пусть функция f (x) определена в некоторой окрестности точки а, кроме самой точки а. Число В называют пределом функции f(x) в точке а, если для любой последовательности значений аргументов х1, х2, х3, …, хn, стремящихся к а, последовательность соответствующих значений функции f(x1), f(x2), …, f(xn), сходится к числу В.
Обозначение: 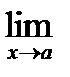 f(x) = В, если хn → а при f(xn) →В.
f(x) = В, если хn → а при f(xn) →В.
Для предела функции в точке справедливы следующие теоремы:
Теорема 1. Если 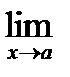 f(x) = А,
f(x) = А, 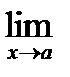 g(x) = В, то предел суммы функций f(x) и g(x) при х→а равен сумме пределов этих функций, т.е.
g(x) = В, то предел суммы функций f(x) и g(x) при х→а равен сумме пределов этих функций, т.е.
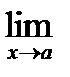 (f(x) ± g(x)) =
(f(x) ± g(x)) = 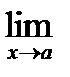 f(x) ±
f(x) ± 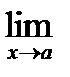 g(x).
g(x).
Теорема 2. Если f(x) и g(x) имеют пределы при х→а, то предел произведения функций при х→а равен произведению пределов этих функций, т.е.
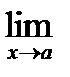 (f(x) · g(x)) =
(f(x) · g(x)) = 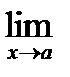 f(x) ·
f(x) · 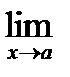 g(x).
g(x).
Следствие 1. 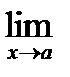 (С∙f(x)) = С ∙
(С∙f(x)) = С ∙ 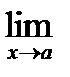 f(x).
f(x).
Следствие 2. 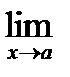 С = С.
С = С.
Теорема 3. Если функции f(x) и g(x) имеют пределы при х→а, причем предел функции g(x) ≠ 0, то имеет место равенство:
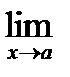
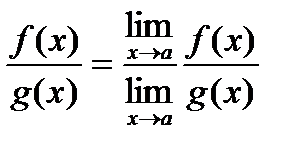 .
.
Рассмотрим вычисление пределов функций на конкретных примерах.
Пример 1. Найти предел в заданной точке:
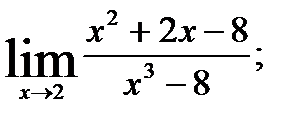
Решение:
При непосредственной подстановке х = 2 получим неопределенность вида [0/0]. Раскрыть эту неопределенность возможно, разложив числитель и знаменатель на линейные множители по формулам:
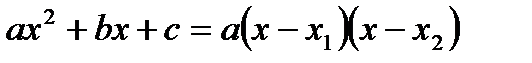 , , 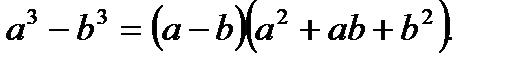
|
Далее сократим дробь на х – 2 и найдём значение предела при х = 2:
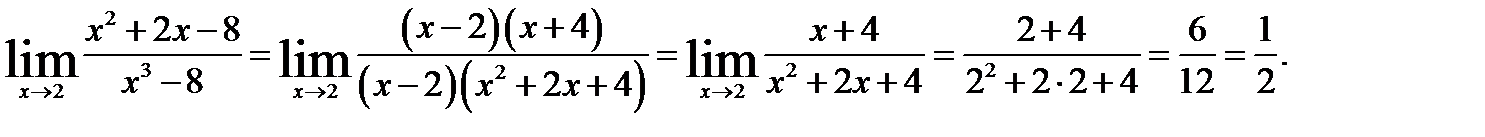
Пример 2. Найти предел в заданной точке:
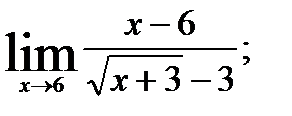
Решение:
В данном случае пределы числителя и знаменателя при 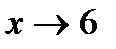 равны нулю, имеем неопределенность вида [0/0].
равны нулю, имеем неопределенность вида [0/0].
Умножаем числитель и знаменатель на сопряженный знаменателю множитель 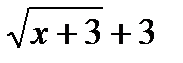 и, затем сократив дробь на х – 6 , получим:
и, затем сократив дробь на х – 6 , получим:
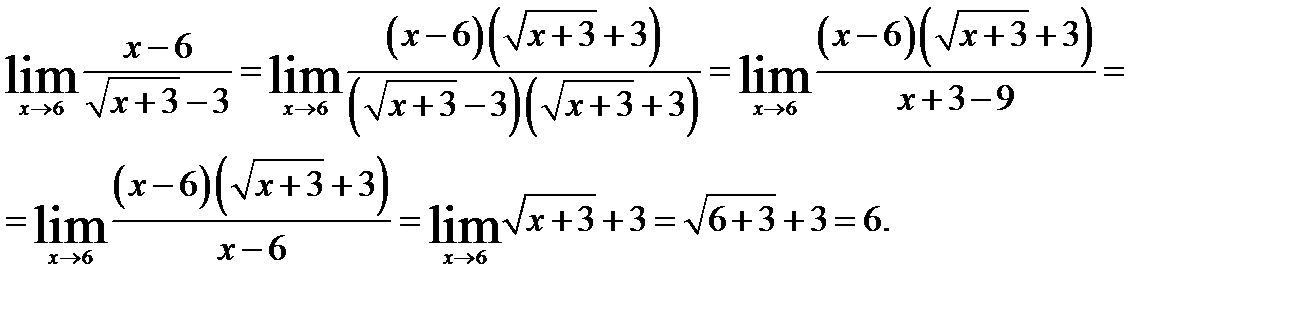
Задания для самостоятельного выполнения:
Найти пределы функций в заданных точках.
Вариант 1.
1. 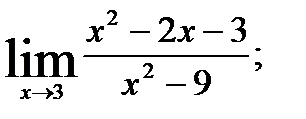 2.
2. 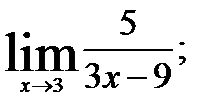 3.
3. 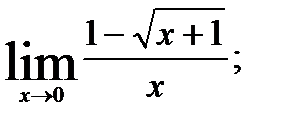
Вариант 2.
1.  2.
2. 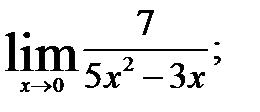 3.
3. 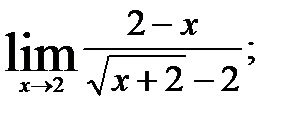
Вариант 3.
1. 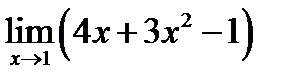 ; 2.
; 2. 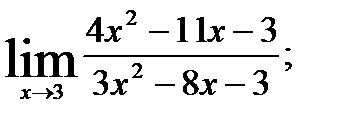 3.
3. 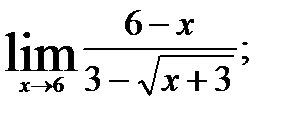
Вариант 4.
1. 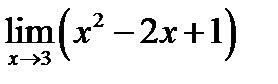 ; 2.
; 2. 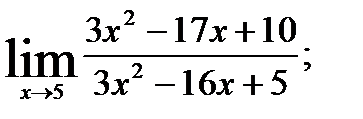 3.
3. 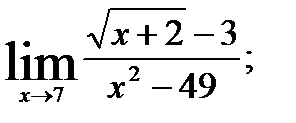
Вариант 5.
1. 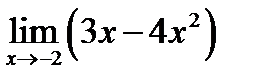 ; 2.
; 2. 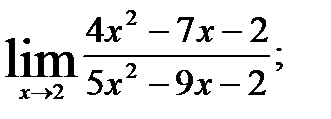 3.
3. 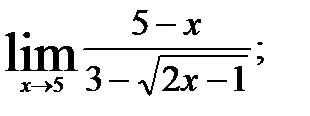
Вариант 6.
1. 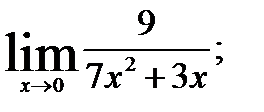 2.
2. 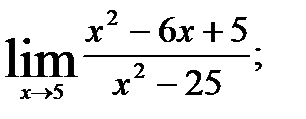 3.
3. 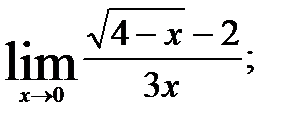
Вариант 7.
1. 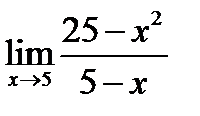 ; 2.
; 2. 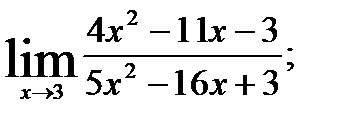 3.
3. 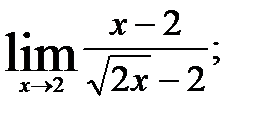
Вариант 8.
1. 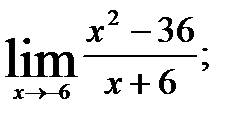 2.
2. 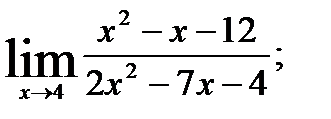 3.
3. 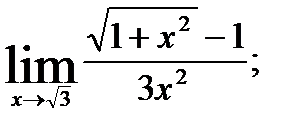
Вариант 9.
1. 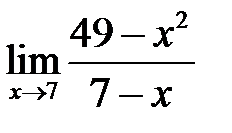 ; 2.
; 2. 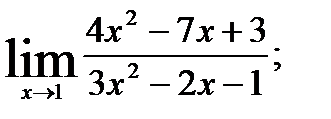 3.
3. 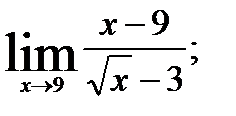
Вариант 10.
1. 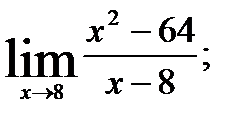 2.
2. 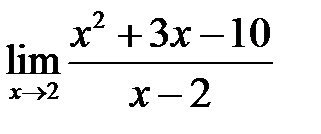 ; 3.
; 3. 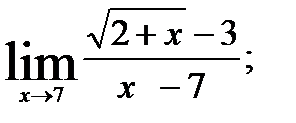
Вариант 11.
1. 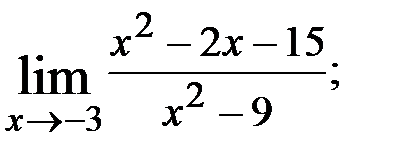 2.
2. 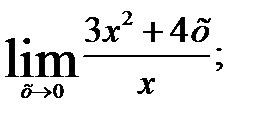 3.
3. 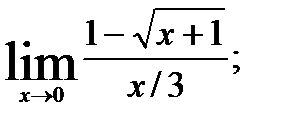
Вариант 12.
1. 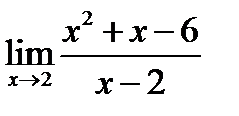 ; 2.
; 2. 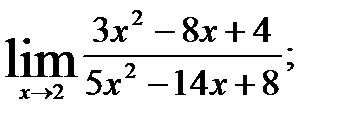 3.
3. 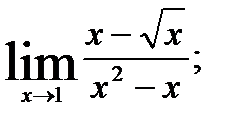
Вариант 13.
1. 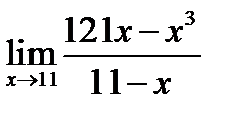 ; 2.
; 2. 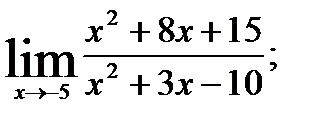 3.
3. 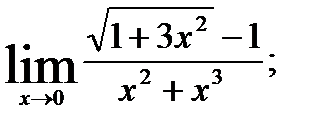
Вариант 14.
1. 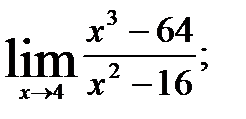 2.
2. 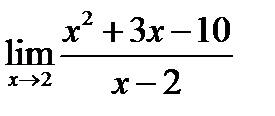 ; 3.
; 3. 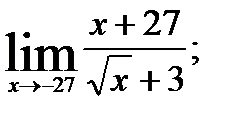
Вариант 15.
1. 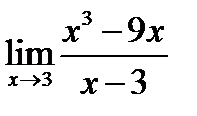 ; 2.
; 2. 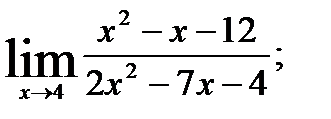 3.
3. 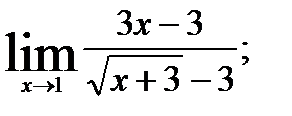
Вопросы для самоконтроля:
1. Назовите основные методы вычисления пределов в точке.
2. Сформулируйте теоремы о пределах.
3. Запишите формулу разложения квадратного трёхчлена.
4. Запишите формулы разности квадратов и разности кубов.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 8
|
|
|

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...
© cyberpedia.su 2017-2025 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!