Приложения неопределённого интеграла

К РЕШЕНИЮ ЗАДАЧ

Цель:

- сформировать навыки нахождения функции по её дифференциалу;

        - развить умение  составлять уравнение кривой, проходящей через данную точку с заданным угловым коэффициентом;

        - закрепить знания о физических приложениях неопределённого интеграла;

   Материально – техническое обеспечение: методические указания по выполнению работы, стенды «Таблица интегралов»;

Время выполнения: 2 академических часа;

Ход занятия:

1. Изучить краткие теоретические сведения;

2. Выполнить задания;

3. Сделать вывод по работе;

4. Подготовить защиту работы по контрольным вопросам.

Краткие теоретические сведения:

 Отыскание функции по заданной производной или по дифференциалу - задача неопределённая, так как 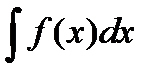 есть множество первообразных функций вида  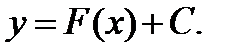Чтобы из множества первообразных выделить одну определённую функцию, должны быть заданы начальные условия - частные значения х и у, по которым находят единственное значение С, удовлетворяющее этим начальным условиям.

Пример 1. Найти функцию по её дифференциалу  если у = 2 при х = 3.

Решение:

Проинтегрируем обе части данного равенства: 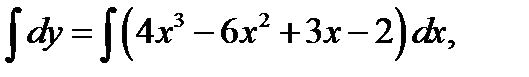 откуда  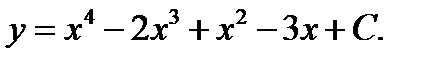Найдём значение постоянной С при заданных начальных условиях у = 2 при х = 3:  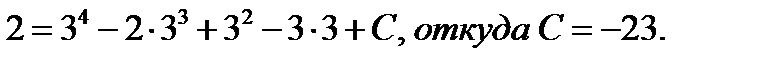Итак, функция, удовлетворяющая заданным начальным условиям, имеет вид: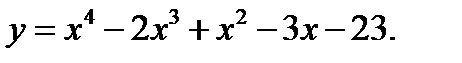

Пример 2. Составить уравнение кривой, проходящей через точку 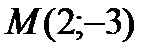и имеющей касательную с угловым коэффициентом k =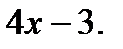

Решение:

Согласно условию: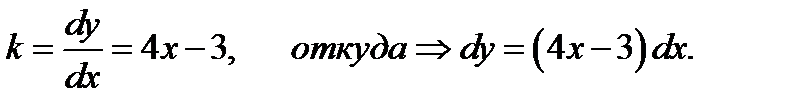

Проинтегрировав обе части равенства, получим:

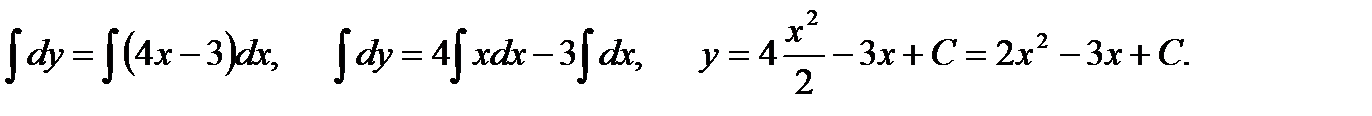
Используя  начальные условия 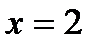 и 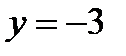, находим С:

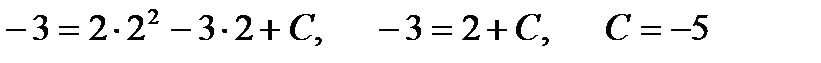
Следовательно, искомое уравнение кривой имеет вид:

Пример 3. Скорость прямолинейного движения точки задана уравнением 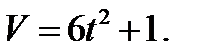 Найти закон движения, если за время  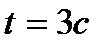точка прошла путь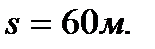

Решение:

Имеем: 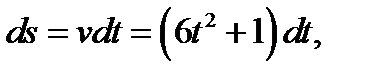 тогда:

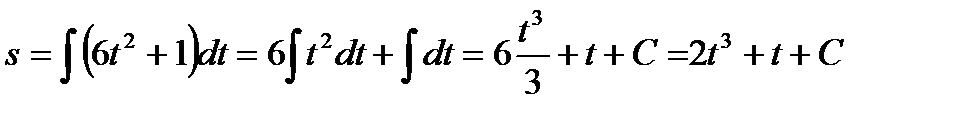
Подставив в найденное уравнение начальные условия: 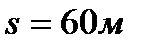, , 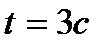получим 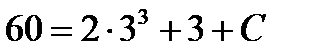, откуда  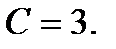Закон движения примет вид: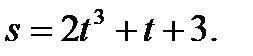

Задания для самостоятельного выполнения:

I.  Найти функцию по её дифференциалу.

II. Составить уравнение кривой, проходящей через точку М (х; у) с заданным угловым коэффициентом .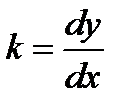

III. Найти закон прямолинейного движения точки.

Вариант 1.

1. 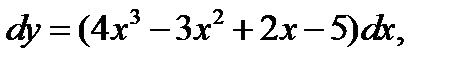если у = 2 при х = 2.

2. М ( 1; 2 )  и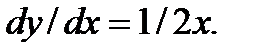

3. 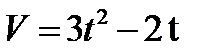, если t = 3с  при S = 10м.

Вариант 2.

1. 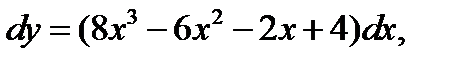 если у = 6 при х = 1.

2. М ( 2; 1 )  и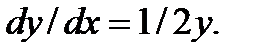

3. 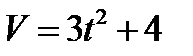, если t = 2с  при S = 20м.

Вариант 3.

1. 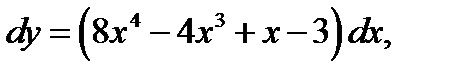 если у = 3 при х = 2.

2. М ( 2; 2)  и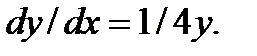

3. 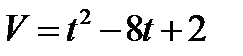, если t = 3с  при S = 30м.

Вариант 4.

1. 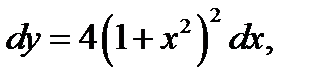 если у = 4 при х = 3.

2. М ( 1 ; 3 )  и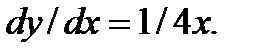

3. 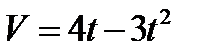, если t = 2с  при S = 40м.

Вариант 5.

1. 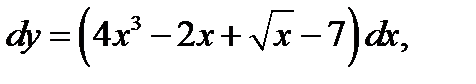 если у = 2 при х = 1.

2. М ( 5 ; -2 )  и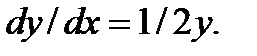

3. 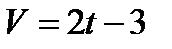, если t = 0с  при S = 6м.

Вариант 6.

1. 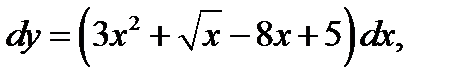 если у = 5 при х = 1.

2. М ( 4 ; 3 )  и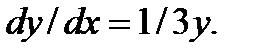

3. 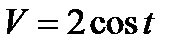, если t = 𝜋 ∕6 с  при S = 4м.

Вариант 7.

1. 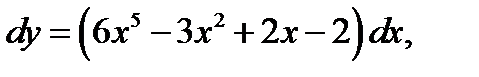 если у = 3 при х = 2.

2. М ( 3 ; 1 )  и k =2 x-1.

3. 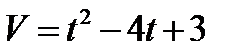, если t = 3с  при S = 20м.

Вариант 8.

1. 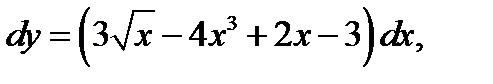 если у = 4 при х = 1.

2. М ( 0 ; 3 )  и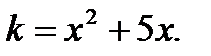

3. 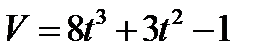, если t = 1с  при S = 5м.

Вариант 9.

1. 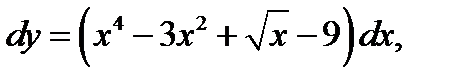 если у = 2 при х = 1.

2.  М ( 2 ; -1 )  и  k =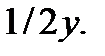

3. 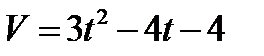, если t = 2с  при S = 8м.

Вариант 10.

1. 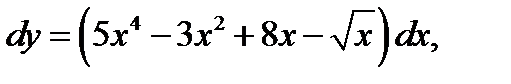 если у = 5 при х = 1.

2.  М ( 1 ; 3 )  и  k = 2 x-3. 

3. 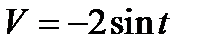, если t = 𝜋 ∕3 с  при S = 5м.

Вариант 11.

1. 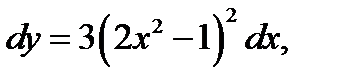 если у = 6 при х = 4.

2.  М ( 1 ; 3 )  и  k = -2 x. 

3. 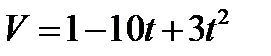, если t = 0с  при S = 10м.

Вариант 12.

1. 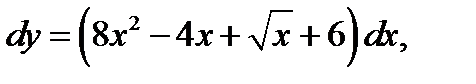 если у = 3 при х = 1.

2.  М ( 1 ; e )  и .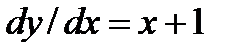

3. 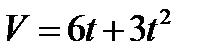, если t = 2с  при S = 40м.

Вариант 13.

1. 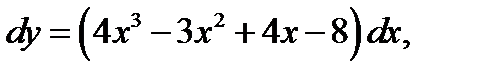 если у = 5 при х = 3.

2. М ( -2 ; -8/3 )  и .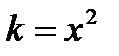

3. 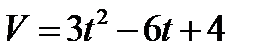, если t = 0с  при S = 8м.

Вариант 14.

 1. 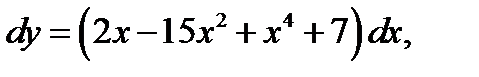 если у = 3 при х = 2.

 2.  М ( 0 ; 4 )  и  k = 3 x-4.

 3. 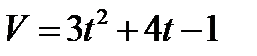, если t = 0с  при S = 0м.

Вариант 15.

1.  если у = 4 при х = 1.

2.  М ( 1 ; 3 )  и  k = 3 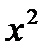+2.

3. 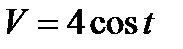, если t = 𝜋 ∕6 с  при S = 8м.

Вопросы для самоконтроля:

1. Как найти функцию по её дифференциалу?

2. Опишите алгоритм нахождения уравнения кривой, проходящей через данную точку с заданным угловым коэффициентом.

3. Сформулируйте физические приложения неопределённого интеграла.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 16