

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...
Топ:
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Интересное:
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
В АЛГЕБРАИЧЕСКОЙ ФОРМЕ
Цель:
- сформировать умения выполнения действий над комплексными числами в алгебраической форме;
- развить навыки преобразования мнимой единицы;
- закрепить знания о свойствах степени;
Материально – техническое обеспечение: методические указания по выполнению работы, плакат свойства степени;
Время выполнения: 2 академических часа;
Ход занятия:
1. Изучить краткие теоретические сведения;
2. Выполнить задания;
3. Сделать вывод по работе;
4. Подготовить защиту работы по контрольным вопросам.
Краткие теоретические сведения:
Сложение, вычитание, умножение и деление комплексных чисел в алгебраической форме производится по правилам соответствующих действий над многочленами.
Пример 1. Выполнить сложение, вычитание, умножение и деление комплексных чисел:
Решение:
1. Сложение комплексных чисел: 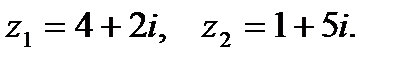
По правилу сложения комплексных чисел получим:
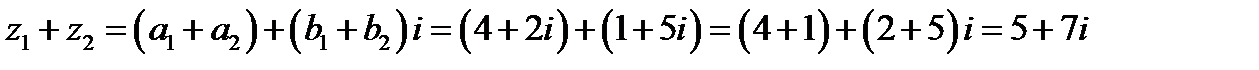 .
.
2. Вычитание комплексных чисел: 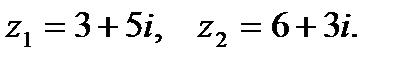
По правилу вычитания комплексных чисел получим:
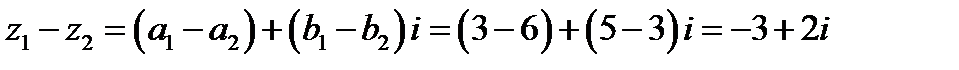 .
.
3. Умножение комплексных чисел: 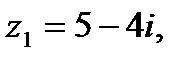
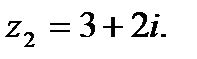
По правилу умножения комплексных чисел получим:
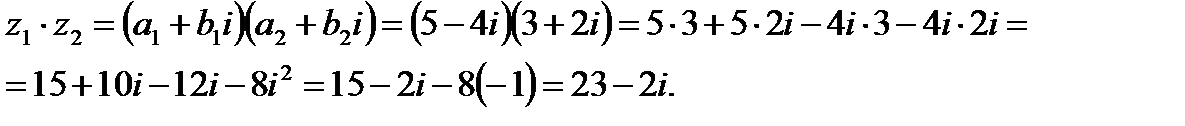
4. Деление комплексных чисел: 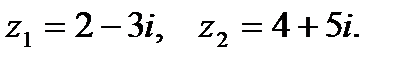
Умножаем делимое и делитель на множитель, сопряженный делителю:
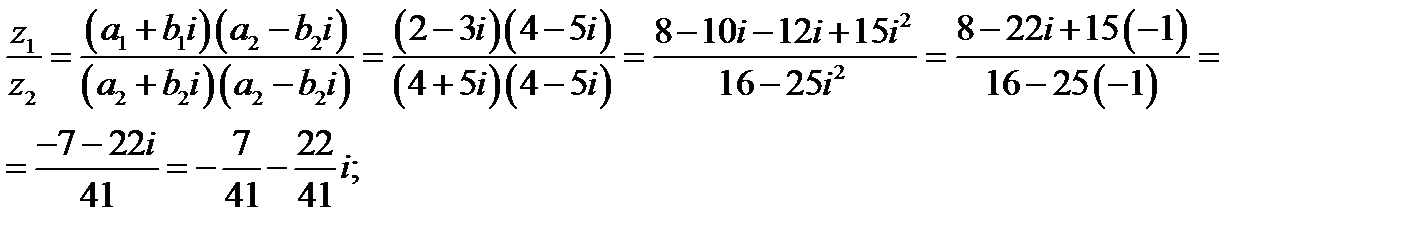
Пример 2. Вычислить: 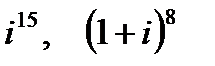
Решение:
1. Так как 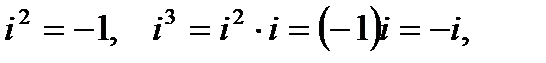 получим:
получим:
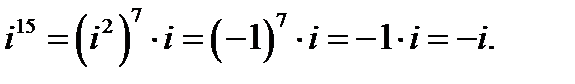
2. Используя соотношение 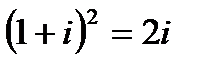 , получим:
, получим:
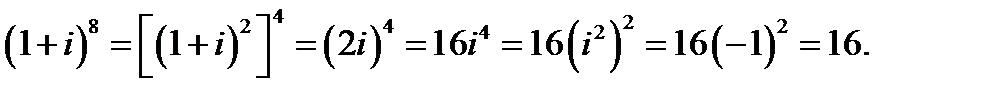
Задания для самостоятельного выполнения:
I. Выполните сложение, вычитание, умножение и деление комплексных чисел в алгебраической форме.
II. Возведите в степень.
Вариант 1.
1. а) 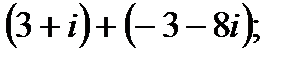 в)
в) 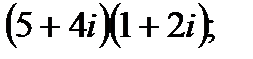
б) 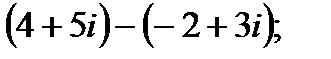 г)
г) 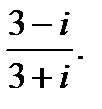
2. а) 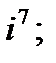 б)
б) 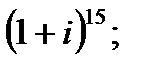 в)
в) 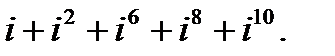
Вариант 2.
1. а) 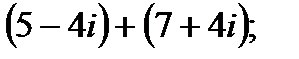 в)
в) 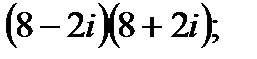
б) 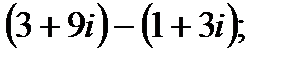 г)
г) 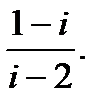
2. а) 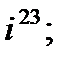 б)
б) 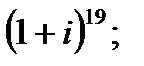 в)
в) 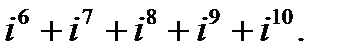
Вариант 3.
1. а) 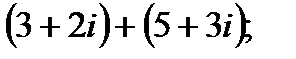 в)
в) 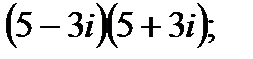
б) 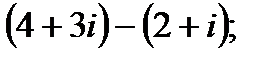 г)
г) 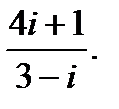
2. а) 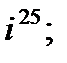 б)
б) 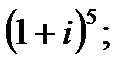 в)
в) 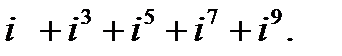
Вариант 4.
1. а) 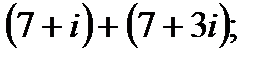 в)
в) 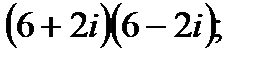
б) 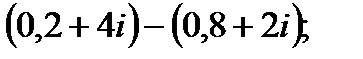 г)
г) 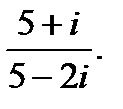
2. а) 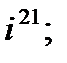 б)
б) 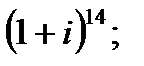 в)
в) 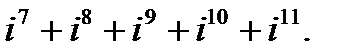
Вариант 5.
1. а) 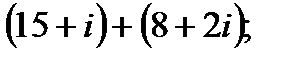 в)
в) 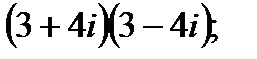
б) 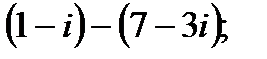 г)
г) 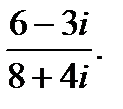
2. а) 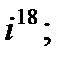 б)
б) 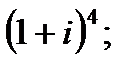 в)
в) 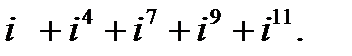
Вариант 6.
1. а) 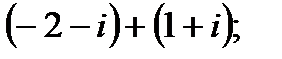 в)
в) 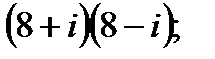
б) 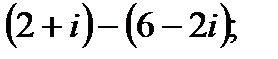 г)
г) 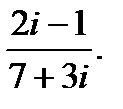
2. а) 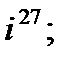 б)
б) 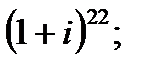 в)
в) 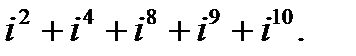
Вариант 7.
1. а) 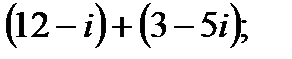 в)
в) 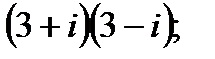
б) 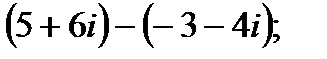 г)
г) 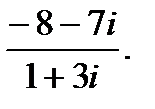
2. а) 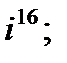 б)
б) 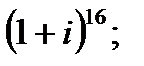 в)
в) 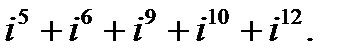
Вариант 8.
1. а) 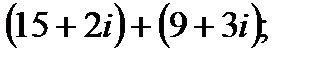 в)
в) 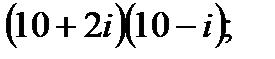
б) 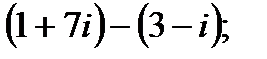 г)
г) 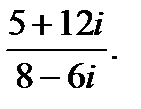
2. а) 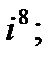 б)
б) 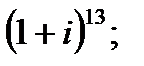 в)
в) 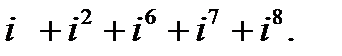
Вариант 9.
1. а) 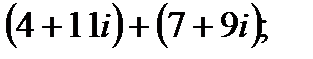 в)
в) 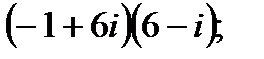
б) 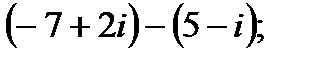 г)
г) 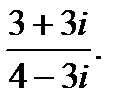
2. а) 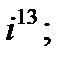 б)
б) 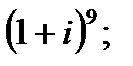 в)
в) 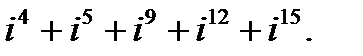
Вариант 10.
1. а) 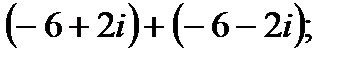 в)
в) 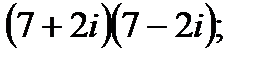
б) 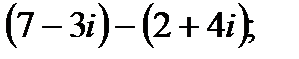 г)
г) 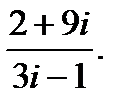
2. а) 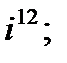 б)
б) 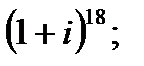 в)
в) 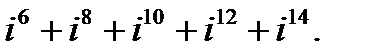
Вариант 11.
1. а) 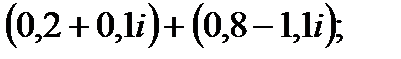 в)
в) 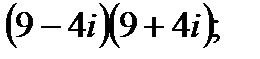
б) 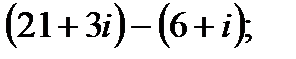 г)
г) 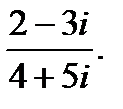
2. а) 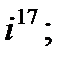 б)
б) 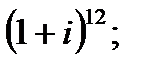 в)
в) 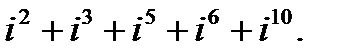
Вариант 12.
1. а) 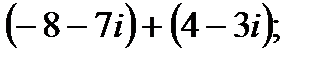 в)
в) 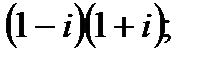
б) 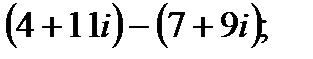 г)
г) 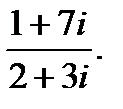
2. а) 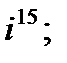 б)
б) 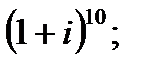 в)
в) 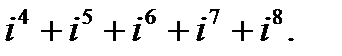
Вариант 13.
1. а) 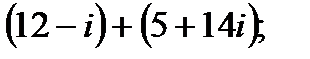 в)
в) 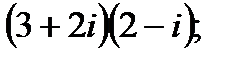
б) 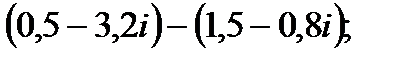 г)
г) 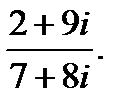
2. а) 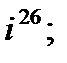 б)
б)  в)
в) 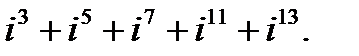
Вариант 14.
1. а) 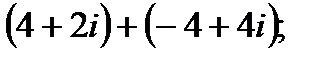 в)
в) 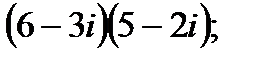
б) 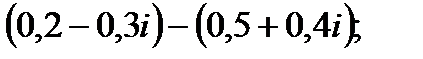 г)
г) 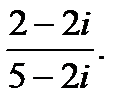
2. а) 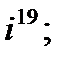 б)
б) 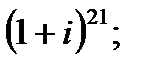 в)
в) 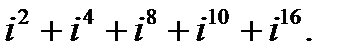
Вариант 15.
1. а) 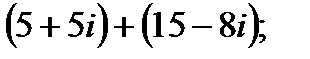 в)
в) 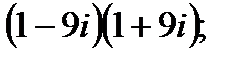
б) 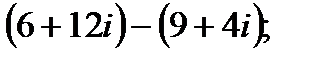 г)
г) 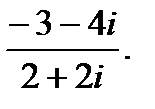
2. а) 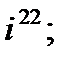 б)
б) 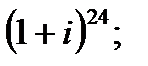 в)
в) 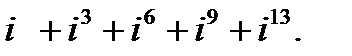
Вопросы для самоконтроля:
1. Дайте определение равным, противоположным, сопряженным, мнимым комплексным числам.
2. Запишите алгебраическую форму комплексного числа.
3. Как выполняются действия над комплексными числами в алгебраической форме?
4. Правило вычисления натуральных степеней мнимой единицы?
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2
ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ
В ТРИГОНОМЕТРИЧЕСКОЙ ФОРМЕ
Цель:
- сформировать навыки вычисления модуля и аргумента комплексного числа;
- развить умения выполнения действий над комплексными числами в тригонометрической форме;
- закрепить навыки преобразований комплексных чисел из алгебраической формы в тригонометрическую и наоборот;
Материально – техническое обеспечение: методические указания по выполнению работы, таблица значений тригонометрических функций;
Время выполнения: 2 академических часа;
Ход занятия:
1. Изучить краткие теоретические сведения;
2. Выполнить задания;
3. Сделать вывод по работе;
4. Подготовить защиту работы по контрольным вопросам.
Краткие теоретические сведения:
Для выполнения действий умножения, деления, возведения в степень, извлечения корня n-ой степени над комплексными числами в тригонометрической форме необходимо знание соответствующих формул.
Пример 1. Выполнить умножение комплексных чисел 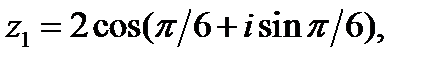
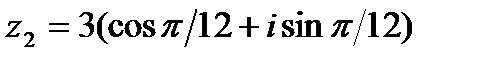 в тригонометрической форме.
в тригонометрической форме.
Решение:
Найдем произведение двух комплексных чисел по заданной формуле:
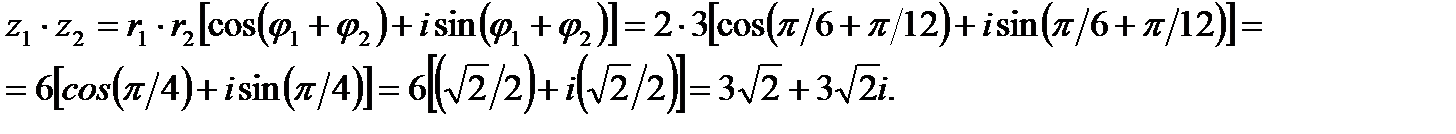
Пример 2. Выполнить деление комплексных чисел 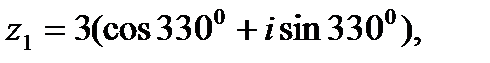
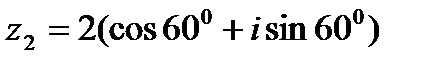 в тригонометрической форме.
в тригонометрической форме.
Решение:
Выполним деление двух комплексных чисел по заданной формуле:
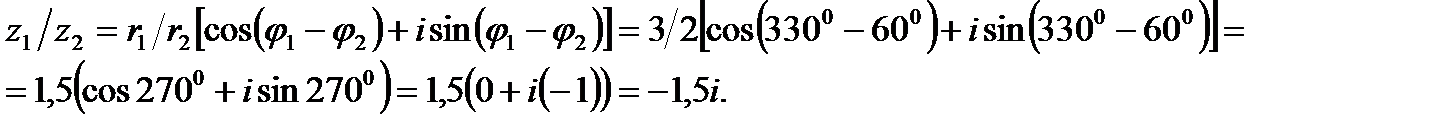
Пример 3. Возвести в степень: 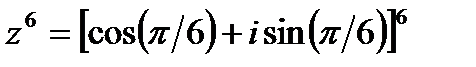 .
.
Решение:
По формуле Муавра получим:
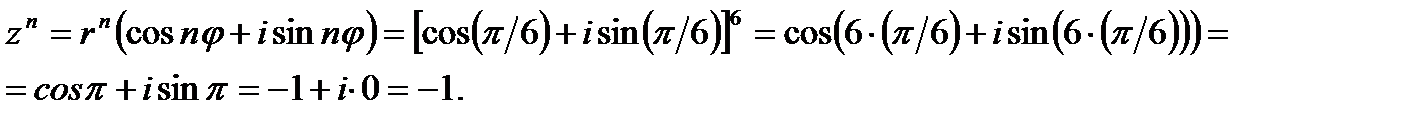
Пример 4. Найти значение корня из комплексного числа 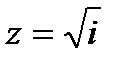 .
.
Решение:
Во-первых, представим число i в тригонометрической форме: 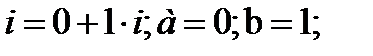 Находим модуль по формуле
Находим модуль по формуле 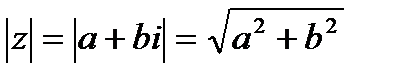 .
.
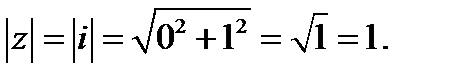
Точка, изображающая число z, лежит в I четверти, тогда, 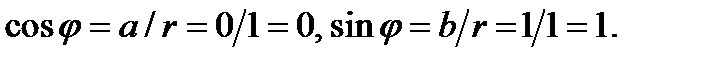 Определим по таблице значений тригонометрических функций главное значение аргумента:
Определим по таблице значений тригонометрических функций главное значение аргумента: 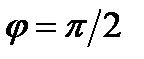 . Поэтому, тригонометрическая форма числа
. Поэтому, тригонометрическая форма числа 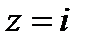 примет вид:
примет вид:
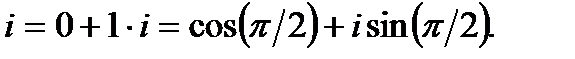
Теперь найдём значение корня по формуле:
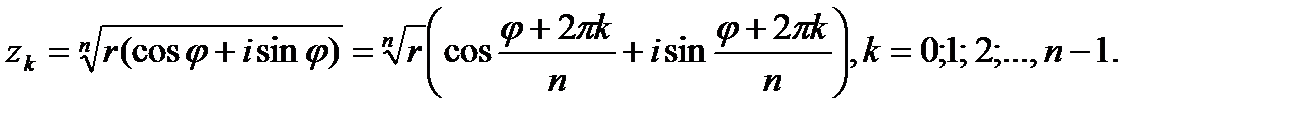
Находим:
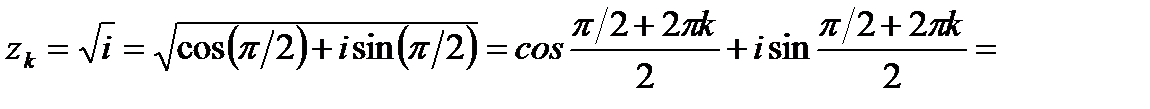
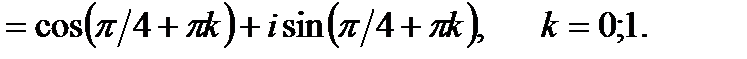
если 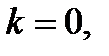 то
то 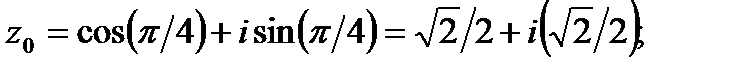
если 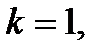 то
то 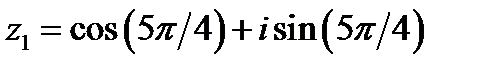
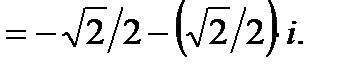
Пример 5. Преобразуйте алгебраическую форму комплексного числа 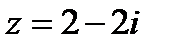 в тригонометрическую.
в тригонометрическую.
Решение:
Для перевода комплексного числа 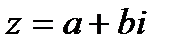 из алгебраической формы в тригонометрическую необходимо найти его модуль и главное значение аргумента. Здесь
из алгебраической формы в тригонометрическую необходимо найти его модуль и главное значение аргумента. Здесь 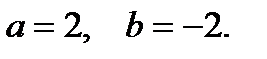 Находим модуль по формуле
Находим модуль по формуле 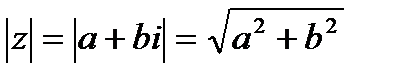 .
.
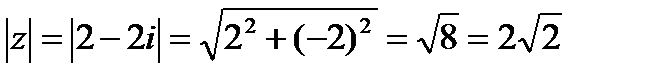 .
.
Точка, изображающая число z, лежит в IV четверти, тогда 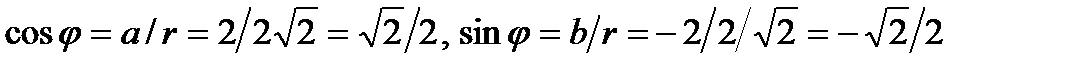 .Определим по таблице значений тригонометрических функций главное значение аргумента:
.Определим по таблице значений тригонометрических функций главное значение аргумента: 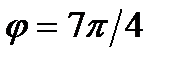 . Поэтому, тригонометрическая форма числа
. Поэтому, тригонометрическая форма числа 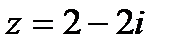 примет вид:
примет вид:
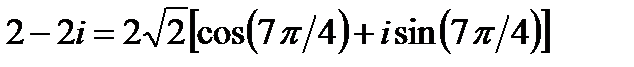 .
.
Задания для самостоятельного выполнения:
I. Выполните умножение комплексных чисел в тригонометрической форме.
II. Выполните деление комплексных чисел в тригонометрической форме.
III. Возведите в степень.
IV.Представьте число в тригонометрической форме и найдите значение корня.
V.Преобразуйте алгебраическую форму комплексного числа в тригонометрическую.
Вариант 1.
1. 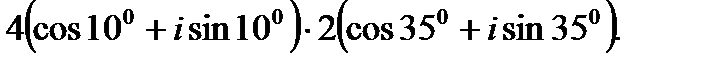
2. 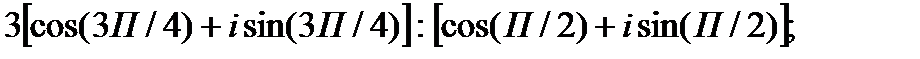
3. 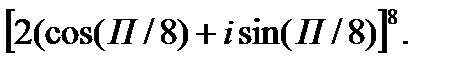
4. 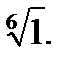
5. 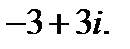
Вариант 2.
1. 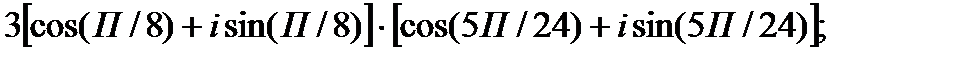
2. 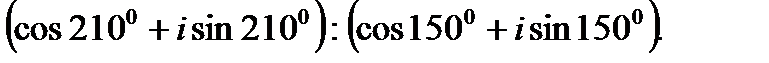
3. 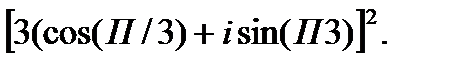
4. 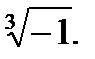
5. 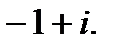
Вариант 3.
1. 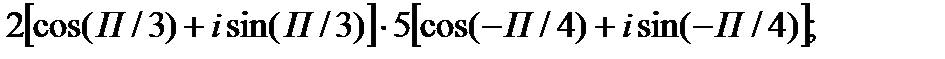
2. 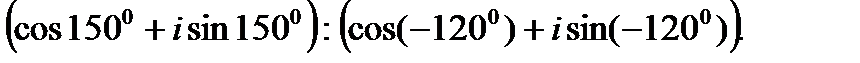
3. 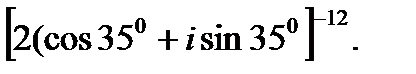
4. 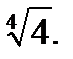
5. 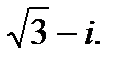
Вариант 4.
1. 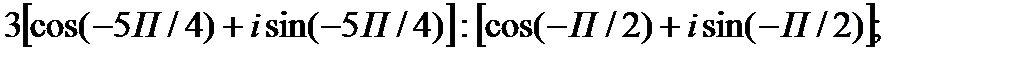
2. 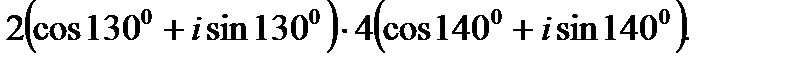
3. 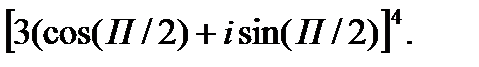
4. 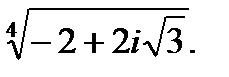
5. 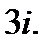
Вариант 5.
1. 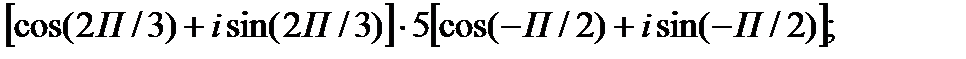
2. 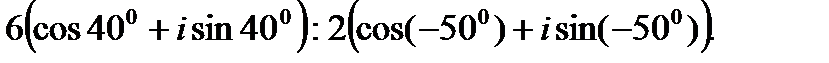
3. 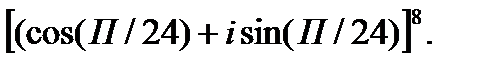
4. 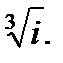
5. 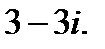
Вариант 6.
1. 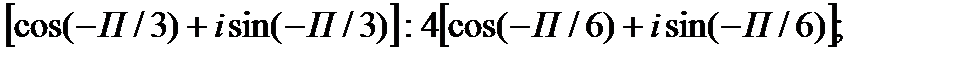
2. 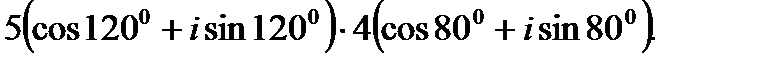
3. 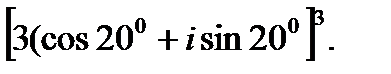
4. 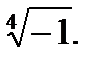
5. 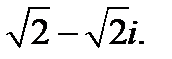
Вариант 7.
1. 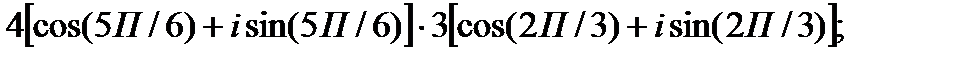
2. 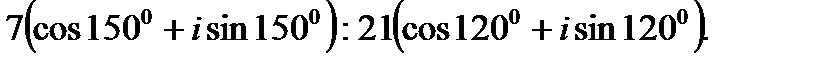
3. 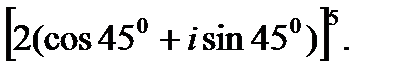
4. 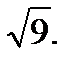
5. 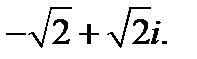
Вариант 8.
1. 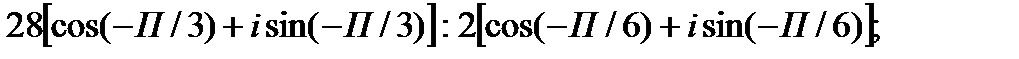
2. 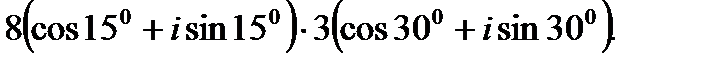
3. 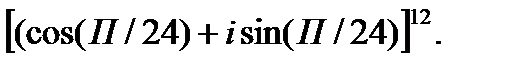
4. 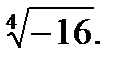
5. 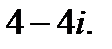
Вариант 9.
1. 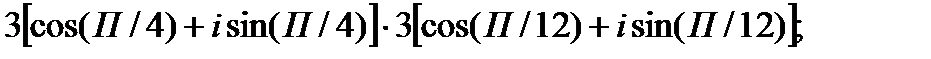
2. 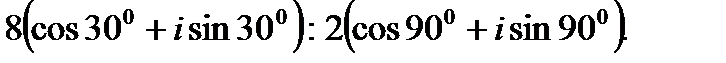
3. 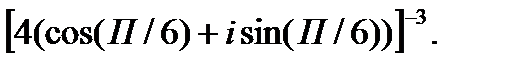
4. 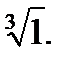
5. 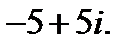
Вариант 10.
1. 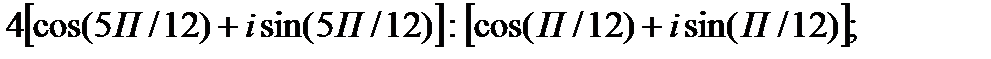
2. 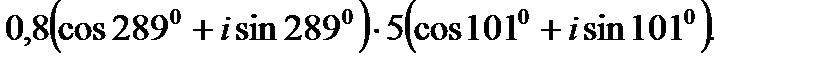
3. 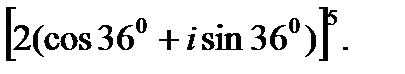
4. 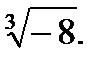
5. 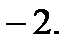
Вариант 11.
1. 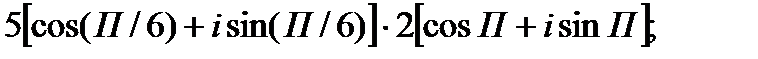
2. 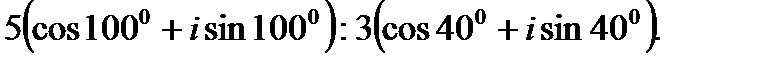
3. 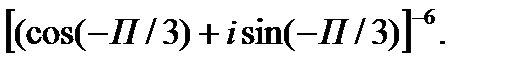
4. 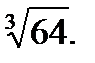
5. 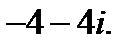
Вариант 12.
1. 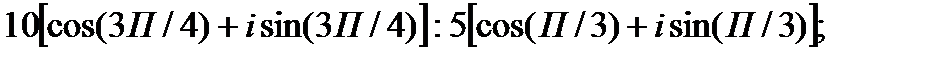
2. 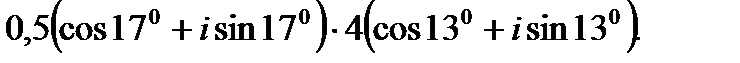
3. 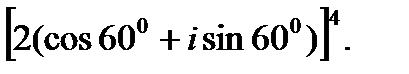
4. 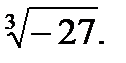
5. 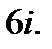
Вариант 13.
1. 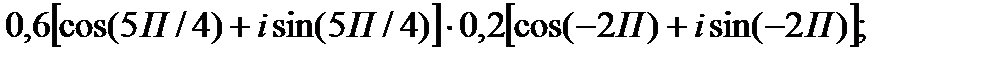
2. 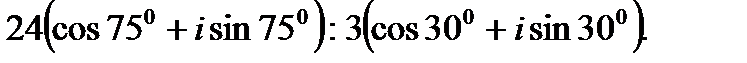
3. 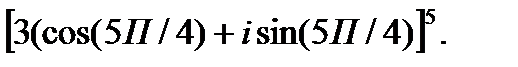
4. 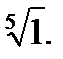
5. 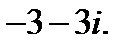
Вариант 14.
1. 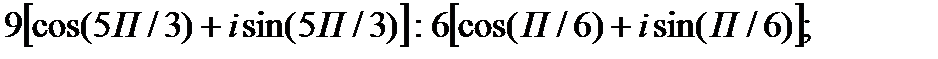
2. 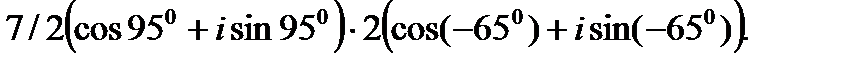
3. 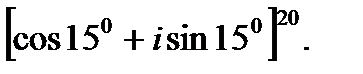
4. 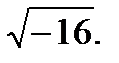
5. 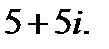
Вариант 15.
1. 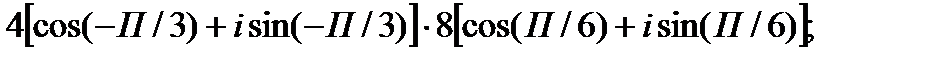
2. 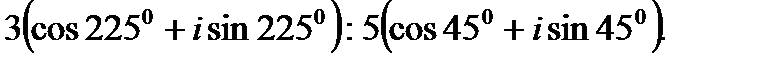
3. 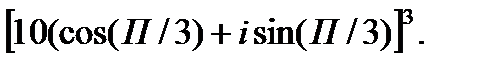
4. 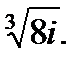
5. 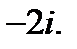
Вопросы для самоконтроля:
1. Что называют модулем и аргументом комплексного числа?
2. Как представить комплексное число в тригонометрической форме?
3. Правила умножения и деления комплексных чисел в тригонометрической форме.
4. Запишите формулу Муавра.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 3
|
|
|

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...
© cyberpedia.su 2017-2025 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!