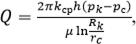Интерпретация уравнения Бернулли для установившегося потока реальной жидкости с геометрической точки зрения.

Геометрическая интерпретация уравнения Бернулли

Положение любой частицы жидкости относительно некоторой произвольной линии нулевого

уровня 0-0 определяется вертикальной координатой Z. Для реальных гидравлических систем это может быть уровень, ниже которого жидкость из данной гидросистемы вытечь не может.

Например, уровень пола цеха для станка или уровень подвала дома для домашнего водопровода.

Как и в гидростатике, величину Z называют нивелирной высотой.

 

Второе слагаемое - носит название пьезометрическая высота. Эта величина соответствует высоте, на которую поднимется жидкость в пьезометре, если его установить в рассматриваемом сечении, под действием давления P.

 

Сумма первых двух членов уравнения      ¾ гидростатический напор.

 

Третье слагаемое в уравнения Бернулли называется скоростной высотой или скоростным напором. Данную величину можно представить как высоту, на которую поднимется жидкость,

начавшая двигаться вертикально со скорость u при отсутствии сопротивления движению.

Сумму всех трёх членов (высот) называют гидродинамическим или полным напором и, как уже было сказано, обозначают буквой Н.

Все слагаемые уравнения Бернулли имеют размерность длины и их можно изобразить графически.

 

Значения              - нивелирную, пьезометрическую и скоростную высоты можно определить для каждого сечения элементарной струйки жидкости. Геометрическое место точек,

 

высоты которых равны     , называется

пьезометрической линией. Если к этим высотам

 

добавить скоростные высоты, равные, то получится другая линия, которая называется гидродинамической или напорной линией.

Из уравнения Бернулли для струйки невязкой жидкости (и графика) следует, что гидродинамический напор по длине струйки постоянен.

2 Неоднородность пластов: схемы, начальные и граничные условия.

Часто встречаются пласты, значительные области которых сильно отличаются друг от друга по фильтрационным характеристикам. Можно выделить два основных вида

неоднородностей такого типа: слоисто- неоднородные пласты; зонально-неоднородные пласты. Слоисто-неоднородный пласт состоит из пропластков разной толщины hi и

проницаемости ki

В случае непроницаемых границ между пропластками каждый пропласток можно считать как отдельный пласт, со своей проницаемостью, толщиной и дебитом Qi. Поэтому дебит скважины в слоисто-неоднородном продуктивном пласте определяется по формуле

Зонально-неоднородный пласт состоит из n-кольцевых зон (рис. 2.8). В пределах каждой i-й зоны (i = 1,2...n) проницаемость постоянна и равна ki. Наружный и внутренний радиусы зоны равны соответственно Ri, Ri-1. Причем внутренний радиус первой зоны равен

радиусу скважины Ro=rc, давление жидкости на этой границе равно давлению на

скважине po = pc. Наружный радиус последней зоны равен радиусу контура питания Rn = Rk, а давление на нем рn = pk.

  

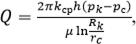
Чтобы получить решение системы уравнений, необходима конкретизация начальных и граничных условий. Продуктивный пласт или выделенную из него часть можно рассматривать как некоторую область пространства, ограниченную поверхностями – границами. Границы могут быть

непроницаемыми для жидкостей или газов(флюидов), кровля и подошва пласта. Граничной поверхностью является также поверхность, из которой пласт сообщается с областью питания, это так называемый контур питания; стенка скважины является внутренней границей пласта.

Начальные условия позволяют определить характеристики системы флюид - пористая среда в некоторый момент времени, задаваясь искомой функцией.

Например, давление на контуре питания (рк) или в скважине (рс) в начальный момент времени, т.е. при t=0.Искомой функцией является пластовое давление, тогда начальное

условие может иметь вид: P=Po(XYZ) при t=0, т.е. задается распределение давления во всем пласте в начальный момент.

Если в начальный момент пласт не возмущен, то начальное условие примет вид: P=Pk=const при t=0.

Граничные условия, число которых должно быть равно порядку дифференциального уравнения по координатам, задается для характеристики параметров процесса на границах пласта (внешние) и на забое скважине (внутренние).

 

 

БИЛЕТ № 22