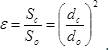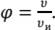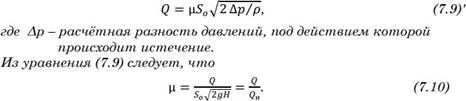Билет 1
Билет 2
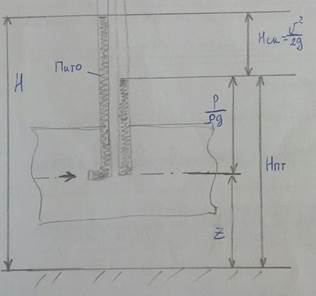
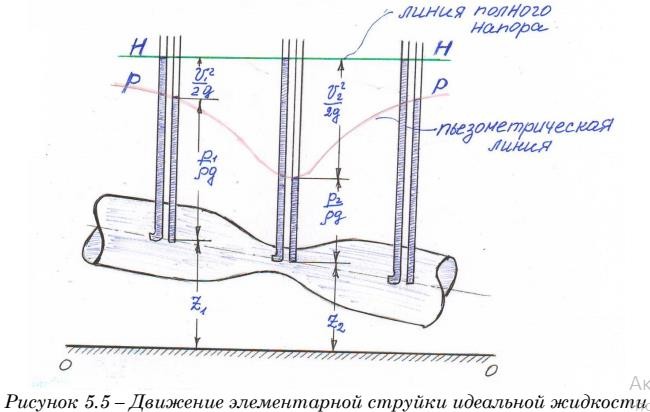
1. Уравнение Бернулли для установившегося движения элементарной струйки идеальной жидкости: графическое представление, интерпретация с геометрической точки зрения.
𝑧 +
𝑝1
𝜗2
+ = 𝑧
+ 𝑝2
𝜗2
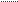
+
 1 𝜌𝑔
1 𝜌𝑔
2𝑔
2 𝜌𝑔
2𝑔
𝑧1
+ 𝑝
 𝜌𝑔
𝜌𝑔
= 𝐻пт
-потенциальный напор
𝑧1, 𝑧2 –геометрический напор представляет собой геометрическую высоту, или геометрический напор, т.е. измеряет высоту расположения
движущейся частицы жидкости в данном сечении над некоторой горизонтальной плоскостью - плоскостью сравнения
𝑝 1 , 𝑝 2 –пьезометрический напор. так же пьезометрическая высота, т.е.
𝜌𝑔 𝜌𝑔
представляет высоту столба жидкости, уравновешивающуюся давление р в данной точке.
𝜗2 𝜗2
1 , 2 -скоростная высота, или скоростной напор. Даѐт ту высоту, с которой должно свободно
2𝑔 2𝑔
упасть тело, чтобы, падая в пустоте, в конце пути приобрести скорость υ. Уровень жидкости в трубке Пито устанавливается выше уровня жидкости в пьезометрической трубке как раз на
величину 𝐻ск
= 𝜗2. Эта высота тем больше, чем больше скорость в данном сечении, так что
 2𝑔
2𝑔
по величине скоростного напора можно судить и о скорости. Итак, геометрический смысл уравнения Бернулли можно сформулировать так: при установившемся движении идеальной жидкости сумма трѐх напоров (высот) – геометрического, пьезометрического и скоростного вдоль струйки остаѐтся неизменной.
Причины нарушения закона Дарси и пределы его применимости.

Наиболее полно изучены отклонения от закона Дарси, вызванные
проявлением инерционных сил при увеличении скорости фильтрации. Изначально, по аналогии с трубопроводной гидравликой, было высказано предположение, что при некоторых скоростях фильтрации происходит переход от ламинарного режима фильтрации к турбулентному. И, следовательно, именно турбулизация потока вызывает отклонения от линейной зависимости.
Первая количественная оценка верхней границы применимости закона Дарси была предложена Н.Н. Павловским, который вывел следующую формулу для определения фильтрационного числа Рейнольдса:
𝑅𝑒 = 𝑊 𝑑 э ф
ν(0,75m+0,23)
,где
W- скорость фильтрации
𝑑эф- характерный фильтрационный линейный размер
m- пористость
ν- кинематическая вязкость
Н.Н. Павловский установил, что критические значения числа Re находятся в пределах - Reкр=7,5÷9.
Дальнейшее конструирование формул для фильтрационного числа
Рейнольдса было проделано М.Д. Миллионщиковым:

𝜗√𝑘/𝑚 ∗ 𝜌

 𝜌𝑊√𝑘
𝜌𝑊√𝑘
𝑑эф

 = √ 𝑘
= √ 𝑘
𝑚
𝑅𝑒 =
 - внутренний масштаб породы
- внутренний масштаб породы
𝜇 = μm1,5
 𝜗 = 𝑊
𝜗 = 𝑊
𝑚
При этом критическое значение числа Rе колеблется в пределах -
0,022≤Reкр≤0,29.
Иное выражения для определения фильтрационного числа Рейнольдса было предложено в 1942 г. В.Н. Щелкачевым, формула
которого объединяет в себе оба рассмотренных выше подхода как Н.Н.Павловского, так и М.Д. Миллионщикова, и имеет вид:
10𝑊√𝑘
 𝑅𝑒 = 𝜈 ∙ 𝑚2,3
𝑅𝑒 = 𝜈 ∙ 𝑚2,3
критические значения лежат в
интервале - 1≤Reкр≤12.
БИЛЕТ 3
1. Уравнения неразрывности для элементарной струйки и потока жидкости.
Рассмотрим элементарную струйку, имеющую бесконечно малые поперечные сечения dS и одинаковую для всех точек сечения скорость движения жидкости
За время dt частицы жидкости, находящиеся в сечении 1-1 переместятся вдоль элементарной струйки на расстоянии dl, равное:
dl = u ∙ dt.
Следующие за ними другие частицы заполняют все освобождаемое пространство, и поэтому за время dt через сечение струйки 1-1 пройдет объем жидкости dV, равный:
dV = dS ∙ dl = dS ∙ u ∙ dt.
v1dQ1 = v2dQ2 = v3dQ3 = ⋯ = vndQn = vdQ = const.
Это и есть уравнение неразрывности (сплошности) для элементарной струйки, которое читается так: Элементарный расход несжимаемой жидкости при установившемся движении есть величина постоянная вдоль всей элементарной струйки.
vср1Q1 = vср2Q2 = vср3Q3 = ⋯ = vсрnQn = vсрQ = const,
Это и есть уравнение неразрывности для потока жидкости,которое читается так: Расход
несжимаемой жидкости через любое живое сечение потока при установившемся движении есть величина постоянная вдоль всего потока.
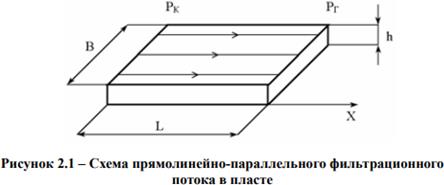
2. Схемы одномерных фильтрационных потоков: основные понятия, характеристики.
1. Прямолинейно-параллельный поток. Траектории всех частиц жидкости - параллельные
прямые, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока равны между собой, поверхности равных потенциалов (эквипотенциальные поверхности) и поверхности равных скоростей (изотахи) являются плоскими поверхностями
перпендикулярными траекториям.
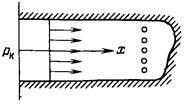
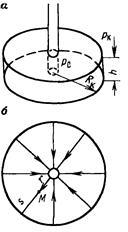
2. Плоскорадиальный поток. Траектории всех частиц жидкости - прямолинейные горизонтальные прямые, радиально сходящиеся к центру скважины, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока параллельны и равны между
собой; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют
цилиндрические окружности с осью, совпадающей с осью скважины. Схемы линий тока в любой горизонтальной плоскости потока будут идентичными и для характеристики потока достаточно рассмотреть движение жидкости в одной горизонтальной плоскости.
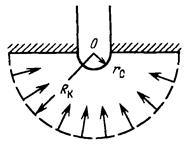
3.Радиально-сферический поток.Траектории всех частиц жидкости - прямолинейные
горизонтальные прямые, радиально сходящиеся к центру полусферического забоя; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют сферические
поверхности.
БИЛЕТ 4
Билет
Билет 6
Билет 7
Билет 8
Билет № 9
БИЛЕТ № 10
Билет 11
БИЛЕТ 12
1. Гидравлические сопротивления в трубопроводах, виды потерь напора, определения, расчетные формулы.
Гидравлическими сопротивлениями называются все внешние факторы при движении потока реальной жидкости, которые обуславливают потери некоторой части еѐ механической энергии. Потери напора по длине потока, связанные с преодолением сопротивления сил трения при равномерном или плавно изменяющемся неравномерном движении называются потерями
напора по длине или линейными потерями.
Местными потерями напора называются потери напора на отдельных коротких участках потока жидкости в результате деформации и возникновения вихреобразований (обозначаются - hм).
На основании экспериментальных данных величину местных потерь напора Вейсбах предложил определять в зависимости от скоростного напора по формуле:
𝑣^2
ℎ = ξ ∙

2𝑔
где ξ - безразмерный коэффициент, называемый коэффициентом местного сопротивления;
υ - средняя скорость в живом сечении, как правило, непосредственно за местным сопротивлением;
Основной расчѐтной формулой для определения линейных потерь в круглых трубах является формула Дарси-Вейсбаха:
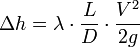 выраженная через скорость hтр = λ выраженная через расход hтр = λ ℎ =
выраженная через скорость hтр = λ выраженная через расход hтр = λ ℎ =
 𝑙 ∙
𝑙 ∙
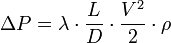 𝑑
𝑑
8𝑄^2

𝑔п^2𝑑^4
или в единицах давления ∆pтр = λ
где λ – коэффициент гидравлического трения; l – длина трубы;
d – внутренний диаметр трубы.
При ламинарном режиме, Re<2300, коэффициент гидравлического трения λ определяется по формуле Стокса: 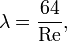
Таким образом, коэффициент гидравлического трения λ при ламинарном режиме зависит только от числа Re, обратно пропорционален этому числу и не зависит от шероховатости стенки трубы. В переходной зоне, или зоне шероховатых труб, при 20d/ ∆< Re<500 d/∆, коэффициент трения
зависит от обеих характеристик и определяется по формуле Альтшуля: λ = 0,11 (∆ / d + 68 / Re)^0,25
При Re > 500 d/∆ Поскольку ламинарного слоя нет, коэффициент λ уже не зависит от числа Re, поэтому эта зона названа зоной вполне шероховатых труб. В этой зоне коэффициент λ
определяется по формуле Шифринсона: λ = 0,11 (∆ / d)^0,25
БИЛЕТ 13
Билет 14
Одномерным
Слоисто – неоднородный пласт:
Распределение давления в пропластках:
𝑃(𝑥) = 𝑃𝑘
− 𝑃𝑘 − 𝑃г 𝑥
 𝐿
𝐿
0≤x≤L
где Р(х) – давление в произвольной точке Х пласта, Па (1 Па = 1 Н/м2);
Pк и Pг – заданное давление на контуре питания и галерее соответственно, Па; Lк – длина пласта, м;
x –координата точки пласта, отсчитываемая от контура питания, м.
Массовый расход i – го пропластка:
𝑄 = 𝑘𝑖 ρ

𝑘𝑖 (𝑃𝑘 − 𝑃г) 𝐵ℎ

Массовый расход пласта
𝑚𝑖 𝜇 0
𝜇𝐿 𝑖
𝑛
𝑄𝑚
= ρ0
𝐵(𝑃𝑘 − 𝑃г) ∑ ℎ
 𝜇𝐿 𝑖
𝜇𝐿 𝑖
𝑖=1
𝑘𝑖
Скорость фильтрации в пропластке
𝑊𝑖
= 𝑘𝑖 (𝑃𝑘 − 𝑃г)
 𝜇𝐿
𝜇𝐿
Время движения частиц в i – ом пропластке
𝑡𝑖
= 𝑚𝑖 𝜇𝑥𝐿
 𝑘𝑖 (𝑃𝑘 − 𝑃г)
𝑘𝑖 (𝑃𝑘 − 𝑃г)
Билет 15
1.
Уравнение Бернулли для установившегося движения элементарной струйки реальной жидкости: графическое представление, интерпретация с геометрической точки зрения.
Билет 16
Билет 17
Билет 18
Определения дебита гидродинамически несовершенной скважины по степени и по характеру вскрытия с помощью графиков В.И. Щурова.
Дебит несовершенных скважин определяется по формуле
где С1, С2 - безразмерные коэффициенты.
Коэффициент С1, учитывающий дополнительное фильтрационное сопротивление в призабойной зоне пласта из-за несовершенства скважины по степени вскрытия, зависит только от
относительного вскрытия пласта ℎ̅ и отношения толщины пласта к диаметру скважины h/Dс.
Для определения C1 по графику В.И. Щурова необходимо: по значению h/Dс выбрать номер линии на графике, по степени вскрытия пласта ℎ̅ найти C1
Коэффициент С2, учитывающий дополнительное фильтрационное сопротивление в призабойной зоне пласта из-за несовершенства скважины по характеру вскрытия, зависит от диаметра
перфорационного канала dп, числа отверстий на один метр длины скважины nп и длины перфорационного канал lп.
Для определения C2 по графикам В.И. Щурова: по значению lп/Dc находится график, по которому находится С2, по значению dп/Dc находится номер линии на этом графике, по значению nп Dc
находится значение С2
БИЛЕТ 19
1. Режимы течения жидкости в трубах: основные понятия, расчетные формулы.
При изучении движения вязкой жидкости различают два режима - ламинарный и турбулентный.
Ламинарным называется режим движения жидкости имеющий слоистый характер, когда струйки жидкости в потоке движутся с
различными скоростями параллельно оси трубы без перемешивания.
Турбулентным называется режим движения жидкости
характеризующийся беспорядочным, хаотическим движением жидких частиц, с более или менее интенсивным перемешиванием их в потоке.
Экспериментальные исследования показали, что от режима движения жидкости существенно зависят потери энергии в потоке на преодоление сопротивлений по длине, поэтому изучение режимов и закономерностей их определяющих, имеет большое практическое
значение.
Характеристикой режимов движения служит безразмерное
число Рейнольдса, названное в честь О. Рейнольдса, который обобщив результаты опытов с различными жидкостями, движущимися с разными скоростями по трубам различных диаметров, получил
критерий, составленный из величин, характеризующих поток жидкости.
Для напорной трубы круглого сечения число Рейнольдса записывается в виде:
Число Рейнольдса соответствующее смене режима (переходу из ламинарного режима в турбулентный, или, наоборот, из турбулентного в ламинарный), называется критическим.
Для движения жидкости в напорных трубах круглого сечения
критическое значение числа Рейнольдса следует считать равным Reкр = 2320.
При значениях Re < Reкр - режим движения жидкости будет ламинарным, при Re > Reкр - турбулентным.
Скорость движения жидкости, при которой происходит смена
режимов, называется критической скоростью.
В отличие от критического значения числа Рейнольдса, одинакового для потока любой жидкости в трубопроводе любого диаметра,
критическая скорость для каждой жидкости имеет своё определённой значение, зависящее от диаметра трубопровода и коэффициента
вязкости жидкости:
Характер движения частиц при ламинарном и турбулентном режимах различен. При ламинарном режиме частицы жидкости
перемещаются как бы слоями по траекториям, параллельным между собой. При турбулентном режиме траектория движения частиц
криволинейна и сложна. Частицы жидкости при движении
сталкиваются между собой, и происходит довольно интенсивный процесс перемещения.
Движение жидких частиц можно сделать видимым, окрасив поток. Таким образом, установить режим движения жидкости можно двумя методами:
- определением числа Рейнольдса
- и визуальным методом, наблюдая за движением частиц в подкрашенном потоке.
Если краска, добавленная к потоку, располагается в виде прямой
струйки, отчётливо видной на всём протяжении, это свидетельствует о параллельном перемещении частиц жидкости или о наличии
ламинарного режима движения. При этом число Рейнольдса оказывается меньше критического значения, т.е. меньше 2320.
Если струйка размывается потоком и равномерно окрашивает его,
это свидетельствует о движении частиц по сложным траекториям, что
приводит к перемешиванию, или о наличии турбулентного режима. При этом число Рейнольдса – больше критического, т.е. больше 2320.
БИЛЕТ № 20
Билет 21
БИЛЕТ № 22
Билет 23
1. Истечение жидкости через насадки. Основные расчётные формулы Насадок представляет собой короткую трубу, приставленную к отверстию.
Различают следующие наиболее распространѐнные типы насадков.
-цилиндрические – внешний и внутренний;
- конические – сходящиеся и расходящиеся;
-коноидальные, т.е. криволинейного очертания, имеющие форму сжатой струи.
К устройству насадков прибегают для увеличения пропускной
способности отверстия и для увеличения или уменьшения кинетической энергии струи.
При протекании жидкости через насадки скорость и расход
определяются использованием тех же формул, что и для отверстий в тонкой стенке, но с иными значениями коэффициентов скорости φ и расхода μ для каждого типа насадка.
Объѐмный расход жидкости, вытекающей из отверстия,
определяется как произведение действительной скорости истечения на площадь струи в сжатом сечении, а с учѐтом соотношений
𝑄 = 𝑆с𝜐 = 𝜀𝜑𝑆𝑜 √2𝑔𝐻. где 𝜐 = 𝜑√2𝑔𝐻
Произведение коэффициентов ε и φ принято обозначать буквой μ и называть коэффициентом расхода, т.е. 𝜇 = 𝜀𝜑.
Тогда окончательно формула (7.7) записывается как
𝑄 = 𝜇𝑆𝑜√2𝑔𝐻

Или 𝑄 = 𝜇𝑆𝑜√2 ∆𝑝/𝜌 где Δp – расчѐтная разность давлений, под действием которой происходит истечение.
Из уравнения следует, что
Таким образом, коэффициент расхода - μ показывает, насколько действительный расход жидкости при истечении из отверстия
уменьшается по сравнению с тем расходом - Qи, который имел бы место при отсутствии сжатия струи и сопротивления.
Билет 24
Билет 25
Несжимаемой жидкости
Введение функции Лейбензона в уравнения позволяет установить аналогию между установившейся фильтрацией сжимаемого флюида и установившейся фильтрацией несжимаемой жидкости.
В дальнейшем принимаем, что проницаемость среды и динамический коэффициент вязкости флюида постоянны, т.е. k=const и m=const, а плотность флюида r=r(Р). Тогда можно ввести функцию Лейбензона как
при этом
R = ò r (P) dP + C , (6.11)

 d R = r (R) d R. (6.12)
d R = r (R) d R. (6.12)
 Запишем закон Дарси для установившейся фильтрации несжимаемой жидкости в дифференциальной форме (1.15) через расход
Запишем закон Дарси для установившейся фильтрации несжимаемой жидкости в дифференциальной форме (1.15) через расход
где Q=const; w(S) - площадь поперечного сечения струйки.
, (6.13)
При установившейся фильтрации сжимаемого флюида по всей длине струйки массовыйрасход сохраняется постоянным:
Qm= rQ = const.
 Умножив обе части равенства (6.13) на плотность флюида r(Р) и используя соотношение (6.12), имеем
Умножив обе части равенства (6.13) на плотность флюида r(Р) и используя соотношение (6.12), имеем
, Qm =const. (6.14)
 Легко видеть, что выражения (6.13) и (6.14) являются однотипными дифференциальными уравнениями, в которых объемному расходу Q несжимаемой жидкости соответствует массовый расход Qm сжимаемого флюида, а давлению в уравнении (6.13) соответствует функция Лейбензона R в уравнении (6.14).
Легко видеть, что выражения (6.13) и (6.14) являются однотипными дифференциальными уравнениями, в которых объемному расходу Q несжимаемой жидкости соответствует массовый расход Qm сжимаемого флюида, а давлению в уравнении (6.13) соответствует функция Лейбензона R в уравнении (6.14).
Уравнения движения (6.2) для несжимаемой жидкости связывают скорость фильтрации V
 с давлением Р, а для сжимаемого флюида – массовую скорость фильтрации r V c функцией Лейбензона R в уравнениях (6.6).
с давлением Р, а для сжимаемого флюида – массовую скорость фильтрации r V c функцией Лейбензона R в уравнениях (6.6).
 Отсюда вывод (аналогия): все формулы, полученные для установившейся фильтрации несжимаемой жидкости по закону Дарси, можно использовать и для установившейся фильтрации сжимаемого флюида в пластах той же геометрии и при тех же граничных условиях, заменив соответствующие параметры:
Отсюда вывод (аналогия): все формулы, полученные для установившейся фильтрации несжимаемой жидкости по закону Дарси, можно использовать и для установившейся фильтрации сжимаемого флюида в пластах той же геометрии и при тех же граничных условиях, заменив соответствующие параметры:
| Несжимаемая жидкость
| Сжимаемый флюид
|
| Объемный расход – Q Давление - Р
Объемная скорость фильтрации - V
| Массовый расход - Qm Функция Лейбензона - R
Массовая скорость фильтрации - r V
|
При этом помним, что при фильтрации сжимаемого флюида под давлением Р понимается абсолютное давление.
БИЛЕТ № 26
Билет 27
Билет 28
Билет 29.
Основные понятия о струйчатом движении жидкости
Выделим в пространстве движущейся жидкости частицу жидкости. За определенный промежуток времени частица пройдет через ряд точек пространства с различными
скоростями. След, оставленный частицей в виде кривой линии, является траекторией
движения. При установившемся движении скорость в каждой точке траектории является неизменной во времени, а траектории отдельных частиц также являются во времени неизменными кривыми. При установившемся движении поле скоростей в
рассматриваемом пространстве остается неизменным с течением времени.
В случае неустановившегося движения частица при прохождении точки в разное время имеет разные скорости
 Выберем в пространстве, занятом движущейся жидкостью, в некоторый момент времени т. 1, через которую пройдет частица жидкости. Построим к точке вектор
Выберем в пространстве, занятом движущейся жидкостью, в некоторый момент времени т. 1, через которую пройдет частица жидкости. Построим к точке вектор

 скорости , который определяет направление движения частицы и ее скорость. На этом векторе, отложив малое расстояние , получим т. 2
скорости , который определяет направление движения частицы и ее скорость. На этом векторе, отложив малое расстояние , получим т. 2
 Полученная кривая, начинающаяся в
Полученная кривая, начинающаяся в
т. 1, является линией тока.

 Кривая, проведенная через ряд точек жидкости при установившемся ее движении, в каждой точке которой в данный момент времени векторы скорости касательные,
Кривая, проведенная через ряд точек жидкости при установившемся ее движении, в каждой точке которой в данный момент времени векторы скорости касательные,
называется линией тока. Линия тока в другой промежуток времени при неустановившемся движении будет представлять другую кривую.
Выделим в пространстве движущейся жидкости элементарный замкнутый контур и через все его точки проведем линии тока. Образовавшаяся таким образом трубчатая
поверхность называется трубкой тока. Трубка тока представляет собой как бы бесконечно тонкую непроницаемую стенку.
Частички жидкости, движущиеся внутри трубки тока, образуют элементарную струйку жидкости. В случае стремления поперечных сечений струйки жидкости к нулю она в
пределе будет обращаться в линию тока.
Билет 30
Основные понятия гидродинамики: гидродинамическое давление, скорость движения жидкости. Виды движения
Гидродинамическое давление, p – это внутреннее давление (нормальное напряжение сжатия), возникающее при движении жидкости.
Скорость движения жидкости в данной точке, v- это скорость перемещения в пространстве,
находящейся в данной точке, частицы жидкости, определяемая длиной пути l, пройденного этой частицей за единицу времени t.
В общем случае основные элементы движения жидкости p и v для данной точки зависят от ее
положения в пространстве (координат точки) и могут изменяться во времени. Аналитически это положение гидродинамики записывается так:
p = f1 (x,y,z,t); v = f2 (x,y,z,t).
Основная трудность изучения законов движения жидкости обусловлена самой природой
жидкости, особенно сложностью учета сил трения. По предложению Л. Эйлера удобнее начинать с рассмотрения идеальной жидкости, т.е. линейной вязкости, и однородной, т.е. имеющей
постоянную во всех точках плотность. А затем вносить в найденные уравнения поправки для учета сил трения реальных жидкостей. Виды движения жидкости Движение жидкости может быть
установившимся и неустановившимся.
Неустановившимся называется движение жидкости, все характеристики которого (или некоторые из них) в точках потока изменяются с течением времени.
Примером неустановившегося движения может являться истечение (опорожнение) жидкости из резервуара при переменном напоре, или движение жидкости в трубопроводе, создаваемое работой поршневого насоса, поршень которого совершает возвратно- поступательное движение
(рис. 4.4). 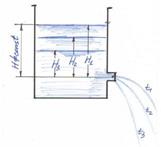
Рисунок 4.4 - Пример неустановившегося движения жидкости
Установившимся называется такое движение жидкости, при котором параметры потока не изменяются с течением времени.
Примером установившегося движения жидкости является истечение жидкости из резервуара, (при постоянном напоре) в котором поддерживается постоянный уровень, или движение
жидкости в трубопроводе, создаваемое работой центробежного насоса с постоянной частотой вращения (рис.4.5).
Рисунок 4.5 - Пример установившегося движения жидкости
Исследование установившегося движения гораздо проще неустановившегося. Поэтому в дальнейшем будет рассматриваться, главным образом, установившееся движение и лишь некоторые частные случаи неустановившегося.
Установившееся движение может быть равномерным и неравномерным.
Равномерным называется установившееся движение жидкости, если значения скоростей в соответствующих точках любых живых сечений будут одинаковы и поле скоростей остается неизменным вдоль потока.
Примером равномерного движения можно считать движение жидкости в трубе постоянного
поперечного сечения или канале неизмененного сечения (напр., трапецеидального) и постоянной глубины (рис. 4.6)
Рисунок 4.6 – Пример равномерного движения
Неравномерным называется установившееся движение, если сечение потока по длине будет непостоянным, или расход жидкости будет изменяться по длине потока вследствие притока со стороны или утечки жидкости по пути течения.
Примером неравномерного движения можно считать движение в конической трубе или в естественных условиях (рис. 4.7).
Рисунок 4.7 - Пример неравномерного движения
В зависимости от условий, при которых происходит движение, различается напорное и безнапорное движение.
Напорный поток полностью ограничен со всех сторон твердыми стенками. Движение жидкости в таком потоке происходит под влиянием давления, сообщаемого каким-либо внешним
источником.
Примером напорного движения является движение воды в водопроводной трубе.
Безнапорным называется поток со свободной поверхностью, в котором жидкости перемещается только под действием силы тяжести.
Примером безнапорного движения является движение воды в реках и каналах.
Билет 31
Билет 32
1.Гидравлические элементы потока: определения, расчетные формулы.
Живым сечением потока называется поверхность, к каждой точке которой линии тока направлены по нормали. Площадь живого сечения будем обозначать ω.Длина контура живого сечения, по
которому поток соприкасается с ограничивающими его стенками, называется смоченным периметром, X
периметр смачивания: X = b + 2h,
Отношение площади живого сечения к смоченному периметру называется гидравлическим радиусом сечения, т.е.
R =ω/X
геометрический радиус r =d/2
Расходом жидкости называют количество жидкости,
протекающее через поперечное сечение потока в единицу времени. Это количество можно выразить в единицах объема, в весовых
единицах или в единицах массы, в связи с чем, различают:
- объемный Q =V/t; - весовой QG =G/t; - массовый Qm =m/t Единицами расхода являются: - объѐмного в СИ м3/с, в СГС м3/с (1л/с=0,001м3/с; 1м/с=1000см3/с); - весового в СИ Н/с;
- массового в СИ кг/с, в СГС г/с.
Между объемным, массовым и весовым расходом существует взаимосвязь: Q =Qm/ρ=QG/γ Средняя скорость потока в данном сечении, представляющая собой частное от расхода Q на площадь живого сечения потока: v =Q/ω
Средняя скорость в сечении представляет собой одинаковую для всех точек сечения воображаемую скорость, при которой через данное сечение проходит тот же расход, что и при действительных местных скоростях, разных в различных точках сечения.
БИЛЕТ № 33
Билет 34
Выраженная через скорость
Выраженная через расход
𝑙 𝑣2
 ℎтр = 𝜆 𝑑 2𝑔
ℎтр = 𝜆 𝑑 2𝑔
 𝑙 8𝑄2
𝑙 8𝑄2
Или в единицах давления
ℎтр = 𝜆 𝑑 𝑔𝜋2𝑑4
𝑙 ρ𝑣2
 𝛥𝑝тр = 𝜆 𝑑 2
𝛥𝑝тр = 𝜆 𝑑 2
𝜆 – коэффициент гидравлического трения;
l – длина трубы;
d – внутренний диаметр трубы.
Местными потерями напора называются потери напора на отдельных коротких участках
потока жидкости в результате деформации и возникновения вихреобразований (обозначаются -
𝒉м).
Местные сопротивления – гидравлические сопротивления, возникающие в результате
деформации потока жидкости на отдельных его участках. При деформации происходит
изменение характера движения, связанного с направлением и величиной скорости потока, а затем восстановление его.
Например, деформация потока происходит в результате перемены направления движения на участке трубопровода или изменения площади живого сечения.
В результате деформации потока на местном участке трубопровода происходит достаточно резко изменяющееся неравномерное движение с вихреобразованием. Длина местного
сопротивления является весьма малой по сравнению с длиной всего потока и поэтому потери напора по длине в нѐм существенно малы.
В потоке жидкости возникают как потери по длине, так и местные потери. Полные потери
напора при движении жидкости в трубопроводе с участками, где происходит деформация потока, можно выразить как
𝒉 = 𝒉л + ∑ 𝒉м
где ∑ 𝒉м - сумма местных потерь напора;
𝒉л- потери напора по длине.
На основании экспериментальных данных величину местных потерь напора Вейсбах
предложил определять в зависимости от скоростного напора по формуле:
𝑣2
 ℎм = 𝜉 2𝑔
ℎм = 𝜉 2𝑔
Или
𝛥𝑝м = 𝜉
ρ𝑣2

2
ξ - безразмерный коэффициент, называемый коэффициентом местного сопротивления;
υ - средняя скорость в живом сечении, как правило, непосредственно за местным сопротивлением;
ρ – плотность жидкости.
Билет 1
Истечение жидкости через отверстие в тонкой стенке. Основные расчётные формулы.
Истечение жидкости через отверстие может происходить при постоянном и переменном напоре. Если истечение жидкости через отверстие происходит в атмосферу или другую газовую среду, то такое отверстие называется незатопленным. Если же истечение идет под уровень, а не в
атмосферу – затопленным.
При истечении струи в атмосферу из малого отверстия в тонкой стенке происходит изменение формы струи по ее длине, называемое инверсией струи. Обуславливается это явление в основном действием сил поверхностного натяжения на вытекающие криволинейные струйки и различными условиями сжатия по периметру отверстия. Инверсия больше всего проявляется при истечении из некруглых отверстий.
Степень сжатия струи оценивается коэффициентом сжатия ε, равным отношению площади поперечного сечения струи к площади отверстия
Значение коэффициента сжатия зависит от характера сжатия,которое бывает совершенным и несовершенным, а также полным и неполным. Значение коэффициента сжатия зависит от
характера сжатия, которое бывает совершенным и несовершенным, а также полным и неполным.
В обычных условиях при истечение воды из больших резервуаров через малое отверстие
наблюдается полное совершенное сжатие, при котором значение коэффициента сжатия струи находится в пределах ε = 0, 60... 0, 64.
Определить скорость истечения жидкости через малое отверстие в тонкой стенке можно составив уравнение Бернулли для двух сечений: сечения 1-1 на свободной поверхности жидкости в резервуаре, где давление р0, а скорость можно считать равной нулю и сечения 2-2 - сжатое
сечение струи, где давление соответствует давлению р1 окружающей среды.
Коэффициент скорости – φ есть отношение действительной скорости истечения к скорости идеальной жидкости
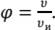

Коэффициент расхода - μ показывает, насколько действительный расход жидкости при истечении из отверстия уменьшается по сравнению с тем расходом - Qи, который имел бы место при отсутствии сжатия струи и сопротивления.
2. Приток несжимаемой жидкости к галерее в неоднородном по толщине пл





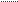
 1 𝜌𝑔
1 𝜌𝑔
 𝜌𝑔
𝜌𝑔 2𝑔
2𝑔


 𝜌𝑊√𝑘
𝜌𝑊√𝑘
 = √ 𝑘
= √ 𝑘 - внутренний масштаб породы
- внутренний масштаб породы 𝜗 = 𝑊
𝜗 = 𝑊
 𝑅𝑒 = 𝜈 ∙ 𝑚2,3
𝑅𝑒 = 𝜈 ∙ 𝑚2,3

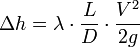 выраженная через скорость hтр = λ выраженная через расход hтр = λ ℎ =
выраженная через скорость hтр = λ выраженная через расход hтр = λ ℎ = 𝑙 ∙
𝑙 ∙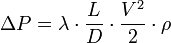 𝑑
𝑑
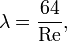

 𝐿
𝐿

 𝜇𝐿 𝑖
𝜇𝐿 𝑖 𝜇𝐿
𝜇𝐿










 d R = r (R) d R. (6.12)
d R = r (R) d R. (6.12) Запишем закон Дарси для установившейся фильтрации несжимаемой жидкости в дифференциальной форме (1.15) через расход
Запишем закон Дарси для установившейся фильтрации несжимаемой жидкости в дифференциальной форме (1.15) через расход Умножив обе части равенства (6.13) на плотность флюида r(Р) и используя соотношение (6.12), имеем
Умножив обе части равенства (6.13) на плотность флюида r(Р) и используя соотношение (6.12), имеем Легко видеть, что выражения (6.13) и (6.14) являются однотипными дифференциальными уравнениями, в которых объемному расходу Q несжимаемой жидкости соответствует массовый расход Qm сжимаемого флюида, а давлению в уравнении (6.13) соответствует функция Лейбензона R в уравнении (6.14).
Легко видеть, что выражения (6.13) и (6.14) являются однотипными дифференциальными уравнениями, в которых объемному расходу Q несжимаемой жидкости соответствует массовый расход Qm сжимаемого флюида, а давлению в уравнении (6.13) соответствует функция Лейбензона R в уравнении (6.14). с давлением Р, а для сжимаемого флюида – массовую скорость фильтрации r V c функцией Лейбензона R в уравнениях (6.6).
с давлением Р, а для сжимаемого флюида – массовую скорость фильтрации r V c функцией Лейбензона R в уравнениях (6.6). Отсюда вывод (аналогия): все формулы, полученные для установившейся фильтрации несжимаемой жидкости по закону Дарси, можно использовать и для установившейся фильтрации сжимаемого флюида в пластах той же геометрии и при тех же граничных условиях, заменив соответствующие параметры:
Отсюда вывод (аналогия): все формулы, полученные для установившейся фильтрации несжимаемой жидкости по закону Дарси, можно использовать и для установившейся фильтрации сжимаемого флюида в пластах той же геометрии и при тех же граничных условиях, заменив соответствующие параметры: Выберем в пространстве, занятом движущейся жидкостью, в некоторый момент времени т. 1, через которую пройдет частица жидкости. Построим к точке вектор
Выберем в пространстве, занятом движущейся жидкостью, в некоторый момент времени т. 1, через которую пройдет частица жидкости. Построим к точке вектор
 скорости , который определяет направление движения частицы и ее скорость. На этом векторе, отложив малое расстояние , получим т. 2
скорости , который определяет направление движения частицы и ее скорость. На этом векторе, отложив малое расстояние , получим т. 2 Полученная кривая, начинающаяся в
Полученная кривая, начинающаяся в
 Кривая, проведенная через ряд точек жидкости при установившемся ее движении, в каждой точке которой в данный момент времени векторы скорости касательные,
Кривая, проведенная через ряд точек жидкости при установившемся ее движении, в каждой точке которой в данный момент времени векторы скорости касательные,



 ℎтр = 𝜆 𝑑 2𝑔
ℎтр = 𝜆 𝑑 2𝑔 𝑙 8𝑄2
𝑙 8𝑄2 𝛥𝑝тр = 𝜆 𝑑 2
𝛥𝑝тр = 𝜆 𝑑 2 ℎм = 𝜉 2𝑔
ℎм = 𝜉 2𝑔