Причины нарушения закона Дарси и пределы его применимости.

Наиболее полно изучены отклонения от закона Дарси, вызванные

проявлением инерционных сил при увеличении скорости фильтрации. Изначально, по аналогии с трубопроводной гидравликой, было высказано предположение, что при некоторых скоростях фильтрации происходит переход от ламинарного режима фильтрации к турбулентному. И, следовательно, именно турбулизация потока вызывает отклонения от линейной зависимости.

Первая количественная оценка верхней границы применимости закона Дарси была предложена Н.Н. Павловским, который вывел следующую формулу для определения фильтрационного числа Рейнольдса:

𝑅𝑒  =    𝑊 𝑑 э ф   

ν(0,75m+0,23)

,где

W- скорость фильтрации

𝑑эф- характерный фильтрационный линейный размер

m- пористость

ν- кинематическая вязкость

Н.Н. Павловский установил, что критические значения числа Re находятся в пределах - Reкр=7,5÷9.

Дальнейшее конструирование формул для фильтрационного числа

Рейнольдса было проделано М.Д. Миллионщиковым:

 

𝜗√𝑘/𝑚 ∗ 𝜌

 

𝜌𝑊√𝑘

 

 

𝑑эф

 

 

= √ 𝑘

𝑚

𝑅𝑒 =

 

- внутренний масштаб породы

𝜇   = μm1,5

𝜗 = 𝑊

𝑚

При этом критическое значение числа Rе колеблется в пределах -

0,022≤Reкр≤0,29.

Иное выражения для определения фильтрационного числа Рейнольдса было предложено в 1942 г. В.Н. Щелкачевым, формула

которого объединяет в себе оба рассмотренных выше подхода как Н.Н.Павловского, так и М.Д. Миллионщикова, и имеет вид:

10𝑊√𝑘

𝑅𝑒 = 𝜈 ∙ 𝑚2,3

критические значения лежат в

интервале - 1≤Reкр≤12.

 

БИЛЕТ 3

1. Уравнения неразрывности для элементарной струйки и потока жидкости.

Рассмотрим элементарную струйку, имеющую бесконечно малые поперечные сечения dS и одинаковую для всех точек сечения скорость движения жидкости

За время dt частицы жидкости, находящиеся в сечении 1-1 переместятся вдоль элементарной струйки на расстоянии dl, равное:

dl = u ∙ dt.

Следующие за ними другие частицы заполняют все освобождаемое пространство, и поэтому за время dt через сечение струйки 1-1 пройдет объем жидкости dV, равный:

dV = dS ∙ dl = dS ∙ u ∙ dt.

v1dQ1 = v2dQ2 = v3dQ3 = ⋯ = vndQn = vdQ = const.

Это и есть уравнение неразрывности (сплошности) для элементарной струйки, которое читается так: Элементарный расход несжимаемой жидкости при установившемся движении есть величина постоянная вдоль всей элементарной струйки.

vср1Q1 = vср2Q2 = vср3Q3 = ⋯ = vсрnQn = vсрQ = const,

Это и есть уравнение неразрывности для потока жидкости,которое читается так: Расход

несжимаемой жидкости через любое живое сечение потока при установившемся движении есть величина постоянная вдоль всего потока.

2. Схемы одномерных фильтрационных потоков: основные понятия, характеристики.

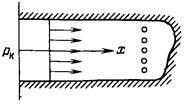
1. Прямолинейно-параллельный поток. Траектории всех частиц жидкости - параллельные

прямые, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока равны между собой, поверхности равных потенциалов (эквипотенциальные поверхности) и поверхности равных скоростей (изотахи) являются плоскими поверхностями

перпендикулярными траекториям.

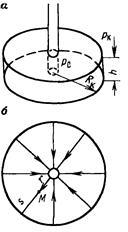2. Плоскорадиальный поток. Траектории всех частиц жидкости - прямолинейные горизонтальные прямые, радиально сходящиеся к центру скважины, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока параллельны и равны между

собой; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют

цилиндрические окружности с осью, совпадающей с осью скважины. Схемы линий тока в любой горизонтальной плоскости потока будут идентичными и для характеристики потока достаточно рассмотреть движение жидкости в одной горизонтальной плоскости.

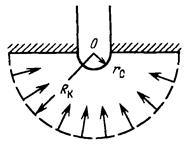
3.Радиально-сферический поток.Траектории всех частиц жидкости - прямолинейные

горизонтальные прямые, радиально сходящиеся к центру полусферического забоя; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют сферические

поверхности.

 

 

БИЛЕТ 4