Закон распределения случайной величины – «наработка на отказ», порядок его построения и применения в практике работы УТТ.

Наработка - это работа изделия от начала эксплуатации до возникновения отказа (авто – км, спецтехника - моточасы).

Закон распределения случайной величины – это дифференциальная функция распределения плотности вероятности отказа f(t). f(t) – вероятность отказа за малую единицу времени при работе ДУА без замены.

Для процессов технической эксплуатации наиболее характерны следующие законы распределения:

1. нормальный закон

2. логарифмически нормальный закон

3. закон распределения Вейбула-Гнеденко

4. экспоненциальный закон

Кроме перечисленных, встречаются и другие законы распределения:

гамма-распределение

закон Релея

закон Пуассона

не получившие широкого применения в решении практических задач ТЭА.

Нормальный закон распределения формируется тогда, когда на протекание исследуемого процесса и его результат влияет большое число независимых факторов (слагаемых), каждое из которых в отдельности оказывает лишь незначительное действие по сравнению с суммарным влиянием всех остальных. В этом периоде эксплуатации постепенные отказы ещё не проявляются, и надёжность характеризуетсявнезапными отказами λ(t)=λ=const, λ=1/t.

 

Например, наработка до проведения ТО складывается из нескольких (десяти и более) сменных пробегов, отличающихся один от другого. Однако влияние одно сменного пробега на суммарную наработку незначительно и поэтому периодичность ТО подчиняется нормальному закону, для которого имеем: Плотность вероятности отказа это вероятность отказа за достаточно малый промежуток наработки ∆Х.

Зная плотность вероятности отказа можно рассчитать вероятность отказа за любой промежуток пробега, то есть можно спланировать количество запчастей, которое потребуется для каждой марки авто по каждому агрегату на предстоящий год. m_(x1-x2)≈ n*f(X)*∆X. Например n=75 термостатов, ∆X=4000 км f(42000)=0,2. m_{(40000-44000)} ≈0,2*4*75= 60 отказавших термостатов. Для нормального закона при расчетах часто пользуются понятием нормированной функции Ф(z), для которой принимается новая случайная величина так называемое нормируемое отклонение. Тогда: 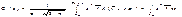Для нормированной функции составлены таблицы, облегчающие расчеты. Коэффициент вариации для этого закона не превышает 0,33.

ЛОГАРИФМИЧЕСКИ НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ. Если на протекание исследуемого процесса и его результат влияет сравнительно большое число случайных и взаимонезависимых факторов, интенсивность действия которых зависит от достигнутого случайной величиной состояния, то возникают условия для логарифмически нормального закона. Эта так называемая модель пропорционального эффекта рассматривает некоторую случайную величину, имеющую начальное состояние t₀ и конечное предельное состояние t_n. Изменение случайной величины происходит таким образом, что t_i=t_{i – 1} ε_i · h(t_{i – 1})

где ε_i – интенсивность изменения случайных величин;

h(t_{i – 1}) – функция реакции, показывающая характер изменения случайной величины.

Для такого закона имеем:

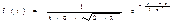
Таким образом, предельное состояние

а его логарифм lnt_n = lnt₀ + Σln(1  ε_i).

Согласно центральной предельной теореме lnt_n, имеем асимптотически нормальное распределение, как, сумма ряда случайных равновеликих и взаимонезависимых величин, а сама величина t_n распределена по логарифмически нормальному закону.

В технической эксплуатации этот закон встречается при описании процессов усталостных разрушений, коррозии, наработки до ослабления крепежных соединений и в ряде других случаев.

ЗАКОН РАСПРЕДЕЛЕНИЯ ВЕЙБУЛА-ГНЕДЕНКО Закон проявляется в модели так называемого «слабого звена». Если система состоит из группы независимых элементов, отказ каждого из которых приводит к отказу всей системы, то в такой модели рассматривается распределение времени (или пробега) достижения предельного состояния системы как распределение соответствующих минимальных значении t_i отдельных элементов: t_c = min (t₁, t₂… t_n). Функция распределения этой величины может быть выражена следующей зависимостью:

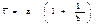
где, а и b – параметры распределения.

Примером использования распределения Вейбула-Гнеденко является распределение ресурса подшипника качения, который ограничивается одним из элементов шарик или ролик конкретный участок сепаратора и т.д. По аналогичной схеме наступает предельное состояние тепловых зазоров клапанного механизма. Некоторые изделия при анализе модели отказа могут быть рассмотрены как состоящие из нескольких элементов (участков): прокладки, уплотнения, шланги, трубопроводы, приводные ремни и т.д. Разрушение указанных изделий происходит в разных местах. Для этого закона в практических задачах ТЭА коэффициент вариации υ = 0,4 – 0,6.

ЭКСПОНЕНЦИАЛЬНЫЙ ЗАКОН является однопараметрическим, что облегчает расчеты и объясняет широкое распространение данного закона.

Вероятность безотказной работы при таком законе распределения ресурса до отказа имеет вид:

где λ – параметр потока отказов или интенсивность отказов, равный обратной величине средней наработке на отказ .

Плотность распределения тогда

При экспоненциальном законе распределения вероятность безотказной работы не зависит от того, сколько проработало изделие с начала эксплуатации, а определяется конкретной продолжительностью рассматриваемого периода или пробега. Таким образом, данный закон не учитывает постепенного изменения параметров технического состояния, например, в результате изнашивания, старения и т.д., а рассматривает так называемые нестареющие элементы и их отказы. Наибольшее распространение экспоненциальный закон получил при описании внезапных отказов, продолжительности ремонтных воздействий и в ряде других случаев.

Знание законов распределения случайных величин позволяет более точно планировать моменты и трудоемкость работ ТО и ремонта, определять необходимое количество запасных частей и решать другие технологические и организационные вопросы.

Нормальный закон распределения может применятся для определения количества автомобилей потребующих замены или ремонта ДУА на определенном этапе наработки.

Для определения закона распределения наработки до отказа необходимы статистические данные о неисправностях ДУА у исследуемых машин.

С этой целью на предприятии случайным образом из общего числа автомобилей одной марки, надежность которых изучается, отбирается группа машин, называемых выборкой. Выборка нужна для облегчения сбора информации о поведении ДУА, так как по разным причинам порой бывает трудно или даже невозможно, отследить за поведением изучаемого объекта на всех машинах.

Выборку представляет собой транспорт одной модели и марки, надежность которой изучается, причем, чем ближе друг к другу условия, в которых эксплуатируются автомобили, и чем ближе число машин в выборке к общему числу автомобилей данной модели, тем с большей уверенностью можно говорить о надежности всего парка данной марки по их поведению в выборке.

Далее фиксируются наработки, при которых будут происходить первые отказы ДУА на автомобилях выборки. Среди зафиксированных наработок находится минимальная t_min и максимальная t_max.

Определяется диапазон наработок внутри, которого имели место отказы: Д = t_max – t_min

Диапазон делится на интервалы, внутри которых сгруппировывается вся совокупность наработок. Длину интервала определяется по формуле:

где N – количество автомобилей в выборке.

Задаются левой t_лев и правой t_пр границами интервалов группирования, при этом t_лев должна быть меньше t_min, а t_пр больше t_max. Тогда число интервалов:

Интервалы нумеруются от одного до К и находится их середина. Подсчитывается количество изделий отказавших внутри каждого интервала (m). Это количество называется весом. Если какой-то отказ или группа отказов оказались на границе интервалов, то в эти интервалы добавляют по половине веса данных отказов.

Определённые данные для удобства расчета объединяются в таблицу, которая представляет собой результат наблюдения за выборкой. Выборка, когда все представленные на испытания объекты доработали до отказа, т. е. закончили испытания, называется полной. Если же испытания прекращены до того, как все изделия в выборке отказали, то выборка называется усеченной.

Далее рассчитывается накопленное число отказов к моменту t_i:

Определяется количество работоспособных объектов к моменту t_i: N(t_i) = N – m(t_i)

Находится вероятность безотказной работы. Вероятностью безотказной работы R(t_i) называется вероятность того, что в пределах заданной наработки не возникнет отказ изделий. Статически R(t_i) определяется отношением числа оставшихся работоспособными изделий N(t_i) к моменту наработки t_i, к общему числу изделий N в выборке.

Производится статистическая оценка плотности распределения наработки до отказа:

По рассчитанным в таблице результатам, строится графическое отображение закона распределения случайной величины.

Если заранее известно, что дифференциальная функция распределения будет иметь вид нормального закона распределения случайной величины и количество автомобилей в выборке значительно то, после фиксирования наработок, при которых будут происходить первые отказы ДУА автомобилей выборки (t_i), определяют среднюю наработку на отказ: и среднее квадратичное отклонение: Проводится оценка коэффициента вариации

Если рассчитанный υ_x больше 0,33, то полученный нормальный закон распределения будет обладать малой степенью достоверности. В таком случае принимается решение об использовании другого вида дифференциальной функции распределения.

Если υ_x ≤ 0,33. то закон распределения наработки до отказа определяется по формуле: