Электронный процессор Excel обладает мощной процедурой решения оптимизационных задач Поиск решения.
Загрузку надстройки Поиск решения можно выполнить следующим образом.
1. В Файл выбрать Параметры Excel
2. В окне Параметры выбрать Надстройки.
3. В поле Управление выбрать Надстройки Excel и нажать кнопку
Перейти.
4. В окне Надстройки включить Поиск решения.
5. На вкладке Данные становится доступной функция Поиск решения.
Для эффективного использования процедуры Поиск решения полезно соблюдать определенные правила подготовки информации.
Рассмотрим вначале линейные, квадратичные и нелинейные задачи общего вида, затем транспортные задачи ЛП.
Пусть нужно найти max целевой функции
z = x1 – 2x2
при условиях
-2 x1 + 3 x2 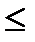 12,
12,
3 x1 – x2 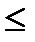 18,
18,
x1 + x2 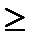 6,
6,
x1, x2 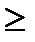 0.
0.
На листе Excel эти данные удобно расположить так, как показано на рис. 3.30.
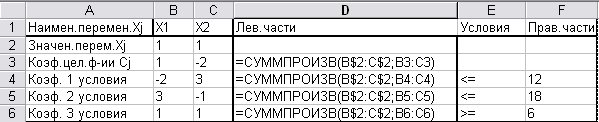
Рис.3.30 Решение линейной задачи общего вида (формулы)
Исходные значения переменных xj можно задать произвольно, например равными единице.
Для формирования целевой функции 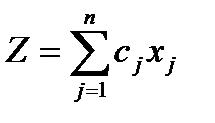 и всех левых частей ограничений
и всех левых частей ограничений 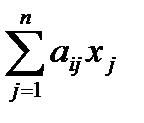 (i=1,…, m) используется функция СУММПРОИЗВ (fx →математические→ СУММПРОИЗВ), которая вызывается в строку коэффициентов целевой функции cj столбца левых частей (D3), а затем, после закрепления адреса строки «значения переменных хj», копируется в остальные строки этого столбца.
(i=1,…, m) используется функция СУММПРОИЗВ (fx →математические→ СУММПРОИЗВ), которая вызывается в строку коэффициентов целевой функции cj столбца левых частей (D3), а затем, после закрепления адреса строки «значения переменных хj», копируется в остальные строки этого столбца.
Для удобства ввода условий в процедуру Поиск решения их следует сгруппировать. Например, вначале записать все условия типа 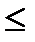 , затем
, затем 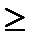 , затем =.
, затем =.
При такой подготовке в процедуру придется ввести не больше трех Групповых условий, что для больших задач существенно сокращает время ввода.
После подготовки исходных данных вызывается процедура Поиск решения (Данные → Анализ → Поиск решения).
В её диалоговом окне (рис. 3.31) устанавливается адрес ячейки, где находится целевая функция (D3), нужное значение экстремума (max), диапазон адресов значений переменных (B2:C2), диапазон адресов левых и правых частей условий типа 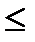 (Добавить →D4:D5
(Добавить →D4:D5 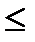 F4:F5 → Добавить), диапазон адресов левых и правых частей условий типа
F4:F5 → Добавить), диапазон адресов левых и правых частей условий типа 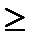 (Добавить – D6
(Добавить – D6 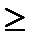 F6 – «OK»).
F6 – «OK»).
В следующем диалоговом окне Параметры устанавливаются флажки в позициях Линейная модель и Неотрицательные значения переменных. Вернувшись к первому диалоговому окну, нажимаем Выполнить.

Рис.3.31 Окно параметров поиска решения
В строке «Значения переменных хj» таблицы (рис. 3.32) получаем оптимальные значения неизвестных (х1=6, х2=0), а в ячейке целевой функции (D3) – соответствующее ее максимальное значение (Z=6).

Рис.3.32 Решение линейной задачи общего вида
Если решение получено, отмечается позиция Сохранить решение и интересующие пользователя типы отчетов (результаты, устойчивость, пределы).
Отчеты выводятся на отдельные листы Excel, которые вызывают из командной строки.
Если выводится сообщение, что решение не найдено, то либо задача поставлена некорректно (условия несовместимы или экстремум в бесконечности), либо поставленные в диалоговом окне Параметры ограничения по числу итераций, времени решения и точности слишком жесткие и их нужно ослабить (увеличить число итераций и время решения, уменьшить требования к точности).
Для решения задачи с нелинейной целевой функцией нужно в ячейку целевой функции ввести нужное выражение и в диалоговом окне Параметры снять флажок в позиции Линейная модель.
Например, чтобы решить рассмотренную выше задачу с целевой функцией
R =  → max
→ max
набираем эту функцию в ячейке (F3) и указываем ее в диалоговом окне Поиск решения.
В результате получим х1=6,35, х2=1,06, R=38,12 (рис. 3.33).
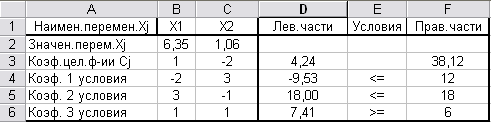
Рис.3.33 Результат решения линейной задачи общего вида
Для получения целочисленных решений достаточно в ограничения добавить диапазон изменяемых ячеек с условием целочисленные (цел).
Добавив условия целочисленности, в нашей задаче получим х1=6, х2=0, R=36 (в диалоговом окне Поиск решения → Добавить → В2:С2=целое).
Если просто округлить предыдущее решение до целых чисел х1=6, х2=1, то целевая функция R=34, что хуже целочисленного max.
Процедура Поиск решения успешно справляется не только с задачами квадратичного программирования, но и с задачами собственно нелинейного программирования.
Пусть нужно найти max целевой функции
R = 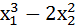
при условиях
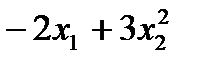
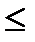 12,
12,

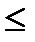 18,
18,
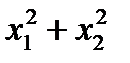
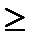 6,
6,
x1, x2 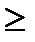 0.
0.
Исходные данные можно записать, например, в соответствии с
рис. 3.34.
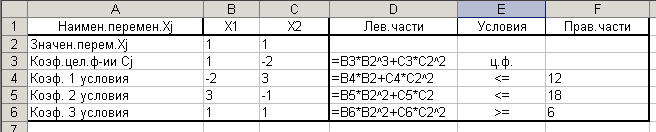
Рис.3.34 Решение нелинейной задачи
В результате решения получим
х1=2.470, х2=0.309, R=14.89
При решении транспортной задачи ЛП тоже важно удобно расположить исходные данные в таблице Excel.
Пусть нужно найти min затрат при перемещении грузов из трех пунктов отправления с запасами а1=8, а2=5, а3=7 в четыре пункта назначения с потребностями b1=4, b2=4, b3=2, b4=10.
Затраты на перемещение единицы груза по каждому маршруту соответствуют матрице:
Можно рекомендовать расположить исходные данные, как показано на рис. 3.35
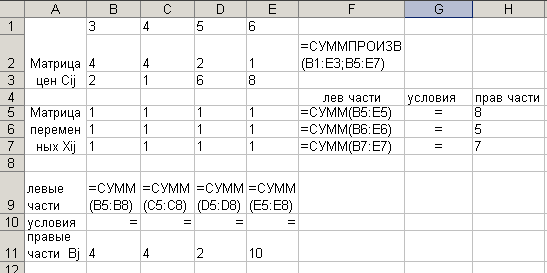
Рис.3.35 Решение транспортной задачи
Исходные значения всех неизвестных xij принимают произвольно, например, равными единицам.
Целевая функция формируется функцией СУММПРОИЗВ, в диалоговое окно которой первый массив сij и второй xij вводятся движениями курсора по главным диагоналям соответствующих матриц. Значения левых частей условий по запасам и по потребностям формируют функцией сумм (рис. 3.35).
Отметим, что условием существования решения является равенство суммы запасов и суммы потребностей:
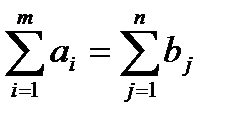 .
.
Если 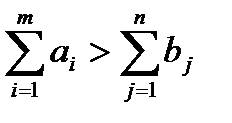 , для обеспечения баланса добавляется фиктивный пункт назначения с потребностями
, для обеспечения баланса добавляется фиктивный пункт назначения с потребностями 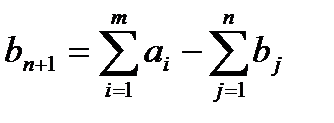 . Чтобы не менять величину целевой функции, затраты на перемещение грузов к фиктивному пункту принимаются равными нулю:
. Чтобы не менять величину целевой функции, затраты на перемещение грузов к фиктивному пункту принимаются равными нулю:
C i , n+1 = 0 (i=1, …, m).
Аналогично, если 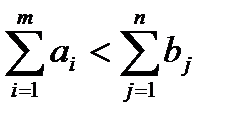 , добавляется фиктивный пункт отправления с запасами
, добавляется фиктивный пункт отправления с запасами  и затратами на перемещение
и затратами на перемещение
Cm+1, j = 0(j=1, …, n).
В диалоговом окне Поиск решения устанавливают адрес целевой функции, вид экстремума, вводят адреса массива неизвестных (курсор по диагонали матрицы хij).
В окно условий вводят (Добавить) диапазон адресов левых частей условий по запасам, знак равенства и соответствующий диапазон правых частей условий по запасам. Затем выполняют то же с условиями по потребностям (рис. 3.36).
В окне Параметры отмечают Линейная модель и Неотрицательные значения. Компоненты решения получают в матрице хij, а соответствующее значение целевой функции 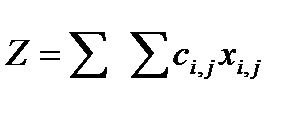 в ячейке F2 (рис. 3.37).
в ячейке F2 (рис. 3.37).
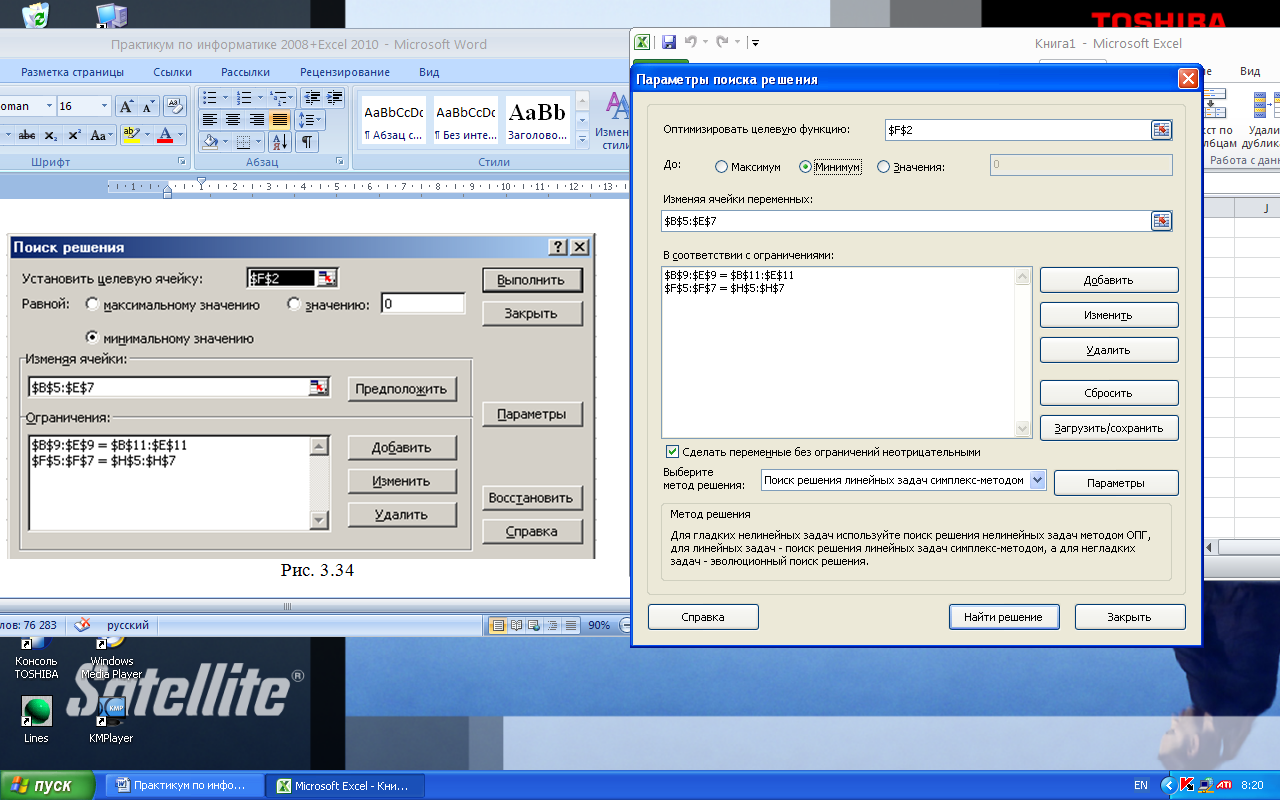
Рис.3.36 Параметры для решения транспортной задачи
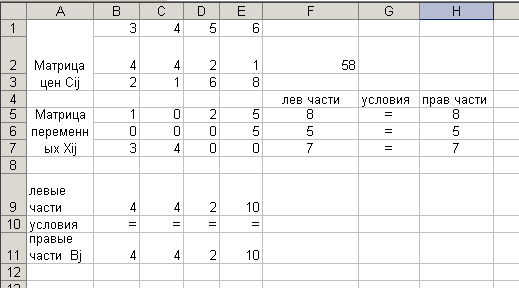
Рис.3.37 Результат решения транспортной задачи
При необходимости создаются отчеты по результатам, устойчивости, пределам.
Задание 9
Решите систему линейных уравнений из Задания 7 в § 8 с помощью процедуры Поиск решения. В качестве целевой функции возьмите выражение  . N – индивидуальный номер студента.
. N – индивидуальный номер студента.





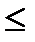 12,
12,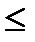 18,
18,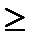 6,
6,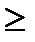 0.
0.
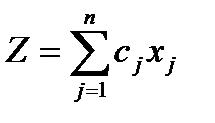 и всех левых частей ограничений
и всех левых частей ограничений 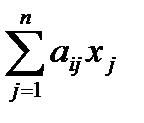 (i=1,…, m) используется функция СУММПРОИЗВ (fx →математические→ СУММПРОИЗВ), которая вызывается в строку коэффициентов целевой функции cj столбца левых частей (D3), а затем, после закрепления адреса строки «значения переменных хj», копируется в остальные строки этого столбца.
(i=1,…, m) используется функция СУММПРОИЗВ (fx →математические→ СУММПРОИЗВ), которая вызывается в строку коэффициентов целевой функции cj столбца левых частей (D3), а затем, после закрепления адреса строки «значения переменных хj», копируется в остальные строки этого столбца.

 → max
→ max
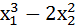
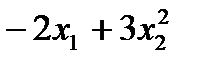

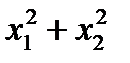


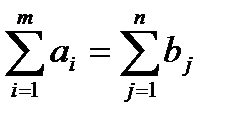 .
.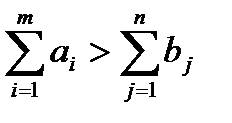 , для обеспечения баланса добавляется фиктивный пункт назначения с потребностями
, для обеспечения баланса добавляется фиктивный пункт назначения с потребностями 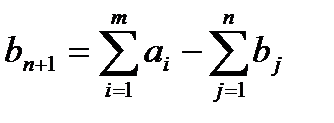 . Чтобы не менять величину целевой функции, затраты на перемещение грузов к фиктивному пункту принимаются равными нулю:
. Чтобы не менять величину целевой функции, затраты на перемещение грузов к фиктивному пункту принимаются равными нулю: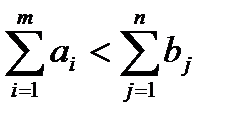 , добавляется фиктивный пункт отправления с запасами
, добавляется фиктивный пункт отправления с запасами  и затратами на перемещение
и затратами на перемещение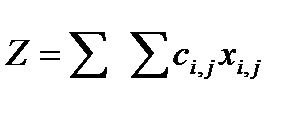 в ячейке F2 (рис. 3.37).
в ячейке F2 (рис. 3.37).

 . N – индивидуальный номер студента.
. N – индивидуальный номер студента.


