Теорема фон Неймана.
Пусть задана антагонистическая игра с платежной матрицей A (m, n) = (| aij |)
Определение. Смешанной стратегией игрока А называется дискретная случайная величина, принимающая значения 1,2,3,…m с определенной вероятностью;. смешанной стратегией игрока В называется дискретная случайная величина, принимающая значения 1,2,3,… n с определенной вероятностью.
P = (p1, p2 … pm), pi ≥ 0, ∑ pi = 1. Q = (q1, q2 … qn) (аналогично для Q).
Чистые стратегии игроков являются частными случаями смешанных, при этом
А1=(1,0,0,……0), А2=(0,1,0,……0) ….. Аm=(0,0,….0,1);
В1=(1,0,0,……0), В2=(0,1,0,……0) ….. Вn=(0,0,….0,1);
Тогда смешанные стратегии можно представить в виде
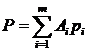 , Ai - базисные векторы
, Ai - базисные векторы
Проанализируем структуру множества смешанных стратегий. Пусть у игрока А есть две чистые стратегии.
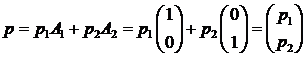 - это множество называется одномерным симплексом.
- это множество называется одномерным симплексом.
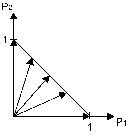
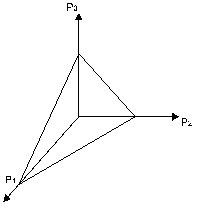
Для трех чистых стратегий имеем 2-мерный симплекс смешанных стратегий – треугольник с вершинами (1,0,0), (0,1,0), (0,0,1) (концы векторов P принадлежат треугольнику) и т.д.
Определение. Пара (P, Q) – образует исход игры (или игровую ситуацию). В которой выигрыш игрока A, равный aij, достигается с вероятностью piqj. H(P,Q) есть математическое ожидание выигрыша (средний выигрыш) при избранных стратегиях игроков 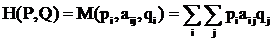 - средний выигрыш A (проигрыш B) при (P,Q). В матричном виде:
- средний выигрыш A (проигрыш B) при (P,Q). В матричном виде: 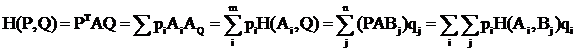
Пример. Пусть задана платежная матрица и стратегии игроков:
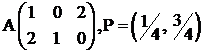 ,
, 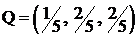 . Считаем векторы P, Q столбцами.
. Считаем векторы P, Q столбцами.
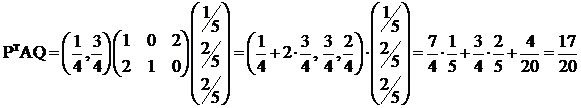
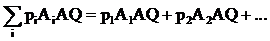
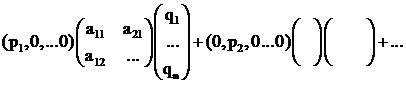
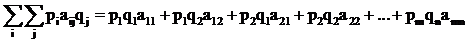
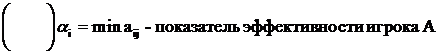
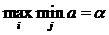 - нижняя цена игры.
- нижняя цена игры.
Определение. 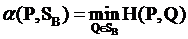 - показатель эффективности стратегии P игрока A относительно смешанной стратегии Q игрока B. (SB - множество смешанных стратегий игрока B.)
- показатель эффективности стратегии P игрока A относительно смешанной стратегии Q игрока B. (SB - множество смешанных стратегий игрока B.)
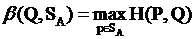 - показатель неэффективности стратегии Q игрока B.
- показатель неэффективности стратегии Q игрока B.
Теорема. Показатели α и β достижимы.Т.е.
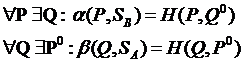
Доказательство:
Рассмотрим функцию α(P,SB). Для 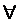 фиксированной стратегии P H(P,Q) - есть функция одной векторной переменной Q на ограниченном замкнутом контуре.
фиксированной стратегии P H(P,Q) - есть функция одной векторной переменной Q на ограниченном замкнутом контуре.
Ограниченность:
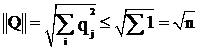 , ∑qi = 1, qi≥ 0
, ∑qi = 1, qi≥ 0
Замкнутость.
Вспомним, что множество называется замкнутым, если оно содержит все свои предельные точки
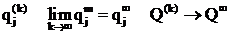 . Если каждый элемент сходящейся числовой последовательности неотрицателен, то и ее предел (очевидно) также неотрицателен, т.е.
. Если каждый элемент сходящейся числовой последовательности неотрицателен, то и ее предел (очевидно) также неотрицателен, т.е. 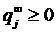 Далее:
Далее:  . Это доказывает, что симплекс – замкнутое множество.
. Это доказывает, что симплекс – замкнутое множество.
Теорема.
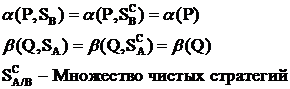
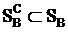 - множество чистых стратегий является подмножеством смешанных стратегий.
- множество чистых стратегий является подмножеством смешанных стратегий.
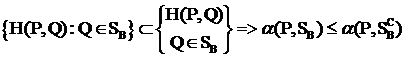
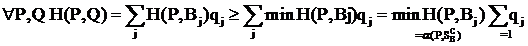
Верно для H(P, Q0) = α(P, SB)
Определение. Нижней ценой игры в смешанных стратегиях называется величина:
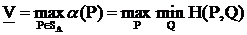
Верхней ценой игры в смешанных стратегиях называется величина:
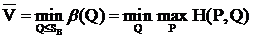
Теорема.
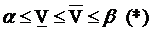 где α, β - цены игры в чистых стратегиях.
где α, β - цены игры в чистых стратегиях.
Доказательство:
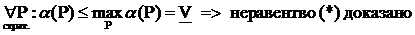
Докажем, что 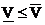 : Для произвольных стратегий P и Q имеем:
: Для произвольных стратегий P и Q имеем:
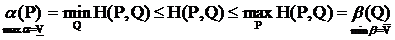
Определение. Если 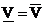 , то игра имеет цену в смешанных стратегиях => Максиминная и минимаксная стратегии тогда являются оптимальными.
, то игра имеет цену в смешанных стратегиях => Максиминная и минимаксная стратегии тогда являются оптимальными.
Теорема. (Основная теорема антагонистических игр.) Для любой матричной игры существует решение в смешанных стратегиях (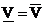 , минимаксные стратегии оптимальны).
, минимаксные стратегии оптимальны).
Без доказательства.
Тема 3. Лекция 9. Антагонистические игры.





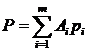 , Ai - базисные векторы
, Ai - базисные векторы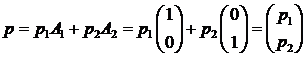 - это множество называется одномерным симплексом.
- это множество называется одномерным симплексом.

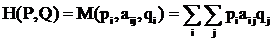 - средний выигрыш A (проигрыш B) при (P,Q). В матричном виде:
- средний выигрыш A (проигрыш B) при (P,Q). В матричном виде: 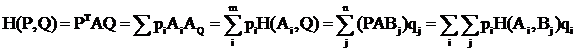
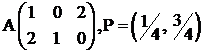 ,
, 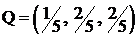 . Считаем векторы P, Q столбцами.
. Считаем векторы P, Q столбцами.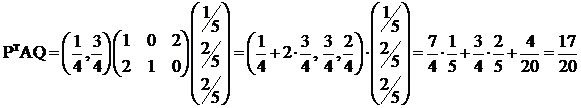
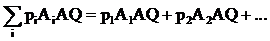
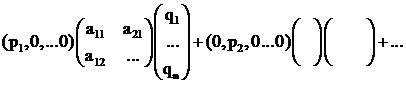
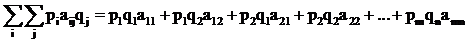
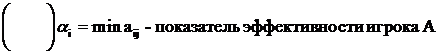
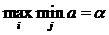 - нижняя цена игры.
- нижняя цена игры.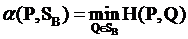 - показатель эффективности стратегии P игрока A относительно смешанной стратегии Q игрока B. (SB - множество смешанных стратегий игрока B.)
- показатель эффективности стратегии P игрока A относительно смешанной стратегии Q игрока B. (SB - множество смешанных стратегий игрока B.)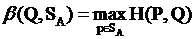 - показатель неэффективности стратегии Q игрока B.
- показатель неэффективности стратегии Q игрока B.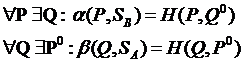
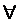 фиксированной стратегии P H(P,Q) - есть функция одной векторной переменной Q на ограниченном замкнутом контуре.
фиксированной стратегии P H(P,Q) - есть функция одной векторной переменной Q на ограниченном замкнутом контуре.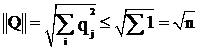 , ∑qi = 1, qi≥ 0
, ∑qi = 1, qi≥ 0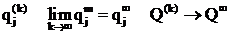 . Если каждый элемент сходящейся числовой последовательности неотрицателен, то и ее предел (очевидно) также неотрицателен, т.е.
. Если каждый элемент сходящейся числовой последовательности неотрицателен, то и ее предел (очевидно) также неотрицателен, т.е. 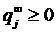 Далее:
Далее:  . Это доказывает, что симплекс – замкнутое множество.
. Это доказывает, что симплекс – замкнутое множество.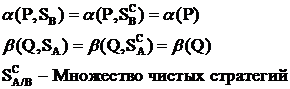
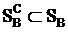 - множество чистых стратегий является подмножеством смешанных стратегий.
- множество чистых стратегий является подмножеством смешанных стратегий.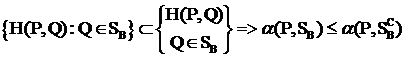
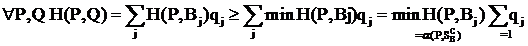
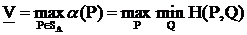
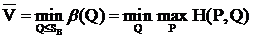
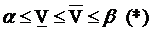 где α, β - цены игры в чистых стратегиях.
где α, β - цены игры в чистых стратегиях.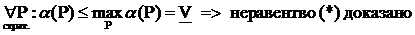
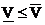 : Для произвольных стратегий P и Q имеем:
: Для произвольных стратегий P и Q имеем: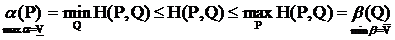
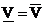 , то игра имеет цену в смешанных стратегиях => Максиминная и минимаксная стратегии тогда являются оптимальными.
, то игра имеет цену в смешанных стратегиях => Максиминная и минимаксная стратегии тогда являются оптимальными.


