Определение: Эффективным распределением супераддитивной игры (N, v) называется вектор х = (х1, x2,..., хn), такой, что (17) 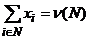
Определение: Дележом для игры (N, v) называется эффективное распределение, удовлетворяющее условию (18) 
Множество дележей игры (N, v) будем обозначать E (v).
Условие (17) ограничивает понятие дележа лишь случаем, когда игроки достигли достаточного взаимопонимания, чтобы образовать коалицию, состоящую из всех игроков.
Условие (18) называемое еще индивидуальной рациональностью (individual rationality), предлагает рассматривать только распределения полезности, дающие каждому игроку значения выигрыша не меньшие, чем он получил бы, действуя в одиночку. Это условие позволяет сразу ограничится рассмотрением только множества инивидуально рациональных распределений дохода между игроками.
Определение дележа приводит к понятию существенных игр.
Супераддитивная игра называется существенной, если (19)  .
.
В противном случае супераддитивная игра называется несущественной.
Несущественность игры означает нулевой эффект от кооперации. Действительно, выигрыш любой коалиции в несущественной игре равен просто сумме индивидуальных выигрышей ее
участников.
Множество дележей несущественной игры состоит из единственного элемента (20) 
Доказательство этого утверждения следует непосредственно из определений дележа и несущественной игры (см. (18)-(20)).
Обычно рассматриваются лишь существенные игры, так как вопрос о поиске решения среди дележей несущественной игры тривиален.
Пусть х и у — два дележа, и S— произвольная коалиция. Говорят, что х доминирует у по коалиции S (обозначается х >s у), если (21)  , (22)
, (22)  .
.
Если существует коалиция S, такая, что x>s у, говорят, что х доминирует у (обозн. x> у).
Условие (21) означает, что дележ х лучше дележа у для членов коалиции S, а условие (22) отражает реализуемость дележа х коалицией S - если оно выполнено, то коалиция действительно может предложить своим участникам выигрыши  .
.
Определение: Игры п лиц с характеристическими функциями и и v называются изоморфными, если существует функция f, взаимно однозначно отображающая множество дележей игры и на множество дележей игры v таким образом, что для любой пары дележей х и у игры и и произвольной коалиции S из доминирования дележа л дележом у следует доминирование образа f(x) образом f(y). Иначе говоря, х>sy у  f{x) >s f(y), где
f{x) >s f(y), где  - дележи игры v.
- дележи игры v.
При анализе свойств игры с помощью отношения доминирования полезно значь, у каких игр множества дележей имеют одинаковую структуру доминирования, то есть какие игры являются изоморфными.
Определение: Игры п лиц и и v называются S-эквивалентными, если существует положительное число rи п таких вещественных чисел  что для любой коалиции
что для любой коалиции 
(23)  .
.
Теорема. Если и и v являются S-эквивалентными, то они изоморфны.
Определение: Игра v называется игрой в (0, 1)- редуцированной форме, если
 .
.
Теорема|. Любая существенная игра S-эквивалентна одной и только одной игре в (0, 1)-редуцированной форме.
Таким образом, определение вводит классы игр, изоморфных относительно операции доминирования, теорема дает удобный способ проверки изоморфности игр, а теорема утверждает, что анализ игр с помощью отношения доминирования можно ограничить анализом игр в (0, 1)-редуцированной форме.
Понятия дележа и доминирования дележей играют немаловажную роль в формулировках концепций решения, изложение которых представлено ниже.
5. Концепции решения кооперативных игр
В теории кооперативных игр, также как и вообще в теории игр, не существует единой концепции решения. Это связано с тем, что в начальной стадии развития теории были разработаны достаточно простые модели игр, которые легко поддавались анализу, и, соответственно, простые концепции решений, такие, как С-ядро и НМ-решения (см. ниже). По мере развития теории встал вопрос о практической применимости полученных результатов. Для того чтобы приблизить теорию к примерам игр, встречающихся в жизни, были разработаны более сложные модели, например, игры с нетрансферабельной полезностью, игры «в разбиениях» и др. Параллельно появлялись как обобщения понятий решения на эти более сложные модели, так и новые концепции решений — см. ниже.
Некоторые концепции решения пришли в теорию игр из теорий общественного благосостояния и кооперативного выбора. Темой исследования этих теорий является задача выбора коллективных решений в обществе. Понятно, что коллективный выбор должен быть (или желательно, чтобы был) единственным. Для сужения круга возможных решений эти теории пользуются аксиоматическими предположениями о стратегии принятия коллективных решений. В этих аксиомах широко используется понятие «справедливого» распределения благ (то есть распределения выигрышей, полезности и т.д.).
С понятием справедливости в условиях принятия решения обществом связана отдельная проблематика. Аксиоматический подход предполагает, что при исследовании ситуации выбора, для того, чтобы обосновать выбор общества, исследователь делает предположения, более или менее очевидные, о моральных установках данного общества, и, тем самым, определяет, что в данном обществе понимается под справедливостью. Парадокс состоит в том, что многие достаточно очевидные и соответствующие здравому смыслу по отдельности предположения оказываются противоречащими друг другу. На сегодняшний момент в науке не существует единого мнения о том, что понимать под справедливостью. Двумя основными концепциями справедливого распределения благ являются эгалитаризм и утилитаризм. Эгалитаризм утверждает, что при распределении благ в первую очередь следует обращать внимание на полезность наиболее «обделенных» членов общества. Утилитаризм же считает справедливым «эффективное» распределение, приводящее к наибольшей сумме полезностей членов общества. Применение этих концепций к теории кооперативных игр приводит к понятиям N-ядра и вектора Щепли соответственно.
Все концепции решения кооперативных игр, определяющие в качестве решения единственное распределение полезности между игроками, называются значениями игры.
6. С-ядро
Если игроки пришли к такому дележу х выигрыша максимальной коалиции, что не существует дележа, доминирующего дележ x. то дележ x устойчив в том смысле, что никакой коалиции S не выгодно отделяться от коалиции N и делить между членами этой коалиции выигрыш v(S).
Теорема. Для того чтобы дележ х принадлежал С-ядру, необходимо и достаточно выполнения для всех 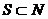 неравенств (24)
неравенств (24)  .
.
Доказательство очевидно.
Эта теорема дает удобный способ нахождения С-ядра путем решения системы неравенств. Решением этой линейной системы является выпуклый многогранник в пространстве  . Можно найти его крайние точки и описать любой дележ из ядра, как взвешенную линейную комбинацию крайних точек.
. Можно найти его крайние точки и описать любой дележ из ядра, как взвешенную линейную комбинацию крайних точек.
Итак, С-ядро существует не для всех игр. Мало того, даже условие супераддитивности является лишь необходимым, но не достаточным условием существования непустого ядра. Например, все игры с постоянной суммой имеют пустое С-ядро.
Необходимым и достаточным условием существования непустого ядра является свойство сбалансированности игры.
Определение: Максимальной коалицией называется коалиция, состоящая из всех игроков.
Определение: Собственной коалицией называется коалиция, отличная от максимальной коалиции.
Определение: Для данного множества игроков N сбалансированным покрытием называется такое отображение  из
из 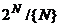 в [0,1], что
в [0,1], что  для всех игроков I,
для всех игроков I,
причем суммирование в (27) ведется по всем собственным коалициям, содержащим игрока i.
Теорема. С-ядро игры (N, v) не пусто тогда и только тогда, когда для любого сбалансированного покрытия  выполнено неравенство (27)
выполнено неравенство (27)  .
.
Если для игры выполнено условие (27), то игра называется сбалансированной.
Например, для супераддитивной игры трех лиц непустоту С-ядра гарантирует следующее дополнительное (к условиям супераддитивности) условие v ({l,2}) + v ({l,3}) + v ({2,3})<2 v (V). Для игры четырех лиц условия сбалансированности задаются уже семью дополнительными неравенствами, и т.д.





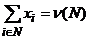

 .
.
 , (22)
, (22)  .
. .
. f{x) >s f(y), где
f{x) >s f(y), где  - дележи игры v.
- дележи игры v. что для любой коалиции
что для любой коалиции 
 .
. .
.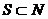 неравенств (24)
неравенств (24)  .
. . Можно найти его крайние точки и описать любой дележ из ядра, как взвешенную линейную комбинацию крайних точек.
. Можно найти его крайние точки и описать любой дележ из ядра, как взвешенную линейную комбинацию крайних точек. из
из 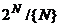 в [0,1], что
в [0,1], что  для всех игроков I,
для всех игроков I, .
.


