Вычисление равновесий Нэша
Чтобы для конкретной игры вычислить равновесие Нэша в чистых стратегиях, необходимо проверить наличие собственного значения оператора R для собственного числа 1. Оператор R - отображение произвольной игровой ситуации на совокупность лучших ответов игроков на задаваемую для них этой ситуацией обстановку. Таким образом, для бесконечных игр, задача сводится к нахождению вида этого оператора и решения уравнения
x* = R(x*) (1)
Пример. Вычисление равновесий Нэша для игры «Фермеры на общем поле».
Целевые функции игроков в этой игре Ki = хi (120 – х1 - х2). Функции выигрыша вогнуты по стратегиям игроков, поэтому в этой игре существует равновесие Нэша в чистых стратегиях.
Наилучший ответ игрока при фиксированном поведении противника вычисляется в результате нахождения максимума функции выигрыша по стратегии этого игрока, то есть xi*=Ri(x-i) = arg max Ki (xi,x-i). Частная производная в этой точке равна нулю, то есть 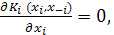 значит x1 =60–
значит x1 =60–  , i=1,2.
, i=1,2.
Получили систему уравнений

решением которой является пара стратегий x1 = х2 = 40, приводящих к выигрышам K1= К2 = 1600.
Заметим, что при условии безусловного сотрудничества игроков, то есть в случае объединения их выигрышей и выбора стратегий из условия максимизации нового критерия К = К1(х1, х2) + К2(х1, х2), стратегии игроков были бы х1 = х2 = 30.
При этом K = 3600, то есть при распределении выигрыша поровну на долю каждого из игроков достается по 1800 единиц, что больше, чем при конкуренции. Эта оптимальная по Парето ситуация, не является, однако, равновесной, так как неустойчива по односторонним отклонениям игроков от оптимальной по Парето стратегии.
Система (1) может давать несколько решений, и все они будут равновесиями Нэша.
Кроме того, уравнения системы (1) могут оказаться зависимыми. Это значит, что равновесий Нэша в этой игре бесконечное множество. Например, для игры двух лиц с функциями выигрыша Кi = l(x1 +x2- c)-xi, где l(x):=  множество равновесных ситуаций описывается равенством x1 + х2 = с. Такая ситуация характерна в основном для игр с разрывной функцией выигрыша.
множество равновесных ситуаций описывается равенством x1 + х2 = с. Такая ситуация характерна в основном для игр с разрывной функцией выигрыша.
Пример. «Нахождение равновесий Нэша в смешанных стратегиях в игре «Семейный спор».
Пусть матрица выигрышей имеет вид 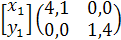
Смешанная стратегия первого игрока определяется одним числом р – вероятностью выбора им первой стратегии, смешанная стратегия второго, соответственно, числом q. Вычисляем:
K1(x1,qx2 +(1 - q)y2) = 4q, K1(x2,qx2 + (1 - q)y2) = 1 – q.
Таким образом, при q < 0,25, наилучшим ответом первого игрока является стратегия у1, при q>0,25 - стратегия х1. При q = 0,25 обе стратегии равнозначны с точки зрения ожидаемого выигрыша. То есть наилучший ответ первого игрока:
p*(q) = 
Аналогично, наилучший ответ второго игрока:
q*(p) = 
Существуют принципы оптимальности, которые могут быть обоснованы только динамическим сценарием, в котором принимаемые стратегические решения зависят от предыдущих партий игры или хотя бы от начальной позиции. К числу таких принципов оптимальности относится один из наиболее распространённых – равновесие по Нэшу.
Для данной игры в нормальной форме предположим, сто игроки ведут себя так, как будто они не знают о своей стратегической взаимозависимости: когда игрок i рассматривает переключение со стратегии xi на стратегию yi, он не учитывает реакции остальных игроков на свой ход, т.е. ожидает, что остальные не изменят своей стратегии в ответ на его изменение. Это предположение правдоподобно, если игроков так много, что воздействие, производимое на общий исход одним отклонением, незначительно (см. пример 8).
Ещё одна возможная интерпретация предполагает полное знание игроком i функций выигрыша uj при  . Игрок может добывать информацию о функциях uj, наблюдая реакции игроков из
. Игрок может добывать информацию о функциях uj, наблюдая реакции игроков из  на используемые им стратегии, выгодные в том положении, что никакой реакции остальных не последует.
на используемые им стратегии, выгодные в том положении, что никакой реакции остальных не последует.
Определение1. пусть дана игра в нормальной форме (9.1). Исход 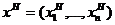 есть равновесие по Нэшу (NE-исход) игры Г, если
есть равновесие по Нэшу (NE-исход) игры Г, если

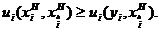
Обозначим через NE(Г) множество равновесий по Нэшу в игре Г.
Пример: двоичный выбор с взаимным влиянием.
Пусть имеется много идентичных игроков. Каждый из них должен выбрать одну из двух стратегий: 0 (использовать собственный автомобиль) или 1 (ездить на автобусе).
Если s, 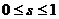 , - доля игроков, использующих стратегию 1, то числа
, - доля игроков, использующих стратегию 1, то числа  и
и  обозначают соответственно выигрыши любого игрока, использующего стратегию 1 и стратегию 0 соответственно. Тогда получаем следующую игру в нормальной форме:
обозначают соответственно выигрыши любого игрока, использующего стратегию 1 и стратегию 0 соответственно. Тогда получаем следующую игру в нормальной форме:
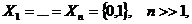
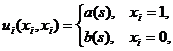
 .
.
Пусть функции  ,
,  такие, как на рис.????.
такие, как на рис.????.
Это означает, что если доля игроков, использующих общественный транспорт, больше  , то уличное движение настолько свободное, что водитель автомобиля счастливее, чем пассажиры автобуса. Если же доля автомобилистов больше, чем
, то уличное движение настолько свободное, что водитель автомобиля счастливее, чем пассажиры автобуса. Если же доля автомобилистов больше, чем  , то движение настолько интенсивное, что сравнение теперь в пользу пассажиров автобусов.
, то движение настолько интенсивное, что сравнение теперь в пользу пассажиров автобусов.
В этой игре равновесиями по Нэшу являются исходы  , для которых выполнено условие
, для которых выполнено условие
 ,
,  ,
,  ,
,
означающее, что для каждого отдельно взятого игрока обе допустимые стратегии равноценны.
Положим, например,  ,
,  ,
, 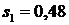 .Тогда получаем
.Тогда получаем 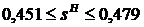 ,
,  . Отсюда следует, что равновесными по Нэшу являются все такие исходы
. Отсюда следует, что равновесными по Нэшу являются все такие исходы 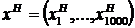 , для которых от 451 до 479 компонент равны (т.е. соответствующие игроки ездят автобусом).
, для которых от 451 до 479 компонент равны (т.е. соответствующие игроки ездят автобусом).





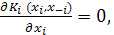 значит x1 =60–
значит x1 =60–  , i=1,2.
, i=1,2.
 множество равновесных ситуаций описывается равенством x1 + х2 = с. Такая ситуация характерна в основном для игр с разрывной функцией выигрыша.
множество равновесных ситуаций описывается равенством x1 + х2 = с. Такая ситуация характерна в основном для игр с разрывной функцией выигрыша.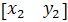
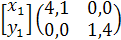


 . Игрок может добывать информацию о функциях uj, наблюдая реакции игроков из
. Игрок может добывать информацию о функциях uj, наблюдая реакции игроков из  на используемые им стратегии, выгодные в том положении, что никакой реакции остальных не последует.
на используемые им стратегии, выгодные в том положении, что никакой реакции остальных не последует.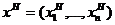 есть равновесие по Нэшу (NE-исход) игры Г, если
есть равновесие по Нэшу (NE-исход) игры Г, если
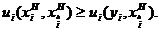
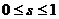 , - доля игроков, использующих стратегию 1, то числа
, - доля игроков, использующих стратегию 1, то числа  и
и  обозначают соответственно выигрыши любого игрока, использующего стратегию 1 и стратегию 0 соответственно. Тогда получаем следующую игру в нормальной форме:
обозначают соответственно выигрыши любого игрока, использующего стратегию 1 и стратегию 0 соответственно. Тогда получаем следующую игру в нормальной форме: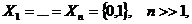
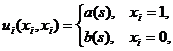
 .
. , то уличное движение настолько свободное, что водитель автомобиля счастливее, чем пассажиры автобуса. Если же доля автомобилистов больше, чем
, то уличное движение настолько свободное, что водитель автомобиля счастливее, чем пассажиры автобуса. Если же доля автомобилистов больше, чем  , то движение настолько интенсивное, что сравнение теперь в пользу пассажиров автобусов.
, то движение настолько интенсивное, что сравнение теперь в пользу пассажиров автобусов. , для которых выполнено условие
, для которых выполнено условие ,
,  ,
,  ,
, ,
,  ,
, 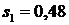 .Тогда получаем
.Тогда получаем 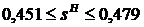 ,
,  . Отсюда следует, что равновесными по Нэшу являются все такие исходы
. Отсюда следует, что равновесными по Нэшу являются все такие исходы 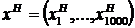 , для которых от 451 до 479 компонент равны (т.е. соответствующие игроки ездят автобусом).
, для которых от 451 до 479 компонент равны (т.е. соответствующие игроки ездят автобусом).


