Отыскание решения игр без седловой точки, особенно при достаточно больших размерах платежной матрицы, оказывается довольно сложной задачей. В некоторых случаях эту задачу можно упростить с помощью редуцирования игр, т.е. сведения данной игры со сложной матрицей к игре с более простой матрицей. В этом параграфе мы рассмотрим один из способов редуцирования игр, основанный на принципе доминирования, который позволяет в некоторых случаях игру с матрицей большего размера свести к игре с матрицей меньшего размера.
Пусть имеем игру с матрицей A размера m*n.
| Bj
Ai
| B1
| B2
| …
| Bn
|
| A1
| a11
| a12
| …
| a1n
|
| A2
| a21
| a22
| …
| a2n
|
| …
| …
| …
| …
| …
|
| Am
| am1
| am2
| …
| amn
|
Каждой смешанной (в частности, чистой) стратегии Р=(р1, р2,…, рm)игрока A поставим в соответствие строку
(H(P, B1), H(P, B2),…, H(P, Bn)) (2.11.1)
(размера 1хn), элементами которой являются выигрыши H(P, Bj), j=1,2,…,n, игрока А в ситуациях (P, Bj), j=1,2,…,n.
В силу формулы (2.8.8), строку (2.11.1) можно представить так:
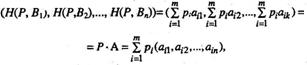 (2.11.2.)
(2.11.2.)
откуда видно, что она является выпуклой комбинацией строк матрицы А (выпуклой потому, что коэффициенты р1, р2,…, рm неотрицательны и в сумме дают единицу).
Обратно, каждой выпуклой комбинации (2.11.2) строк матрицы А с коэффициентами р1, р2,…, рm поставим в соответствие смешанную стратегию Р=(р1, р2,…, рm)игрока А.
Таким образом, между смешанными (в том числе и чистыми) стратегиями
Р=(р1, р2,…, рm)игрока A и выпуклыми комбинациями

строк (а i1, а i2,…, а in), i=l,,.., m, матрицы А устанавливается взаимно-однозначное соответствие
 (2.11.3.)
(2.11.3.)
Из (2.11.1) или (2.11.3) ясно, что каждой чистой стратегии Ak, k=l, 2,...,m, игрока А ставится во взаимно-однозначное соответствие k-я строка (а k1, а k2,…, а kn), матрицы А.
Если для двух выпуклых комбинаций строк матрицы А
 (2.11.4.)
(2.11.4.)
и
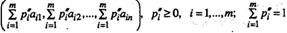 (2.11.5.)
(2.11.5.)
выполняются неравенства:
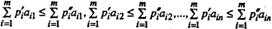 (2.11.6.)
(2.11.6.)
то говорят, что строка (2.11.5) доминирует строку (2.11.4), а строка (2.11.4) доминируется строкой (2.11.5). Таким образом, строка (2.11.5) — доминирующая строку (2.11.4), а строка (2.11.4) — доминируемая строкой (2. 11. 5).
Если каждое из неравенств (2.11.6) является равенством, то строки (2.11.4) и (2.11.5) называют дублирующими друг друга. Каждая из двух дублирующих строк является одновременно и доминируемой, и доминирующей другую.
Если каждое из неравенств (2.11.6) является строгим, то говорят, что строка (2.11.5) строго доминирует строку (2.11.4), а строка (2.11.4) строго доминируется строкой (2.11.5), или строка (2.11.5) является строго доминирующей строку (2.11.4), а строка (2.11.4) является строго доминируемой строкой (2.11.5).
Аналогичная терминология используется и для соответствующих стратегий игрока А. А именно, если строка (2.11.5) доминирует, соответственно дублирует, соответственно строго доминирует строку (2.11.4), то говорят, что стратегия Р" = (р1", р2",…, рn") доминирует, соответственно дублирует, соответственно строго доминирует стратегию Р' = (p1', p2',…, pn').
Так как элементами строк, соответствующих по (2.11.3) смешанным стратегиям, являются выигрыши игрока А (см. (2.11.1)), то из данных определений понятно, что для игрока А дублирующие стратегии равнопредпочтительны, а доминируемая не дублирующая стратегия заведомо для него невыгодна.
Аналогично, каждой смешанной (в частности, чистой) стратегии Q=(q1, q2,…, qn)игрока Впоставим в соответствие столбец
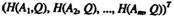 (2.11.7.)
(2.11.7.)
(размера mx1) его проигрышей H(Ai, Q), i=1,..., m,в ситуациях (Ai, Q), i=1,..., m. Используяформулы (2.8.7), столбец (2.11.7) можно представить следующим образом:
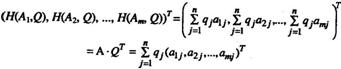 (2.11.8.)
(2.11.8.)
Отсюда видно, что столбец (2.11.7) является выпуклой комбинацией столбцов  , матрицы A с коэффициентами q1, q2,…, qn.
, матрицы A с коэффициентами q1, q2,…, qn.
Обратно, каждой выпуклой комбинации (2.11.8) столбцов матрицы А с коэффициентами:

Поставим в соответствие смешанную стратегию Q=(q1, q2,…, qn)игрока В.
Таким образом, между смешанными и чистыми стратегиями Q=(q1, q2,…, qn)? Sbигрока В и выпуклыми комбинациями
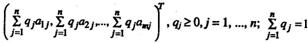
столбцов  , матрицы А устанавливается взаимно-однозначное соответствие
, матрицы А устанавливается взаимно-однозначное соответствие
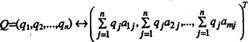 (2.11.9.)
(2.11.9.)
По которому, в частности, каждой чистой стратегии Bl, l=1,…,n, игрока В ставится во взаимно-однозначное соответствие l-й столбец 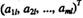 матрицы А (см. также(2.11.7.)).
матрицы А (см. также(2.11.7.)).
Если для двух выпуклых комбинаций столбцов матрицы А
 (2.11.10)
(2.11.10)
и
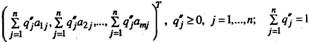 (2.11.11.)
(2.11.11.)
справедливы неравенства
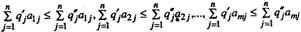 (2.11.12.)
(2.11.12.)
то говорят, что столбец (2.11.10) (стратегия Q' = (q1', q2',…, qn')) доминирует столбец (2.11.11) (стратегию Q"= (q1", q2",..., qn")), а столбец (2.11.11) (стратегия Q") доминируется столбцом (2.11.10) (стратегией Q').
В случае, когда каждое неравенство (2.11.12) является равенством, столбцы (2.11.10) и (2.11.11) (стратегии Q' и Q") называются дублирующими.
Если каждое неравенство (2.11.12) является строгим, то столбец (2.11.10) (стратегия Q')называется строго-доминирующим (строго доминирующей) столбец (2.11.11) (стратегию Q"), а столбец (2.11.11) (стратегия Q") — строго доминируемым (строго доминируемой) столбцом (2.11.10) (стратегией (Q').
Поскольку элементами столбцов, соответствующих по (2.11.9) смешанным стратегиям игрока В, являются его проигрыши, то для него дублирующие стратегии равнопредпочтительны, а доминируемая не дублирующая стратегия заведомо невыгодна.
Таким образом, по данным определениям и для игрока А,и для игрока В предпочтительными оказываются доминирующие стратегии.
Теорема 2.11.1 Справедливы следующие предложения:
1) Если k-я строка, k?۟ {l,...,m}, матрицы Аигры, доминируется некоторой выпуклой комбинацией остальных ее строк, то существует оптимальная смешанная
стратегия  игрока А, в которой k-я чистая стратегия Akвыбирается
игрока А, в которой k-я чистая стратегия Akвыбирается
им с нулевой вероятностью, т.е. 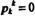 .
.
2) Если k-я строка, k?۟ {l,...,m}, матрицы Аигры, строго доминируется некоторой выпуклой комбинацией остальных ее строк, то в любой оптимальной смешанной стратегии Р° = (p1°,..., pm°) игрока Ачистая k-я стратегия Akвыбирается
им с нулевой вероятностью, т.е. рk° = 0.
3) Если l-й столбец, l?{1,...,n), матрицы А игры, доминируется некоторой выпуклой комбинацией остальных ее столбцов, то существует оптимальная смешанная стратегия 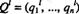 игрока В,в которой l-ячистая стратегия Вl выбирается им с нулевой вероятностью, т.е. ql=0.
игрока В,в которой l-ячистая стратегия Вl выбирается им с нулевой вероятностью, т.е. ql=0.
4) Если 1-йстолбец, l?{1,...,n}, матрицы A игры, строго доминируется некоторой выпуклой комбинацией остальных ее столбцов, то в любой оптимальной
смешанной стратегии Q°= (q1°,..., qn°)игрока В, чистая 1-ястратегия Вlвыбирается им с нулевой вероятностью, т.е. q1°=0
Доказательство. Докажем утверждение 1).
Пусть k-я строка матрицы А доминируется некоторой выпуклой комбинацией остальных ее строк. В этом случае мы можем считать, что k-я строка доминируется выпуклой комбинацией всех т строк матрицы А, но коэффициент при k-й строке в этой комбинации равен нулю. Таким образом, найдутся коэффициенты
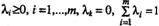 (2.11.13.)
(2.11.13.)
Такие, что строка (ak1,…, akn) доминируется выпуклой комбинацией 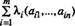 , что по определению доминирования строк означает (см.(2.11.6.)) выполнение неравенств
, что по определению доминирования строк означает (см.(2.11.6.)) выполнение неравенств
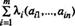 (2.11.14.).
(2.11.14.).
Пусть P°= (p1°,..., pm°) некоторая оптимальная смешанная стратегия игрока А, существование которой гарантировано основной теоремой матричных игр фон Неймана (см. теорему 2.9.1.). Рассмотрим смешанную стратегию  игрока А с координатами
игрока А с координатами
 (2.11.15.)
(2.11.15.)
Нетрудно убедиться в том, что числа 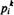 - неотрицательны и в сумме дают единицу. В самом деле, поскольку
- неотрицательны и в сумме дают единицу. В самом деле, поскольку 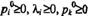 , то
, то 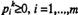 , а так как גk=0,
, а так как גk=0, 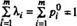 , то
, то

Пусть V – цена игры. Тогда, в силу оптимальности стратегии P°, по необходимой части утверждения 1) теоремы 2.10.2, H(P°, Bj) ≥ V, j = 1,…,n.
Следовательно, в силу (2.8.8.), (2.11.15.), (2.11.14.),


Полученные неравенства  ≥ V, j = 1,…,n, означают по достаточной части утверждения 1)теоремы 2.10.2, что
≥ V, j = 1,…,n, означают по достаточной части утверждения 1)теоремы 2.10.2, что 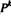 является оптимальной стратегией, причем
является оптимальной стратегией, причем  =0.
=0.
Таким образом, утверждение 1) доказано.
Заметим, что при доказательстве утверждения 1), на самом деле доказано несколько большее, чем «чистое» существование требуемой в утверждении 1) оптимальной стратегии, а именно, указан способ ее конструирования (см. (2.11.15)).
Докажем утверждение 2). Пусть k-я строка матрицы Астрого доминируется некоторой выпуклой комбинацией остальных ее строк, т.е. найдутся коэффициенты, обладающие свойствами (2.11.13), такие, что k-я строка (ak1,…, akn) строго доминируется выпуклой комбинацией  , или, по определению строгого доминирования строк,
, или, по определению строгого доминирования строк, 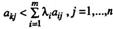 (2.11.16.).
(2.11.16.).
Пусть Q°= (q1°,..., qn°) - произвольная оптимальная стратегия игрока В (существование которой обеспечено основной теоремой теории игр фон Неймана). Умножим неравенство (2.11.16) на qj°получим:
 (2.11.17.)
(2.11.17.)
Неравенство (2.11.17) превращается в равенство (обе части которого нули) для тех номеров j, для которых q1° = 0, и — в строгое неравенство для остальных номеров j. Поскольку q1° +…+ qn° = 1, то не все qj°равны нулю и потому хотя бы одно из неравенств (2.11.17) будет строгим. Следовательно, просуммировав неравенства (2.11.17), получим строгое неравенство
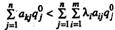 (2.11.18.)
(2.11.18.)
Но, по (2.8.5),
 (2.11.19.)
(2.11.19.)
А по (2.8.2.)
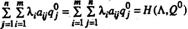 (2.11.20.)
(2.11.20.)
Где ג = (ג1,…,גm) является, в силу свойств (2.11.13.), некоторой смешанной стратегией игрока А.
Из (2.11.19), (2.11.18) и (2.11.20):
 (2.11.21)
(2.11.21)
По необходимой части утверждения 2) теоремы 2.10.1, 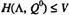 и потому из (2.11.21):
и потому из (2.11.21):
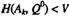 (2.11.22)
(2.11.22)
Пусть P°— произвольная оптимальная стратегия игрока А. Нам надо показать, что рk° = 0. Допустим противное: рk° > 0. Тогда чистая стратегия Ak игрока А является активной и по теореме 10.6 об активных стратегиях (см.(2.10.21)) должно выполняться равенство H(Ak, Q°) = V, которое противоречит неравенству (2.11.22). Полученное противоречие завершает доказательство утверждения 2).
Утверждения 3) и 4) доказываются аналогично соответственно утверждениям 1) и 2).
Отметим, что из утверждения 1) теоремы 2.11.1 следует, что если k-я строка матрицы игры нестрого доминируется некоторой выпуклой комбинацией остальных ее строк, то k-ю строку можно удалить, уменьшив тем самым размер матрицы. Вместе с тем могут существовать оптимальные стратегии игрока А, включающие в себя чистую стратегию Ak с положительной вероятностью. Таким образом, при нестрогой доминируемости k-й строки чистая стратегия Ak игрока А не может считаться для него абсолютно невыгодной.
Утверждение 2) теоремы 2.11.1 означает, что если k-я строка матрицы игры строго доминируется некоторой выпуклой комбинацией остальных ее строк, то ее нужно удалить, поскольку чистая стратегия Ak априори невыгодна игроку А.
Аналогичные замечания относятся к доминируемым столбцам матрицы игры в утверждениях 3) и 4).
Следствие 2.11.1.
1) Если k-я строка матрицы игры доминируется (строго доминируется) некоторой другой строкой, то существует (любая) оптимальная смешанная стратегия игрока А, в которую чистая стратегия Ak входит с нулевой вероятностью.
2) Если l-й столбец матрицы игры доминируется (строго доминируется) некоторым другим столбцом, то существует (любая) оптимальная смешанная стратегия игрока В, в которую чистая стратегия Bl входит с нулевой вероятностью.
Доказательство. 1) Пусть k-я строка матрицы игры доминируется (строго доминируется) r-й строкой. Мы можем r-ю строку рассматривать как выпуклую комбинацию всех строк матрицы с коэффициентами גi =0 при i ≠ r, и גr =1. Тогда доказываемое утверждение 1) следует из 1) и 2) утверждений теоремы 2.11.1.
Утверждение 2) следствия аналогичным образом вытекает из утверждений 3) и 4) теоремы 2.11.1.
Следствие 2.11.2 (о дублирующих чистых стратегиях).
Одну из двух дублирующих чистых стратегий можно удалить.
Доказательство. Если Ak и Ar — дублирующие чистые стратегии игрока А, то из определения дублирующих стратегий следует, что k-я и r-я строки матрицы игры равны, а потому каждая из них (нестрого) доминируется другой. Следовательно, одну из них можно удалить.
Рассуждения для дублирующих стратегий игрока В аналогичны.





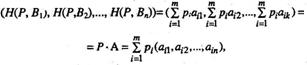 (2.11.2.)
(2.11.2.)
 (2.11.3.)
(2.11.3.) (2.11.4.)
(2.11.4.)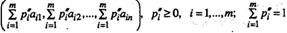 (2.11.5.)
(2.11.5.)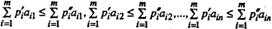 (2.11.6.)
(2.11.6.)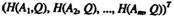 (2.11.7.)
(2.11.7.)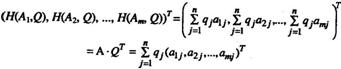 (2.11.8.)
(2.11.8.) , матрицы A с коэффициентами q1, q2,…, qn.
, матрицы A с коэффициентами q1, q2,…, qn.
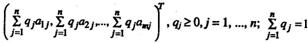
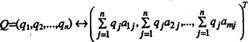 (2.11.9.)
(2.11.9.)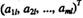 матрицы А (см. также(2.11.7.)).
матрицы А (см. также(2.11.7.)). (2.11.10)
(2.11.10)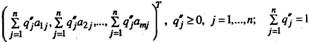 (2.11.11.)
(2.11.11.)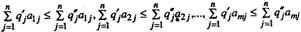 (2.11.12.)
(2.11.12.) игрока А, в которой k-я чистая стратегия Akвыбирается
игрока А, в которой k-я чистая стратегия Akвыбирается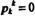 .
.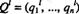 игрока В,в которой l-ячистая стратегия Вl выбирается им с нулевой вероятностью, т.е. ql=0.
игрока В,в которой l-ячистая стратегия Вl выбирается им с нулевой вероятностью, т.е. ql=0.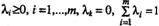 (2.11.13.)
(2.11.13.)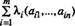 , что по определению доминирования строк означает (см.(2.11.6.)) выполнение неравенств
, что по определению доминирования строк означает (см.(2.11.6.)) выполнение неравенств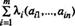 (2.11.14.).
(2.11.14.). игрока А с координатами
игрока А с координатами (2.11.15.)
(2.11.15.)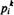 - неотрицательны и в сумме дают единицу. В самом деле, поскольку
- неотрицательны и в сумме дают единицу. В самом деле, поскольку 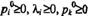 , то
, то 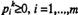 , а так как גk=0,
, а так как גk=0, 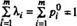 , то
, то


 ≥ V, j = 1,…,n, означают по достаточной части утверждения 1)теоремы 2.10.2, что
≥ V, j = 1,…,n, означают по достаточной части утверждения 1)теоремы 2.10.2, что 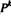 является оптимальной стратегией, причем
является оптимальной стратегией, причем  =0.
=0. , или, по определению строгого доминирования строк,
, или, по определению строгого доминирования строк, 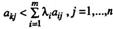 (2.11.16.).
(2.11.16.). (2.11.17.)
(2.11.17.)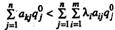 (2.11.18.)
(2.11.18.) (2.11.19.)
(2.11.19.)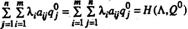 (2.11.20.)
(2.11.20.) (2.11.21)
(2.11.21)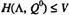 и потому из (2.11.21):
и потому из (2.11.21):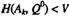 (2.11.22)
(2.11.22)


