Определение. Игра двух лиц, в которой в каждом исходе выигрыш одного из игроков равен проигрышу другого, называется антагонистической (матричной) игрой или игрой с нулевой суммой. При этом
-множество игроков состоит из двух элементов {A,B};
- FA (или FB) – функции выигрыша;
- матрица А выигрышей игрока А (она же – матрица проигрышей игрока В) называется платежной матрицей: aij=FA(y(i)A,y(j)B),
- SA,SB – множества стратегий игроков (чистых стратегий) представляют собой множества номеров строк {1,2,,m}(игрок А) и столбцов {1,2,,n}(игрок B) матрицы А.
Таким образом, конечная антагонистическая игра полностью задается платежной матрицей.
Замечание: Рассмотренные ранее конечные игры называются биматричными.
Вид матрицы биматричной игры:
|
| yВ (1)
| ...
| …
| …
| yВ (n)
|
| yА (1)
| f1 f2
|
|
|
|
|
| …
|
|
|
|
|
|
| yА(m)
|
|
|
|
|
|
Пример 1. Фирма А производит сезонный товар, который поставляется на рынок в момент времени i. Фирма В конкурирует с фирмой А (цель фирмы В – разорить фирму А) и поставляет на рынок товар в момент времени j=1,…,n – в начале каждого периода времени. Размеры фирм равны, цена товара фиксирована, а качество определяется моментом времени его поступления (чем позже товар поступил, тем он качественней). На рынке продается только более качественный товар. Доход от продаж в единицу времени равен С, число периодов времени n=4.
Строим платежную матрицу игры:
В
|
|
|
|
|
|
|
| 2С
| С
| 2С
| 3С
|
|
| 3С
| 3/2С
| С
| 2С
|
|
| 2С
| 2С
| С
| С
|
|
| С
| С
| С
| С/2
|
А
Табл. Платежная матрица (доход фирмы А равен убытку фирмы В).
Принципы оптимальности.
Пусть задана платежная матрица. Строки – стратегии игрока А; Столбцы – стратегии игрока В;
Пример 2.
А=
Добавим к ней строку и столбец:
|
| В1
| В2
| В3
| В4
| min aij
|
| А1
|
|
|
|
| 2
|
| А2
|
|
|
|
| 1
|
| А3
|
|
|
|
| 2
|
| maxaij
| 10
| 6
| 5
| 9
| minmax aij =5\maxmin aij =2
|
Определение:
α – нижняя цена игры (максимин) 
β – верхняя цена игры (минимакс) 
Теорема: 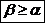
Доказательство: (очевидно)
Определение:
Если  , игра имеет цену; если
, игра имеет цену; если  , игра цены не имеет/
, игра цены не имеет/
Игра в Примеtр 2. не имеет цены.
Определение. Седловой точкой матрицы А называется такой элемент  , что
, что  .
.
Теорема. Пусть  и
и  - седловые точки матрицы А, тогда
- седловые точки матрицы А, тогда  ,
,  также являются седловыми точками и при этом
также являются седловыми точками и при этом  =
= 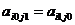
Доказательство: Рассмотрим  ,
,  и
и  ,
,  .
.
Теорема. Игра имеет цену, тогда и только тогда, когда существует седловая точка у матрицы А, т.е.  (седловая точка А) и при этом
(седловая точка А) и при этом  . Соответствующие чистые стратегии игроков (максиминная и минимаксная) являются оптимальными.
. Соответствующие чистые стратегии игроков (максиминная и минимаксная) являются оптимальными.
Доказательство: Пусть  (игра имеет цену), Ai0 – максиминная стратегия А, Aj0 – минимаксная стратегия В, тогда
(игра имеет цену), Ai0 – максиминная стратегия А, Aj0 – минимаксная стратегия В, тогда

Пусть существует седловая точка, докажем, что 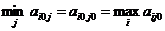 .
. 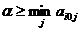 и
и 
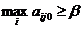 , тогда следует, что
, тогда следует, что 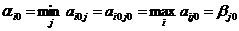 . А так как
. А так как  и
и  , и значит
, и значит  .
.
Пример 3. Две конкурирующие финансовые компании ведут переговоры с организаторами трех проектов. Задача фирмы В – профинансировать любой проект. Задача фирмы А – сорвать переговоры. Стратегии фирмы А:
1) предложить более выгодные условия;
2) опорочить фирму В.
Стратегия фирмы В: выбрать проект для финансирования.
Платежная матрица содержит значения вероятности срыва переговоров.
|
| В1
| В2
| В3
| min aij
|
| А1
| 0,7
| 0,5
| 0,3
| 0,3
|
| А2
| 0,6
| 0,9
| 0,4
| 0,4
|
| max aij
| 0,7
| 0,9
| 0,4
| 0,4\0,4
|
Находим  =0,4 и
=0,4 и  =0,4. (
=0,4. ( ).
).







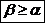
 , игра имеет цену; если
, игра имеет цену; если  , игра цены не имеет/
, игра цены не имеет/ , что
, что  .
. - седловые точки матрицы А, тогда
- седловые точки матрицы А, тогда  ,
,  также являются седловыми точками и при этом
также являются седловыми точками и при этом  =
= 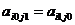
 ,
,  и
и  ,
,  .
. (седловая точка А) и при этом
(седловая точка А) и при этом  . Соответствующие чистые стратегии игроков (максиминная и минимаксная) являются оптимальными.
. Соответствующие чистые стратегии игроков (максиминная и минимаксная) являются оптимальными.
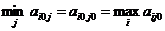 .
. 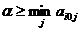 и
и 
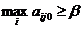 , тогда следует, что
, тогда следует, что 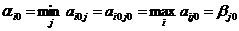 . А так как
. А так как  и
и  , и значит
, и значит  =0,4 и
=0,4 и  =0,4. (
=0,4. (


