Постановка игры в нормальной форме гораздо проще для изучения и формализации, чем игра в развернутой форме, поэтому ниже будут рассматриваться только решения игр в нормальной форме. Для игр же в развернутой форме построим формальную процедуру перехода от них к играм в нормальной форме.
Сначала введем для игры в развернутой форме понятие стратегии игрока.
Определение 3: Стратегией игрока для игры в развернутой форме называется функция, отображающая множество информационных состояний игрока на множество его ходов таким образом, что каждому информационному состоянию ставится в соответствие один из возможных в данном состоянии ходов.
Таким образом, стратегия определяет, какую альтернативу игрок должен выбирать в каждом из своих информационных состояний.
Множество стратегий каждого игрока будем обозначать X.
Элементы x декартова произведения множеств стратегий всех игроков будем называть профилями стратегий, а само декартово произведение будем обозначать X.
Для каждой вершины Q графа игры в развернутой форме и каждого профиля стратегий 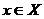 определим вероятность
определим вероятность 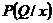 реализации данного состояния Q при использовании игроками стратегий x с помощью рекуррентной процедуры, а именно:
реализации данного состояния Q при использовании игроками стратегий x с помощью рекуррентной процедуры, а именно:
– если Q – корневая вершина, то для произвольных x, 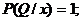
– если вершина R предшествует вершине Q в графе игры, переход из R в Q определяется природой и происходит с вероятностью p, то 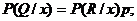
– если вершина R предшествует Q в графе игры и переход из R в Q определяется одним из игроков, то 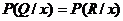 в случае, если данный переход содержится в профиле стратегий игроков, в противном случае
в случае, если данный переход содержится в профиле стратегий игроков, в противном случае 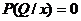 .
.
Таким способом для каждой терминальной вершины  можно определить соответствующие вероятности
можно определить соответствующие вероятности 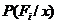 попадания в них при условии использования игроками профиля стратегий x.
попадания в них при условии использования игроками профиля стратегий x.
Теперь можно определить ожидаемые значения выигрышей игроков при использовании ими профиля x по формуле:
 , (1)
, (1)
где 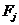 - терминальные вершины графа игры.
- терминальные вершины графа игры.
Теперь можно определить игру в нормальной форме, которая соответствует исходной игре в развернутой форме. Множество игроков новой игры совпадает с множеством игроков исходной игры, множествами действий будут определенные выше множества стратегий 
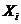 , а функция выигрыша определяется формулой (1). Эта игра вполне эквивалентна в исследовании исходной игре в развернутой форме и, если определить, что для нормальной формы игры целесообразными является набор действий
, а функция выигрыша определяется формулой (1). Эта игра вполне эквивалентна в исследовании исходной игре в развернутой форме и, если определить, что для нормальной формы игры целесообразными является набор действий 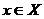 , тем самым полностью определяется и поведение игроков в исходной игре.
, тем самым полностью определяется и поведение игроков в исходной игре.
Отметим, что, поскольку выше было дано описание лишь дискретных игр в развернутой форме, то и получающиеся с помощью рассмотренной процедуры игры в нормальной форме также будут дискретными.
Пример. Рассмотрим следующую игру. Случайно выбирается некоторое число z из множества {1,2,3,4}. Каждое имеет вероятность 1/4. Игрок А, не зная результата, выбирает целое число x, а игрок Б аналогично – число y. Выигрыш определяется следующим образом: |y-z|-|x-z|, (|x-z|-|y-z|). Т.е. целью является выбор числа, наиболее близкого к z.
В этой игре каждый игрок реально имеет 4 стратегии {1,2,3,4}. (Остальные заведомо плохи.) Если, например, игрок А выбирает 1, а игрок Б выбирает 3, то выигрыш будет равен (2,-2) с вероятностью ¼, (0,0) с вероятностью ¼, (-2,2) с вероятностью ½. Ожидаемый выигрыш, таким образом, равен m(1,3)=(-1/2, 1/2). Подсчитывая все значения m(i,j)Б получим таблицу:
|
| 1
| 2
| 3
| 4
|
| 1
| (0,0)
| (-1/2, 1/2)
| (-1/2, 1/2)
| (0,0)
|
| 2
| (1/2, -1/2)
| (0,0)
| (0,0)
| (1/2, -1/2)
|
| 3
| (1/2, -1/2)
| (0,0)
| (0,0)
| (1/2, -1/2)
|
| 4
| (0,0)
| (-1/2, 1/2)
| (-1/2, 1/2)
| (0,0)
|
Таким образом, мы получили игру в нормальной форме.
Смешанные стратегии
При построении нормальной формы игры по ее развернутой форме, множества стратегий развернутой игры превращаются во множества действий игры в нормальной форме. Зачастую действие игрока в игре в нормальной форме также называют стратегией. Это не совсем верно. Обычно термин «стратегия» имеет более широкий смысл и используется для обозначения плана, который каждый игрок составляет до начала игры. Этот план описывает все действия, которые игрок будет предпринимать во всех возможных игровых состояниях. Стратегия игроков даже в игре в нормальной форме может быть более сложной, чем просто выбор одного из элементов множества действий 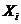 (стратегия, состоящая в выборе действия из множества
(стратегия, состоящая в выборе действия из множества 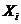 , называется чистой стратегией).
, называется чистой стратегией).
Вспомним, что в играх в развернутой форме для тех ходов, которые делала природа, указывалась вероятность того или иного ее «хода». Аналогично и игроки могут не выбирать в каждой ситуации некоторое единственное действие, а выбирать одно из действий с некоторой вероятностью. Тогда выбор игрока будет описываться вероятностным распределением на множестве возможных в данной игровой ситуации действий, которое называется смешанной стратегией. Оказывается, что такое поведение в некоторых ситуациях может привести игрока к более выгодному распределению полезностей.
Определение 4: Смешанной стратегией 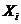 i-гo игрока
i-гo игрока 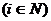 для игры в нормальной форме называется распределение вероятности на множестве действий
для игры в нормальной форме называется распределение вероятности на множестве действий 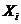 с плотностью
с плотностью 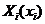 , где
, где 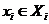 .
.
Определение 5: Вектор действий 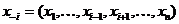 всех игроков, кроме i-гo, называется обстановкой игры для i-го игрока
всех игроков, кроме i-гo, называется обстановкой игры для i-го игрока 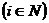 .
.
Определение 6: Распределение вероятности (с плотностью 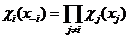 ) появления заданной обстановки при использовании игроками смешанных стратегий
) появления заданной обстановки при использовании игроками смешанных стратегий 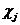 называется обстановкой в смешанных стратегиях для i-гo игрока,
называется обстановкой в смешанных стратегиях для i-гo игрока, 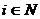 .
.
Ожидаемый выигрыш игроков при использовании ими смешанных стратегий будет вычисляться как математическое ожидание их функции выигрыша. Для дискретных игр
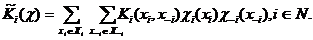
Смешанная стратегия для непрерывных игр представляет собой вероятностную меру на множестве чистых стратегий игрока. Ожидаемая полезность игроков при использовании ими смешанных стратегий будет интегралом функции полезности по декартову произведению этих вероятностных мер.
Дискретную игру, в которой игроки используют смешанные стратегии, можно привести к непрерывной игре, в которой игроки используют только чистые стратегии. Это достигается путем замены множества чистых стратегий игрока на множество его смешанных стратегий, а функции выигрыша – ее математическим ожиданием.
Тогда можно исследовать свойства новой игры в предположении, что игроки используют только чистые стратегии. Это, однако, не всегда бывает удобным, так как такой переход приводит к замене более простой, дискретной игры, более сложной – непрерывной
Приведем несколько свойств смешанных стратегий в дискретных играх.
Лемма 1. Ожидаемая полезность дискретной игры – непрерывная функция смешанных стратегий.
Теорема 2. Для произвольной обстановки в смешанных стратегиях найдется чистая стратегия, являющаяся «наилучшим ответом» на данную обстановку, то есть
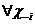
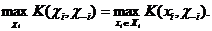
Более того, любая смешанная стратегия  ,которая содержит с ненулевой вероятностью чистую стратегию, не являющуюся лучшим ответом на обстановку
,которая содержит с ненулевой вероятностью чистую стратегию, не являющуюся лучшим ответом на обстановку 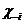 ,не будет и сама лучшим ответом на обстановку
,не будет и сама лучшим ответом на обстановку 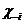
Доказательство. Множество смешанных стратегий - это компакт, в котором содержатся и чистые стратегии. Для игрока i зафиксируем обстановку в смешанных стратегиях 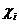 . Тогда ожидаемый выигрыш игрока i будет функцией только его смешанной стратегии
. Тогда ожидаемый выигрыш игрока i будет функцией только его смешанной стратегии 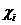 . Очевидно, существует смешанная стратегия
. Очевидно, существует смешанная стратегия 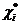 , при использовании которой ожидаемый выигрыш достигает максимума (значком
, при использовании которой ожидаемый выигрыш достигает максимума (значком 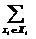 обозначается суммирование по всем элементам множества
обозначается суммирование по всем элементам множества 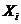 ).
).
Для стратегии 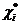 ожидаемый выигрыш есть
ожидаемый выигрыш есть
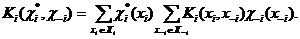 (2)
(2)
Так как 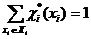 то
то 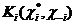 представляет собой взвешенную с весами
представляет собой взвешенную с весами 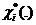 сумму величин
сумму величин

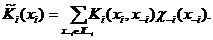 (3)
(3)
Взвешенная сумма (3) не может превышать своего максимального слагаемого, то есть существует чистая стратегия 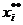 для которой
для которой 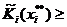
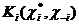 . Но в правой части этого неравенства стоит максимальный ожидаемый выигрыш, возможный при использовании смешанных стратегий. Значит, неравенство можно заменить равенством, а это, в свою очередь, значит, что максимальный ожидаемый выигрыш достигается на не которой чистой стратегии. Кроме того, если любой не максимальный элемент (3) входит в сумму (2) с ненулевым весом, то ожидаемая полезность будет строго меньше максимально возможной и смешанная стратегия не будет наилучшим ответом на обстановку
. Но в правой части этого неравенства стоит максимальный ожидаемый выигрыш, возможный при использовании смешанных стратегий. Значит, неравенство можно заменить равенством, а это, в свою очередь, значит, что максимальный ожидаемый выигрыш достигается на не которой чистой стратегии. Кроме того, если любой не максимальный элемент (3) входит в сумму (2) с ненулевым весом, то ожидаемая полезность будет строго меньше максимально возможной и смешанная стратегия не будет наилучшим ответом на обстановку 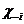 .
.
Смешанные стратегии – довольно хрупкая конструкция. Их использование в ряде практических задач неоднократно подвергалось критике. Один из аргументов против использования смешанных стратегий таков: «Применение смешанных стратегий подходит только для игр с большим числом повторений. Рассмотрим игру, которая должна быть сыграна лишь один раз. При использовании смешанных стратегий игрок должен выбирать свое решение на основании реализации случайного процесса, задаваемого распределением вероятности его смешанной стратегии. Однако эта реализация может дать стратегию, настолько «экзотическую», что ее применение в единичной игре будет малоэффективно, несмотря на теоретические обоснования эффективности такой смешанной стратегии в смысле среднего выигрыша на протяжении многих игр».
Поэтому, когда возможно, особенно при моделировании реальных систем, следует использовать только чистые стратегии.





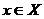 определим вероятность
определим вероятность 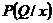 реализации данного состояния Q при использовании игроками стратегий x с помощью рекуррентной процедуры, а именно:
реализации данного состояния Q при использовании игроками стратегий x с помощью рекуррентной процедуры, а именно: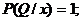
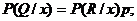
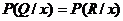 в случае, если данный переход содержится в профиле стратегий игроков, в противном случае
в случае, если данный переход содержится в профиле стратегий игроков, в противном случае 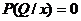 .
. можно определить соответствующие вероятности
можно определить соответствующие вероятности 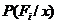 попадания в них при условии использования игроками профиля стратегий x.
попадания в них при условии использования игроками профиля стратегий x. , (1)
, (1)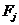 - терминальные вершины графа игры.
- терминальные вершины графа игры.
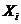 , а функция выигрыша определяется формулой (1). Эта игра вполне эквивалентна в исследовании исходной игре в развернутой форме и, если определить, что для нормальной формы игры целесообразными является набор действий
, а функция выигрыша определяется формулой (1). Эта игра вполне эквивалентна в исследовании исходной игре в развернутой форме и, если определить, что для нормальной формы игры целесообразными является набор действий 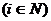 для игры в нормальной форме называется распределение вероятности на множестве действий
для игры в нормальной форме называется распределение вероятности на множестве действий 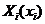 , где
, где 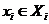 .
.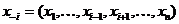 всех игроков, кроме i-гo, называется обстановкой игры для i-го игрока
всех игроков, кроме i-гo, называется обстановкой игры для i-го игрока 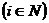 .
.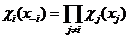 ) появления заданной обстановки при использовании игроками смешанных стратегий
) появления заданной обстановки при использовании игроками смешанных стратегий 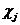 называется обстановкой в смешанных стратегиях для i-гo игрока,
называется обстановкой в смешанных стратегиях для i-гo игрока, 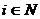 .
.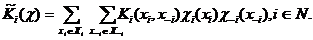
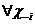
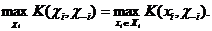
 ,которая содержит с ненулевой вероятностью чистую стратегию, не являющуюся лучшим ответом на обстановку
,которая содержит с ненулевой вероятностью чистую стратегию, не являющуюся лучшим ответом на обстановку 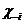 ,не будет и сама лучшим ответом на обстановку
,не будет и сама лучшим ответом на обстановку 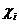 . Тогда ожидаемый выигрыш игрока i будет функцией только его смешанной стратегии
. Тогда ожидаемый выигрыш игрока i будет функцией только его смешанной стратегии 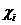 . Очевидно, существует смешанная стратегия
. Очевидно, существует смешанная стратегия 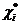 , при использовании которой ожидаемый выигрыш достигает максимума (значком
, при использовании которой ожидаемый выигрыш достигает максимума (значком 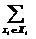 обозначается суммирование по всем элементам множества
обозначается суммирование по всем элементам множества 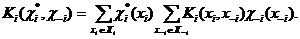 (2)
(2)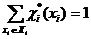 то
то 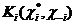 представляет собой взвешенную с весами
представляет собой взвешенную с весами 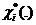 сумму величин
сумму величин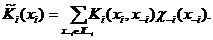 (3)
(3)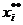 для которой
для которой 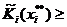
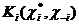 . Но в правой части этого неравенства стоит максимальный ожидаемый выигрыш, возможный при использовании смешанных стратегий. Значит, неравенство можно заменить равенством, а это, в свою очередь, значит, что максимальный ожидаемый выигрыш достигается на не которой чистой стратегии. Кроме того, если любой не максимальный элемент (3) входит в сумму (2) с ненулевым весом, то ожидаемая полезность будет строго меньше максимально возможной и смешанная стратегия не будет наилучшим ответом на обстановку
. Но в правой части этого неравенства стоит максимальный ожидаемый выигрыш, возможный при использовании смешанных стратегий. Значит, неравенство можно заменить равенством, а это, в свою очередь, значит, что максимальный ожидаемый выигрыш достигается на не которой чистой стратегии. Кроме того, если любой не максимальный элемент (3) входит в сумму (2) с ненулевым весом, то ожидаемая полезность будет строго меньше максимально возможной и смешанная стратегия не будет наилучшим ответом на обстановку 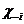 .
.

