

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Интересное:
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Рассмотрим важный частный случай игр двух лиц – так называемые игры с нулевой суммой. Игры с нулевой суммой имеют вид  , т.е. игроки 1 и 2 являются строгими антагонистами. Обозначим такую игру через
, т.е. игроки 1 и 2 являются строгими антагонистами. Обозначим такую игру через  , где
, где  - платеж, который игрок 1 максимизирует, а игрок 2 минимизирует.
- платеж, который игрок 1 максимизирует, а игрок 2 минимизирует.
Тогда осторожные стратегии могут быть заданы так:
 ;
;
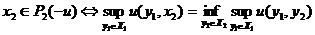 .
.
Числа  и
и  являются соответственно максимальным гарантированным выигрышем игрока 1 (верхней ценой игры) и минимальным гарантированным проигрышем игрока 2 (нижней ценой игры). Они связаны неравенством
являются соответственно максимальным гарантированным выигрышем игрока 1 (верхней ценой игры) и минимальным гарантированным проигрышем игрока 2 (нижней ценой игры). Они связаны неравенством
 (3)
(3)
Для доказательства (3) фиксируем произвольные 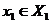 ,
,  и заметим, что
и заметим, что
 ,
,
откуда следует
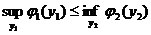
Если выполнено равенство  , то говорят, что
, то говорят, что 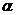 есть цена (значение) игры
есть цена (значение) игры  . Если (3) строгое неравенство, то говорят, что игра не имеет цены.
. Если (3) строгое неравенство, то говорят, что игра не имеет цены.
Теорема. Пусть  - игра двух лиц с нулевой суммой. Если игра имеет цену, то она несущественна. Обратно, предположим, что
- игра двух лиц с нулевой суммой. Если игра имеет цену, то она несущественна. Обратно, предположим, что  ,
,  компактны,
компактны,  непрерывна; тогда, если
непрерывна; тогда, если  несущественна, то она имеет цену.
несущественна, то она имеет цену.
Доказательство. Пусть  имеет цену, и пусть исход
имеет цену, и пусть исход 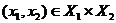 таков, что
таков, что
 ,
,
 (4)
(4)
Поскольку (3) в силу существования цены обращается в равенство, то эти два неравенства на самом деле тоже равенства, и первое утверждение доказано.
Предположим теперь, что (3) – строгое неравенство. В силу предположений о компактности и непрерывности леммы 3 можно выбрать пару 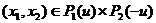 . Эта пара удовлетворяет системе (4), в которой хотя бы одно из неравенств строгое, и поэтому игра
. Эта пара удовлетворяет системе (4), в которой хотя бы одно из неравенств строгое, и поэтому игра  не может быть несущественной.
не может быть несущественной.
Для несущественных игр с нулевой суммой пара оптимальных стратегий является Седловой парой.
Определение. Седловая пара в игре двух лиц с нулевой суммой  есть такая пара
есть такая пара  , что
, что

Обозначим через S множество Седловых пар (возможно, пустое).
Теорема. Пусть 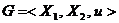 - игра двух лиц с нулевой суммой. Если G имеет цену, то исход игры является парой оптимальных стратегий тогда и только тогда, когда он является седловой парой:
- игра двух лиц с нулевой суммой. Если G имеет цену, то исход игры является парой оптимальных стратегий тогда и только тогда, когда он является седловой парой:  Если G не имеет цены, то нет и седловой пары.
Если G не имеет цены, то нет и седловой пары.
Доказательство. Предположим сначала, что игра имеет цену, тогда по теореме 1 она несущественна. По свойству 3 теоремы 1 получаем включение 
Обратно, выберем седловую пару  . Из определения 9.9
. Из определения 9.9

В силу (3) эти четыре неравенства обращаются в равенства, значит, хi – осторожная стратегия игрока i (i=1,2).
Теоремы показывают, что наличие или отсутствие цели игры является ключевой характеристикой игры с нулевой суммой. Если игра обладает ценой, то оптимальные стратегии существуют и определяются эквивалентно двумя способами: изолированно (как осторожные стратегии) и одновременно обоими игроками (как седловые пары).
Пример Пусть у обоих игроков имеется по три стратегии. Функция  задается 3х3-матрицей, в которой строки соответствуют элементам множества Х1, а столбцы – элементом множества Х2. Рассмотрим следующую функцию выигрыша:
задается 3х3-матрицей, в которой строки соответствуют элементам множества Х1, а столбцы – элементом множества Х2. Рассмотрим следующую функцию выигрыша:
| -2 | -3 | ||||
| + | -1 | -1 | |||
| -3 | -2 | ||||
| + | + | ||||
У игрока 1 одна оптимальная стратегия (+), а у игрока 2 их две. Цена игры равна -1.
Пример. «раз-два-три». Игроки одновременно выбирают одну из трех стратегий «раз», «два» или «три». Выигрыш первого игрока положителен, если он правильно угадал выбор второго игрока, и нуль в противном случае. Выигрыши задаются матрицей:
| раз | |||
| два | |||
| три | |||
| раз | два | три |
Гарантированный выигрыш игрока 1 равен 0, и любая его стратегия является осторожной, так как гарантирует только 0.
Гарантированный проигрыш игрока 2 равен 1, и у него единственная осторожная стратегия «раз» (поскольку «два» и «три» могут дать проигрыш в размере 2 или 3).
Таким образом, цена игры здесь отсутствует.
Осторожное поведение игроков основано на предположении об их «полной изолированности», согласно которому каждый игрок ориентируется только на свою собственную функцию выигрыша и не обращает внимания на функции выигрыша остальных игроков.
|
|
|

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...
© cyberpedia.su 2017-2025 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!