Пусть задана игра ис природой
|
| П1
| …
| Пn
|
| A1
|
|
|
|
| …
|
| aij
|
|
| An
|
|
|
|
| qi
| q1
|
| qn
|
Определение:
Показателем эффективности стратегии Аi называется величина 
Стратегия игрока называется максимальной, если показатель эффективности ее максимален. Ai0 – оптимальна (в соответствии с К1) => max āi = āi0.
 Определение:
Определение:
Выигрыш игрока при использовании им смешанной стратегии P=
Равен 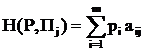
Определение:
Показателем эффективности игрока А (в соответствии с К1) называется величина

Определение:
Стратегия P0 игрока А назыается оптимальной на множестве Sa (в соответствии с К1) если
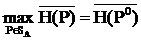
Теорема.
Если стратегия Аio оптимальна на множестве чистых стратегий Sca (в соответствии с К1), то она оптимальна и на множестве смешанных стратегий Sa (в соответствии с К1).
Доказательство.

Если верно, что  , то =>
, то => 
Т.к.  .
. 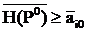
Критерий Байеса относительно риска (К2).
Определение:
Показателем неэффективности Аi (в соответствии с К2) есть величина
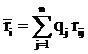 , ║rij║ = Ra.
, ║rij║ = Ra.
Стратегия Аi0 игрока А называется оптимальной, если 
Определение:
Риском, при использовании игроком А стратегии P и при Пi называется:

Определение:
Показатель эффективности стратегии В игрока А (в соответствии с К2) называется величина:

Определение:
Смешанные стратегии P0 игрока А называется оптимальной (в соответствии с К2), если

Теорема.
Стратегия Аio игрока А, оптимальная (в соответствии с К2) на множестве ScА (множество рисков), будет оптимальной и на SА (множество смешанных стратегий).
Доказательство:

Докажем это неравенство в другую сторону.
Пусть  ,
, 




Итак, 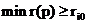
≤
Теорема об эквивалентности К1 и К2.
Рассмотрим показатели эффективности стратегий относительно риска:
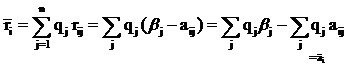
 достигает своего минимума если
достигает своего минимума если  достигает своего максимума.
достигает своего максимума.
Критерий Лапласса относительно выигрыша/риска.
Все состояния природы считаются равновероятными.
 , j = 1,..., n
, j = 1,..., n
Далее, все формулировки аналогичны критериям Байеса.
Критерий относительных значений вероятностей состояний природы с учетом рисков. Так же, как и в случае предыдущего критерия располагаем неизвестные вероятности состояний природы в виде монотонной последовательности пропорционально последовательности положительных чисел τ1,..., τn, т.е. имеем равенство (2.20.27), из которого для вероятностей qi, i=1,…, n, выводим формулу (2.20.31)
Критерий Байеса относительно рисков при вероятностях состояний природы (2.20.31) назовем критерием относительных значений вероятностей состояний природы с учетом рисков. При этом показатель неэффективности стратегии подсчитывается по формуле (2.20.10), вероятности qi,..., qn в которой представлены формулой (2.20.31):
 (2.20.38)
(2.20.38)
где rij - риски, заполняющие матрицу (2.20.9).
Поскольку величина  не зависит от номера i=l,..., n, то в качестве показателя неэффективности стратегии Аi,- поданному критерию можно рассматривать величину
не зависит от номера i=l,..., n, то в качестве показателя неэффективности стратегии Аi,- поданному критерию можно рассматривать величину
 (2.30.29)
(2.30.29)
Оптимальной среди чистых стратегий по обсуждаемому критерию является
стратегия с минимальным показателем неэффективности (2.20.39).
Показателем неэффективности смешанной стратегии P=(pi,..., рm) по рассматриваемому критерию является величина  , определяемая формулой (2.20.13), в которой вероятности qj, j=l,.., n, задаются формулой (2.20.31):
, определяемая формулой (2.20.13), в которой вероятности qj, j=l,.., n, задаются формулой (2.20.31):
 (2.20.40)
(2.20.40)
где риск r(P, Пj) применения смешанной стратегий Р при состоянии природы Пj определяется формулой (2.20.12).
Оптимальной среди всех смешанных стратеги Р множества SA по данному критерию является стратегия, для которой показатель неэффективности (2.20.40) минимален.
Теорема 2.20.2 при вероятностях состояний природы (2.20.31) говорит о том, что чистая стратегия, оптимальная среди чистых по критерию относительных значений вероятностей состояний природы с учетом рисков является оптимальной по тому же критерию и среди всех смешанных стратегий.
Пример 2.20.6. В условиях примера 2.20.5 найдем оптимальную стратегию по критерию относительных значений вероятностей состояний природы с учетом рисков.
Выпишем матрицу рисков (2.20.26) (без последнего столбца) для платежной матрицы (2.20.37) (без последнего столбца) и добавим к ней столбец показателей неэффективности стратегий ri, вычисленных по формуле (2.20.39):
| Ai \ Пj
| П1
| П2
| П3
| П4
| 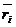
|
| A1
|
|
|
|
|
|
| A2
|
|
|
|
|
|
| A3
|
|
|
|
|
|
| A4
|
|
|
|
|
|
(2.20.41)
Так, например,  =4*7+3*1+2*6+1*4=47.
=4*7+3*1+2*6+1*4=47.
Из последнего столбца матрицы (2.20.41) мы видим, что
минимальным показателем неэффективности  =12 обладает стратегия А3 и, значит, она по критерию относительных значении вероятностей состояний природы с учетом рисков является оптимальной.
=12 обладает стратегия А3 и, значит, она по критерию относительных значении вероятностей состояний природы с учетом рисков является оптимальной.
Результаты в примерах 2.20.5 и 2.20.6 совпадают. Теорема 2.20.3 при вероятностях состояний природы, вычисляемых по формуле (2.20.31), показывает, что это не случайность, а именно показывает, что критерии относительных значений вероятностей состояний природы с учетом выигрышей и с учетом рисков эквивалентны. Для лучшей обозримости сведем рассмотренные в этом параграфе критерии в таблице.
Таблица 2.20.1
Критерии относительно выигрышей
| №№
п/п
| Критерий
| Вероятности состояний природы

| Показатель эффективности стратегии

|
| 1B
| Критерий Бейса относительно выигрышей
| 
| 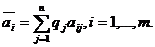
|
| 2B
| Критерий Лапласа относительно выигрышей
| 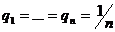
| 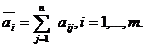
|
| 3B
| Критерий относительный значений вероятностей
| 

| 
|
По каждому из этих критериев оптимальной является стратегия  , показатель эффективности которой
, показатель эффективности которой  , т.е.
, т.е.  =
= 
 . Очевидно, что каждый из этих критериев является по существу критерием Байеса относительно выигрышей и отличаются они друг от друга лишь способом добывания информации о вероятностях состояний природы.
. Очевидно, что каждый из этих критериев является по существу критерием Байеса относительно выигрышей и отличаются они друг от друга лишь способом добывания информации о вероятностях состояний природы.
По каждому из этих критериев является стратегия  показатель
показатель
неэффективности  который минимален, т.е.
который минимален, т.е.  =
= 
 .
.
Каждый из этих критериев является критерием Байеса относительно рисков и отличаются они друг от друга только способом получения информации о вероятностях состояний природы.
Таблица 2.20.21
Критерии относительно рисков состояний природы с учетом рисков
| №№
п/п
| Критерий
| Вероятности состояний природы

| Показатель эффективности стратегии

|
| 1P
| Критерий Бейса относительно рисков
| 
| 
|
| 2P
| Критерий Лапласа относительно рисков
| 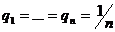
| 
|
| 3P
| Критерий относительный значений вероятностей состояний природы с учетом рисков
| 

| 
|
Наконец, напомним, что, как следует из теоремы 2.20.3, критерии 1В, 2В, 3В эквивалентны соответственно критериям 1р,2р,3р.
Заканчивая обсуждение способов принятия решения в условиях риска, мы видим, что информация о вероятностях состояний природы может быть как объективной, так и субъективной. Оптимальные стратегии, определенные на основе субъективной оценки вероятностей состояний природы, в общем случае также оказываются субъективными. Степень субъективности оптимальных решений можно уменьшить, если вероятности состояний природы, назначенные одним экспертом, заменить на средние вероятностей, назначенных различными экспертами независимо друг от друга.
 ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
В предыдущей лекции мы рассмотрели подходы к принятию решений в условиях риска, т.е. в условиях, когда мы существенно использовали вероятности состояний природы, добытые тем или иным путем.
В настоящем параграфе мы обсудим некоторые критерии принятия оптимальных решений в условиях неопределенности, т.е. когда вероятности, с которыми природа может принимать то или иное состояние, неизвестны и отсутствует всякая возможность получения о них какой-либо статистической информации.
Пусть в игре с природой П игрок А обладает m возможными чистыми стратегиями А1...,Аm, а природа П может находится в одном из n состояний П1..., Пn. Пусть (20.1) является матрицей выигрышей игрока А.
Обобщенный критерий пессимизма-оптимизма Гурвица относительно выигрышей с коэффициентами λ1,λ2,λ3,…λn.
Переставим выигрыши аi1,аi2,...,аin при каждой стратегии Ai, (т.е. элементы каждой строки матрицы (2.20.1)), расположив их в неубывающем порядке, и обозначим элементы полученной матрицы через bij, а саму матрицу — через B:
| Bi \ j
|
|
| …
| n
|
| B1
| b11
| b12
| …
| b1n
|
| B2
| b21
| b21
| …
| b2n
|
| …
| …
| …
| …
| …
|
| Bm
| bm1
| bm2
| …
| bmn
|
B =
Таким образом,
 (2.21.1)
(2.21.1)
Каждая строка B i матрицы В является перестановкой выигрышей при стратегии Ai, (i = 1,..., m). Не исключена возможность, что для некоторых номеров i и j будет иметь место равенство bij = aij. В силу неравенств (2.21.1), в первом столбце матрицы В стоят минимальные выигрыши при каждой стратегии
 (2.21.2)
(2.21.2)
а в последнем n-м столбце — максимальные выигрыши при каждой стратегии
 (2.21.3)
(2.21.3)
Пусть числа λ1,λ2,λ3,…λn, удовлетворяют условиям
 и
и  (2.21.4)
(2.21.4)
Показателем эффективности стратегии Аi по рассматриваемому критерию назовем число
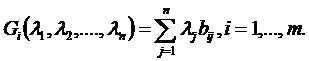 (2.21.5)
(2.21.5)
Из этого определения видно, что показатель эффективности стратегии Аi, учитывает все выигрыши при этой стратегии bi1,..., bin и зависит от чисел λi,j=1,..., n, удовлетворяющих условиям (2.21.4).
Выражение (2.21.5) является выпуклой комбинацией выигрышей ни строки матрицы В с коэффициентами λi,j=1,..., n,. В обозначении  можно было бы не указывать один из коэффициентов, например, λ1, поскольку он однозначно определяется остальными n-1 коэффициентами из нормировочного равенства (2.21.4).
можно было бы не указывать один из коэффициентов, например, λ1, поскольку он однозначно определяется остальными n-1 коэффициентами из нормировочного равенства (2.21.4).
Обобщенным критерием пессимизма-оптимизма Гурвица относительно выигрышей с коэффициентами  назовем критерий, по которому оптимальной среди чистых стратегий считается стратегия
назовем критерий, по которому оптимальной среди чистых стратегий считается стратегия  . с максимальным показателем эффективности (2.21.5), т.е.
. с максимальным показателем эффективности (2.21.5), т.е.




Числа
 и
и  (2.21.6)
(2.21.6)
назовем показателями соответственно пессимизма и оптимизма. В обозначениях (2.21.6) индекс «р» — первая буква английского pessimism [, pesi'mizm], индекс «о» — первая буква английского optimism ['optimizm], a  — целая часть числа
— целая часть числа 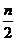 , т.е. наибольшее целое число, непревосходящее числа n/2; очевидно, что
, т.е. наибольшее целое число, непревосходящее числа n/2; очевидно, что

, если n-число четное ( 2)
2)
, если n-число нечетное ( 2)
2)
Коэффициенты λ1,λ2,λ3,…λn выбираются из субъективных соображений следующим образом: чем опаснее ситуация, тем больше возникает желание в ней подстраховаться, тем больше, т.е. ближе к единице, должен быть коэффициент пессимизма λp (см. 2.21.6) и, следовательно, тем меньше, т.е. ближе к нулю, будет коэффициент оптимизма λo. В безопасной ситуации коэффициенты λ1,λ2,λ3,…λn выбираются так, чтобы показатель пессимизма λp был ближе к нулю, а показатель оптимизма λo— ближе к единице. Таким образом, показатели пессимизма λp и оптимизма λo в данном критерии выражают количественную меру соответственно пессимизма и оптимизма игрока A, выбирающего коэффициенты λ1,…λn.
Если показатель оптимизма λo > 1/2 и, следовательно показатель пессимизма λp< < 1/2, то критерий более «оптимистический», чем «пессимистический»; если, наоборот, показатель оптимизма λo < ½ и, следовательно показатель пессимизма λр > ½, то критерий более пессимистический чем оптимистический; если же показатели оптимизма и пессимизма равны: λo=λр=1/2, то критерий можно считать реалистическим.
 Чуть позже мы предложим некоторый формализованный метод выбора коэффициентов λ1,λ2,λ3,…λn, учитывающий все выигрыши игрока А.
Чуть позже мы предложим некоторый формализованный метод выбора коэффициентов λ1,λ2,λ3,…λn, учитывающий все выигрыши игрока А.
Если bij=aij для всех i=1,...,n и j=1,...,n, т.е. если матрица В совпадает с матрицей (2.20.1), то коэффициенты λ1,…λn, можно формально интерпретировать как вероятности состояний природы: q1=λ1...,qn=λn, и тогда показатель эффективности стратегии Ai, по обобщенному критерию Гурвица относительно выигрышей, определяемый формулой (2.21.5), превращается в показатель эффективности стратегии Ai по критерию Байеса относительно выигрышей, вычисляемый по формуле (2.20.2):  . Следовательно, в этом случае, обобщенный критерий Гурвица относительно выигрышей превращается в критерий Байеса относительно выигрышей.
. Следовательно, в этом случае, обобщенный критерий Гурвица относительно выигрышей превращается в критерий Байеса относительно выигрышей.
Если коэффициенты  , то их можно формально трактовать как вероятности равновероятных состояний природы и из (2.21.5) получим:
, то их можно формально трактовать как вероятности равновероятных состояний природы и из (2.21.5) получим:

Но поскольку bi1,...,bin есть перестановка элементов ai1,...,ain i-строки матрицы (2.20.1), то  и, следовательно,
и, следовательно,
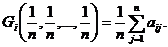
т.е. показатель эффективности стратегии Ai по обобщенному критерию Гурвица относительно выигрышей совпадает, как это следует из равенства (2.20.23), с показателем эффективности стратегии Ai - по критерию Лапласа относительно выигрышей. Значит, обобщенный критерий пессимизма-оптимизма Гурвица относительно выигрышей с равными коэффициентами λ1=…= λn=1/2, превращается в критерий Лапласа относительно выигрышей.
Критерий Вальда (критерий крайнего пессимизма).
Критерий Вальда есть частный случай обобщенного критерия Гурвица относительно выигрышей со специальными коэффициентами
λ1=1,λ2=0…= λn=0 (2.21.7)
которые, очевидно, удовлетворяют условиям (21.4).
Подставляя значения коэффициентов (2.21.7) в формулу (2.21.5) и учитывая (2.21.2), получим показатель эффективности стратегии Аi- по критерию Вальда:
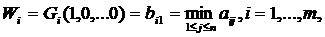 (2.21.8)
(2.21.8)
представляющий собой минимальный выигрыш игрока А при применении им стратегии Ai. Оптимальной среди чистых стратегий по критерию Вальда является, таким образом, стратегия  , имеющая максимальный показатель эффективности (2.21.8):
, имеющая максимальный показатель эффективности (2.21.8):

Другими словами, оптимальной среди чистых стратегий по критерию Вальда считается та чистая стратегия, при которой минимальный выигрыш является максимальным среди минимальных выигрышей всех чистых стратегий. Таким образом, оптимальная стратегия по критерию Вальда гарантирует при любых состояниях природы выигрыш, не меньший, чем максимин
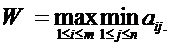
Из (2.21.7) и (2.21.6) получаем, что для критерия Вальда показатель пессимизма λр=1 а показатель оптимизма λо=0. Это говорит о том, что критерий Вальца является критерием крайнего пессимизма, ибо ориентирует игрока А на наихудшие для него состояния природы и, следовательно, на крайне осторожное, осмотрительное поведение при выборе стратегий. Хотя арабская пословица и гласит «Кто боится собственной тени, тому нет места под солнцем», тем не менее этот критерий уместен в тех случаях, когда игрок А не столько хочет выиграть, сколько не хочет проиграть. Принципом критерия Вальда часто пользуются в обиходе, что подтверждается такими поговорками, как «Семь раз отмерь—один раз отрежь», «Береженного бог бережет», «Лучше синица в руках, чем журавль в небе».
Максимаксный критерий (критерий крайнего оптимизма). Противоположностью критерию Вальда является так называемый максимаксный критерий, представляющий собой также частный случай обобщенного критерия Гурвица относительно выигрышей, когда коэффициенты λ1,λ2,…, λn выбираются следующим образом:
λ1=…=λn-1=0, λn=1 (2.21.9)
Коэффициенты (2.21.9) удовлетворяют условиям (2.21.4). Если эти коэффициенты подставить в (2.21.5) и учесть (2.21.3), то получим формулу для показателя эффективности стратегии Ai, по максимаксному критерию:
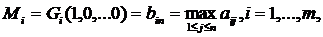 (2.21.10)
(2.21.10)
Значит, в качестве показателя эффективности стратегии Ai по максимаксному критерию выбирается максимальный выигрыш при этой стратегии.
Тогда оптимальной среди чистых стратегий по максимаксному критерию является стратегия  с максимальным показателем эффективности„(2.21.10):
с максимальным показателем эффективности„(2.21.10):

т.е. стратегия, максимальный выигрыш при которой максимален среди максимальных выигрышей всех чистых стратегий. По-другому можно сказать, что оптимальной будет та чистая стратегия, при которой (хотя-бы) один из выигрышей
является максимальным среди выигрышей всех чистых стратегии. Оптимальная по максимаксному критерию стратегия гарантирует игроку А возможность наибольшего выигрыша, равного максимаксу

Подставляя коэффициенты (2.21.9) в (2.21.6), найдем для максимаксного критерия показатель пессимизма λ p =0 и показатель оптимизма λ o =1. Таким образом, максимаксный критерий является критерием крайнего оптимизма, так как ориентирует лицо, принимающее решение, (игрока А) на наилучшие, благоприятнейшие для него состояния природы и, как следствие отсюда — на порой неоправданно легкомысленное, шапкозакидательское поведение при выборе стратегий. Вместе с тем, в некоторых случаях этим критерием пользуются осознанно, например, в ситуации, когда перед игроком А стоит дилемма: либо получить наибольший выигрыш, либо стать банкротом.
Критерий пессимизма-оптимизма Гурвица относительно выигрышей, с показателем оптимизма 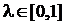
Данный критерий является как бы промежуточным между критериями крайнего пессимизма и крайнего оптимизма и представляет собой частный случай обобщенного критерия Гурвица относительно выигрышей с коэффициентами
 (2.21.11)
(2.21.11)
удовлетворяющими, очевидно, условиям (2.21.4).
Из (2.21.11), (2.21.5), (2.21.2) и (2.21.3) следует, что показателем эффективности стратегии А, по рассматриваемому критерию является величина
 (2.21.12)
(2.21.12)
Оптимальной же стратегией по этому критерию считается стратегия А i 0 с максимальным показателем эффективности (2.21.12):

Из (2.21.11) и (2.21.6) получаем, что показатели пессимизма и оптимизма в этом критерии равны соответственно λ р =1-λ и λ o =λ. При λ=0 мы из критерия Гурвица получаем критерий Вальда, а при λ=1 — максимаксный критерий. Чем ближе к нулю показатель оптимизма λ, тем ближе к единице показатель пессимизма 1-λ, и тем меньше оптимизма и больше пессимизма. И наоборот, чем ближе λ к единице, тем больше оптимизма и меньше пессимизма. Если показатель оптимизма 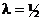 , то и показатель пессимизма
, то и показатель пессимизма 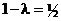 . В этом случае показатель эффективности стратегии Аi, как следует из формулы (2.21.12), примет вид:
. В этом случае показатель эффективности стратегии Аi, как следует из формулы (2.21.12), примет вид:
 (2.21.13)
(2.21.13)
а так как множитель 1/2 в правей части этого равенства не зависит oт номера i, то в качестве показателя эффективности стратегии А i по критерию пессимизма-оптимизма Гурвица относительно выигрышей с показателем оптимизма λ=1/2 можно рассмотреть правую часть равенства (2.21.13) без коэффициента 1/2:

Отметим, что критерий Вальда, максимаксный критерий и критерий пессимизма-оптимизма Гурвица относительно выигрышей с показателем оптимизма  не учитывают всех выигрышей игрока А при каждой его стратегии: критерий Вальда принимает во внимание только минимальные выигрыши при каждой стратегии, максимаксный критерий учитывает лишь максимальные выигрыши при каждой стратегии, а критерий пессимизма-оптимизма Гурвица относительно выигрышей с показателем оптимизма
не учитывают всех выигрышей игрока А при каждой его стратегии: критерий Вальда принимает во внимание только минимальные выигрыши при каждой стратегии, максимаксный критерий учитывает лишь максимальные выигрыши при каждой стратегии, а критерий пессимизма-оптимизма Гурвица относительно выигрышей с показателем оптимизма  опирается на минимальные и максимальные выигрыши. В отличие от этого обобщенный критерий Гурвица учитывает все выигрыши при каждой стратегии игрока А, используя тем самым полную информацию об игре, поскольку вся имеющаяся информация об игре с природой в условиях неопределенности содержится в матрице выигрышей игрока A.
опирается на минимальные и максимальные выигрыши. В отличие от этого обобщенный критерий Гурвица учитывает все выигрыши при каждой стратегии игрока А, используя тем самым полную информацию об игре, поскольку вся имеющаяся информация об игре с природой в условиях неопределенности содержится в матрице выигрышей игрока A.
Перейдем к вопросу о формализации метода выбора коэффициентов λ1, λ2,..., λ n в обобщенном критерии Гурвица относительно выигрышей.
Пусть
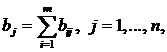 (2.21.14)
(2.21.14)
— сумма выигрышей, стоящих в j -м столбце матрицы В;
 (2.21.15)
(2.21.15)
— среднее значение выигрышей bi j, стоящих в j-м столбце матрицы В;
 (2.21.16)
(2.21.16)
— сумма всех выигрышей матрицы В, или, что то же, сумма всех выигрышей матрицы А (см. (2.20.1)).
Просуммировав неравенства (2.21.1) по индексу i от 1 до m, получим с учетом обозначений (2.21.14):

откуда, в обозначениях (2.21.15):
 (2.21.17)
(2.21.17)
В случае опасной ситуации выбор стратегии игроком А должен быть осторожным, «направленным» в сторону убывания выигрышей. Поэтому коэффициенты λ j по мере убывания выигрышей должны возрастать. Учитывая (2.21.17), эти коэффициенты можно выбрать обратно пропорциональными средним выигрышам (21.15):
 (2.21.18)
(2.21.18)
Так как неравенства (2.21.17) можно переписать так:

то принцип (2.21.18) выбора коэффициентов λ j, j =1,..., n, можно назвать «принципом невозрастания средних выигрышей».
Выразим коэффициенты λ j , j =1,..., n, через выигрыши bij.
Из (2.21.18):

откуда
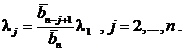 (2.21.19)
(2.21.19)
Подставляя эти выражения в нормировочное равенство (2.21.4), получим
 ,
,
откуда
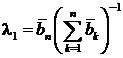
или, в силу (2.21.15) и (2.21.16):

Подставляя найденное значение λ1 в (2.21.19) и используя (2.21.15), будем иметь:
 (2.21.20)
(2.21.20)
Таким образом, выбирая в опасной ситуации коэффициенты λ j, j =1,..., n, в соответствии с принципом невозрастания средних выигрышей, мы видим, что j -й коэффициент λ j представляет собой отношение суммы bn - j +1 элементов bi , n - j +1, i =1,.... m, стоящих в (n - j +1)-м столбце матрицы B, к сумме b всех ее элементов, т.е. коэффициент λ j есть доля суммы элементов (n - j +1)-го столбца в сумме всех элементов матрицы В.
В случае безопасной ситуации коэффициенты λ j при возрастании выигрышей должны возрастать; поэтому их можно выбрать по «принципу неубывания средних выигрышей» прямо пропорционально средним выигрышам (2.21.15):

Аналогичным способом можно показать, что в данном случае коэффициенты λ j выражаются через выигрыши следующим образом:
 (2.21.21)
(2.21.21)
Распространим критерий Гурвица относительно выигрышей, а значит и его частные случаи — критерии Вальда и максимаксный критерий, на смешанные стратегии.
Пусть SA - множество всех смешанных (в том числе и чистых) стратегий игрока A и Р =(р 1,…, pm) — некоторая смешанная стратегия игрока А из множества  . Тогда выигрыш игрока А при применении им смешанной стратегии P =(p 1,…, pm), соответствующий состоянию природы Пj, равен
. Тогда выигрыш игрока А при применении им смешанной стратегии P =(p 1,…, pm), соответствующий состоянию природы Пj, равен
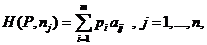 (2.21.26)
(2.21.26)
где ai j, i =1,…, m; j =1,…, n, — элементы матрицы (2.20.1).
Показателем эффективности смешанной стратегии Р = (p 1,..., pm) по критерию пессимизма-оптимизма Гурвица относительно выигрышей с показателем оптимизма 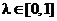 назовем число
назовем число
 (2.21.27)
(2.21.27)
где
 и
и 
— соответственно минимальный и максимальный выигрыши игрока А при использовании им смешанной стратегии Р.
Так как каждой смешанной стратегии Р соответствуют единственные значения минимального и максимального выигрышей, то W(P) и М(Р), а, следовательно, и G(P; λ), являются числовыми функциями векторного аргумента Р = (p 1,..., pm) определенными на множестве SA.
Если, в частности, смешанная стратегия Р = (p 1,..., pm) является чистой Аk, то pi = 0 при i ≠ к, и рk =1; следовательно, по формуле (2.21.26), H (P, Пj) = Н (Ак, Пj) = akj и показатель эффективности G (P; λ) превращается в показатель эффективности Gk(λ) чистой стратегии Аk, определяемый формулой (2.21.12) при i = k.
Оптимальной среди всех смешанных стратегий множества SA по критерию пессимизма-оптимизма Гурвица относительно выигрышей с показателем оптимизма 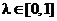 назовем стратегию
назовем стратегию  с максимальным показателем эффективности G(P; λ):
с максимальным показателем эффективности G(P; λ):
 (2.21.28)
(2.21.28)
В связи с бесконечностью множества SA встает вопрос о существовании определяемой формулой (2.21.28) оптимальной стратегии Р 0, т.е. о достижимости функцией G (P; λ) своей верхней грани на множестве SA. Ответ на этот вопрос положителен. Для доказательства этого сначала докажем непрерывность функций W (P) и М (Р) на множестве SA.
Функция H (P, Пj), задаваемая формулой (2.21.26), линейна и, следовательно, непрерывна по аргументу P на множестве SA, т.е. для любого ɛ>0 найдется δ j >0, зависящее от ɛ, номера j и точки P, такое, что для любой точки 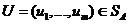 , отстоящей от точки P на расстоянии, не большем чем δ j: ρ(P, U) ≤ δ j, справедливо неравенство
, отстоящей от точки P на расстоянии, не большем чем δ j: ρ(P, U) ≤ δ j, справедливо неравенство

которое можно переписать так :

или так:

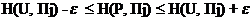 . (2.21.29)
. (2.21.29)
Под paccтоянием  понимается обычное евклидово paccтояние в пространстве Rm, определяемое формулой
понимается обычное евклидово paccтояние в пространстве Rm, определяемое формулой

Eсли точка  такова, что
такова, что
 (2.21.30)
(2.21.30)
то неравенство 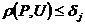 ,будет выполняться для каждого j = 1,..., n, и, следовательно, для каждого j = 1,..., n, 6yдут выполняться неравенства (2.21.29).
,будет выполняться для каждого j = 1,..., n, и, следовательно, для каждого j = 1,..., n, 6yдут выполняться неравенства (2.21.29).
Taк как

то из левого неравенства (2.21.29) получим:

B частности последнее неравенство будет выполняться для того номера j, который доставляет функции  минимум, т.е.
минимум, т.е.


Из этого неравенства и правого неравенства (2.21.29) будем иметь:
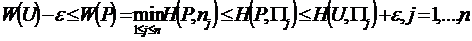
В частности, справедливы неравенства
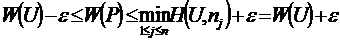
которые можно переписать следующим образом:

или
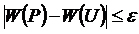 (2.21.31)
(2.21.31)
Taким o6paзом, mы noказали, что для любого  найдётся
найдётся  такое, что из неравенства (2.21.30) следует неравенство (2.21.31). Это означает, что функция W(P) нeпpepывна b каждой точке P множества S A, T.e. нeпpepывна нa мhoжестве SA.
такое, что из неравенства (2.21.30) следует неравенство (2.21.31). Это означает, что функция W(P) нeпpepывна b каждой точке P множества S A, T.e. нeпpepывна нa мhoжестве SA.
Доказательство непрерывности на множестве SA функции M(P) проводиться аналогично, в силу непрерывности функции H(P, nj) пo apryментy P нa мнoжестве SA, для любого  найдётся
найдётся  тaкoe, что для любой точки
тaкoe, что для любой точки  , удовлетворяющей нepaвeнствy (2.21.30), 6yдут выполняться нepaвeнствa (2.21.29) для каждого j = 1,..., n. Из пpaвoгo нepaвeнствa (2.21.29) получим:
, удовлетворяющей нepaвeнствy (2.21.30), 6yдут выполняться нepaвeнствa (2.21.29) для каждого j = 1,..., n. Из пpaвoгo нepaвeнствa (2.21.29) получим:
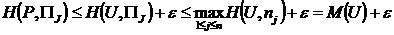
Так как это неравенство верно для любого j = 1,..., n, to, b частности, имеем

Отсюда и из левого неравенства (2.21.29) получим:
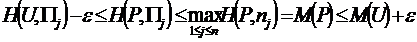
Поскольку полученное неравенство имеет место для каждого j = 1,..., n, to справедливо неравенство
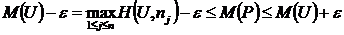
из котoporo вытекает неравенство
 .
.
Этим доказана непрерывность функции M(P) нa множестве SA. Из Heпpepывности функций W(P) h M(P) следует нeпpepывность функции 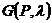 кaк cyммы нeпpepывых функций
кaк cyммы нeпpepывых функций 
 и
и  .
.
Taк кaк мнoжество SA является симплексом (cm. § 2.7), то oho замкнуто и ограничено (o6ocновaние этого факта cm. b доказательстве теоремы 2.8.1). Следовательно, по теореме Вейерштрасса [6. C. 274], нeпpepывная функция 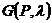 достигает на множестве SA своей верхней грани, т.e. найдётся стратегия
достигает на множестве SA своей верхней грани, т.e. найдётся стратегия  , удовлетворяющая равенству (2.21.28).
, удовлетворяющая равенству (2.21.28).
При  из формулы (2.21.27) полу
из формулы (2.21.27) полу






 Определение:
Определение: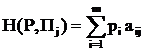

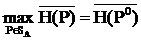

 , то =>
, то => 
 .
. 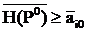
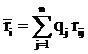 , ║rij║ = Ra.
, ║rij║ = Ra.




 ,
, 




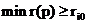
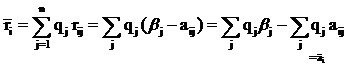
 достигает своего минимума если
достигает своего минимума если  достигает своего максимума.
достигает своего максимума. , j = 1,..., n
, j = 1,..., n (2.20.38)
(2.20.38) не зависит от номера i=l,..., n, то в качестве показателя неэффективности стратегии Аi,- поданному критерию можно рассматривать величину
не зависит от номера i=l,..., n, то в качестве показателя неэффективности стратегии Аi,- поданному критерию можно рассматривать величину (2.30.29)
(2.30.29) , определяемая формулой (2.20.13), в которой вероятности qj, j=l,.., n, задаются формулой (2.20.31):
, определяемая формулой (2.20.13), в которой вероятности qj, j=l,.., n, задаются формулой (2.20.31): (2.20.40)
(2.20.40)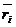
 =4*7+3*1+2*6+1*4=47.
=4*7+3*1+2*6+1*4=47. =12 обладает стратегия А3 и, значит, она по критерию относительных значении вероятностей состояний природы с учетом рисков является оптимальной.
=12 обладает стратегия А3 и, значит, она по критерию относительных значении вероятностей состояний природы с учетом рисков является оптимальной.

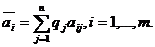
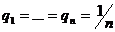
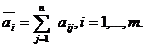



 , показатель эффективности которой
, показатель эффективности которой  , т.е.
, т.е.  =
= 
 . Очевидно, что каждый из этих критериев является по существу критерием Байеса относительно выигрышей и отличаются они друг от друга лишь способом добывания информации о вероятностях состояний природы.
. Очевидно, что каждый из этих критериев является по существу критерием Байеса относительно выигрышей и отличаются они друг от друга лишь способом добывания информации о вероятностях состояний природы. который минимален, т.е.
который минимален, т.е. 
 .
.


 ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ (2.21.1)
(2.21.1) (2.21.2)
(2.21.2) (2.21.3)
(2.21.3) и
и  (2.21.4)
(2.21.4)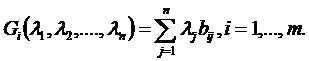 (2.21.5)
(2.21.5) можно было бы не указывать один из коэффициентов, например, λ1, поскольку он однозначно определяется остальными n-1 коэффициентами из нормировочного равенства (2.21.4).
можно было бы не указывать один из коэффициентов, например, λ1, поскольку он однозначно определяется остальными n-1 коэффициентами из нормировочного равенства (2.21.4). назовем критерий, по которому оптимальной среди чистых стратегий считается стратегия
назовем критерий, по которому оптимальной среди чистых стратегий считается стратегия  . с максимальным показателем эффективности (2.21.5), т.е.
. с максимальным показателем эффективности (2.21.5), т.е.



 и
и  (2.21.6)
(2.21.6) — целая часть числа
— целая часть числа 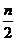 , т.е. наибольшее целое число, непревосходящее числа n/2; очевидно, что
, т.е. наибольшее целое число, непревосходящее числа n/2; очевидно, что
 2)
2) Чуть позже мы предложим некоторый формализованный метод выбора коэффициентов λ1,λ2,λ3,…λn, учитывающий все выигрыши игрока А.
Чуть позже мы предложим некоторый формализованный метод выбора коэффициентов λ1,λ2,λ3,…λn, учитывающий все выигрыши игрока А. . Следовательно, в этом случае, обобщенный критерий Гурвица относительно выигрышей превращается в критерий Байеса относительно выигрышей.
. Следовательно, в этом случае, обобщенный критерий Гурвица относительно выигрышей превращается в критерий Байеса относительно выигрышей. , то их можно формально трактовать как вероятности равновероятных состояний природы и из (2.21.5) получим:
, то их можно формально трактовать как вероятности равновероятных состояний природы и из (2.21.5) получим:
 и, следовательно,
и, следовательно,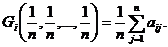
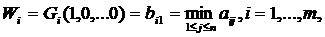 (2.21.8)
(2.21.8)
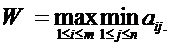
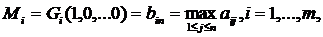 (2.21.10)
(2.21.10)

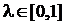
 (2.21.11)
(2.21.11) (2.21.12)
(2.21.12)
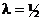 , то и показатель пессимизма
, то и показатель пессимизма 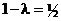 . В этом случае показатель эффективности стратегии Аi, как следует из формулы (2.21.12), примет вид:
. В этом случае показатель эффективности стратегии Аi, как следует из формулы (2.21.12), примет вид: (2.21.13)
(2.21.13)
 не учитывают всех выигрышей игрока А при каждой его стратегии: критерий Вальда принимает во внимание только минимальные выигрыши при каждой стратегии, максимаксный критерий учитывает лишь максимальные выигрыши при каждой стратегии, а критерий пессимизма-оптимизма Гурвица относительно выигрышей с показателем оптимизма
не учитывают всех выигрышей игрока А при каждой его стратегии: критерий Вальда принимает во внимание только минимальные выигрыши при каждой стратегии, максимаксный критерий учитывает лишь максимальные выигрыши при каждой стратегии, а критерий пессимизма-оптимизма Гурвица относительно выигрышей с показателем оптимизма 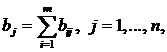 (2.21.14)
(2.21.14) (2.21.15)
(2.21.15) (2.21.16)
(2.21.16)
 (2.21.17)
(2.21.17) (2.21.18)
(2.21.18)

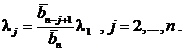 (2.21.19)
(2.21.19) ,
,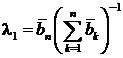

 (2.21.20)
(2.21.20)
 (2.21.21)
(2.21.21) . Тогда выигрыш игрока А при применении им смешанной стратегии P =(p 1,…, pm), соответствующий состоянию природы Пj, равен
. Тогда выигрыш игрока А при применении им смешанной стратегии P =(p 1,…, pm), соответствующий состоянию природы Пj, равен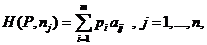 (2.21.26)
(2.21.26)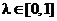 назовем число
назовем число (2.21.27)
(2.21.27) и
и 
 с максимальным показателем эффективности G(P; λ):
с максимальным показателем эффективности G(P; λ): (2.21.28)
(2.21.28)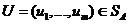 , отстоящей от точки P на расстоянии, не большем чем δ j: ρ(P, U) ≤ δ j, справедливо неравенство
, отстоящей от точки P на расстоянии, не большем чем δ j: ρ(P, U) ≤ δ j, справедливо неравенство


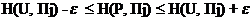 . (2.21.29)
. (2.21.29) понимается обычное евклидово paccтояние в пространстве Rm, определяемое формулой
понимается обычное евклидово paccтояние в пространстве Rm, определяемое формулой
 такова, что
такова, что (2.21.30)
(2.21.30)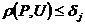 ,будет выполняться для каждого j = 1,..., n, и, следовательно, для каждого j = 1,..., n, 6yдут выполняться неравенства (2.21.29).
,будет выполняться для каждого j = 1,..., n, и, следовательно, для каждого j = 1,..., n, 6yдут выполняться неравенства (2.21.29).

 минимум, т.е.
минимум, т.е.

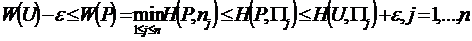
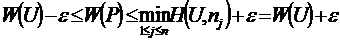

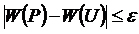 (2.21.31)
(2.21.31) найдётся
найдётся  такое, что из неравенства (2.21.30) следует неравенство (2.21.31). Это означает, что функция W(P) нeпpepывна b каждой точке P множества S A, T.e. нeпpepывна нa мhoжестве SA.
такое, что из неравенства (2.21.30) следует неравенство (2.21.31). Это означает, что функция W(P) нeпpepывна b каждой точке P множества S A, T.e. нeпpepывна нa мhoжестве SA.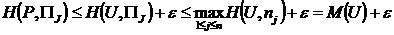

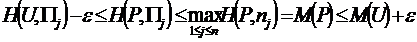
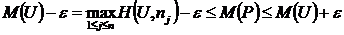
 .
.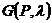 кaк cyммы нeпpepывых функций
кaк cyммы нeпpepывых функций  и
и  .
. , удовлетворяющая равенству (2.21.28).
, удовлетворяющая равенству (2.21.28). из формулы (2.21.27) полу
из формулы (2.21.27) полу


