Укажите все верные утверждения.

Укажите все верные утверждения.

Предмет теории игр – это

А) поиск оптимальных решений многокритериальной оптимизации;

Б) поиск мотивов принятия оптимальных решений;

В) поиск оптимальных решений в организационных системах;

Г) поиск оптимальных решений в условиях неопределенности;

Д) поиски и принятие решений в условиях конфликта;

Е) все утверждения от А) до Д) не верны.

 

2. Оптимальная стратегия игрока

А) есть функция нескольких переменных;

Б) всегда зависит от стратегий других игроков;

В) полностью определяет тип игрока;

Г) всегда Парето-оптимальна;

Д) всегда единственна;

Е) все утверждения от А) до Д) не верны.

Парето-оптимальное равновесие

А) редко совпадает с другими видами равновесий;

Б) никогда не совпадает с другими видами равновесий;

В) всегда единственное;

Г) никогда не бывает единственным;

Д) существует всегда;

Е) все утверждения от А) до Д) не верны.

Доминирующая стратегия

А) оптимальна при определенных стратегиях других игроков;

Б) всегда существует;

В) .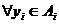

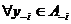
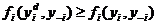Г) бывает неединственна;

Д) может быть равной 0;

Е) все утверждения от А) до Д) не верны.

Осторожная стратегия

А) ;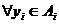

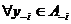
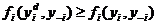Б) ,

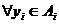
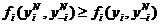В) ,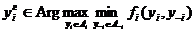

Г) все предыдущие утверждения не верны.

Равновесие Нэша

А) ;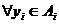

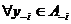
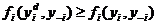Б) ,

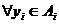
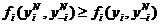В) ,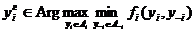

Г) все предыдущие утверждения не верны.

Обстановка игры для i-го агента.

А) ;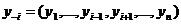

Б) ;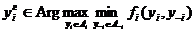

В) определяет его оптимальную стратегию;

Г) создается при его участии;

Д) определяет его доминирующую стратегию;

Е) все предыдущие утверждения не верны.

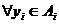
8. 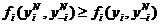- это

А) Парето-оптимальная стратегия;

Б) равновесие Нэша;

В) осторожная стратегия;

Г) минимаксная стратегия;

Д) равновесие Нэша;

Е) все утверждения от А) до Д) не верны.

В данной игре

благожелательность к игроку 2
неблагожелательность к игроку 2
	благожелательность к игроку 1	неблагожелательность к игроку 1

А) нет доминирующих стратегий;

Б) все стратегии - доминирующие;

В) все стратегии – осторожные;

Г) все равновесия – Парето-оптимальные;

Д) есть равновесие по Нэшу;

Е) все утверждения от А) до Д) не верны.

10. В игре: стратегии у_i = [0; 1]; выигрыши – .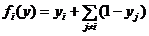

А) у_i = 0 – осторожная стратегия;

Б) у_i =0 – равновесие Нэша;

В) у_i =1 – равновесие в доминантных стратегиях;

Г) у_i =1/2 – Парето-оптимальное равновесие;

Д) у_i =1 – Парето-оптимальное равновесие;

Е) все утверждения от А) до Д) не верны.

 

Модуль 2. Тест 2 по дисциплине «Теория игр» Тема: Антагонистические игры.

Укажите все верные утверждения.

Антагонистическая игра

А) это игра с нулевой суммой;

Б) является конечной или бесконечной;

В) может быть матричной;

Г) всегда имеет решение;

Д) полностью задается платежной матрицей;

Е) все утверждения от А) до Д) не верны.

 

4. Оптимальная стратегия игрока в антагонистической игре

А) существует всегда;

Б) является осторожной стратегией;

В) является доминирующей стратегией;

Г) всегда приводит к Парето-оптимальному исходу;

Д) всегда единственна;

Е) все утверждения от А) до Д) не верны.

В игре с платежной матрицей

	1/2	5/6
	3/4	1/2

и смешанными стратегиями P=(3/8; 5/8) и Q=(1/4; 0; ¾)

 

А) выигрыш. Равный 1/2 достигается с вероятностью 1/8;

Б) максимальный выигрыш равен 1;

В) средний выигрыш равен 0.625;

Г) есть цена игры;

Д) P=(3/8; 5/8) и Q=(1/4; 0; ¾) – оптимальные стратегии;

Е) все предыдущие утверждения не верны.

Программа экзамена.

1. Классификация игр. Определение игры в нормальной форме.

2. Виды стратегий (осторожные, доминирующие, доминируемые, недоминируемые). Примеры.

3. Виды игровых равновесий.

4. Определение игры в развернутой форме

5. Переход от игры в развернутой форме к игре в нормальной форме.

6. Доминирование по Парето. Оптимальность по Парето. Пример.

7. Равновесие по Нэшу в чистых стратегиях. Теорема Нэша о существовании равновесия. Пример.

8. Смешанные стратегии. Равновесие по Нэшу в смешанных стратегиях. Теорема Нэша о существовании равновесия. Пример.

9. Разрешимость игры по доминированию (удаление доминируемых стратегий). Пример.

10. Игры с нулевой суммой. Чистые и смешанные стратегии. Теорема о минимаксе. Примеры.

11. Теорема фон Неймана о равновесии в антагонистических играх в смешанных стратегиях. Критерии и свойства оптимальных стратегий.

12. Игры с природой. Неопределенность и риск. Критерии Байеса, Лапласа, Гурвица.

13. Игры с природой. Критери, Вальда, Сэвиджа, миниминный, максимаксный.

14. Кооперативные игры. Коалиции. Характеристическая функция игры. Пример.

15. Дележ. Доминирование дележей. Пример.

16. С-ядро. Пример

15. Иерархические игры. Игры Г1, Г2, Г3. Примеры.

16. Иерархические игры. Равновесие по Штакельбергу. Пример.

16. Иерархические игры. Равновесие в осторожных стратегиях. Пример.

 

 

5. Список литературы и других информационных источников. [1]

Литература.

Основная:

1 Нейман Д., Моргенштерн О. Теория игр и экономическое поведение. – М.: Наука, 1970.

2 Воробьев Н.Н. Теория игр для экономистов и кибернетиков. М.Наука, 1985, 272С.

3 Данилов В.И. Лекции по теории игр. – М.: Российская экономическая школа, 2002.

4 Экономико-математическое моделирование. Учебник для студентов вузов. Под ред. И.Н. Дрогобыцкого., М.»Экзамен», 2004,- 800С.Оуэн Г. Теория игр. – М.: Мир, 1971.

5 Интриллигатор М. Математические методы оптимизации и экономическая теория. – М.: Прогресс, 1975.

6 В.И. Курбатов, Г.А. Угольницкий, Математические методы социальных

технологий, Москва, Вузовская книга, 1998.

Дополнительная:

7 ^*Гермейер Ю.Б. Игры с непротивоположными интересами. М.: Наука, 1976.

8 ^*Губко М.В., Новиков Д.А. Теория игр в управлении организационными системами. – М.: Синтег, 2002.

9 ^* Кукушкин Н.С., Морозов В.В. Теория неантагонистических игр. – М.: МГУ, 1984.

10 ^*Новиков Д.А., Чхартишвили А.Г. Рефлексивные игры. – М.: Синтег, 2003.

11 Новиков Д.А. Стимулирование в социально-экономических системах (базовые математические модели). – М.: ИПУ РАН, 1998.

12 ^*Лефевр В.А. Конфликтующие структуры. – М.: Советское радио, 1973.

13 А.А. Воронин, М.В. Губко, С.П. Мишин, Д.А. Новиков. Математические модели организаций. Москва, 2008. СИНТЕГ

 

Конспект лекций по дисциплине «Теория игр»

 

Тема 1. Лекция 1. История теории игр. Основные понятия теории игр. Классификация игр.

 

Теория игр – часть теории математических моделей принятия оптимальных решений (исследования операций), а именно, она моделирует ситуации принятия оптимальных решений в условиях конфликта.

История теории игр. В 1911 г. Э. Цермело описал теоретико-игровой подход к шахматной игре. В 1921г. Э. Борель начал систематическое изучение матричных игр. В 1928г. вышла работа Дж. Фон-Неймана «К теории стратегических игр», содержащая основные идеи современной теории игр. В 1943г. после публикации книги Дж. Фон-Неймана и О Моргенштерна «Теория игр и экономическое поведение» теория игр окончательно сформировалась как самостоятельная наука.

Смешанные стратегии

При построении нормальной формы игры по ее развернутой форме, множества стратегий развернутой игры превращаются во множества действий игры в нормальной форме. Зачастую действие игрока в игре в нормальной форме также называют стратегией. Это не совсем верно. Обычно термин «стратегия» имеет более широкий смысл и используется для обозначения плана, который каждый игрок составляет до начала игры. Этот план описывает все действия, которые игрок будет предпринимать во всех возможных игровых состояниях. Стратегия игроков даже в игре в нормальной форме может быть более сложной, чем просто выбор одного из элементов множества действий 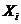(стратегия, состоящая в выборе действия из множества 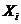, называется чистой стратегией).

Вспомним, что в играх в развернутой форме для тех ходов, которые делала природа, указывалась вероятность того или иного ее «хода». Аналогично и игроки могут не выбирать в каждой ситуации некоторое единственное действие, а выбирать одно из действий с некоторой вероятностью. Тогда выбор игрока будет описываться вероятностным распределением на множестве возможных в данной игровой ситуации действий, которое называется смешанной стратегией. Оказывается, что такое поведение в некоторых ситуациях может привести игрока к более выгодному распределению полезностей.

Определение 4: Смешанной стратегией 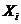i-гo игрока 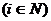для игры в нормальной форме называется распределение вероятности на множестве действий 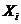с плотностью 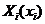, где .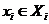

Определение 5: Вектор действий 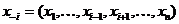всех игроков, кроме i-гo, называется обстановкой игры для i-го игрока .

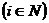Определение 6: Распределение вероятности (с плотностью 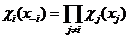) появления заданной обстановки при использовании игроками смешанных стратегий 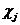называется обстановкой в смешанных стратегиях для i-гo игрока, .

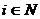Ожидаемый выигрыш игроков при использовании ими смешанных стратегий будет вычисляться как математическое ожидание их функции выигрыша. Для дискретных игр

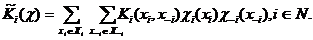
Смешанная стратегия для непрерывных игр представляет собой вероятностную меру на множестве чистых стратегий игрока. Ожидаемая полезность игроков при использовании ими смешанных стратегий будет интегралом функции полезности по декартову произведению этих вероятностных мер.

Дискретную игру, в которой игроки используют смешанные стратегии, можно привести к непрерывной игре, в которой игроки используют только чистые стратегии. Это достигается путем замены множества чистых стратегий игрока на множество его смешанных стратегий, а функции выигрыша – ее математическим ожиданием.

Тогда можно исследовать свойства новой игры в предположении, что игроки используют только чистые стратегии. Это, однако, не всегда бывает удобным, так как такой переход приводит к замене более простой, дискретной игры, более сложной – непрерывной

Приведем несколько свойств смешанных стратегий в дискретных играх.

Лемма 1. Ожидаемая полезность дискретной игры – непрерывная функция смешанных стратегий.

Теорема 2. Для произвольной обстановки в смешанных стратегиях найдется чистая стратегия, являющаяся «наилучшим ответом» на данную обстановку, то есть

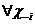
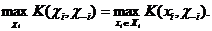
Более того, любая смешанная стратегия ,которая содержит с ненулевой вероятностью чистую стратегию, не являющуюся лучшим ответом на обстановку 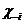,не будет и сама лучшим ответом на обстановку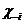

Доказательство. Множество смешанных стратегий - это компакт, в котором содержатся и чистые стратегии. Для игрока i зафиксируем обстановку в смешанных стратегиях 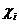. Тогда ожидаемый выигрыш игрока i будет функцией только его смешанной стратегии 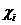. Очевидно, существует смешанная стратегия 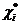, при использовании которой ожидаемый выигрыш достигает максимума (значком 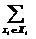обозначается суммирование по всем элементам множества ).

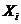Для стратегии 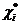ожидаемый выигрыш есть

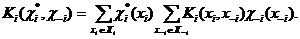(2)

Так как 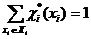то 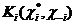представляет собой взвешенную с весами 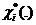сумму величин

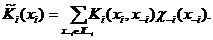(3)

Взвешенная сумма (3) не может превышать своего максимального слагаемого, то есть существует чистая стратегия 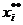для которой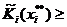 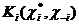. Но в правой части этого неравенства стоит максимальный ожидаемый выигрыш, возможный при использовании смешанных стратегий. Значит, неравенство можно заменить равенством, а это, в свою очередь, значит, что максимальный ожидаемый выигрыш достигается на не которой чистой стратегии. Кроме того, если любой не максимальный элемент (3) входит в сумму (2) с ненулевым весом, то ожидаемая полезность будет строго меньше максимально возможной и смешанная стратегия не будет наилучшим ответом на обстановку .

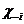Смешанные стратегии – довольно хрупкая конструкция. Их использование в ряде практических задач неоднократно подвергалось критике. Один из аргументов против использования смешанных стратегий таков: «Применение смешанных стратегий подходит только для игр с большим числом повторений. Рассмотрим игру, которая должна быть сыграна лишь один раз. При использовании смешанных стратегий игрок должен выбирать свое решение на основании реализации случайного процесса, задаваемого распределением вероятности его смешанной стратегии. Однако эта реализация может дать стратегию, настолько «экзотическую», что ее применение в единичной игре будет малоэффективно, несмотря на теоретические обоснования эффективности такой смешанной стратегии в смысле среднего выигрыша на протяжении многих игр».

Поэтому, когда возможно, особенно при моделировании реальных систем, следует использовать только чистые стратегии.

 

Определение.

Стратегия 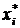игрока 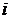в игре (1) называется доминирующей (абсолютно оптимальной), если

.

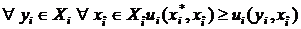Обозначим через 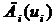множество всех доминирующих стратегий i-го игрока.

Определение.

Исход 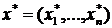называется равновесием в доминирующих стратегиях, если 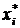является доминирующей стратегией i-го игрока при всех .

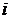Лемма 1.

Пусть для любого 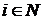множество 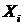компактно, а функция 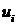непрерывна. Тогда множество 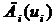недоминируемых стратегий i-го игрока не пусто.

В противоположность этому, доминирующие стратегии могут не существовать даже в весьма простых играх. В самом деле, доминирующая стратегия должна одновременно быть решением зада максимизации

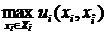
При всех значениях параметра 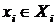; в общем случае не приходится ожидать, что такое решение существует

Определение.

Стратегии i-го игрока 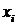и 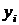называются эквивалентными, если они не различимы с его точки зрения:

.

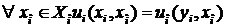Лемма 2.

Пусть в игре (1) множество недоминируемых стратегий i-го игрока не пусто: 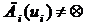, множества стратегий 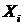компактны, функции выигрыша 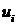непрерывны, .

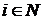Тогда следующие утверждения эквивалентны:

– существует доминирующая стратегия i-го игрока: ;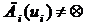

– все стратегии в множестве 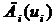эквивалентны.

 

…..если у игрока есть хотя бы одна доминирующая стратегия, то все доминирующие стратегии эквивалентны и совпадают с его недоминируемыми стратегиями. В этом случае будем считать, что если игрок использует одну из них (при некооперативном поведении, то есть действуя изолированно от других игроков). С другой стороны, если у i-го игрока нет доминирующей стратегии (наиболее частый случай), то его недоминируемые стратегии неэквивалентны, поэтому его некооперативное поведение не может быть определенно однозначно. Требуется дополнительные предположения об информации, которой располагают игроки (в частности, о функциях выигрыша).

Равновесие Нэша. Гораздо чаще, чем РДС, существует равновесие Нэша (РН). Джон Нэш, американский математик, в начале 50-х годов XX века предложил следующее: устойчивым исходом взаимодействия агентов можно считать такой вектор их действий, от которого в одиночку никому из них не выгодно отклоняться. Это значит, что ни один из агентов, в одиночку меняя свою стратегию на другую, не может увеличить свой выигрыш при условии, что остальные своих стратегий не меняют.

Формальное определение равновесия Нэша 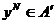таково:

(5) ,

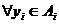
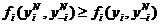то есть для любого агента и для любого допустимого его действия выбор им равновесного по Нэшу действия дает ему выигрыш не меньший, чем при выборе любого другого действия при условии, что остальные игроки играют равновесные по Нэшу стратегии.

Отличие между изложенными подходами (РДС и равновесием Нэша) заключается в том, что в формулировке равновесия в доминантных стратегиях (3) фигурирует произвольная обстановка, то есть доминантная стратегия – наилучшая при любой обстановке. А стратегия по Нэшу – наилучшая при «нэшевской» обстановке (см. (5)).

Равновесие Нэша хорошо тем, что в большинстве моделей оно существует. Одним из его недостатков является то, что оно не всегда единственно. Ведь если есть два равновесия, то как предсказать, в каком из них окажутся агенты. Нужны дополнительные предположения.

Кроме того, равновесие по Нэшу не устойчиво к отклонению двух и более игроков. По определению одному агенту не выгодно отклоняться, но это не значит, что если два агента договорились и одновременно отклонились от равновесной ситуации, то они не смогут оба выиграть. То есть равновесие Нэша – существенно некооперативная концепция равновесия.

Пример 2.11. Возьмем Пример 2.9 и найдем для него равновесие Нэша игры агентов, выбрав l ₀ = 5, r₁ = 1, r₂ = 2. Для этого продифференцируем целевую функцию каждого агента по его действию, приравняем производную нулю, и решим систему уравнений. Получим равновесные действия агентов: 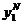= 15/13, 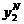= 20/13. ·

Пример 2.12. Пусть целевая функция i -го агента f_i (y, r_i) представляет собой разность между доходом h_i (y) от совместной деятельности и затратами c_i (y, r_i), где r_i – параметр эффективности (тип) агента, то есть

(6) f_i (y, r_i) = h_i (y) – c_i (y, r_i), i Î N.

Выберем следующий вид функций дохода и затрат:

(7) h_i (y) = g_i l Y, i Î N,

(8) c_i (y, r_i) = 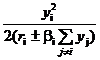, i Î N,

где Y = 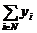, 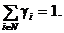Для случая, когда в знаменателе выражения (8) стоит знак «–», предполагается, что .

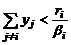Содержательно набор агентов может интерпретироваться как некоторая фирма, подразделения которой (агенты) производят однородную продукцию, реализуемую на рынке по цене l. Суммарный доход l Y распределяется между агентами в соответствии с фиксированными долями {g _i }. Затраты агента возрастают по его действиям, а эффективность деятельности (знаменатель выражения (8)) определяется типом агента. Взаимодействие агентов моделируется зависимостью затрат (эффективности деятельности) каждого из них от действий всех (других) агентов. Знак «+» в знаменателе выражения (8) соответствует эффективному взаимодействию агентов (убыванию затрат на масштаб) – чем большие действия выбирают другие агенты, тем меньше затраты (выше эффективность деятельности) рассматриваемого агента, что на практике может соответствовать снижению удельных постоянных издержек, обмену опытом, технологиями и т.д. Знак «-» в знаменателе выражения (8) соответствует неэффективному взаимодействию агентов (возрастанию затрат на масштаб) – чем большие действия выбирают другие агенты, тем больше затраты (ниже эффективность деятельности) рассматриваемого агента, что на практике может соответствовать нехватке основных фондов, ограничениям на побочные показатели (например, загрязнение окружающей среды) и т.д. Коэффициенты {b _i ³ 0 } отражают степень взаимозависимости агентов.

Пусть рыночная цена l известна всем агентам. Тогда, дифференцируя целевые функции агентов, приравнивая производные нулю и складывая получившиеся при этом выражения

y_i = g _i l(r_i ± b _i 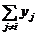), i Î N,

получим следующую зависимость суммарных действий от параметра l:

Y (l) = .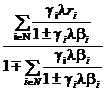

Пусть n = 2, g _i = b _i = 1/2, i = 1, 2, тогда суммарное действие и равновесные по Нэшу действия агентов равны, соответственно:

(9) Y (l) = 2 l R / (4 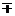l),

(10) y^*_i (l) = 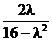(4 r_i 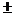l r_-i), i = 1, 2. ·

Эффективность по Парето. Помимо перечисленных выше концепций равновесия (которые далеко не исчерпывают имеющегося на сегодняшний день разнообразия определений равновесия), необходимо ввести понятие эффективности по Парето (названное в честь предложившего это понятие итальянского экономиста В. Парето). Вектор действий агентов 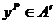(точка Парето), принадлежащий множеству A' допустимых векторов действий, будет эффективным по Парето, если для любого другого вектора действий найдется агент такой, что значение его целевой функции будет строго меньше, чем в точке Парето:

.

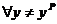
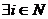
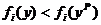Т.е. точка Парето – такая точка, отклоняясь от которой, мы не можем одновременно увеличить значения целевых функций всех игроков. Концепция эффективности по Парето хороша тем, что позволяет говорить, что, если мы можем увеличить выигрыши всех без исключения агентов, то это надо делать.

Один из ключевых вопросов, исследованием которого занимается теория игр, заключается в том, как соотносятся все вышеперечисленные концепции равновесия (максиминное равновесие, РДС и равновесие Нэша) с эффективностью по Парето, т.к. хочется, чтобы результат, приносящий индивидуальный оптимум, был бы еще эффективным для общества (коллектива агентов) в целом. Оказывается, что эффективность по Парето, к сожалению, никак не соотносится ни с одной из трех концепций решения игры (равновесия), изложенных выше.

Пример 2.13. Рассмотрим Пример 2.10, в котором обозначим b _j = 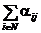, b ₀ = 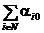. Тогда суммарный выигрыш агентов равен

(11) S (y) = b ₀ + .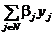

Доставляющее максимум выражению (11) и эффективное по Парето действие i -го агента есть:

(12) 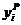= Sign(b _i), i Î N.

Если " i Î N Sign(a_{i i} ) = Sign(b_i), то РДС является эффективным по Парето. Если $ i Î N:Sign(a _ii) ¹Sign(b _i), то требуется согласование интересов агентов. ·

Пример 2.14. Рассмотрим хрестоматийный пример с конкретными целевыми функциями. Пусть каждый игрок выбирает действия из отрезка A_i = [ 0; 1 ]. Выигрыш i -го агента – 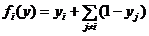. Исследуем, существует ли равновесие в доминантных стратегиях или равновесие по Нэшу.

Если внимательно посмотреть на целевую функцию, то видно, что i -му агенту выгодно, максимизируя свою целевую функцию, выбирать максимальное значение своего действия независимо от того, что делают остальные (производная по действию i -го агента строго положительна независимо от обстановки). Значит, каждый агент будет выбирать максимальное значение своего действия, т.е. для него существует доминантная стратегия. Чтобы не выбрали остальные, он, увеличивая свое действие, выигрывает, а больше единицы он выбрать не может, значит, 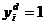, i Î N.

Вычислим выигрыш каждого агента от равновесия в доминантных стратегиях. Если все выбрали по единице, то каждый получил выигрыш, равный единице: 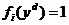, i Î N.

Рассчитаем теперь один из векторов действий, эффективных по Парето (вычислив, например, максимум суммы целевых функций всех агентов). Это – вектор нулевых действий: 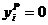, i Î N. Если все агенты выбирают нулевые действия, то выигрыш i -го агента равен 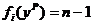, i Î N, и нельзя увеличить выигрыш одновременно всех агентов. Если мы хотим увеличить выигрыш i -го агента и начинаем увеличивать его действие, то тем самым уменьшаем выигрыши остальных, потому что это действие входит с минусом в целевые функции других агентов.

Если играют три или более агентов, то, выбирая действия, эффективные по Парето, они получают строго больше, чем играя доминантные стратегии, так как 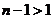при n ³ 3.

Спрашивается, будет ли точка Парето точкой равновесия Нэша (ведь любое РДС является равновесием Нэша), то есть рациональной с точки зрения индивидуального поведения. Если кто-то из игроков выберет ненулевую стратегию, он выиграет. Поэтому он увеличит свое действие до единицы, остальные поступают аналогично, и все «скатывается» к ситуации равновесия в доминантных стратегиях, которая никому не выгодна, но устойчива. ·

Другим хрестоматийным примером неэффективности по Парето равновесия Нэша является следующий. Представим себе толпу зрителей, наблюдающих за уличным театральным представлением. У каждого зрителя есть два действия – стоять «как обычно» или встать «на цыпочки». Ситуация, когда все стоят «как обычно» не устойчива – один встает «на цыпочки», чтобы лучше видеть, но загораживает обзор другим. В результате все страдают, стоя «на цыпочках». Получили неэффективную по Парето (всем неудобно), но устойчивую по Нэшу ситуацию игры (если все стоят «на цыпочках», то отдельный зритель, встав «как обычно», ничего не увидит).

Рассмотренные примеры иллюстрирует, что устойчивость относительно индивидуальных отклонений никак не связана с эффективностью по Парето. Решить эту проблему можно следующим образом: если разыгрывается повторяющаяся игра, и игроки договариваются наказывать того, кто отклоняется от коллективного оптимума, т.е. равновесия по Парето, то оказывается, что, если наказание достаточно сильно, то каждый будет играть индивидуально устойчиво ту стратегию, которая выгодна для всех.

Другой вариант, как можно достичь «коллективного оптимума». Мы, описывая взаимодействие агентов, которые равноправны, принимаем решение назначить над ними «начальника», который будет ответственен за то, чтобы они не отклонялись от «коллективного оптимума», не пытались локально увеличить свой выигрыш, а выбирали равновесие, эффективное по Парето. Т.е. функция «начальника» – предотвратить отклонения агентов от оптимума по Парето. Можно даже рассчитать, сколько агенты могут выделить на содержание такого начальника (как разность между тем, что они получают в сумме в точке Парето и тем, что они имеют при равновесии в доминантных стратегиях). Это – одно из теоретико-игровых обоснований возникновения иерархий.

Итак, выше описана игра в нормальной форме, где выигрыш каждого агента зависит от действий всех, и все агенты принимают решения одновременно.

Теорема фон Неймана.

Пусть задана антагонистическая игра с платежной матрицей A (m, n) = (| a_ij |)

Определение. Смешанной стратегией игрока А называется дискретная случайная величина, принимающая значения 1,2,3,…m с определенной вероятностью;. смешанной стратегией игрока В называется дискретная случайная величина, принимающая значения 1,2,3,… n с определенной вероятностью.

					m
P1	P2				pm

P = (p₁, p₂ … p_m), p_i ≥ 0, ∑ p_i = 1. Q = (q₁, q₂ … q_n) (аналогично для Q).

Чистые стратегии игроков являются частными случаями смешанных, при этом

А1=(1,0,0,……0), А2=(0,1,0,……0) ….. Аm=(0,0,….0,1);

В1=(1,0,0,……0), В2=(0,1,0,……0) ….. Вn=(0,0,….0,1);

Тогда смешанные стратегии можно представить в виде

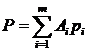, Ai - базисные векторы

 

Проанализируем структуру множества смешанных стратегий. Пусть у игрока А есть две чистые стратегии.

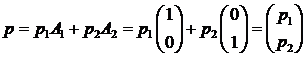- это множество называется одномерным симплексом.

 

 

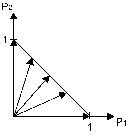
Для трех чистых стратегий имеем 2-мерный симплекс смешанных стратегий – треугольник с вершинами (1,0,0), (0,1,0), (0,0,1) (концы векторов P принадлежат треугольнику) и т.д.

 

 

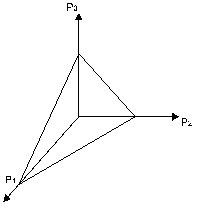
Определение. Пара (P, Q) – образует исход игры (или игровую ситуацию). В которой выигрыш игрока A, равный a_ij, достигается с вероятностью p_iq_j. H(P,Q) есть математическое ожидание выигрыша (средний выигрыш) при избранных стратегиях игроков 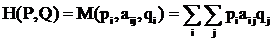- средний выигрыш A (проигрыш B) при (P,Q). В матричном виде: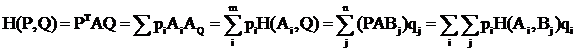

 

Пример. Пусть задана платежная матрица и стратегии игроков:

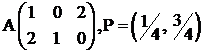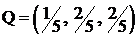, . Считаем векторы P, Q столбцами.

 

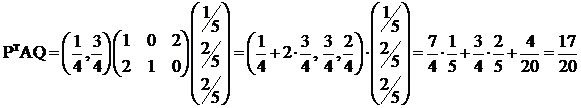
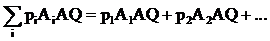
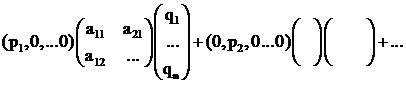
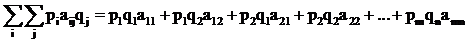
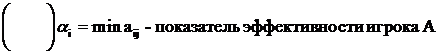
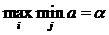- нижняя цена игры.

 

Определение. 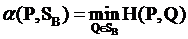- показатель эффективности стратегии P игрока A относительно смешанной стратегии Q игрока B. (S_B - множество смешанных стратегий игрока B.)

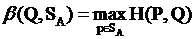- показатель неэффективности стратегии Q игрока B.

 

Теорема. Показатели α и β достижимы.Т.е.

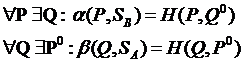
Доказательство:

Рассмотрим функцию α(P,S_B). Для 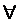фиксированной стратегии P H(P,Q) - есть функция одной векторной переменной Q на ограниченном замкнутом контуре.

 

Ограниченность:

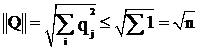, ∑q_i = 1, q_i≥ 0

Замкнутость.

Вспомним, что множество называется замкнутым, если оно содержит все свои предельные точки

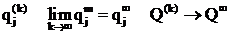. Если каждый элемент сходящейся числовой последовательности неотрицателен, то и ее предел (очевидно) также неотрицателен, т.е. 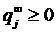Далее: . Это доказывает, что симплекс – замкнутое множество.

 

Теорема.

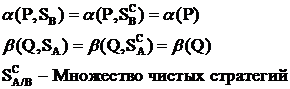
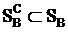- множество чистых стратегий является подмножеством смешанных стратегий.

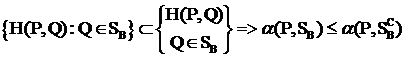
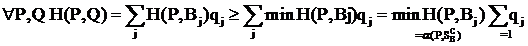
Верно для H(P, Q⁰) = α(P, S_B)

 

Определение. Нижней ценой игры в смешанных стратегиях называется величина:

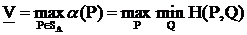
Верхней ценой игры в смешанных стратегиях называется величина:

 

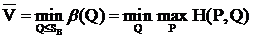
Теорема.

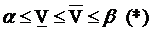где α, β - цены игры в чистых стратегиях.

Доказательство:

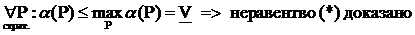
Докажем, что 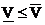: Для произвольных стратегий P и Q имеем:

 

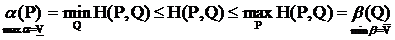
Определение. Если 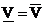, то игра имеет цену в смешанных стратегиях => Максиминная и минимаксная стратеги