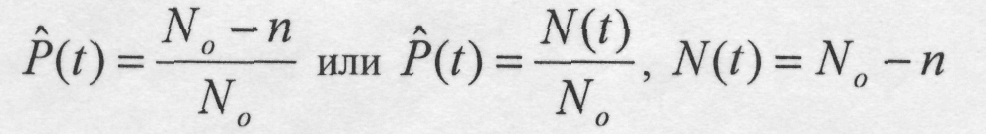Отказы предельного состояния вызывают вывод из эксплуатации объекта.
Наработка на такой отказ называется ресурсом, а предельное состояние оговаривается в технической документации.
Предельное состояние у аналогичных машин наступает через разную наработку (t) (для одной через t1, для другой через t2, для третьей через t3 и т.д.).
Наработки t1, t2, t3... рассматривают как случайные величины из-за сложности или невозможности их определить в аналитической форме.
Это объясняется множеством факторов, влияющих по-разному в каждом конкретном случае.
Для решения инженерных задач требуется знать среднюю наработку (средний ресурс) и как группируются частные ресурсы около среднего.
Поэтому возникает необходимость в знании закона распределения наработок на предельное состояние (распределение отказов).
Закон распределения случайных величин -это соотношение, устанавливающее связь между возможными значениями случайной величины / и соответствующими им:
• плотностями вероятности —f(t);
• функциями распределения - F(t);
• вероятностями (отсутствие отказов) - P(t);
• интенсивностью (отказов) -λ(t).
Каждая из этих зависимостей однозначно определяет закон распределения (см. рис. 4.2).

Вид закона распределения случайных наработок t до предельного состояния зависят от причин возникновения отказов. Для изучения надёжности объектов применяют разные законы распределения разработок до отказов.
| Закон распределения
| Плотность распределения
|
|
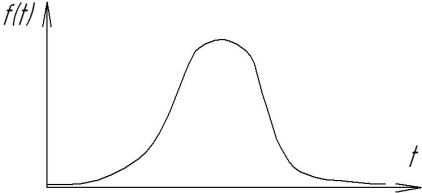
| Нормальное
| 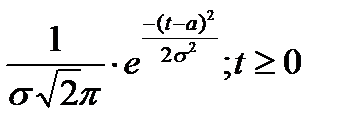
| 
|
| Экспоненциальное
| 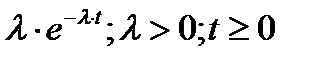
| 
|
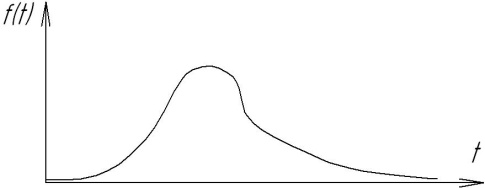
| Логарифмическое
| 
| 
|
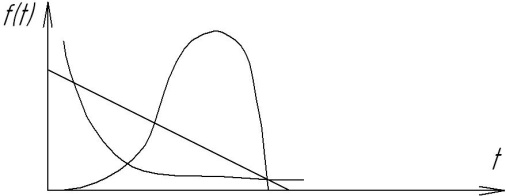
| Вейбулла
| 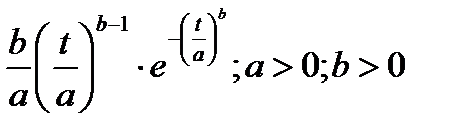
| 
|
Например, выход из строя элементов конструкций из-за износов хорошо согласуется с так называемым нормальным законом распределения; из-за превышения предельных напряжений - экспоненциальным законом; из-за старения материала - законом Вейбулла-Гнеденко и т.д.
Каждый из законов обладает определенными свойствами, использование которых позволяет предвидеть отказы элементов, принимать заранее необходимые меры, а в целом прогнозировать возникновение отказов.
Важное значение в теории надежности объектов, имеющих механическую основу, а, следовательно, и машин, имеет нормальный закон распределения (см. рис. 4.3 ).
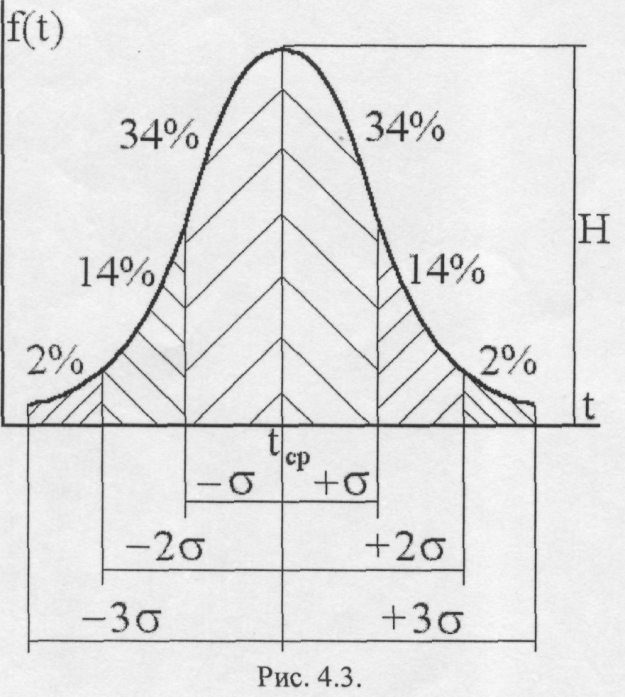
Кривая плотности вероятности описывается уравнением:
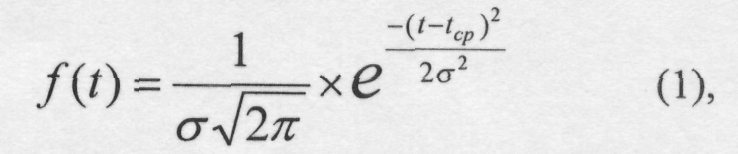
где t и tср – текущая и средняя (математическое ожидание) наработки;
е – основание натуральных логарифмов;
σ – среднее квадратичное отклонение.
Этот закон имеет следующие свойства:
1. Во-первых, абсцисса высоты Н, определяемой формулой 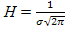 , соответствует средней наработке tcp, а суммы плотностей вероятностей слева и справа от tcp равны 0,5 (34+14+2=50%).
, соответствует средней наработке tcp, а суммы плотностей вероятностей слева и справа от tcp равны 0,5 (34+14+2=50%).
2. Во-вторых, участок абсциссы под всей кривой с точностью до 1% равен 6 а, а каждая а, отложенная от tcp, охватывает плотности, суммарно равные величинам, приведенным на графике.
Первоеиз приведенных свойств показывает, что до среднего ресурса и после него выходит из строя по 50% изделий. Затем чем больше среднее квадратичное отклонение, тем меньше высоты Н, поэтому тем более точной является кривая f(t) и при меньших наработках t начинают отказывать элементы конструкции.
Второе из указанных свойств приводит к тому, что tcp>3σ, а потому коэффициент вариации  .
.
Кроме того, зная только tcp и σ, можно построить всю кривую. Для этого рассмотрим не плотность вероятностей f(t), а функцию распределения F(t):

Средний ресурс tcp соответствует F(tcp)=0,5 по первому свойству закона.
Вероятность отсутствия отказа на промежутке от 0 до t находится по соотношению:
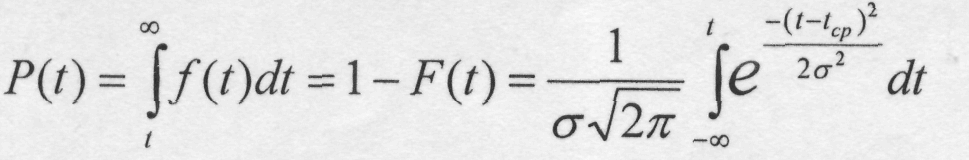
Переместим ось ординат на точку абсциссы t=tcp, т.е. условно примем tcp=0 (центрирование) и положим σ=1 (нормирование). Для этого случая уравнение (2) примет вид:
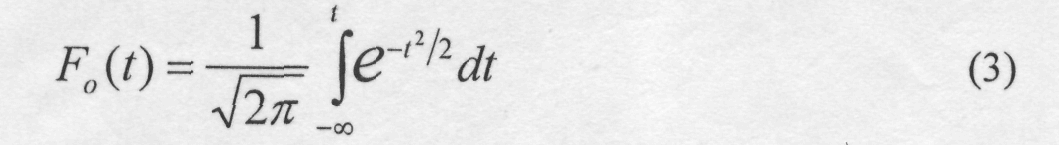
Из уравнений (2) и (3) получаем:
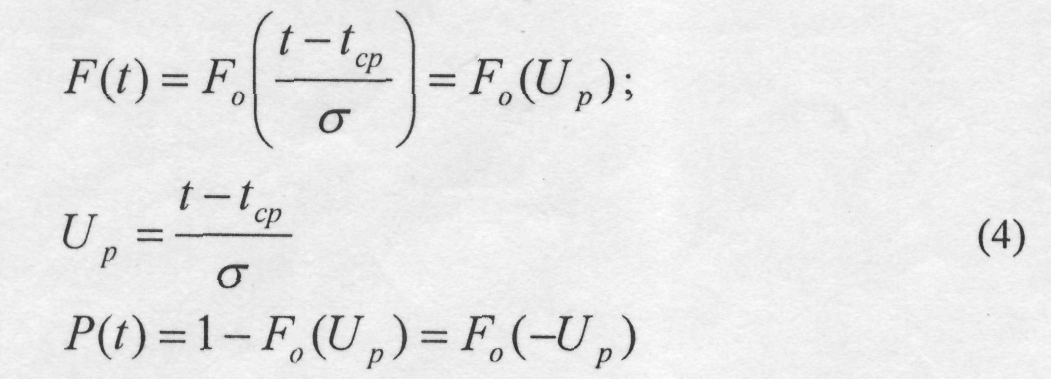
Квантилем Up нормального распределения, отвечающей вероятности Р, называют число, удовлетворяющее уравнению:

Значения квантилей приведены в таблицах. Применение квантилей позволяет по данным tcp и а построить кривые F(t) и P(t). Для этого преобразуем соотношение (4) и учтем, что нормальный закон обладает симметрией:

Для использования выражения (5) надо задавать поочередно Pj(t), по таблице определять UPj и затем выявлять tj, соответствующее Pj(t).
При экспоненциальном законе распределения плотности вероятностей определяются формулой:

Этот закон обладает следующими свойствами:
• до наступления среднего ресурса tcp выходит из строя 63%, и после его наступления tcp - 37% всех элементов;
• средняя наработка равна среднему квадратичному отклонению а, т.е. tcp=a, следовательно, коэффициент вариации V=l;
• отсутствует последствие, т.е. вероятность отказа не зависит от времени предшествующей работы.
Для пояснения последнего свойства предположим, что листы рессоры машины ломаются от удара определенной силы колеса о неровности дороги. Тогда не имеет значения, произошел ли такой удар на первых или последующих часах наработки машины, результат будет один и тот же.
Однако бывает, что разрушающие усилия зависят, конечно, от старения металла рессоры, а поэтому имеет место комбинация нескольких законов распределения, например Вейбула-Гнеденко и экспоненциального.
Функция распределения отказов элементов при экспоненциальном законе распределения определяется формулой:
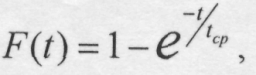
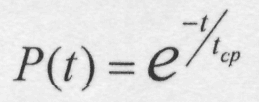 а вероятность того, что отказа не произойдет:
а вероятность того, что отказа не произойдет:
- эту формулу широко используют в теории надежности.
Рассмотрим использование распределений наработок для определения показателей безотказности (см. рис.4.4 ).
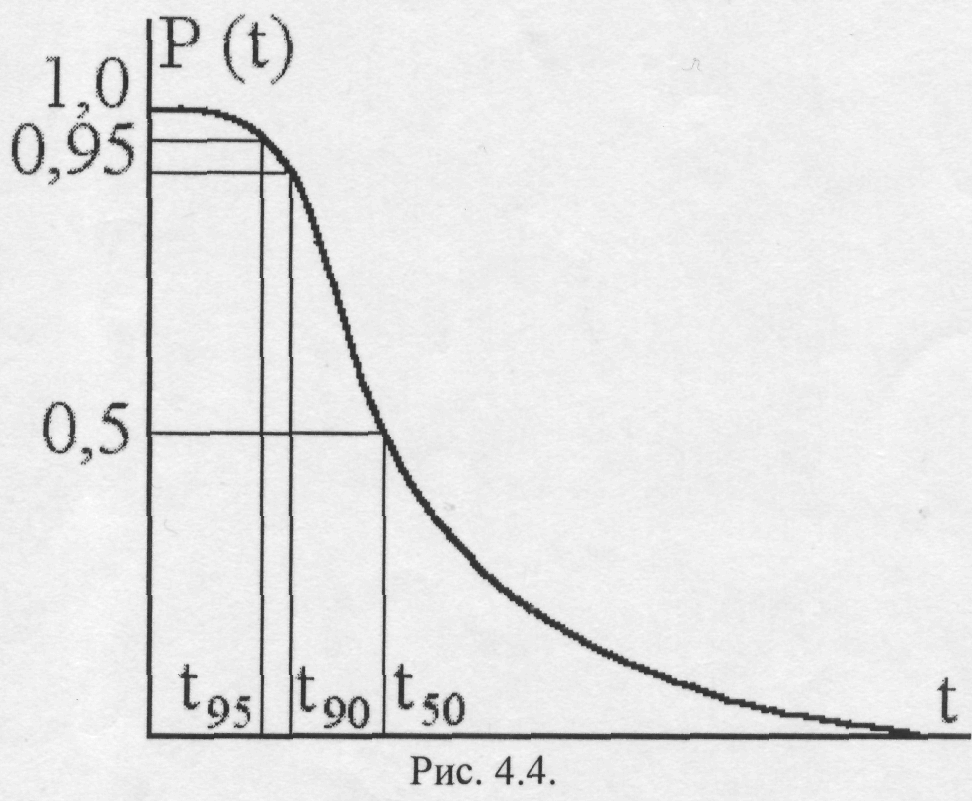
Вероятность безотказной работы P(t) - это вероятность того, что за данную наработку от 0 до t в данных условиях эксплуатации не произойдет ни одного отказа.
Приближенно P(t) определяют по формуле по общему числу объектов N0, находящихся под наблюдением (выборка), числу отказавших объектов п за наработку от 0 до t, числу работоспособных объектов N(t) при наработке t:
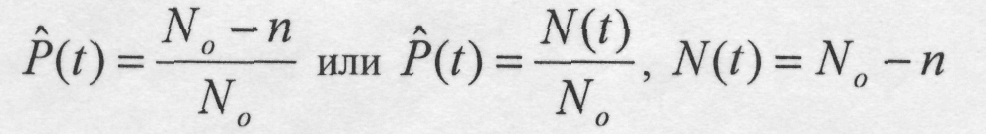
График вероятности безотказной работы позволяет применительно к отдельно взятому элементу конструкции предвидеть и численно оценить возможность отказа на той или иной его наработке.
Применительно же к достаточно большому парку машин вероятность P(t) позволяет определить, какая доля одновременно включенных в эксплуатацию объектов не будет иметь отказы за данную наработку 0-t.
Кроме того, график вероятности безотказной работы позволяет выявить так называемый гамма-процентный ресурс, т.е. ресурс, который имеет или превышает в среднем обусловленный процент элементов.
По этому графику можно рассчитать средний ресурс.
Таким образом, вероятность безотказной работы характеризует безотказность элементов при рассмотрении ее за всю наработку с начала эксплуатации.






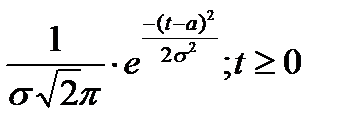

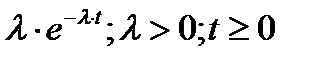



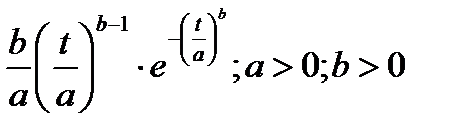


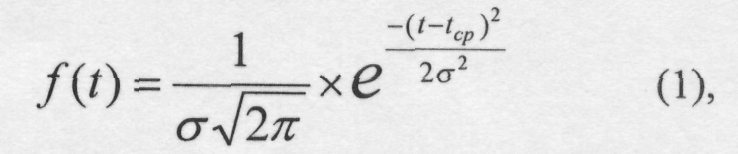
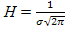 , соответствует средней наработке tcp, а суммы плотностей вероятностей слева и справа от tcp равны 0,5 (34+14+2=50%).
, соответствует средней наработке tcp, а суммы плотностей вероятностей слева и справа от tcp равны 0,5 (34+14+2=50%). .
.
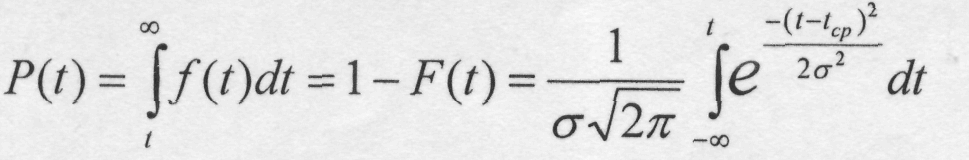
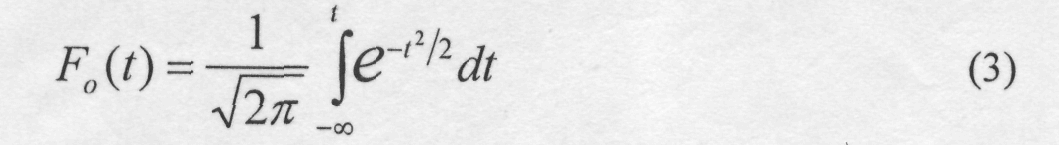
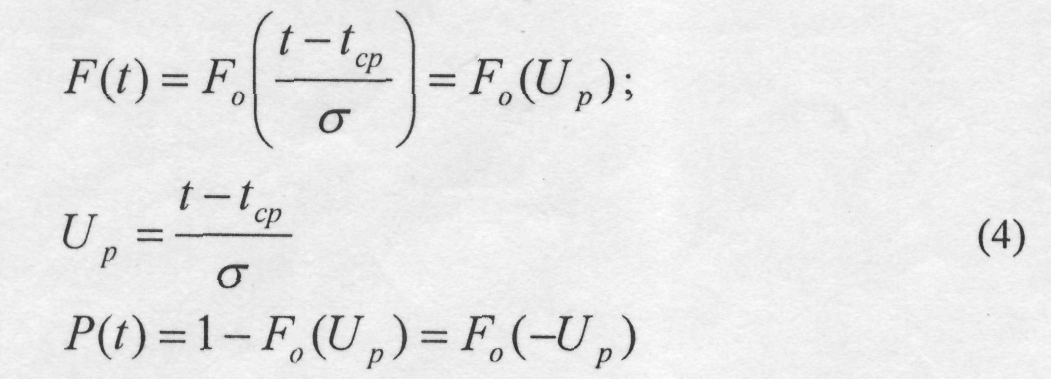



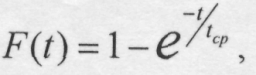
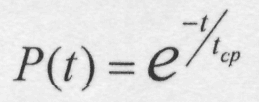 а вероятность того, что отказа не произойдет:
а вероятность того, что отказа не произойдет: