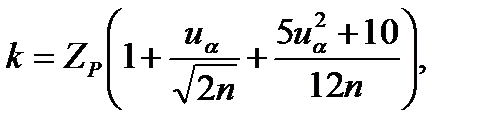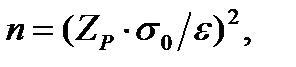Нормальный закон распределения наиболее часто используется для оценки надежности при постоянном отказе.
Плотность вероятности нормального распределения задана уравнением
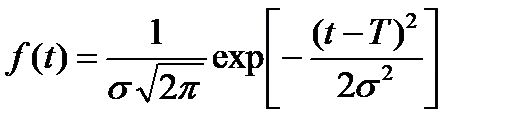
Т и σ - параметры закона (закон двухпараметрический).
Т - средняя наработка на отказ
σ - среднеквадратическое отклонение времени безотказной работы.
Так как при нормальном распределении случайная величина может принимать значения - ∞ до +∞, а время безотказной работы может быть только положительным, то нужно рассматривать усеченное нормальное распределение с плотностью

где с - нормирующий множитель, который определяется из выражения
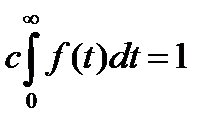
и равен 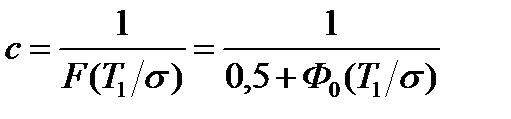
где  - табулированная интегральная функция нормального распределения;
- табулированная интегральная функция нормального распределения;
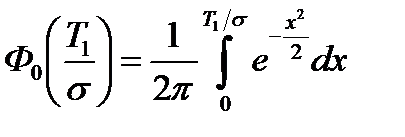 - нормированная функция Лапласа.
- нормированная функция Лапласа.
Средняя наработка до отказа и параметр Т1 усеченного нормального распределения связаны зависимостью
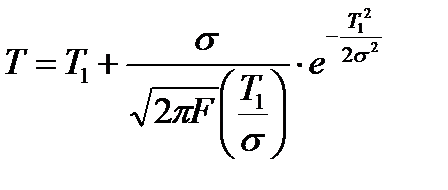
При  коэффициент
коэффициент  и усеченное нормальное распределение достаточно точно аппроксимируется обычным нормальным законом.
и усеченное нормальное распределение достаточно точно аппроксимируется обычным нормальным законом.
При испытании выборки объемом n изделий с наработкой t1, t2, … tn параметры T и σ оцениваются из формулы
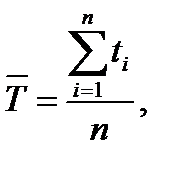

Доверительные границы средней наработки до отказа определяются по уравнениям

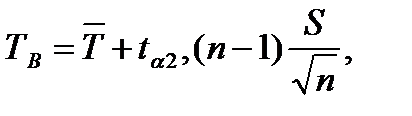
где 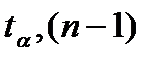 - квантиль распределения Стьюдента для вероятности α или уровня значимости β = 1 – α и числа степеней свободы f =n – 1.
- квантиль распределения Стьюдента для вероятности α или уровня значимости β = 1 – α и числа степеней свободы f =n – 1.
В случав двухстороннего определения доверительных границ (вспомнив, что α = α1 + α2 – 1)
α1 = α2 =(α + 1)/2, при этом уровни значимости β1 = β2 = (1 – α)/2.
Для разных партий величина Sn =[S] будет различной.
Рассматривая Sn как случайную величину с нормальным распределением мочено указать доверительные интервалы для равенства σ= Sn.
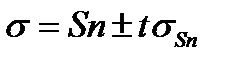
t - коэффициент доверительной вероятности, определяемый для распределения Стьюдента;
σSn – среднеквадратичное отклонение величины Sn.
σSn приближенно определяют из формулы 
Доверительные границы среднеквадратичного отклонения определяются как:
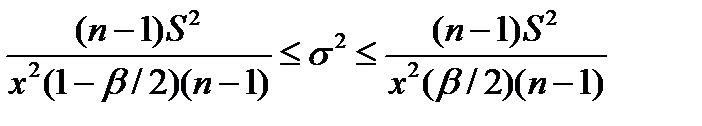
где x2(1 – β/2)(n-1) - квантиль;
x2 - квадрат распределения при вероятности P =1 – β/2 и числе степеней свободы k=n-1;
x2(β/2)(n-1) - то же для вероятности P = β/2.
Значения x2(Р)(k) находятся по таблице.
Нижняя доверительная граница для вероятности безотказной работы PH(t) может быть приближенно найдена по формуле
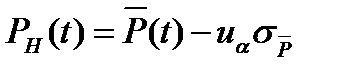
где 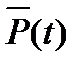 - оценка вероятности безотказной работы;
- оценка вероятности безотказной работы;
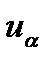 - квантиль нормального распределения;
- квантиль нормального распределения;
 - оценка стандартного отклонения оценки
- оценка стандартного отклонения оценки 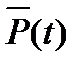 .
.
Величина 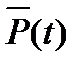 определяется по формуле
определяется по формуле
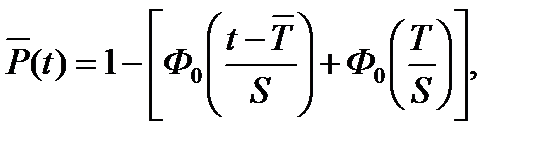
где Ф0(Z) – нормальная функция Лапласа(по таблицам).
Величина 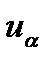 - определяется по таблицам при вероятности α.
- определяется по таблицам при вероятности α.
Величина  определяется из выражения
определяется из выражения
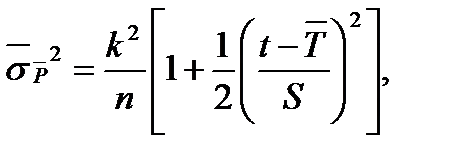
где 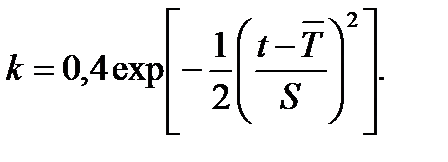
Часто при оценке надежности требуется определить границы интервала, в котором будет находится нормально распределённая случайная величина с заданной вероятностью Р.
Границы YН и YВ и интервалы часто называют толерантными (допустимыми) пределами.
Толерантные пределы запишутся следующим образом:
верхний предел [ -∞, 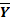 +kS ];
+kS ];
нижний предел [ 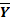 -kS,+∞ ];
-kS,+∞ ];
двусторонний интервал [ 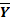 –kS,
–kS, 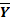 +kS ];
+kS ];
где 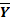 - выборочное среднее случайной величины;
- выборочное среднее случайной величины;
S – оценка стандартного отклонения.
Так как толерантные пределы определяются на основании выборочных данных 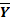 и S то они устанавливаются с вероятностью α.
и S то они устанавливаются с вероятностью α.
Константа k являющаяся функцией
a) объёма выборки n;
б) вероятности Р;
в) доверительной вероятности α
приближенно выражается функцией 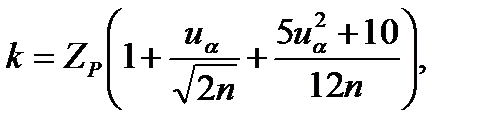
где ZP и uα – определяются по таблицам для р = Р и р = α соответственно.
Объем испытаний для определения Т с ошибкой не более ε часов с доверительной вероятностью α приближенно должен быть получен при помощи уравнения
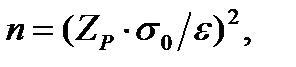
где ZP - квантиль нормального распределения, определяемый для вероятности р = α,
σ0 - ориентировочное значение σ.
Лекция 7.
Испытания ДМ для определения показателей эксплуатационных свойств





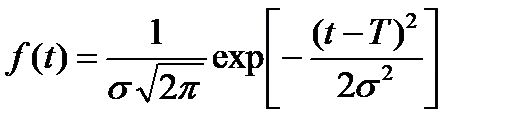

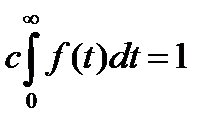
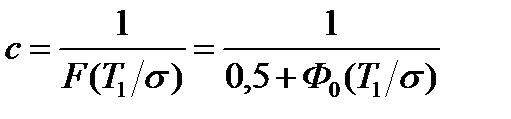
 - табулированная интегральная функция нормального распределения;
- табулированная интегральная функция нормального распределения;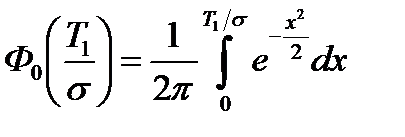 - нормированная функция Лапласа.
- нормированная функция Лапласа.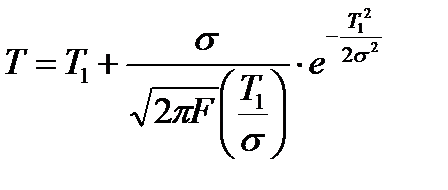
 коэффициент
коэффициент  и усеченное нормальное распределение достаточно точно аппроксимируется обычным нормальным законом.
и усеченное нормальное распределение достаточно точно аппроксимируется обычным нормальным законом.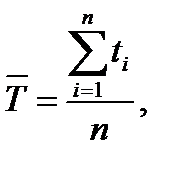


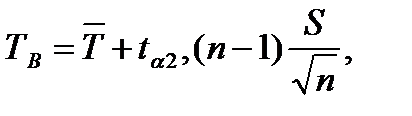
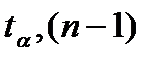 - квантиль распределения Стьюдента для вероятности α или уровня значимости β = 1 – α и числа степеней свободы f =n – 1.
- квантиль распределения Стьюдента для вероятности α или уровня значимости β = 1 – α и числа степеней свободы f =n – 1.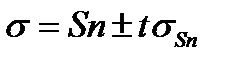

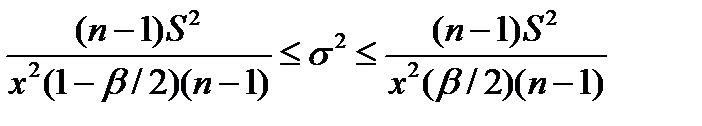
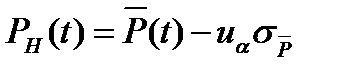
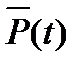 - оценка вероятности безотказной работы;
- оценка вероятности безотказной работы;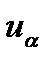 - квантиль нормального распределения;
- квантиль нормального распределения; - оценка стандартного отклонения оценки
- оценка стандартного отклонения оценки 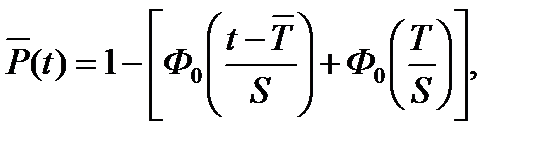
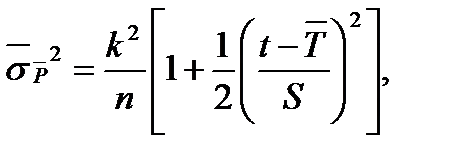
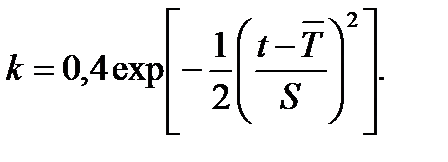
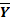 +kS ];
+kS ];