Глава 14. Модели стратегического поведения субъектов отраслевого рынка

Стратегическим называется такое поведение, когда при выборе варианта деятельности фирма принимает во внимание возможные ответные действия конкурентов. Стратегическое поведение свойственно только рынку олигополии, так как при свободной конкуренции объемы выпуска конкурентов не влияют друг на друга.

Реализация стратегического поведения фирмы происходит
в двух основных формах: в виде некооперативного и кооперативного взаимодействия.

В условиях кооперированной олигополии субъекты рынка вступают в сговор (тайный или открытый).

Рассмотрим некооперативное взаимодействие, при котором фирмы конкурируют и проводят самостоятельную политику на рынке.

В зависимости от последовательности принятия решения и от выбора фирмой стратегической переменной (цены или количества) выделяют несколько вариантов стратегического поведения фирм (табл. 14.1) [3, 5].

 

Таблица 14.1

Варианты стратегического поведения

	Стратегическая переменная
Решения принимаются фирмами по объему продаж	Решения принимаются фирмами по цене
Последовательность принятия решения фирмами	Одновременное принятие	Модель Курно	Модель Бертрана
Сначала действует фирма «лидер», а затем фирма «последователь», учитывающая ее действия	Модель Штакельберга	Модель Форхаймера

При моделировании стратегического взаимодействия фирм применяется теория игр, представляющая собой математический аппарат для принятия оптимальных решений в конфликтных ситуациях, в которых одна сторона выигрывает за счет проигрыша другой.

Если выбор решения субъекта зависит от проявления одного из возможных состояний окружающей действительности, называемой «природой», то такие игры являются «играми с природой».

Чистой стратегией в игре называется любое возможное действие какой-либо стороны или игрока.

Смешанные стратегии – это вероятности применения каждой из множества исходных стратегий. Смешанная стратегия состоит в случайном выборе одной из чистых стратегий.

Современные модели олигополии последовательно развивают идеи классической теории олигопольного ценообразования, выдвинутые А. Курно в 1838 г. и Ж. Бертраном в 1883 г. Единой модели олигополии нет. Однако существует несколько общих предпосылок для всех моделей:

– убывающая кривая спроса на продукцию олигополиста;

– взаимозависимость производителей-продавцов товаров при принятии решений относительно их поведения на рынке, то есть они могут предвидеть и учитывать поведение своих конкурентов. Однако олигополисты не знают точные кривые спроса конкурентов.

Олигополия может быть ценовой и количественной. Если олигополисты принимают решение об объеме выпуска продукции, то модель представляет количественную олигополию. Если решения принимаются по цене на продукцию, то модель рассматривает ценовую олигополию.

Модели олигополии, исходя из рационального поведения субъектов рынка, анализируют взаимодействие фирм, максимизирующих прибыль. Условия максимизации прибыли для количественной и ценовой олигополии различны.

Пусть на рынке олигополии конкурируют п фирм c объёмами производства q ₁, q ₂,..., q_n. Отраслевой спрос известен и задан функцией 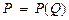,где Прибыль каждого олигополиста на рынке количественной олигополии будет зависеть от структуры предложения всех участников рынка.

.

Условие максимизации прибыли предполагает выполнение равенства [5]

.

При решении задачи на максимум прибыли каждый i -йолигополист должен учитывать значения коэффициентов вариации (при i ¹ j). Они показывают, как изменяется выпуск каждого из конкурентов при изменении выпуска i -го олигополиста на единицу [5].
В момент принятия решений олигополист должен спрогнозировать, какие решения примут другие фирмы.

Допустим, что олигополист знает предполагаемые вариации.
В этом случае он может выявить функциональную зависимость своего уровня выпуска от объемов конкурентов. Полученная зависимость определяет кривые реакции для каждого олигополиста.

Кривая реакции представляет наилучший для олигополиста ответ на действия конкурентов, то есть множество точек, соответствующих наиболее высокому уровню прибыли, которую может получить рассматриваемый олигополист при конкретной комбинации продаж конкурентов [5]. Один и тот же уровень прибыли может достигаться при различных комбинациях объемов выпуска олигополилистов. Множество таких комбинаций образуют изопрофиту. Олигополист при принятии решений рассматривает семейство изопрофит, отвечающих одному из его возможных уровней прибыли (пример семейства изопрофит для фирмы 1 на рынке с двумя продавцами представлен на рис. 14.1).

В отличие от количественной конкуренции в ценовой кривые реакции и изопрофиты рассматриваются в n -мерном пространстве цен, а не выпусков.

Коэффициенты вариации характеризуют изменения цены товара каждого из конкурентов при изменении цены i -го олигополиста на определенную величину.

 

 

а б

 

Рис. 14.1. Изопрофиты и кривые реакции фирмы 1: а – количественная конкуренция: R ₁(q ₂) – кривая реакции фирмы 1 на изменение объема продаж фирмы 2 (q ₂); б – ценовая конкуренция: R ₁(P ₂) – кривая реакции фирмы 1 на изменение цены фирмы 2 (Р ₂); П₁ ^j – прибыль фирмы 1 от различных комбинаций стратегических решений дуополистов по цене или коли­честву, которые отображаются семейством изопрофит (*); j – порядковый номер изо-

профиты

 

В данном случае изопрофиты – это множества комбинаций цен всех олигополистов, соответствующих одному и тому же уровню прибыли какого-либо олигополиста. Кривая реакции – это множество точек, соответствующих наиболее высокому уровню прибыли, которую может получить олигополист при сложившейся комбинации цен, конкурентов.

Равновесие на рынке количественной или ценовой олигополии существует, если множество точек пересечения кривых реакции всех олигополистов не является пустым.

14.1. Модель стратегического поведения
в условиях конкуренции по Штакельбергу и Курно

Исходные условия [5]:

– модель дуополии, когда на рынке взаимодействуют две фирмы;

– фирмы предлагают однородный продукт;

– фирмам известна функция рыночного спроса вида

р = а – bQ,

где a, b – положительные константы,

Q – рыночный спрос, который складывается из объёмов предложения первой и второй фирм (Q = q ₁ + q ₂) при цене Р;

– издержки производства фирм равны;

– фирмы максимизируют прибыль.

– Первой стратегический ход делает наиболее сильная фирма – «лидер», а второй – фирма-последователь.

Прибыли дуополистов определяются как разница между выручкой и издержками каждого из них

p _i = TR_i – Tc_i,

где Тс_i – издержки производства,

ТR_i – выручка фирмы;

p _i – прибыль фирмы.

Кривую рыночного спроса в линейной форме можно преобра­зовать следующим образом:

В этом случае функция прибыли каждого дуополиста будет определяться как разность между выручкой, получаемой им при сложившейся рыночной цене, и затратами на производство реализуемой на рынке продукции.

Подставив уравнение цены в уравнение прибыли, мы получим функцию прибыли для каждого дуополиста:

,

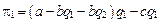Отсюда становится возможным определять изменение прибыли под влиянием его стратегических действий и при неизменном поведении конкурента.

Для того чтобы найти максимум прибыли дуополиста на рынке, необходимо полученную формулу приравнять к нулю и продифференцировать по объёму продаж:

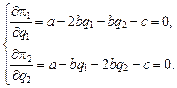
Для определения стратегического эффекта необходимо определить коэффициент вариации. При этом следует учитывать, что последователь рассматривает уровень выпуска лидера как непредсказуемый, то есть последователь принимает решение без учёта стратегического эффекта. Он максимизирует прибыль, используя кривую реакции, полученную исходя из своей функции максимума прибыли и при неизменном поведении лидера.

Для последователя кривая реакции выглядит следующим
образом:

.

Однако в отличие от последователя лидер осознаёт, что оказывает влияние на принятие его решений и поэтому учитывает реакцию последователя при решении задачи на максимум прибыли. Поскольку кривая реакции последователя известна, становится возможным определить коэффициент вариации.

При увеличении объёма продаж лидера на единицу объём продаж последователя сократится на пол-единицы. Для определения стратегического эффекта требуется умножить коэффициент вариации на производную функции прибыли фирмы лидера, взятую по объёму продаж фирмы-последователя.

.

После добавления стратегического эффекта в функцию максимума прибыли лидера она примет следующий вид (19):

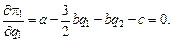
Это уравнение задаёт кривую реакции фирмы-лидера, которая
в результате преобразований примет вид

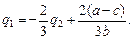
Исходя из системы полученных уравнений кривых реакций, можно определить равновесные уровни выпуска дуополистов по Штакельбергу.

.

Для подтверждения того, что фирмы получат максимум прибыли при этих объёмах продаж, необходимо дважды продифференцировать функцию прибыли по объёму производства фирмы.

, .

Поскольку частные производные функции прибыли второго порядка отрицательны, можно сделать вывод о том, что равновесные объёмы выпуска обеспечивают максимум прибыли как для дуополиста-лидера, так и для дуополиста-последователя.

При этом лидер получит прибыль в размере

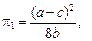
а последователь получит прибыль в два раза меньше:

Аналогичным образом моделируется стратегическое взаимодействие в условиях количественной дуополии по Курно. Однако в отличие от модели Штакельберга в модели Курно оба дуополиста рассматривают уровень выпуска конкурента как постоянный и при данной предпосылке принимают решение об уровне своего выпуска (не учитывается стратегический эффект).

Данные модели позволяют не только моделировать стратегическое поведение дуополистов, но и, например, оценивать влияние колебания валютного курса на рыночную долю фирмы при международной конкуренции [7].

Например, пусть на рынке США имеются два производителя микросхем из Японии и США. Фирмы несут одинаковые предельные издержки (с) 10$. Рынок разделен между фирмами поровну.

Пусть происходит обесценение иены на 50 %. Поскольку рынок является долларовым, изменение курса повлечет за собой изменение предельных издержек японской фирмы. Допустим, что обесценение японской валюты составляет с/ е, где е – это обменный курс иены на доллар.

50%-ное обесценение иены означает, что теперь 1 доллар равен 150 иенам. Предельные издержки японской фирмы, выраженные
в долларах США,составляют теперь 1000/150 = 6,6 доллара.

Для определения новых рыночных долей фирм воспользуемся кривой реакции Курно.

.

Пусть предельные издержки японской и американской фирмы с ₁ и с ₂ соответственно. Обе функции реакции примут вид

Подставив первое выражение в другое вместо q ₁ и применив условия равновесия 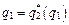, получим

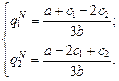
Совокупный объем производства составит

.

В итоге доля рынка японской фирмы (s ₁) определяется следующим образом:

.

Теперь, чтобы определить, как изменится рыночная доля под влиянием обесценения иены, подставим в формулу е.

.

Параметр а берется из функции спроса: р = а – bQ.

 

14.2. Ценовая конкуренция по Бертрану
и «дилемма заключенного»

Исходные условия для формирования модели [5]:

– дуополия;

– средние издержки двух фирм равны и постоянны;

– цены фирмы устанавливают одновременно;

– функция рыночного спроса При этом функция спроса одного из дуополистов имеет вид

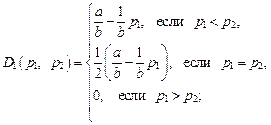
– имеется рынок однородной продукции.

Каждый дуополист в целях увеличения объёма продаж будет снижать цену своей продукции на малую величину. В конечном счёте равновесие в модели дуополии Бертрана установится в точке пересечения кривых реакции конкурентов, в которой они могут получить нулевую прибыль. В этом случае будет иметь место парадокс Бертрана.

Его суть в том, что при появлении всего одной конкурирующей фирмы рыночное равновесие может стать нестабильным и привести к «ценовой войне», а следовательно, и к конкурентному результату, то есть к нулевой прибыли в долгосрочном периоде, что нейтрализует стимулы крупных фирм к производству и сбыту данного товара.

В рамках теории игр парадокс Бертрана известен как «дилемма заключенного». Виновные в совершении преступления стоят перед выбором стратегии «сознаваться» или «не сознаваться» и делают выбор одновременно, изолированно друг от друга. При этом они не доверяют друг другу. Результаты их возможного выбора представлены в табл. 14.2 [3, 5].

 

Таблица 14.2

Матрица выигрышей «заключенных»

	Заключенный 2
Сознаться	Не сознаться
Заключенный 1	Сознаться	Срок: (5 лет; 5 лет)	Срок: (1 год; 10 лет)
Не сознаться	Срок: (10 лет; 1 год)	Срок: (2 года; 2 года)

 

Для каждого из них доминирующей стратегией или стратегией, приносящей наибольший выигрыш при любой стратегии другого игрока, является стратегия «сознаваться». Каждый заключенный думает, что другой признается первым и обречет его на более суровое наказание. Рациональный выбор обоих будет состоять в том, чтобы сознаться, несмотря на возможность улучшить положение обоих при выборе ими стратегии «не сознаваться».

Подобным образом не доверяют друг другу и фирмы. Они так же, как и заключенные, не могут принудить друг друга к выполнению достигнутых договоренностей. Рассмотрим пример стратегического взаимодействия фирм по цене. Возможные комбинации их стратегий и получаемых ими выигрышей представлены в виде матрицы выигрышей в табл. 14.3.

Таблица 14.3

Матрица выигрышей «игрока»

	Стратегии фирмы 2
Низкая цена: 5	Высокая цена: 10
Стратегии фирмы 1	Низкая цена: 5	(2; 2)	(4; 1)
Высокая цена: 10	(1; 4)	(3; 3)

 

В однопериодной игре доминирующей стратегией для каждой фирмы будет стратегия «назначать низкую цену». Равновесие рынка с низкими ценами будет служить равновесием по Нэшу (американский математик Джон Нэш) в неповторяющейся игре.

Равновесие по Нэшу – это такое состояние рынка, при котором каждое предприятие придерживается стратегии, являющейся наилучшим ответом на стратегии других конкурентов. То есть ни одно предприятие не хочет изменить своего поведения в одностороннем порядке.

Если игра или стратегическое взаимодействие фирм продолжается бесконечно долго, то доминирующими будут по крайней мере две стратегии.

1. Стратегия «руки, дрожащей на курке» – назначить высокую цену в момент t, если другая фирма назначила высокую цену в момент (t – 1), и наоборот.

2. Стратегия «хищничества» – назначать низкую цену в любой момент времени.

Максимальный выигрыш каждой фирмы в результате применения первой стратегии определяется с учетом ценности прибыли, получаемой в бесконечном периоде и приведенной к текущему моменту времени.

где 3–прибыль, полученная фирмой, назначающей цену 10 руб./ед. прод., при условии, что другая фирма назначает эту же цену;

d – дисконтирующий множитель, связанный со ставкой дисконтирования: d = l/(l + i), i – процентная ставка; r – вероятность взаимодействия фирм в следующем периоде (t + 1).

Поскольку после установления фирмой 2 низкой цены в первом периоде цена фирмы 1 во втором периоде тоже будет низкой, мак­симальный выигрыш фирмы от применения стратегии низкой цены

где 4 – прибыль, полученная фирмой 2, назначающей низкую цену, при условии, что фирма 1 назначает высокую цену;

2 – прибыль, полученная фирмой 2, назначающей низкую цену, при условии, что фирма 1 назначит низкую цену со второго периода.

Следовательно, выбор оптимальной стратегии фирмы, зависит от наибольшей величины выигрыша

14.3. Модель Бертрана
для дифференцированного продукта

Модель показывает, что дифференциация продукта смягчает ценовую конкуренцию. При этом соперничество фирм не ведет
к полному исчезновению их прибылей. Пусть функция спроса первого дуополиста имеет вид [5]

где a ₁, b ₁, z ₁ – положительные константы.

При этом0 < z ₁ < b ₁ и a ₁ > с (b ₁– z ₁).

Условие z ₁< b ₁ означает, что если цены товаров обеих фирм вырастут на бесконечно малую величину e, объем спроса на оба товара сократится. Условие a ₁ > AC (b ₁ – z ₁)означает, что если обе фирмы назначат цены на уровне предельных издержек, объемы спроса на их товары будут положительными.

Естественно, что при понижении цены р ₁ первый дуополист увеличит выпуск, а понижение цены конкурента наоборот вызывает снижение выпуска первого дуополиста. Функция прибыли дуополиста имеет вид

где с – затраты предприятия на единицу продукции.

Следует заметить, что при принятии дуополистами решений
о ценообразовании ими будет учитываться уровень цены, установленный на предыдущем шаге. При этом в силу предпосылок модели Бертрана дуополисты принимают решения при нулевых коэффициентах вариации.

Таким образом, необходимое условие максимизации прибыли примет вид

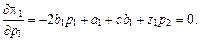
Оно задаёт кривую реакции первого дуополиста

По аналогии можно представить функцию спроса и кривую реакции для второго дуополиста.