Исследование олигопольного рынка

На олигопольном рынке только несколько фирм производят всю или почти всю продукцию. Фирмы зарабатывают значительную прибыль на долговременном этапе, потому что ограничение доступа на олигопольный рынок делает сложным или невозможным выход на рынок новых фирм. Олигополия является преобладающей формой современной рыночной структуры. Олигопольными отраслями являются автомобильная промышленность, производство стали, нефтехимикатов, электрооборудования и др.

Рассмотрим модель О. Курно для олигопольного рынка. Предположим, фирмы производят однородный товар и знают кривую рыночного спроса. Каждая фирма должна решить, сколько продукции выпускать. Причем все фирмы принимают свои решения в одно и то же время, т.е. изменение объема в одной фирме не влияет на решение производственных вопросов других фирм. Но конечная цена на рынке будет зависеть от совокупного объеме производства всех фирм.

Для олигопольного рынка исследуем, от чего зависит объем производства, максимизирующий прибыль каждой фирмы, и как складывается цена рынке.

Пусть на рынке n фирм.

Обозначим х ₁, х ₂, …, х_n – издержки производства каждой фирмы, у ₁, у ₂, …, у_n – объем производства каждой фирмы.

Тогда у = у ₁ + у ₂ + … + у_n – совокупность объема производства всех фирм (объем продаж).

Известная кривая рыночного спроса

Р = a – ву, а > 0, в > 0, (1.18)

где Р – цена ед. продукции;

у – совокупный объем производства;

а, в – параметры (известные величины).

Кривая спроса (1.18) показывает, что с увеличением объема продаж цена ед. продукции снижается. Зависимость линейная.

Допустим, издержки производства каждой фирмы также линейно зависят от объема выпускаемой продукции. Эта зависимость (для простоты) имеет одинаковый вид для всех фирм.

Пусть издержки производства i -й фирмы представлены следующим образом:

х_i = су_i + d, i = 1, 2, …, n, (1.19)

где у_i – объем производства i -й фирмы,

c, d > 0 – параметры функции (известные величины).

Рассмотрим действия каждой фирмы.

Фирма 1. Прибыль фирмы (p₁) представляет собой разницу между доходом R ₁ и издержками производства х ₁:

p₁ = R ₁ – x ₁ = Py ₁ – x ₁.

Подставим в это выражение кривую спроса (1.18) и функции издержек (1.19).

p₁= (а – ву) · у ₁ – (су ₁ + d).

Учитывая, что у = у ₁ + у ₂ + … + у_n, имеем

p₁= [ а – в (у ₁ + у ₂ + … + у_n)] · у ₁ – су ₁ – d.

Получили, что прибыль фирмы 1 зависит от своего объема выпуска продукции у ₁, а также от объемов производства других фирм.

Будем искать максимум прибыли фирмы 1 при условии, что остальные фирмы не реагируют на её действия, на изменение её объема, т.е.

, i = 2, 3, …, n.

Функция прибыли p₁ принимает максимальное значение в критической точке, которую можно найти, если производную от функции p₁ по у ₁ приравнять нулю, т.е.

p' _{у 1}= 0.

Получим

– ву ₁ + а – в (у ₁ + у ₂ +…+ у_n) – c = 0. (1.20)

Это условие максимума прибыли фирмы 1.

Фирма 2. Аналогично прибыль

p₂ = R ₂ – x ₂ = [ a – в · (у ₁ + у ₂ + … + у_n)] · у ₂ – су ₂ – d.

Производную от p₂ по у ₂ приравниваем к нулю,

p' _{у 2}= 0.

Получим

– ву ₂ + а – в · (у ₁ + у ₂ + … + у_n) – c = 0. (1.21)

Это условие максимума прибыли фирмы 2 и т.д.

– ву_i + а – в (у ₁ + у ₂ + … + у_n) – c = 0. (1.22)

Условие максимума прибыли любой i -й фирмы.

Из (1.20) вычтем (1.21.), получим у ₁ = у ₂.

Из (1.21) вычтем (1.22), получим у ₂ = у ₁.

Таким образом, каждая фирма достигает максимальной прибыли на олигопольном рынке, если объемы производства всех фирм одинаковы. Это понятно, так как издержки производства одинаково зависят от объема производства (1.19).

Следовательно, у = n · у_i.

Найдем объем производства хотя бы одной фирмы, например фирмы 1. Тогда, подставив (1.23) в (1.19), получим

– ву ₁ + а – впу ₁ – с = 0.

Отсюда

y ₁ = 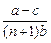. (1.24)

Совокупный объем производства всех фирм в n раз больше:

y = 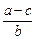· . (1.25)

Зная кривую спроса (1.18) и объем продаж на рынке (1.25), определим цену, по которой будет реализована продукция.

Р = а – by = a – b · 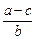· . (1.26)

Получили, что цена на рынке не зависит от условно-постоянных расходов d.

Определим прибыль фирмы 1 следующим образом:

p₁ = Ру ₁ – х ₁ = Ру ₁ – су ₁ – d.

Подставив в это выражение оптимальный объем производства фирмы 1 (1.24) рыночную цену (2.26), получим

p₁ =

Таким образом, получили выражение максимальной прибыли фирмы 1

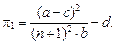(1.27)

Точно такую же прибыль получат все фирмы, так как объемы продаж одинаковы.

Вывод для олигопольного рынка. Если рыночная цена линейно зависит от совокупного объема продаж (1.18) и производственные издержки каждой фирмы линейно зависят от её объема производства (1.19.), то оптимальный объем производства, рыночная цена, максимальная прибыль находятся по формулам (1.25)–(1.27).

Монопольный рынок можно рассматривать как частный случай олигополии при n = 1. Если цена описывается уравнением

Р = а – ву, а > 0, в > 0,

где Р – цена ед. продукции; у – объем выпускаемой продукции
и производственные издержки фирмы линейно зависят от её объема производства

х = су = d,

то оптимальные показатели деятельности фирмы-монополиста можно вычислить по следующим формулам.

Объем выпускаемой продукции

(1.28)

Цена единицы продукции

. (1.29)

Максимальная прибыль

(1.30)

Формулы получены из (1.25.)–(1.27) путем подстановки n = 1.

Исследуем, как изменяются показатели оптимальный объем продаж, цена, прибыль с увеличением числа фирм на рынке.

При n ®  ¥ имеем идеально конкурентный рынок.

Цена

P = ,

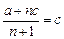а при монополии Р = (а + с)/2, причем а > с, т.е. цена уменьшается.

Таким образом, с увеличением числа фирм на рынке цена падает и стремится к предельным издержкам.

Объем продаж

y = a > c,

а при монополии

.

Причем > .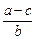

Таким образом, совокупный объем продаж с увеличением числа фирм на рынке возрастает и стремится к величине (а – с)/ b.

Прибыль любой фирмы

уменьшается с увеличением числа фирм и может принять отрицательное значение. При сильно раздробленном рынке фирмы могут оказаться нерентабельными. Можно определить максимальное число фирм (n) на рынке, при котором прибыль каждой фирмы будет
не отрицательной. Для этого надо решить уравнение (1.31) относительно n.

(1.31)

Числовой пример по определению максимального числа фирм:

Пусть кривая спроса имеет вид

Р = 100 – 0,01 у.

Функция издержек производства

х = 50 у + 10 000.

Определить максимальное число фирм, при котором прибыль
не отрицательна.

Итак, а = 100; b = 0,01; d = 10 000.

Подставив эти значения в уравнение (1.31), получим

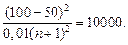
Отсюда n + 1 = 5 или n = 4.

Максимальное число фирм равно четырем.

С увеличением числа фирм на рынке и общая масса прибыли уменьшается. Таким образом, раздробление рынка на большое число мелких фирм не эффективно.

Если число фирм растет, то неустойчиво общее состояние на рынке, появляется угроза банкротства, что подталкивает фирмы либо к объединению, либо к устранению конкурента «Стремление к максимуму прибыли есть стремление избавиться от конкурента, т.е.
к монополии» (Адам Смит). Поэтому в рыночной системе хозяйствования для противовеса необходимы государственные антимонопольные меры.

 

 

 

 

II. Практические ситуации