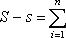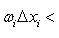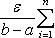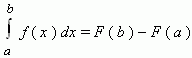Интегрируемость непрерывных функций

Докажем следующую основную теорему.

Теорема. Непрерывная на сегменте [ a, b ] функция f (x) интегрируема на этом сегменте.

Доказательство. Пусть дано любое ε > 0. В силу равномерной непрерывности функции f (x) на сегменте [ a, b ] для положительного числа ε /(b - a) можно указать такое δ > 0, что при разбиении T сегмента [ a, b ] на частичные сегменты [ x_{i -1}, x_i ], длины Δ x_i которых меньше δ, колебание ω_i функции f (x) на каждом таком частичном сегменте будут меньше ε /(b - a). Поэтому для таких разбиений T

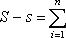
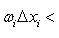
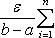
Следовательно, для непрерывной на сегменте [ a, b ] функции f (x) выполнены достаточные условия интегрируемости.

Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.

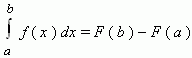
Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x), вычислить ее значения в точках a и b и найти разность F(b) – F(a).

Методические особенности введения определения интеграла.

Тема изучается в 11 классе и главное её назначение – обучить учащихся вычислению площади криволинейной трапеции и других более сложных фигур и вычислять объемы геометрического тела с помощью интеграла. Значимость этой темы в том, что интегрирование или отыскание первообразной – это обратная задача отыскания производной. До изучения этой темы учащиеся могли выполнять над функциями следующие действия: сложение, вычитание, умножение и деление. После изучения этой темы учащиеся должны будут уметь выполнять новые действия: дифференцирование.

Изучение этой темы завершает школьный курс математического анализа

Данная тема включает в себя следующие вопросы: первообразная, основное свойство первообразной, три правила нахождения первообразных, площадь криволинейной трапеции, интеграл, формула Ньютона – Лейбница, применение интеграла.

Существует два способа введения понятия интеграла: 1 способ-рассмотрение интеграла как приращения первообразной; Например в учебнике А.Н. Колмогорова., и 2 способ-рассмотрение интеграла как предела интегральных сумм. Например, учебник Алимов Ш.А.

Наиболее трудный, недоступный для школьников – второй подход, так как теория пределов в школе не изучается. В школе используются первый подход. S_кр.тр.=F(b)-F(a) – такой подход реализован в современных учебниках.

Сравнительный анализ содержания темы в школьных учебниках

В учебнике А. Н. Колмогорова «Алгебра и начала анализа» при введении интеграла рассматривается задача о вычислении площади криволинейной трапеции. Автор приводит в учебнике два способа вычисления площади криволинейной трапеции: с помощью теоремы о площади криволинейной трапеции и с помощью интегральных сумм. Второй способ сводится к определению интеграла. С помощью интегральных сумм выводятся также формулы для вычисления объемов тел, работы переменной силы, а также нахождения массы стержня и центра масс.

В учебнике Мордковича А. Г. «Алгебра и начала анализа» при введении понятия «Определенный интеграл» рассматриваются задачи, приводящие к данному понятию, а именно задача о вычислении площади криволинейной трапеции, задача о вычислении массы стержня и задача о перемещении точки. Все три задачи при их решении приводятся к одной и той же математической модели.

В учебнике Никольского С. М. «Алгебра и начала анализа» рассмотрение задачи о вычислении площади криволинейной трапеции приводит к понятию интегральных сумм и пределу от них, после чего вводится определение определенного интеграла. Теоретическое обоснование применения определенного интеграла рассматривается в таких физических задачах, как задачи на работу силы, работу электрического заряда, на вычисление массы стержня переменной плотности, давления жидкости на стенку и центра тяжести.

В учебнике Ш. А. Алимова «Алгебра и начала анализа» перед введением понятия интеграла рассматривается задача о нахождении площади криволинейной трапеции, где вычисление площади сводится к отысканию первообразной F(х) функции f(x). Разность F(b)- F(a) называют интегралом от функции f(x) на отрезке [a; b]. Далее автор рассматривает вычисление площади криволинейной трапеции с помощью интегральных сумм, говорит о том, что такой способ приближенного вычисления интеграла требует громоздких вычислений и им пользуются в тех случаях, когда не удается найти первообразную функции. В качестве примеров применения интеграла приведены задачи о вытекании воды из бака и нахождении работы силы. Задачи для самостоятельного решения однотипны и их очень мало.