Плоскость, на которой выполняется абсолютная геометрия и постулат Лобачевского, принято называть плоскостью Лобачевского.
Простейшие факты геометрии Лобачевского в схеме Гильберта: При доказательстве теорем будем использовать аксиомы I-IV групп Гильберта, т.е. аксиомы абсолютной геометрии и аксиому Лобачевского.
Т-ма1: Во всяком треугольнике АВС сумма внутренних углов меньше 180° (sАВС<2d).
Следствие: Во всяком простом четырехугольнике сумма внутренних углов меньше 4d.
Т-ма2: Сумма внутренних углов треугольника непостоянна, т.е. не одна и та же для всех треугольников.
Док-во: 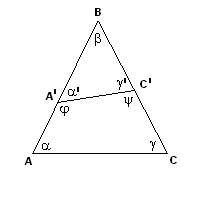 Предположим противное: s - постоянная. Пусть А¢ и С¢ внутренние точки отрезка АВ и ВС, получим треуго-ик А¢ВС¢. Делаем предположение, что sАВС=sА¢ВС¢Þa¢+β+g¢ =a+β+gÞa¢+g¢ =a+g (1). С другой стороны a¢+j=2d; g¢+y=2dÞ (a¢+g¢)+j+y=4d (1)Þa+g+j+y=4d – противоречие со следствием Þ предположение не верно. Теорема доказана.
Предположим противное: s - постоянная. Пусть А¢ и С¢ внутренние точки отрезка АВ и ВС, получим треуго-ик А¢ВС¢. Делаем предположение, что sАВС=sА¢ВС¢Þa¢+β+g¢ =a+β+gÞa¢+g¢ =a+g (1). С другой стороны a¢+j=2d; g¢+y=2dÞ (a¢+g¢)+j+y=4d (1)Þa+g+j+y=4d – противоречие со следствием Þ предположение не верно. Теорема доказана.
В абсолютной геометрии можно доказать 3 признака равенства треугольников. В геометрии Лобачевского справедлив и 4й признак.
Т-ма3: (4й признак равенства треугольников): Если 3 угла одного треугольника соответственно равны 3м углам другого треугольника, то эти треуг-ки равны.
Т-ма4: Пусть прямые а и а ¢ лежат в одной плоскости и не пересекаются, т-ки А, В, С Î а, причем m(АВС), А¢, В¢ - ортогональные проекции точек А и В на прямую а ¢, тогда ÐА¢АС<ÐВ¢ВС.
Т-ма 5: Пусть на плоскости даны прямая а и не лежащая не ней (.)А. Существует бесконечное множество прямых этой плоскости, проходящих через т-ку А и не пересекающих прямую а.
Взаимное расположение прямых на плоскости Лобачевского. Выберем прямую а и не лежащую на ней (.)А. Проведем перпендикуляр АВ к а. Проведем перпенд. АС к прямой АВ. Согласно Т-ме5 через А проходит бесконечное множ-во прямых не пересекающих прямую а. Прямая АС одна из этих прямых. Разобьем мн-во всех точек отрезка ВС на 2 класса: К1={МÎВС½АМÇ а ¹Æ}, К2={МÎВС½АМÇ а =Æ}. Указанное разбиение удовлетворяет условиям аксиомы Дедекинда. Тогда существует (.)L, которая производит Дедекиндово сечение, т.е. для любых точек ХÎВС: если m(ВХL), то ХÎК1, а если m(LХC), то ХÎК2.
 Опр: Прямые AL и AL¢ называются параллельными прямой а, если выполняются 2 условия: 1)они не пересекают прямую а 2)все прямые пучка p(А) (p с центром А) лежащие внутри 1ой пары вертикальных углов, образованных прямыми AL и AL¢ пересекают а, а все прямые лежащие внутри другой пары не пересекают а.
Опр: Прямые AL и AL¢ называются параллельными прямой а, если выполняются 2 условия: 1)они не пересекают прямую а 2)все прямые пучка p(А) (p с центром А) лежащие внутри 1ой пары вертикальных углов, образованных прямыми AL и AL¢ пересекают а, а все прямые лежащие внутри другой пары не пересекают а.
Опр: ÐBAL=a называется углом параллельности на плоскости Лобачевского в (.)А относительно прямой а.
Опр: прямые b и а называются расходящимися (сверхпараллельными) если они не параллельны и не пересекаются.
Модель Кэли-Клейна - первая модель геометрии Лобачевского; с её помощью удалось доказать непротиворечивость геометрии Лобачевского в предположении непротиворечивости Евклидовой геометрии.
Плоскость Лобачевского представляется внутренностью круга (черт.34), прямые – хордами (с исключенными концами, поскольку рассматривается только внутренность круга).

Пусть на проективной плоскости введены проективные координаты  и задана некоторая овальная линия второго порядка, обозначаемая дальше буквой k, например
и задана некоторая овальная линия второго порядка, обозначаемая дальше буквой k, например 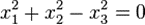 .
.
Каждое проективное отображение проективной плоскости на себя, которое оставляет на месте линию k, называется автоморфизмом относительно k. Каждый автоморфизм отображает внутренние точки линии k также во внутренние её точки. Множество всех автоморфизмов относительно линии k составляет группу. Пусть рассматриваются только точки проективной плоскости, лежащие внутри k; хорды линии k называются «прямыми». Две фигуры пусть считаются равными, если одна из них переводится в другую некоторым автоморфизмом. Так как автоморфизмы составляют группу, то имеют место основные свойства равенства фигур: если фигура А равна фигуре В, то В равна А; если фигура А равна фигуре В, а В равна фигуре С, то А. равна С.В получаемой т. о. геометрические теории будут соблюдены требования всех аксиом евклидовой геометрии, кроме аксиомы о параллельных: вместо этой последней аксиомы соблюдается аксиома о параллельных Лобачевского (см. рисунок). Тем самым получается истолкование (двумерной) геометрии Лобачевского при помощи объектов проективной плоскости или, как говорят, проективная модель геометрии Лобачевского; линию k называют абсолютом этой модели. Автоморфизмы относительно k играют роль движений.






 Предположим противное: s - постоянная. Пусть А¢ и С¢ внутренние точки отрезка АВ и ВС, получим треуго-ик А¢ВС¢. Делаем предположение, что sАВС=sА¢ВС¢Þa¢+β+g¢ =a+β+gÞa¢+g¢ =a+g (1). С другой стороны a¢+j=2d; g¢+y=2dÞ (a¢+g¢)+j+y=4d (1)Þa+g+j+y=4d – противоречие со следствием Þ предположение не верно. Теорема доказана.
Предположим противное: s - постоянная. Пусть А¢ и С¢ внутренние точки отрезка АВ и ВС, получим треуго-ик А¢ВС¢. Делаем предположение, что sАВС=sА¢ВС¢Þa¢+β+g¢ =a+β+gÞa¢+g¢ =a+g (1). С другой стороны a¢+j=2d; g¢+y=2dÞ (a¢+g¢)+j+y=4d (1)Þa+g+j+y=4d – противоречие со следствием Þ предположение не верно. Теорема доказана. Опр: Прямые AL и AL¢ называются параллельными прямой а, если выполняются 2 условия: 1)они не пересекают прямую а 2)все прямые пучка p(А) (p с центром А) лежащие внутри 1ой пары вертикальных углов, образованных прямыми AL и AL¢ пересекают а, а все прямые лежащие внутри другой пары не пересекают а.
Опр: Прямые AL и AL¢ называются параллельными прямой а, если выполняются 2 условия: 1)они не пересекают прямую а 2)все прямые пучка p(А) (p с центром А) лежащие внутри 1ой пары вертикальных углов, образованных прямыми AL и AL¢ пересекают а, а все прямые лежащие внутри другой пары не пересекают а.
 и задана некоторая овальная линия второго порядка, обозначаемая дальше буквой k, например
и задана некоторая овальная линия второго порядка, обозначаемая дальше буквой k, например 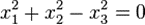 .
.



