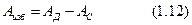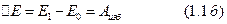Кинетическая энергия механизма складывается из суммы кинетических энергий его звеньев. Кинетическая энергия каждого звена в общем случае движения состоит из двух частей: кинетической энергии в поступательном движении звена и кинетической энергии во вращательном движении:
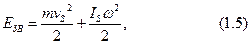
где
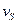 — скорость центра тяжести звена;
— скорость центра тяжести звена;
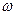 — угловая скорость звена;
— угловая скорость звена;
m — масса звена;
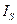 — момент инерции звена относительно оси, проходящей через его центр тяжести.
— момент инерции звена относительно оси, проходящей через его центр тяжести.
Кинетическая энергия всех звеньев механизма равна
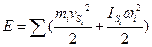
Разделим и умножим правую часть равенства на квадрат скорости точки приведения А:
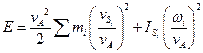
Выражение, стоящее в квадратных скобках, как легко видеть, имеет размерность массы. Обозначим
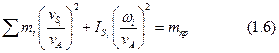
Тогда
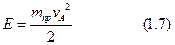
т. е. кинетическая энергия механизма может быть выражена через кинетическую энергию некоторой условной приведенной массы mпр, которая как бы сосредоточена в точке приведения А звена приведения (см. рис. 1.2).
Таким образом, приведенной массой механизма называется такая условная масса, которая как бы сосредоточена в точке приведения механизма, кинетическая энергия которой равна сумме кинетических энергий всех звеньев механизма.
Формулу (1.7) можно написать иначе:
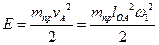
Но 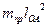 есть момент инерции приведенной массы относительно оси вращения звена приведения. Обозначим
есть момент инерции приведенной массы относительно оси вращения звена приведения. Обозначим
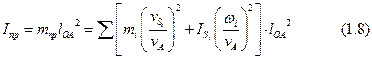
тогда
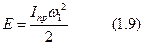
т. е. кинетическая энергия механизма может быть также выражена через кинетическую энергию некоторого условного приведенного момента инерции Iпр, которым как бы обладает звено приведения (см. Рис. 1.3).
Таким образом, приведенным моментом инерции механизма называется такой условный момент инерции, которым как бы обладает звено приведения относительно оси вращения, кинетическая энергия которого (при таком моменте инерции) равна сумме кинетических энергий всех звеньев механизма.
Из формул (1.6) и (1.8) видно, что приведенная масса 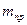 и приведенный момент инерции Iпр механизма есть величины переменные и зависят (кроме постоянных масс и моментов инерции отдельных звеньев) от положения механизма (так как отношения скоростей зависят только от положения механизма).
и приведенный момент инерции Iпр механизма есть величины переменные и зависят (кроме постоянных масс и моментов инерции отдельных звеньев) от положения механизма (так как отношения скоростей зависят только от положения механизма).
Следует отметить, что если звено приведения совершает поступательное движение, то для исследования его движения нужно определять приведенную к нему массу mпр, а если оно совершает вращательное движение (таких ведущих звеньев большинство), то для исследования его движения удобнее определять приведенный момент инерции Iпр.
Таким образом, после приведения к ведущему звену всех сил (и моментов сил) и всех масс (и моментов инерции) звеньев, исследование движения сложного механизма сводится к рассмотрению движения одного лишь ведущего звена по схеме, изображенной на рис. 1.2, или по схеме, изображенной на рис. 1.3, где приведенная сила (или момент силы) и масса (или момент инерции) в общем случае есть величины переменные.
Уравнение движения машины
После приведения всех масс и моментов инерции, а также всех сил и моментов сил к ведущему звену кинетическую энергию механизма можно выразить через кинетическую энергию приведенной массы (или приведенного момента инерции), а работу всех сил — через работу приведенной силы (или приведенного момента силы). Тогда уравнение (1.1а) примет вид:
для схемы по рис. 1.2
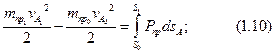
для схемы по рис. 1.3
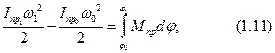
где 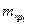 — приведенная к точке А ведущего звена масса механизма, соответствующая его положению в конце рассматриваемого периода;
— приведенная к точке А ведущего звена масса механизма, соответствующая его положению в конце рассматриваемого периода;
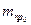 — приведенная к точке А ведущего звена масса механизма, соответствующая его положению в начале рассматриваемого периода;
— приведенная к точке А ведущего звена масса механизма, соответствующая его положению в начале рассматриваемого периода;
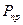 — приведенная к ведущему звену сила;
— приведенная к ведущему звену сила;
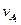 — скорость точки А ведущего звена в конце периода;
— скорость точки А ведущего звена в конце периода;
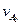 — скорость точки А ведущего звена в начале периода;
— скорость точки А ведущего звена в начале периода;
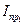 — приведенный к ведущему звену момент инерции механизма в конце рассматриваемого периода;
— приведенный к ведущему звену момент инерции механизма в конце рассматриваемого периода;
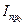 — приведенный к ведущему звену момент инерции механизма в начале рассматриваемого периода;
— приведенный к ведущему звену момент инерции механизма в начале рассматриваемого периода;
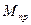 — приведенный к ведущему звену момент силы;
— приведенный к ведущему звену момент силы;
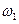 — угловая скорость ведущего звена в конце периода;
— угловая скорость ведущего звена в конце периода;
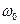 — угловая скорость ведущего звена в начале периода.
— угловая скорость ведущего звена в начале периода.
Мы в дальнейшем будем пользоваться в основном уравнением (1.11) и схемой, изображенной на рис. 1.3, так как большинство ведущих звеньев совершает вращательное движение, для которого этими уравнением и схемой пользоваться удобнее.
Перепишем правые части уравнений (1.10) и (1.11) несколько иначе. В теории механизмов и машин будем различать движущие силы и силы сопротивления. Напомним, что движущие силы направлены в сторону движения и их работы считаются положительными, а силы сопротивления направлены противоположно движению и их работы считаются отрицательными. Произведя приведение этих сил к ведущему звену в отдельности, уравнения (1.10) и (1.11) будут иметь вид:
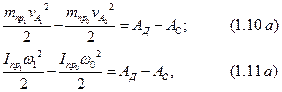
где 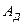 — работа движущих сил;
— работа движущих сил;
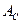 — работа сил сопротивления.
— работа сил сопротивления.
Но 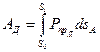 или
или 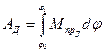
И
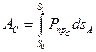 или
или 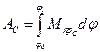
Тогда уравнения движения примут вид:
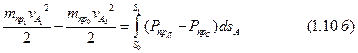
И
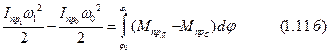
Для удобства дальнейшего изложения разность между работами движущих сил 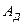 и сил сопротивления
и сил сопротивления 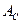 назовем избыточной работой и обозначим
назовем избыточной работой и обозначим 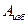 :
:
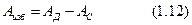
Тогда уравнение движения в общем виде будет иметь вид
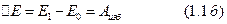





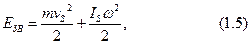
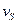 — скорость центра тяжести звена;
— скорость центра тяжести звена;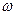 — угловая скорость звена;
— угловая скорость звена;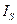 — момент инерции звена относительно оси, проходящей через его центр тяжести.
— момент инерции звена относительно оси, проходящей через его центр тяжести.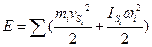
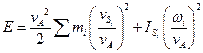
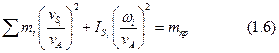
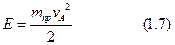
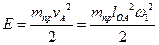
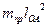 есть момент инерции приведенной массы относительно оси вращения звена приведения. Обозначим
есть момент инерции приведенной массы относительно оси вращения звена приведения. Обозначим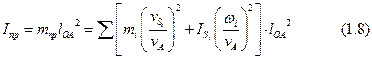
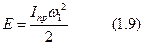
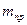 и приведенный момент инерции Iпр механизма есть величины переменные и зависят (кроме постоянных масс и моментов инерции отдельных звеньев) от положения механизма (так как отношения скоростей зависят только от положения механизма).
и приведенный момент инерции Iпр механизма есть величины переменные и зависят (кроме постоянных масс и моментов инерции отдельных звеньев) от положения механизма (так как отношения скоростей зависят только от положения механизма).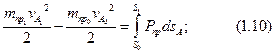
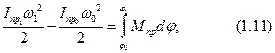
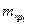 — приведенная к точке А ведущего звена масса механизма, соответствующая его положению в конце рассматриваемого периода;
— приведенная к точке А ведущего звена масса механизма, соответствующая его положению в конце рассматриваемого периода;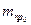 — приведенная к точке А ведущего звена масса механизма, соответствующая его положению в начале рассматриваемого периода;
— приведенная к точке А ведущего звена масса механизма, соответствующая его положению в начале рассматриваемого периода;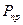 — приведенная к ведущему звену сила;
— приведенная к ведущему звену сила;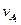 — скорость точки А ведущего звена в конце периода;
— скорость точки А ведущего звена в конце периода;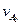 — скорость точки А ведущего звена в начале периода;
— скорость точки А ведущего звена в начале периода;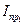 — приведенный к ведущему звену момент инерции механизма в конце рассматриваемого периода;
— приведенный к ведущему звену момент инерции механизма в конце рассматриваемого периода;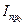 — приведенный к ведущему звену момент инерции механизма в начале рассматриваемого периода;
— приведенный к ведущему звену момент инерции механизма в начале рассматриваемого периода;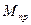 — приведенный к ведущему звену момент силы;
— приведенный к ведущему звену момент силы;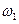 — угловая скорость ведущего звена в конце периода;
— угловая скорость ведущего звена в конце периода;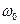 — угловая скорость ведущего звена в начале периода.
— угловая скорость ведущего звена в начале периода.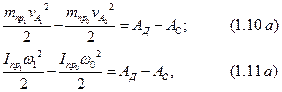
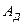 — работа движущих сил;
— работа движущих сил;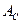 — работа сил сопротивления.
— работа сил сопротивления.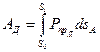 или
или 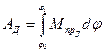
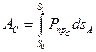 или
или 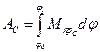
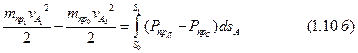
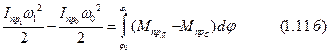
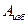 :
: