При решении задач силового расчета механизмов предполагаются известными закон движения ведущего звена, массы и моменты инерции звеньев механизма. Таким образом, всегда могут быть определены те силы инерции, которые необходимы для решения задач силового расчета с помощью уравнений равновесия.
Кинетостатика механизмов занимается решением двух задач: определением усилий (реакций) в кинематических парах; определением так называемых уравновешивающих сил.
Без знания сил, найденных путем кинетостатического расчета, нельзя рассчитывать детали машин на прочность и износ, подбирать подшипники, определять необходимую мощность и коэффициент полезного действия. В качестве примера приведем силовой расчет шестизвенного механизма с ведущим звеном l, с известными массами звеньев т и силой полезного сопротивления 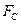 .
.
Кинетостатический расчет механизма начинают с группы Ассура, наиболее удаленной от ведущего звена, и проводят его последовательно согласно формуле строения 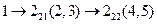 .
.
Рассмотрим расчет группы 222 (звенья 4, 5). Силы тяжести 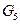 и
и 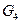 звеньев 5 и 4 приложены в центрах тяжести в точках
звеньев 5 и 4 приложены в центрах тяжести в точках 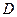 и
и 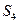 и направлены вертикально вниз. Так как группы Ассура являются статически определимыми кинематическими цепями, то, применяя принцип Даламбера, сводим задачу динамики к задаче статики. Рассматриваемая группа освобождена от связей. Вместо них надо приложить соответствующие реакции:
и направлены вертикально вниз. Так как группы Ассура являются статически определимыми кинематическими цепями, то, применяя принцип Даламбера, сводим задачу динамики к задаче статики. Рассматриваемая группа освобождена от связей. Вместо них надо приложить соответствующие реакции: 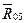 — реакцию, действующую в поступательной паре со стороны стойки на звено 5 и
— реакцию, действующую в поступательной паре со стороны стойки на звено 5 и 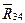 — реакцию, действующую в шарнире С со стороны звена 3 на звено 4. Реакция
— реакцию, действующую в шарнире С со стороны звена 3 на звено 4. Реакция 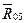 не известна по величине, но известна по направлению — перпендикулярна направляющей х. Реакция
не известна по величине, но известна по направлению — перпендикулярна направляющей х. Реакция 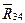 —• неизвестна ни по величине,: ни по направлению. Поэтому разложим ее на две составляющие:
—• неизвестна ни по величине,: ни по направлению. Поэтому разложим ее на две составляющие: 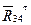 — тангенциальную, направленную перпендикулярно звену СD и
— тангенциальную, направленную перпендикулярно звену СD и 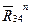 — нормальную, направленную вдоль звена CD (рис. 1.1). Для того, чтобы написать условия равновесия для группы 222, необходимо приложить к ней силы инерции. Величина силы инерции звена 5 определяется по формуле
— нормальную, направленную вдоль звена CD (рис. 1.1). Для того, чтобы написать условия равновесия для группы 222, необходимо приложить к ней силы инерции. Величина силы инерции звена 5 определяется по формуле
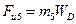
где 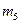 — масса звена 5;
— масса звена 5;
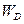 —полное ускорение точки
—полное ускорение точки 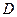 , м/с2;
, м/с2; 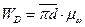

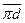 —взято из плана ускорений.
—взято из плана ускорений.
Сила инерции 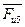 приложена в точке D ползуна 5 и направлена противоположно направлению ускорения
приложена в точке D ползуна 5 и направлена противоположно направлению ускорения 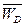 . Сила инерции
. Сила инерции 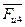 , H звена 4 приложена в центре тяжести
, H звена 4 приложена в центре тяжести 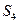 этого звена, направлена противоположно ускорению
этого звена, направлена противоположно ускорению 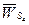 точки
точки 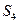 и равна по величине
и равна по величине 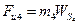 .
.
Центр тяжести 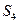 звена 4 находится на расстоянии
звена 4 находится на расстоянии 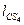 . На основании теоремы подобия точка
. На основании теоремы подобия точка 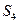 на плане ускорений (рис. 2.1,г) будет лежать на расстоянии
на плане ускорений (рис. 2.1,г) будет лежать на расстоянии 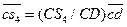 . Соединив точку
. Соединив точку 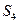 с полюсом
с полюсом 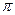 , получим вектор
, получим вектор 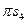 , который будет изображать величину и направление ускорения точки в выбранном масштабе. Величину его, м/с2, находим по формуле
, который будет изображать величину и направление ускорения точки в выбранном масштабе. Величину его, м/с2, находим по формуле
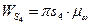
Момент сил инерции, Нм, звена 4 определяется по формуле
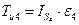
и направлен в сторону, противоположную направлению углового ускорения 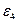 — в нашем случае по часовой стрелке.
— в нашем случае по часовой стрелке.
Момент инерции, кгм2, звена 4 относительно оси, проходящей через центр тяжести, определяем по формуле
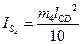
Силу инерции 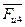 и момент силы инерции
и момент силы инерции 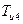 можно привести к одной результирующей силе инерции. Для этого следует момент силы инерции
можно привести к одной результирующей силе инерции. Для этого следует момент силы инерции 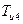 заменить парой сил
заменить парой сил 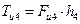
Откуда 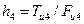 , а отрезок на чертеже, выражающий эту величину в мм,
, а отрезок на чертеже, выражающий эту величину в мм, 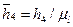 .
.
Силу 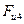 следует переносить так, чтобы она создавала момент относительно точки
следует переносить так, чтобы она создавала момент относительно точки 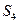 , направленный в ту же сторону, что и
, направленный в ту же сторону, что и 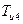 . Точку пересечения линии действия силы
. Точку пересечения линии действия силы 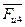 со звеном CD обозначим через
со звеном CD обозначим через 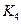 . Определению подлежат реакции
. Определению подлежат реакции 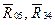 и
и 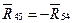 .
.
Рассматривая равновесие звена 4 (рис. 1.1), можно записать, что сумма моментов всех сил, действующих на одно звено, относительно точки D равна нулю, т. е. 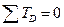 . Перед составлением уравнения зададим направление реакции
. Перед составлением уравнения зададим направление реакции 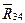 . Тогда
. Тогда
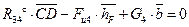
Все плечи определяются непосредственно замером на чертеже в миллиметрах.
Решая уравнение относительно неизвестной силы 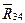 и подставляя числовые значения, получим в Ньютонах.
и подставляя числовые значения, получим в Ньютонах.
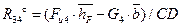
Если искомая сила получилась с положительным знаком, то ее действительное направление совпадает с первоначально выбранным. Если же сила 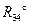 получится со знаком «минус», то это означает, что она направлена противоположно направлению, первоначально выбранному (рис. 1.1). В дальнейших расчетах мы будем принимать ее действительное направление.
получится со знаком «минус», то это означает, что она направлена противоположно направлению, первоначально выбранному (рис. 1.1). В дальнейших расчетах мы будем принимать ее действительное направление.
Теперь рассмотрим равновесие всей группы в целом и определим реакции 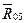 и
и 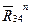 . Поскольку группа находится в равновесии под действием заданных сил, сил реакций и сил инерции, то главный вектор всех сил равен нулю. Составляем уравнение
. Поскольку группа находится в равновесии под действием заданных сил, сил реакций и сил инерции, то главный вектор всех сил равен нулю. Составляем уравнение
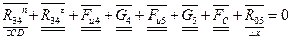
Это означает, что многоугольник сил должен быть, замкнутым. В данном векторном уравнении неизвестными являются величины сил 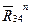 и
и 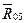 , а направления этих сил известны.
, а направления этих сил известны.
Для наиболее рационального построения плана сил в уравнении, выражающем геометрическую сумму всех сил, векторы рекомендуется записывать в определенном порядке. Во-первых, согласно принципу построения необходимо записывать одну неизвестную силу в начале, а другую — в конце уравнения. Во-вторых, тангенциальную составляющую какой-либо реакции записывать рядом с ее нормальной составляющей. Это позволит сразу на том же плане сил определить полную реакцию. В-тре-тьих, следует сгруппировать все силы, действующие на одно збено (звено 4), а затем на другое (звено 5).
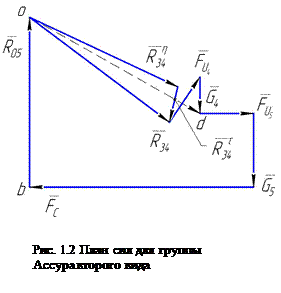 В соответствии с векторным уравнением начинаем строить многоугольник сил, начиная с силы
В соответствии с векторным уравнением начинаем строить многоугольник сил, начиная с силы 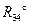 (рис. 1.2), последовательно откладывая векторы сил. Построение ведем в произвольно выбранном масштабе
(рис. 1.2), последовательно откладывая векторы сил. Построение ведем в произвольно выбранном масштабе 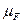 в Н/мм. Чтобы отложить на плане сил векторы, изображающие силы, их величины следуеч разделить на масштаб сил. В конце каждого вектора ставим стрелку и здесь же ставим его обозначение. Построение известных сил заканчивается вектором
в Н/мм. Чтобы отложить на плане сил векторы, изображающие силы, их величины следуеч разделить на масштаб сил. В конце каждого вектора ставим стрелку и здесь же ставим его обозначение. Построение известных сил заканчивается вектором 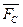 . Чтобы замкнуть многоугольник, проводим через начало силы
. Чтобы замкнуть многоугольник, проводим через начало силы 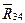 направление силы
направление силы 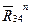 , а через конец силы
, а через конец силы 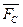 — направление силы
— направление силы 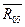 . Эти силы пересекаются в некоторой точке— о и замыкают силовой многоугольник. Точка о пересечения этих сил определяет их величины: отрезок
. Эти силы пересекаются в некоторой точке— о и замыкают силовой многоугольник. Точка о пересечения этих сил определяет их величины: отрезок 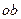 изображает силу
изображает силу 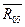 , а отрезок
, а отрезок  — силу
— силу 
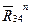 . Определим их истинные величины:
. Определим их истинные величины:
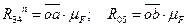
Определив 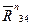 и
и 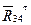 можно сразу же на плане сил на_йти полную реакцию
можно сразу же на плане сил на_йти полную реакцию 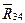 как их равнодействующую:
как их равнодействующую: 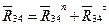
Истинная величина 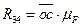
Рассмотрим равновесие звена 4 и определим реакцию 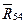 . Поскольку звено 4 находится в равновесии, геометрическая сумма всех сил, действующих на него, равна нулю:
. Поскольку звено 4 находится в равновесии, геометрическая сумма всех сил, действующих на него, равна нулю:
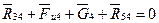
Векторная сумма 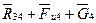 на плане сил уже имеется. Следовательно, если соединим начало вектора
на плане сил уже имеется. Следовательно, если соединим начало вектора 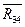 с концом Вектора
с концом Вектора 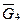 , то получим искомый вектор
, то получим искомый вектор 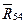 (рис. 1.2). Его истинная величина
(рис. 1.2). Его истинная величина 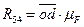
Переходим к расчету группы 221 (звенья 2 и 3). На эту структурную группу действуют следующие силы. В точке С со стороны звена 4 на звено 3 действует сила 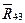 (рис. 1.3). Она равна по величине силе
(рис. 1.3). Она равна по величине силе 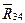 и противоположна ей по направлению.
и противоположна ей по направлению.
В центре тяжести 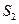 звена 2 приложена сила веса
звена 2 приложена сила веса  . Сила
. Сила 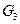 приложена в центре тяжести
приложена в центре тяжести 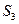 звена 3, расположенном на его середине. В шарнире А со стороны звена 1 на звено 2 действует неизвестная по величине и направлению реакция
звена 3, расположенном на его середине. В шарнире А со стороны звена 1 на звено 2 действует неизвестная по величине и направлению реакция 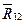 . Разложим ее на две составляющие:
. Разложим ее на две составляющие: 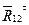 — тангенциальную, направленную перпендикулярно звену АВ, и
— тангенциальную, направленную перпендикулярно звену АВ, и 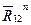 — нормальную, направленную вдоль звена АВ, т.е.
— нормальную, направленную вдоль звена АВ, т.е.
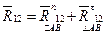
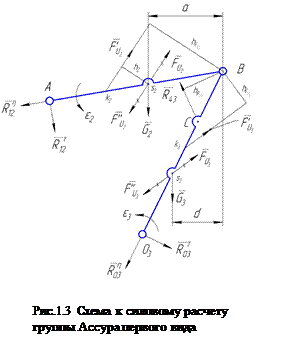 В шарнире 03 со стороны неподвижного звена О (стойки) на звено 3 действует неизвестная по величине и направлению реакция
В шарнире 03 со стороны неподвижного звена О (стойки) на звено 3 действует неизвестная по величине и направлению реакция 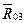 . Ее также разлагаем по двум направлениям:
. Ее также разлагаем по двум направлениям: 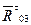 — перпендикулярно звену
— перпендикулярно звену 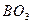 и
и 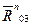 — вдоль звена
— вдоль звена 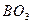 , т. е.
, т. е.
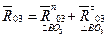
Сила инерции 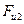 , H, звена 2 приложена в центре тяжести
, H, звена 2 приложена в центре тяжести 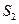 , направлена противоположно ускорению центра тяжести
, направлена противоположно ускорению центра тяжести 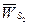
И
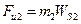
На плане ускорений находим точку 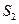 и соединяем ее с полюсом. Полученный отрезок
и соединяем ее с полюсом. Полученный отрезок 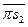 и будет изображать ускорение точки
и будет изображать ускорение точки 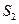 .
.
Момент сил инерции 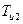 звена, Нм, определяется по формуле
звена, Нм, определяется по формуле
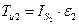
и направлен противоположно угловому ускорению 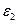 . В нашем случае он направлен по часовой стрелке. Момент инерции, кгм2, относительно оси, проходящей через его центр тяжести
. В нашем случае он направлен по часовой стрелке. Момент инерции, кгм2, относительно оси, проходящей через его центр тяжести 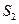 , находится по формуле
, находится по формуле
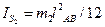
Силу инерции и момент сил инерции 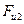 и
и 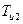 можно привести к одной результирующей силе инерции. Для этого следует момент сил инерции заменить парой сил
можно привести к одной результирующей силе инерции. Для этого следует момент сил инерции заменить парой сил 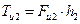 . Откуда
. Откуда 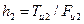 , измеряется в метрах.
, измеряется в метрах.
Отрезок на чертеже, выражающий эту величину, в мм,
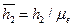
Силы инерции звена 3 можно найти аналогично.
Так как звено 3 вращается вокруг неподвижной оси 03, не проходящей через центр тяжести S3, звена 3, то результирующая сила инерции будет приложена в центре качания (точке 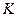 ) звена 3, направлена противоположно ускорению
) звена 3, направлена противоположно ускорению 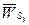 центра тяжести
центра тяжести 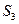 и
и 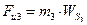
Положение центра качания К, м, определяется по формуле
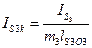
нашем случае 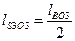 и
и 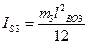 тогда величина
тогда величина 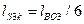 и ее масштабное значение в мм
и ее масштабное значение в мм
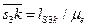
Рассмотрим равновесие звена 2 и определим реакцию 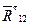 . Для этого составим уравнение моментов всех сил, действующих на звено 2, относительно точки С, предварительно выбрав направление реакции
. Для этого составим уравнение моментов всех сил, действующих на звено 2, относительно точки С, предварительно выбрав направление реакции 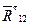 :
:
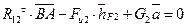
Решая это уравнение относительно 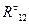 , получим
, получим
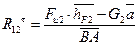
Величины плеч 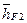 ,
, 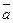 ,
, 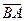 берем с чертежа (рис. 1.3).
берем с чертежа (рис. 1.3).
Если сила 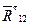 получится со знаком «плюс», то ее действительное направление совпадет с первоначально выбранным, а если со знаком «минус», то действительное направление ее будет противоположно выбранному.
получится со знаком «плюс», то ее действительное направление совпадет с первоначально выбранным, а если со знаком «минус», то действительное направление ее будет противоположно выбранному.
Определим реакцию 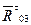 . Для этого составим уравнение моментов всех сил, действующих на звено 3, относительно точки В, предварительно выбрав направление реакции
. Для этого составим уравнение моментов всех сил, действующих на звено 3, относительно точки В, предварительно выбрав направление реакции 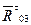 :
:
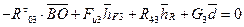
Решая это уравнение относительно 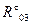 , предварительно замерив плечи на чертеже (рис. 1.3), получим
, предварительно замерив плечи на чертеже (рис. 1.3), получим
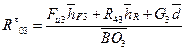
Для определения сил 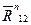 ,
, 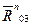 , воспользуемся принципом Даламбера. На основании этого принципа можно записать условие равновесия, согласно которому результирующий вектор всех сил, действующих на группу
, воспользуемся принципом Даламбера. На основании этого принципа можно записать условие равновесия, согласно которому результирующий вектор всех сил, действующих на группу 
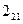 , равен нулю:
, равен нулю:
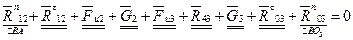
Это означает, что многоугольник сил должен быть замкнутым. В данном векторном уравнении неизвестными являются величины сил 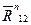 и
и 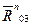 , а направления этих сил известны.
, а направления этих сил известны.
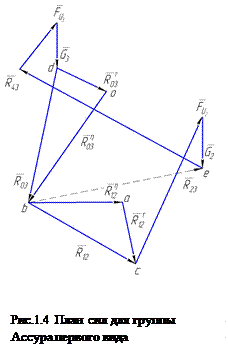
В соответствии с этим уравнением начинаем строить многоугольник сил с известной силы 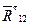 (рис. 1.4), последовательно откладывая векторы сил. Чтобы отложить на плане сил векторы, изображающие силы, следует предварительно их величины разделить на масштаб сил. Последней известной силой будет . Через конец вектора
(рис. 1.4), последовательно откладывая векторы сил. Чтобы отложить на плане сил векторы, изображающие силы, следует предварительно их величины разделить на масштаб сил. Последней известной силой будет . Через конец вектора 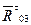 и через начало вектора
и через начало вектора 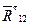 (точка а) проводим линии, параллельные звеньям ВОз и ВА. Эти линии пересекаются в точке b, которая и определит величины векторов
(точка а) проводим линии, параллельные звеньям ВОз и ВА. Эти линии пересекаются в точке b, которая и определит величины векторов 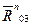 и
и 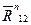 и их направления на чертеже. Определим их истинные величины
и их направления на чертеже. Определим их истинные величины
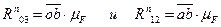
Определим полные реакции 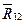 и
и 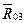 :
:
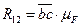 и
и 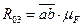
Рассматривая равновесие звена 2 или 3, определяем реакцию 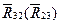
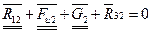
Или
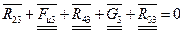
Сумма первых трех векторов по первому уравнению или сумма четырех последних векторов по второму уравнению на плане сил уже построена. Тогда из конца вектора G2 (точка е) проводим прямую в начало вектора 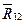 (точка b). Это и есть сила
(точка b). Это и есть сила 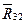 или
или 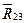 , действующая в кинематической паре В.
, действующая в кинематической паре В.
Истинная величина этой силы 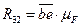
На рис. 1.4 эта сила показана пунктирной линией. Но нужно ПОМНИТЬ, что 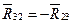
Переходим к кинетостатике ведущего звена. Сила тяжести 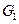 ведущего звена
ведущего звена 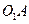 приложена в центре тяжести
приложена в центре тяжести 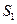 (рис. 1.5).
(рис. 1.5).
В точке А на звено 1 со стороны звена 2 действует сила 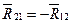
Сила инерции приложена в центре тяжести 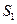 и равна по величине
и равна по величине 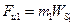
Так как ведущее звено вращается равномерно, считаем, что действующие на него силы уравновешиваются силой, которую назовем уравновешивающей 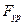 , приложенной к нему со стороны двигателя. Точка приложения и направление уравновешивающей силы зависят от конструкции привода, передающего движение от двигателя к рабочей машине.
, приложенной к нему со стороны двигателя. Точка приложения и направление уравновешивающей силы зависят от конструкции привода, передающего движение от двигателя к рабочей машине.





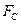 .
.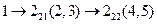 .
.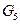 и
и 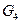 звеньев 5 и 4 приложены в центрах тяжести в точках
звеньев 5 и 4 приложены в центрах тяжести в точках 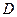 и
и 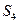 и направлены вертикально вниз. Так как группы Ассура являются статически определимыми кинематическими цепями, то, применяя принцип Даламбера, сводим задачу динамики к задаче статики. Рассматриваемая группа освобождена от связей. Вместо них надо приложить соответствующие реакции:
и направлены вертикально вниз. Так как группы Ассура являются статически определимыми кинематическими цепями, то, применяя принцип Даламбера, сводим задачу динамики к задаче статики. Рассматриваемая группа освобождена от связей. Вместо них надо приложить соответствующие реакции: 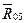 — реакцию, действующую в поступательной паре со стороны стойки на звено 5 и
— реакцию, действующую в поступательной паре со стороны стойки на звено 5 и 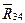 — реакцию, действующую в шарнире С со стороны звена 3 на звено 4. Реакция
— реакцию, действующую в шарнире С со стороны звена 3 на звено 4. Реакция 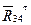 — тангенциальную, направленную перпендикулярно звену СD и
— тангенциальную, направленную перпендикулярно звену СD и 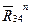 — нормальную, направленную вдоль звена CD (рис. 1.1). Для того, чтобы написать условия равновесия для группы 222, необходимо приложить к ней силы инерции. Величина силы инерции звена 5 определяется по формуле
— нормальную, направленную вдоль звена CD (рис. 1.1). Для того, чтобы написать условия равновесия для группы 222, необходимо приложить к ней силы инерции. Величина силы инерции звена 5 определяется по формуле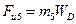
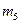 — масса звена 5;
— масса звена 5;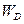 —полное ускорение точки
—полное ускорение точки 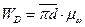

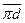 —взято из плана ускорений.
—взято из плана ускорений.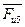 приложена в точке D ползуна 5 и направлена противоположно направлению ускорения
приложена в точке D ползуна 5 и направлена противоположно направлению ускорения 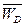 . Сила инерции
. Сила инерции 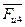 , H звена 4 приложена в центре тяжести
, H звена 4 приложена в центре тяжести 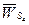 точки
точки 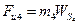 .
.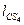 . На основании теоремы подобия точка
. На основании теоремы подобия точка 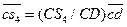 . Соединив точку
. Соединив точку 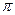 , получим вектор
, получим вектор 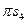 , который будет изображать величину и направление ускорения точки в выбранном масштабе. Величину его, м/с2, находим по формуле
, который будет изображать величину и направление ускорения точки в выбранном масштабе. Величину его, м/с2, находим по формуле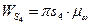
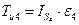
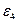 — в нашем случае по часовой стрелке.
— в нашем случае по часовой стрелке.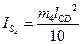
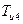 можно привести к одной результирующей силе инерции. Для этого следует момент силы инерции
можно привести к одной результирующей силе инерции. Для этого следует момент силы инерции 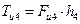
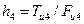 , а отрезок на чертеже, выражающий эту величину в мм,
, а отрезок на чертеже, выражающий эту величину в мм, 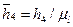 .
.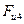 следует переносить так, чтобы она создавала момент относительно точки
следует переносить так, чтобы она создавала момент относительно точки 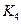 . Определению подлежат реакции
. Определению подлежат реакции 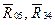 и
и 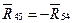 .
.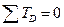 . Перед составлением уравнения зададим направление реакции
. Перед составлением уравнения зададим направление реакции 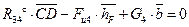
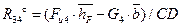
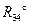 получится со знаком «минус», то это означает, что она направлена противоположно направлению, первоначально выбранному (рис. 1.1). В дальнейших расчетах мы будем принимать ее действительное направление.
получится со знаком «минус», то это означает, что она направлена противоположно направлению, первоначально выбранному (рис. 1.1). В дальнейших расчетах мы будем принимать ее действительное направление.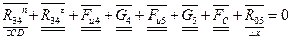
 В соответствии с векторным уравнением начинаем строить многоугольник сил, начиная с силы
В соответствии с векторным уравнением начинаем строить многоугольник сил, начиная с силы 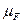 в Н/мм. Чтобы отложить на плане сил векторы, изображающие силы, их величины следуеч разделить на масштаб сил. В конце каждого вектора ставим стрелку и здесь же ставим его обозначение. Построение известных сил заканчивается вектором
в Н/мм. Чтобы отложить на плане сил векторы, изображающие силы, их величины следуеч разделить на масштаб сил. В конце каждого вектора ставим стрелку и здесь же ставим его обозначение. Построение известных сил заканчивается вектором 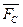 . Чтобы замкнуть многоугольник, проводим через начало силы
. Чтобы замкнуть многоугольник, проводим через начало силы 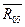 . Эти силы пересекаются в некоторой точке— о и замыкают силовой многоугольник. Точка о пересечения этих сил определяет их величины: отрезок
. Эти силы пересекаются в некоторой точке— о и замыкают силовой многоугольник. Точка о пересечения этих сил определяет их величины: отрезок 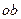 изображает силу
изображает силу  — силу
— силу 
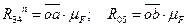
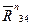 и
и 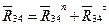
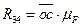
 . Поскольку звено 4 находится в равновесии, геометрическая сумма всех сил, действующих на него, равна нулю:
. Поскольку звено 4 находится в равновесии, геометрическая сумма всех сил, действующих на него, равна нулю: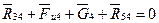
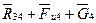 на плане сил уже имеется. Следовательно, если соединим начало вектора
на плане сил уже имеется. Следовательно, если соединим начало вектора 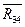 с концом Вектора
с концом Вектора 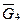 , то получим искомый вектор
, то получим искомый вектор 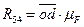
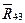 (рис. 1.3). Она равна по величине силе
(рис. 1.3). Она равна по величине силе 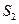 звена 2 приложена сила веса
звена 2 приложена сила веса  . Сила
. Сила 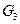 приложена в центре тяжести
приложена в центре тяжести 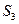 звена 3, расположенном на его середине. В шарнире А со стороны звена 1 на звено 2 действует неизвестная по величине и направлению реакция
звена 3, расположенном на его середине. В шарнире А со стороны звена 1 на звено 2 действует неизвестная по величине и направлению реакция 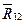 . Разложим ее на две составляющие:
. Разложим ее на две составляющие: 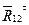 — тангенциальную, направленную перпендикулярно звену АВ, и
— тангенциальную, направленную перпендикулярно звену АВ, и 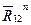 — нормальную, направленную вдоль звена АВ, т.е.
— нормальную, направленную вдоль звена АВ, т.е.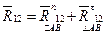
 В шарнире 03 со стороны неподвижного звена О (стойки) на звено 3 действует неизвестная по величине и направлению реакция
В шарнире 03 со стороны неподвижного звена О (стойки) на звено 3 действует неизвестная по величине и направлению реакция 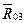 . Ее также разлагаем по двум направлениям:
. Ее также разлагаем по двум направлениям: 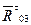 — перпендикулярно звену
— перпендикулярно звену 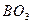 и
и 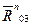 — вдоль звена
— вдоль звена 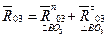
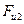 , H, звена 2 приложена в центре тяжести
, H, звена 2 приложена в центре тяжести 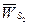
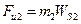
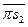 и будет изображать ускорение точки
и будет изображать ускорение точки 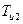 звена, Нм, определяется по формуле
звена, Нм, определяется по формуле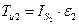
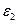 . В нашем случае он направлен по часовой стрелке. Момент инерции, кгм2, относительно оси, проходящей через его центр тяжести
. В нашем случае он направлен по часовой стрелке. Момент инерции, кгм2, относительно оси, проходящей через его центр тяжести 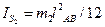
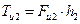 . Откуда
. Откуда 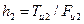 , измеряется в метрах.
, измеряется в метрах.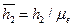
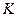 ) звена 3, направлена противоположно ускорению
) звена 3, направлена противоположно ускорению 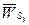 центра тяжести
центра тяжести 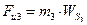
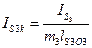
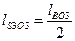 и
и 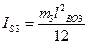 тогда величина
тогда величина 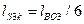 и ее масштабное значение в мм
и ее масштабное значение в мм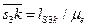
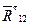 . Для этого составим уравнение моментов всех сил, действующих на звено 2, относительно точки С, предварительно выбрав направление реакции
. Для этого составим уравнение моментов всех сил, действующих на звено 2, относительно точки С, предварительно выбрав направление реакции 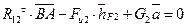
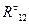 , получим
, получим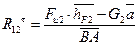
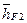 ,
, 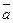 ,
, 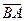 берем с чертежа (рис. 1.3).
берем с чертежа (рис. 1.3).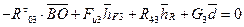
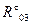 , предварительно замерив плечи на чертеже (рис. 1.3), получим
, предварительно замерив плечи на чертеже (рис. 1.3), получим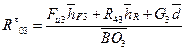
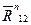 ,
, 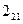 , равен нулю:
, равен нулю:
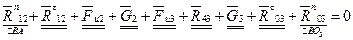
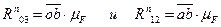
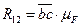 и
и 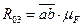
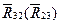
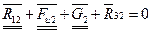
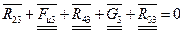
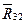 или
или 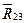 , действующая в кинематической паре В.
, действующая в кинематической паре В.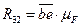
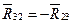
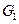 ведущего звена
ведущего звена 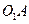 приложена в центре тяжести
приложена в центре тяжести 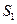 (рис. 1.5).
(рис. 1.5).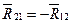
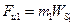
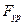 , приложенной к нему со стороны двигателя. Точка приложения и направление уравновешивающей силы зависят от конструкции привода, передающего движение от двигателя к рабочей машине.
, приложенной к нему со стороны двигателя. Точка приложения и направление уравновешивающей силы зависят от конструкции привода, передающего движение от двигателя к рабочей машине.


