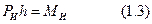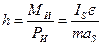Внешние силы
Задачей силового исследования механизмов является определение реакций в кинематических парах механизма, находящегося под действием заданных внешних сил. Закон движения механизма (ведущего звена) при этом считается заданным.
 Силовое исследование механизмов имеет очень важное значение, так как найденные реакции являются необходимыми для расчета звеньев и элементов кинематических пар на прочность, износостойкость, долговечность и т. д.
Силовое исследование механизмов имеет очень важное значение, так как найденные реакции являются необходимыми для расчета звеньев и элементов кинематических пар на прочность, износостойкость, долговечность и т. д.
Все внешние силы, действующие на машину, можно разбить на две большие группы: силы движущие Рд (и моменты движущих сил МД) и силы сопротивления Рс (и моменты сил сопротивления Мс).
Движущими силами называются такие силы, которые совершают положительную работу. Эти силы направлены в сторону движения (в сторону скорости) точки приложения силы или составляют с этим направлением острый угол. Движущие силы стремятся ускорить движение.
Силами сопротивления называются такие силы, которые совершают отрицательную работу. Эти силы направлены противоположно направлению движения (скорости) точки приложения или составляют с этим направлением тупой угол. Силы сопротивления стремятся замедлить движение (рис. 1.1, а).
Аналогично моменты движущих сил Мл направлены в сторону вращения (в сторону угловой скорости) звена, а моменты сил сопротивления Мс направлены противоположно движению (рис. 1. 1,б). Силы сопротивления в свою очередь делятся на силы полезных, или технологических, сопротивлений и силы вредных сопротивлений.
Силами полезных (технологических) сопротивлений называются такие силы, которые совершают работу, требуемую от механизма.
Силами вредных сопротивлений являются в основном силы трения. Эти силы всегда имеют место при относительном перемещении соприкасающихся звеньев.
При проектировании машины, конечно, всегда следует стремиться уменьшить и силы полезных и силы вредных сопротивлений. При работе всякой машины на нее всегда действуют и силы движущие и силы различных сопротивлений. Например, в лесопильной раме движущими силами является движущий момент МД, развиваемый двигателем, приводящим в движение лесопильную раму. Силами полезных сопротивлений являются силы сопротивления резанию Ррез древесины (лесопильная рама для того и создана, чтобы преодолевать эти силы), Силами вредных сопротивлений являются силы трения между рамой и направляющими, в различных шарнирах (подшипниках) и т. д.
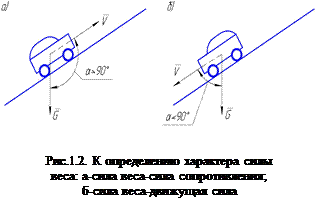 К внешним силам относятся также силы веса звеньев, которые могут быть силами движущими и силами сопротивления. Они являются силами движущими, когда центр тяжести звена опускается (в этом случае направление силы веса составляет с направлением скорости центра тяжести звена острый угол), или силами сопротивления, когда центр тяжести звена подымается (в этом случае направление силы веса составляет с направлением скорости центра тяжести звена тупой угол). Наглядно это видно на примере движения автомашины. Когда автомашина подымается в гору (рис. 1.2, а), сила веса является силой сопротивления. Когда машина спускается с горы (рис. 1.2, б), сила ее веса является движущей силой.
К внешним силам относятся также силы веса звеньев, которые могут быть силами движущими и силами сопротивления. Они являются силами движущими, когда центр тяжести звена опускается (в этом случае направление силы веса составляет с направлением скорости центра тяжести звена острый угол), или силами сопротивления, когда центр тяжести звена подымается (в этом случае направление силы веса составляет с направлением скорости центра тяжести звена тупой угол). Наглядно это видно на примере движения автомашины. Когда автомашина подымается в гору (рис. 1.2, а), сила веса является силой сопротивления. Когда машина спускается с горы (рис. 1.2, б), сила ее веса является движущей силой.
Внешние силы в зависимости от того, в какой машине они действуют, могут быть постоянными или переменными. Во многих машинах они изменяются с изменением положения механизма (например, давление газов на поршень двигателя внутреннего сгорания), в некоторых они зависят от скорости (например, крутящий момент электродвигателя). Силы веса всегда являются постоянными силами.
Все внешние силы при силовом расчете должны быть известны. Поэтому они считаются заданными силами.
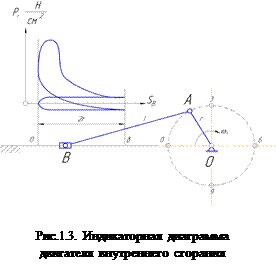
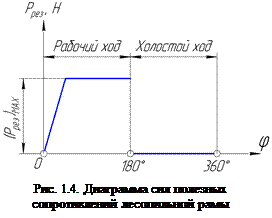
Если внешняя сила является переменной, то она обычно задается диаграммой. Например, на рис. 1.3 показаны индикаторная диаграмма четырехтактного двигателя, по которой видно, как изменяется давление газов на поршень в зависимости от положения последнего. На рис. 1.4 приведен пример изменения силы резания вертикальной лесопильной рамы в зависимости от угла поворота кривошипа. По заданным диаграммам легко определить величины внешних сил для того или иного положения механизма.
Силы инерции
Силовой расчет механизма основывается на принципе Даламбера, который заключается в следующем. Во время работы механизма его звенья в общем случае двигаются с ускорением, в результате чего, как известно, возникают силы инерции. Если условно приложить силы инерции к звеньям, то сумма всех сил, включая и силы инерции, приложенных к звеньям, равна нулю. Это позволяет к движущейся системе применить уравнения статики. Поэтому силовой расчет механизмов часто называют кинетостатическим расчетом или просто кинетостатикой механизмов.
Учет сил инерции особенно важен в современных быстроходных машинах, где они достигают больших величин.
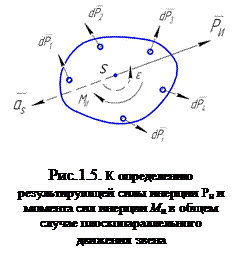 Перейдем к определению сил инерции для различных случаев движения звеньев. Напомним положения, известные из курса теоретической механики.
Перейдем к определению сил инерции для различных случаев движения звеньев. Напомним положения, известные из курса теоретической механики.
В общем случае плоскопараллельного движения звена ускорения его различных материальных точек различны (по величине и направлению). Поэтому различны и элементарные силы инерции 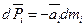 , условно приложенные в этих точках (рис. 1.5). Эта система элементарных сил сводится к одной силе инерции
, условно приложенные в этих точках (рис. 1.5). Эта система элементарных сил сводится к одной силе инерции 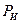 и к одной паре сил инерции с моментом
и к одной паре сил инерции с моментом 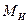 которые равны:
которые равны:
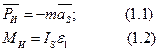
где 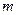 — масса звена;
— масса звена;
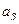 — ускорение центра тяжести звена;
— ускорение центра тяжести звена;
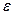 — угловое ускорение звена;
— угловое ускорение звена;
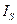 — момент инерции звена относительно оси, проходящей через центр тяжести.
— момент инерции звена относительно оси, проходящей через центр тяжести.
Напомним, что момент инерции звена есть мера инертности звена во вращательном движении. Его величина зависит только от самого тела: от его массы и распределения массы (размеров и формы тела). Момент инерции звена в общем случае определяется формулой
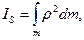
Где 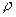 — расстояние каждой элементарной массы от оси, проходящей через центр тяжести S.
— расстояние каждой элементарной массы от оси, проходящей через центр тяжести S.
Интеграл следует брать по всей массе звена т.
 Сила инерции
Сила инерции 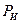 приложена в центре тяжести звена S и направлена противоположно вектору ускорения центра тяжести
приложена в центре тяжести звена S и направлена противоположно вектору ускорения центра тяжести 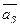 .
.
Момент пары сил инерции направлен противоположно угловому ускорению звена 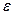 (это показывают знаки «минус»).
(это показывают знаки «минус»).
Рассмотрим, к чему сводятся силы инерции при различных случаях движения звена.
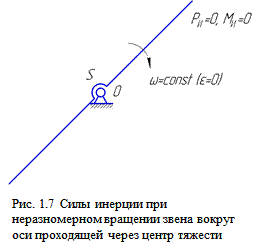
1. Поступательное движение звена (рис. 1.6), При поступательном движении звена ускорения всех точек одинаковы, поэтому силу инерции можно выразить через ускорение любой точки звена:
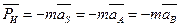
Приложена сила инерции в центре тяжести. Момент сил инерции звена Ми=0, так как при поступательном движении звена оно не имеет углового ускорения 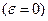 .
.
2. Звено неравномерно 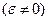 вращается вокруг оси, проходящей через центр тяжести (рис. 1.7). Сила инерции в этом случае равна
вращается вокруг оси, проходящей через центр тяжести (рис. 1.7). Сила инерции в этом случае равна 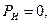 так как ускорение центра тяжести
так как ускорение центра тяжести 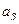 =0. Момент сил инерции равен
=0. Момент сил инерции равен 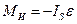 и направлен противоположно угловому ускорению
и направлен противоположно угловому ускорению 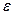 .
.
 3. Звено равномерно
3. Звено равномерно  вращается вокруг оси, не проходящей через центр тяжести (рис. 1.8). В этом случае сила инерции
вращается вокруг оси, не проходящей через центр тяжести (рис. 1.8). В этом случае сила инерции 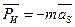 , где
, где 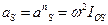 . Направлена сила инерции противоположно ускорению центра тяжести, т. е. вдоль радиуса
. Направлена сила инерции противоположно ускорению центра тяжести, т. е. вдоль радиуса 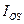 от центра О.
от центра О.
Момент сил инерции 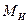 =0, так как угловое ускорение
=0, так как угловое ускорение 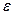 =0.
=0.
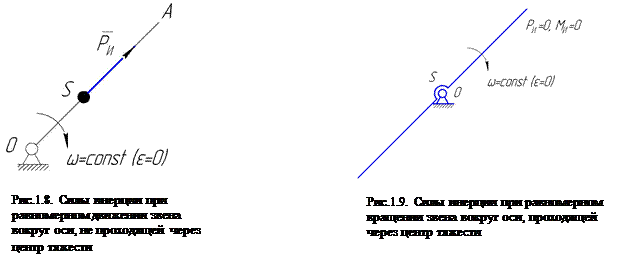
4. Звено равномерно ( 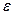 =0) вращается вокруг оси, проходящей через центр тяжести (рис. 1.9). В этом случае сила инерции
=0) вращается вокруг оси, проходящей через центр тяжести (рис. 1.9). В этом случае сила инерции 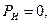 (так как as = 0) и момент сил инерции
(так как as = 0) и момент сил инерции 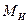 =0
=0
(так как 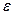 =0).Такое звено называется уравновешенным.
=0).Такое звено называется уравновешенным.
5. Звено неравномерно 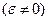 вращается вокруг оси, не проходящей через центр тяжести (рис. 1.10).
вращается вокруг оси, не проходящей через центр тяжести (рис. 1.10).
 В этом случае возникает и сила инерции и момент сил инерции:
В этом случае возникает и сила инерции и момент сил инерции:
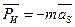
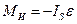
где 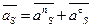 ; по величине
; по величине 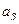 равно
равно 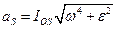 . Сила инерции
. Сила инерции  приложена в центре тяжести и направлена противоположно ускорению центра тяжести
приложена в центре тяжести и направлена противоположно ускорению центра тяжести 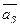 . Момент пары сил инерции
. Момент пары сил инерции 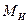 направлен противоположно угловому ускорению
направлен противоположно угловому ускорению 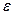 (рис. 1.10, а).
(рис. 1.10, а).
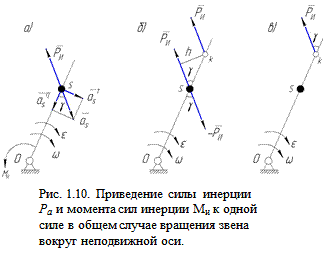
Часто удобно силу инерции 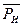 и момент сил инерции
и момент сил инерции 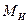 привести к одной равнодействующей силе
привести к одной равнодействующей силе 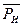 . Для этого заменим момент
. Для этого заменим момент 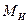 парой сил
парой сил 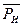 и
и 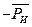 , момент которой равен
, момент которой равен
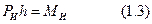
Силу 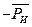 этой пары приложим в центре тяжести S. Тогда другая сила
этой пары приложим в центре тяжести S. Тогда другая сила 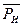 окажется приложенной в некоторой точке К звена (рис. 1.10,б). Силы
окажется приложенной в некоторой точке К звена (рис. 1.10,б). Силы 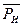 и
и 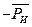 , приложенные в центра тяжести, взаимно уравновешиваются, и, таким образом, остается только одна сила, приложенная в точке К звена (рис. 1.10, в). Эта точка называется точкой качания.
, приложенные в центра тяжести, взаимно уравновешиваются, и, таким образом, остается только одна сила, приложенная в точке К звена (рис. 1.10, в). Эта точка называется точкой качания.
Таким образом, силу инерции 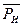 , приложенную в центре тяжести S, и момент сил инерции
, приложенную в центре тяжести S, и момент сил инерции 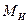 можно заменить одной силой
можно заменить одной силой 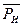 , которая приложена в точке качания K. Момент сил инерции при этом автоматически учитывается.
, которая приложена в точке качания K. Момент сил инерции при этом автоматически учитывается.
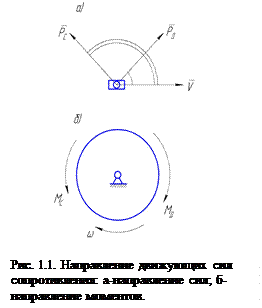
Определим положение точки качания. Из уравнения (1.3) получаем, что плечо пары сил h равно
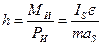





 Силовое исследование механизмов имеет очень важное значение, так как найденные реакции являются необходимыми для расчета звеньев и элементов кинематических пар на прочность, износостойкость, долговечность и т. д.
Силовое исследование механизмов имеет очень важное значение, так как найденные реакции являются необходимыми для расчета звеньев и элементов кинематических пар на прочность, износостойкость, долговечность и т. д. К внешним силам относятся также силы веса звеньев, которые могут быть силами движущими и силами сопротивления. Они являются силами движущими, когда центр тяжести звена опускается (в этом случае направление силы веса составляет с направлением скорости центра тяжести звена острый угол), или силами сопротивления, когда центр тяжести звена подымается (в этом случае направление силы веса составляет с направлением скорости центра тяжести звена тупой угол). Наглядно это видно на примере движения автомашины. Когда автомашина подымается в гору (рис. 1.2, а), сила веса является силой сопротивления. Когда машина спускается с горы (рис. 1.2, б), сила ее веса является движущей силой.
К внешним силам относятся также силы веса звеньев, которые могут быть силами движущими и силами сопротивления. Они являются силами движущими, когда центр тяжести звена опускается (в этом случае направление силы веса составляет с направлением скорости центра тяжести звена острый угол), или силами сопротивления, когда центр тяжести звена подымается (в этом случае направление силы веса составляет с направлением скорости центра тяжести звена тупой угол). Наглядно это видно на примере движения автомашины. Когда автомашина подымается в гору (рис. 1.2, а), сила веса является силой сопротивления. Когда машина спускается с горы (рис. 1.2, б), сила ее веса является движущей силой.

 Перейдем к определению сил инерции для различных случаев движения звеньев. Напомним положения, известные из курса теоретической механики.
Перейдем к определению сил инерции для различных случаев движения звеньев. Напомним положения, известные из курса теоретической механики.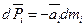 , условно приложенные в этих точках (рис. 1.5). Эта система элементарных сил сводится к одной силе инерции
, условно приложенные в этих точках (рис. 1.5). Эта система элементарных сил сводится к одной силе инерции 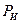 и к одной паре сил инерции с моментом
и к одной паре сил инерции с моментом 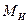 которые равны:
которые равны: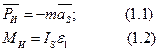
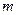 — масса звена;
— масса звена;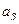 — ускорение центра тяжести звена;
— ускорение центра тяжести звена;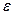 — угловое ускорение звена;
— угловое ускорение звена;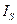 — момент инерции звена относительно оси, проходящей через центр тяжести.
— момент инерции звена относительно оси, проходящей через центр тяжести.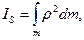
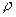 — расстояние каждой элементарной массы от оси, проходящей через центр тяжести S.
— расстояние каждой элементарной массы от оси, проходящей через центр тяжести S.
 Сила инерции
Сила инерции 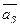 .
.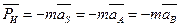
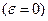 .
.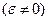 вращается вокруг оси, проходящей через центр тяжести (рис. 1.7). Сила инерции в этом случае равна
вращается вокруг оси, проходящей через центр тяжести (рис. 1.7). Сила инерции в этом случае равна 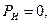 так как ускорение центра тяжести
так как ускорение центра тяжести 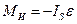 и направлен противоположно угловому ускорению
и направлен противоположно угловому ускорению  3. Звено равномерно
3. Звено равномерно 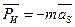 , где
, где 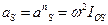 . Направлена сила инерции противоположно ускорению центра тяжести, т. е. вдоль радиуса
. Направлена сила инерции противоположно ускорению центра тяжести, т. е. вдоль радиуса 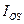 от центра О.
от центра О. В этом случае возникает и сила инерции и момент сил инерции:
В этом случае возникает и сила инерции и момент сил инерции: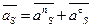 ; по величине
; по величине 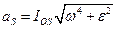 . Сила инерции
. Сила инерции 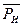 и момент сил инерции
и момент сил инерции 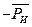 , момент которой равен
, момент которой равен