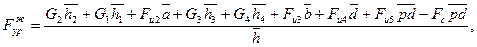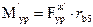
Если вращение передается с помощью зубчатых колес и ступень, которая связана с ведущим звеном, является ступенью с неподвижными осями, то сила 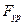 проходит через полюс зацепления, т. е. через точку касания начальных окружностей. Сила
проходит через полюс зацепления, т. е. через точку касания начальных окружностей. Сила 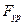 направлена по линии зацепления. При эвольвентном зацеплении линия зацепления совпадает с нормалью, проведенной в точке касания зубьев, и образует с касательной к начальным окружностям угол зацепления
направлена по линии зацепления. При эвольвентном зацеплении линия зацепления совпадает с нормалью, проведенной в точке касания зубьев, и образует с касательной к начальным окружностям угол зацепления 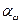 .
.
Сила 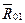 (реакция со стороны стойки О на звено 1 в кинематической паре
(реакция со стороны стойки О на звено 1 в кинематической паре 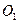 ) неизвестна ни по величине, ни по направлению. Начальные окружности зубчатых колес вычерчиваются в том же масштабе, что и механизм.
) неизвестна ни по величине, ни по направлению. Начальные окружности зубчатых колес вычерчиваются в том же масштабе, что и механизм.
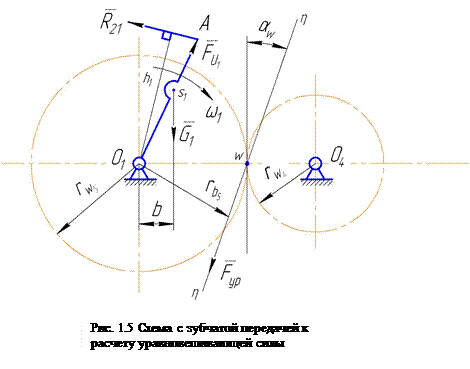
Под действием указанных выше сил можно считать, что ведущее звено 1 находится в равновесии. Поэтому можно применить условие равновесия статики. Для определения величины силы 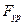 составим уравнение равновесия в виде суммы моментов всех сил, действующих на ведущее звено (кривошип) относительно точки
составим уравнение равновесия в виде суммы моментов всех сил, действующих на ведущее звено (кривошип) относительно точки 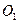 (рис. 1.5);
(рис. 1.5);
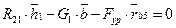
откуда 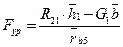
Величины плеч определяются непосредственно из чертежа в миллиметрах. Кратчайшее расстояние (плечо) от точки 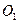 до направления силы
до направления силы 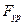 есть не что иное, как радиус основной окружности зубчатого колеса, жестко соединенного со звеном
есть не что иное, как радиус основной окружности зубчатого колеса, жестко соединенного со звеном
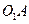
Для определения реакции 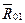 составим уравнение равновесия, согласно которому главный вектор всех сил, действующих на кривошип, равен нулю:
составим уравнение равновесия, согласно которому главный вектор всех сил, действующих на кривошип, равен нулю:
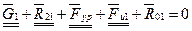
В соответствии с этим уравнением строим план сил, действующих на кривошип (рис. 1.6).
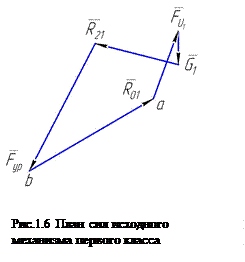
Построение плана начинаем с силы 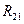 . Сложив все известные силы и соединив точки а и b, получим вектор силы
. Сложив все известные силы и соединив точки а и b, получим вектор силы 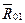 . Его истинная величина
. Его истинная величина 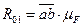 . Сила
. Сила 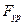 создает на звене
создает на звене 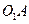 относительно
относительно 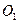 момент, Нм.
момент, Нм.
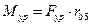
Где 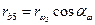
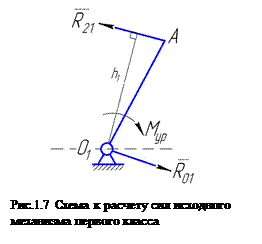
При определении реакции в опоре 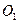 ведущего звена практически возможен и другой случай, когда кривошипный вал соединен с двигателем посредством муфты или жестко связан с водилом или с одним из центральных колес планетарного редуктора (рис. 1.7). В этом случае к валу приложен уравновешивающий момент
ведущего звена практически возможен и другой случай, когда кривошипный вал соединен с двигателем посредством муфты или жестко связан с водилом или с одним из центральных колес планетарного редуктора (рис. 1.7). В этом случае к валу приложен уравновешивающий момент
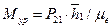
а реакция в опоре вала будет равна действию второго звена на кривошип 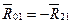 (если пренебречь весом звена 1).
(если пренебречь весом звена 1).
Рассмотрим определение потерь на трение в рычажных механизмах. После того, как рассчитаны давления (реакции) в кинематических парах рычажного механизма с идеальными связями, можно подсчитать суммарную мощность потерь па трение.
Полная мгновенная мощность потерь на трение в механизме получится суммированием мощностей, вычисленных для всех кинематических пар:
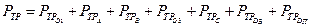
Где 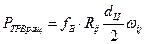
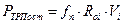
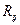 - давление в кинематической паре;
- давление в кинематической паре;
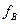 и
и 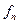 - коэффициенты трения во вращательной и поступательной парах;
- коэффициенты трения во вращательной и поступательной парах;
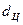 - диаметр шарнира, м;
- диаметр шарнира, м;
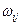 - относительная угловая скорость. Для пары звеньев 1-2
- относительная угловая скорость. Для пары звеньев 1-2 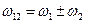 .
.
Знак «плюс» берется, если угловые скорости разного знака, а знак «минус» — если одного знака.
Давления и угловые скорости звеньев были определены выше.
Приведенный к валу момент трения, Нм
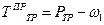
В разных положениях рычажного механизма результат вычислений будет различным, поэтому полная картина получится при рассмотрении ряда положений механизма.
Мгновенный коэффициент полезного действия рычажного механизма определяется по формулам
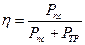 для рабочей машины
для рабочей машины
И
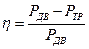 для двигателей,
для двигателей,
Где 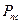 - мощность сил полезного сопротивления;
- мощность сил полезного сопротивления;
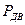 - мощность движущих сил.
- мощность движущих сил.
Мгновенный коэффициент полезного действия рычажного механизма можно также вычислить, если известны приведенный момент трения 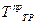 и уравновешивающий момент
и уравновешивающий момент 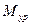 , по формуле
, по формуле
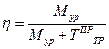
Вычислив этот коэффициент для нескольких положений, можно найти средний коэффициент полезного действия рассматриваемого механизма.
Теорема Н. Е. Жуковского о «жестком рычаге (изучить самостоятельно)
Уравновешивающая сила или уравновешивающий момент могут быть легко определены при помощи теоремы Н. Е. Жуковского о «жестком рычаге».
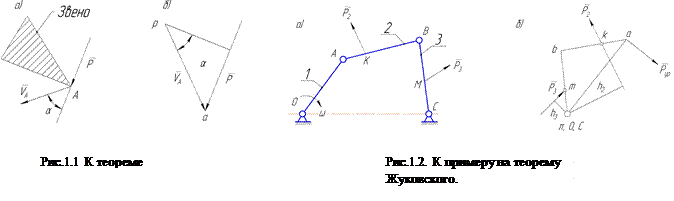 Пусть на точку А какого-либо звена, движущуюся со скорость
Пусть на точку А какого-либо звена, движущуюся со скорость 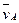 действует сила
действует сила 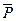 (рис. 1.1, а).
(рис. 1.1, а).
Элементарная работа силы 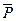 равна
равна
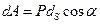
а мгновенная мощность этой силы равна
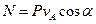 ,
,
где 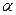 — угол между направлением силы
— угол между направлением силы 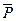 и направлением вектора скорости
и направлением вектора скорости 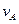 .
.
Повернем вектор скорости 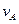 на 90° (в любом направлении) и ггеренееем силу
на 90° (в любом направлении) и ггеренееем силу 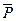 параллельно самой себе в конец этого вектора (в точку а) (рис. 1.1,б). Момент силы
параллельно самой себе в конец этого вектора (в точку а) (рис. 1.1,б). Момент силы 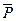 относительно начала вектора
относительно начала вектора 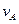 (точки р), как это видно из рисунка, равен
(точки р), как это видно из рисунка, равен
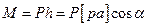
Сравнивая равенства, видим, что момент силы, действующей на некоторую точку (точку А) звена, перенесенной параллельно самой себе в одноименную точку (точку а) повернутого на 90° плана скоростей этой точки, относительно полюса плана, пропорционален мощности этой силы.
Это справедливо для любой силы.
Из теоретической механики известно, что если система (механизм) под действием сил находится в равновесии, то сумма элементарных работ или мощностей этих сил равна нулю. Следовательно, равна нулю и сумма моментов сил относительно полюса повернутого плана скоростей (так как моменты пропорциональны силам).
Если механизм не находится в равновесии, то, приложив силы инерции и уравновешивающую силу (или уравновешивающий момент), можно рассматривать его находящимся в равновесии. Следовательно, сумма моментов всех сил, действующих на механизм, включая и силы инерции, перенесенных параллельно самим себе в одно-именные точки повернутого на 90° плана скоростей, относительно полюса плана, равна нулю.
Таким образом, план скоростей рассматривается как жесткий рычаг, шарнирно закрепленный в полюсе и находящийся под действием сил в равновесии. Эта теорема носит имя ее автора Н. Е. Жуковского и называется теоремой о «жестком рычаге».
По теореме Жуковского легко можно определить уравновешивающую силу Рур или уравновешивающий момент Мур, не определяя реакций в кинематических парах механизма.
Рассмотрим пример. Пусть требуется определить уравновешивающую силу Рур для механизма, на звенья 2 и 3 которого действуют силы Р2 и Р3 (включающие и силы инерции). Уравновешивающая сила приложена в точке А и направлена перпендикулярно кривошипу (рис. 1.2, а).
Решение ведем в такой последовательности.
1. Строим в произвольном масштабе повернутый план скоростей механизма. Некоторые при этом строят сначала обычный план скоростей, затем поворачивают его на 90° — это усложняет построение. Поэтому рекомендуется строить сразу повернутый план скоростей.
План скоростей строим по векторному уравнению
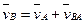
В действительности векторы скоростей в этом уравнении направлены следующим образом:
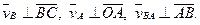
Строя повернутый план скоростей, следует направить эти векторы не перпендикулярно соответствующим звеньям, а параллельно:
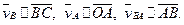
Повернутый план скоростей построен, на рис. 1.2.б.
2. По теореме подобия находим на плане скоростей точки k и т — точки, одноименные точкам К и М механизма, в которых приложены силы 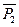 и
и 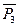 .
.
3. Переносим параллельно самим себе в точки кит соответственно силы 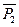 и
и 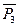 - В точке а плана скоростей перпендикулярно кривошипу ОА (так задано) или перпендикулярно отрезку \ра\ плана скоростей прикладываем уравновешивающую силу Рур,
- В точке а плана скоростей перпендикулярно кривошипу ОА (так задано) или перпендикулярно отрезку \ра\ плана скоростей прикладываем уравновешивающую силу Рур,
Составляем уравнение моментов сил относительно полюса р плана скоростей:
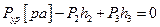 ,
,
Откуда, 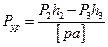
 Отрезки (плечи сил)
Отрезки (плечи сил) 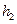 ,
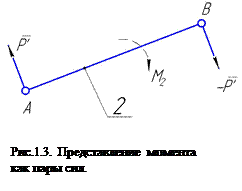
, 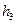 измеряются по чертежу (мм). Если на звенья действуют моменты, то их следует представить как пару сил, вычислив их величины и приложив в соответствующих точках. Например, если на звено 2 действует момент М2, то его представляем как пару сил
измеряются по чертежу (мм). Если на звенья действуют моменты, то их следует представить как пару сил, вычислив их величины и приложив в соответствующих точках. Например, если на звено 2 действует момент М2, то его представляем как пару сил 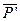 и
и 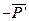 приложенных в точках А и В (рис, 1.3). Величины этих сил определяем по формуле
приложенных в точках А и В (рис, 1.3). Величины этих сил определяем по формуле
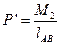
Аналогично следует поступить, если задано, что на ведущее звено действует уравновешивающий момент Мур. Его тогда следует представить как пару сил, приложенных в точках О и A.
Рассмотрим примеры
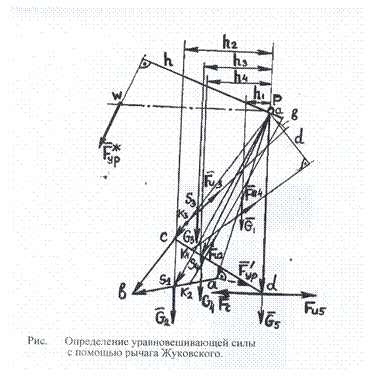
Силу F`ур будем считать условно приложенной в точке А кривошипа перпендикулярно звену О1 А. Тогда на повернутом плане скоростей (рис. ) силу F`ур приложим в точке а перпендикулярно отрезку ра. Затем напишем уравнение моментов всех сил относительно полюса р плана скоростей:

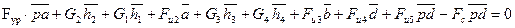
Длину плеч в миллиметрах берем с чертежа (рис. ) Решая составленное уравнение относительно F`ур, получим
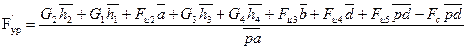
а уравновешивающий момент:
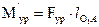
В действительности уравновешивающая сила будет приложена в полюсе зацепления колес 4 и 5. Поэтому желательно на повернутом плане скоростей
определить скорость 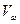 точки зацепления
точки зацепления 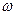 и в конце вектора скорости
и в конце вектора скорости 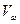 приложить
приложить 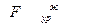 (рис. ). Тогда
(рис. ). Тогда
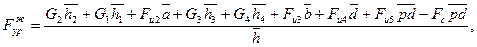
а уравновешивающий момент:
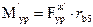






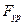 проходит через полюс зацепления, т. е. через точку касания начальных окружностей. Сила
проходит через полюс зацепления, т. е. через точку касания начальных окружностей. Сила 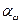 .
.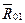 (реакция со стороны стойки О на звено 1 в кинематической паре
(реакция со стороны стойки О на звено 1 в кинематической паре 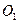 ) неизвестна ни по величине, ни по направлению. Начальные окружности зубчатых колес вычерчиваются в том же масштабе, что и механизм.
) неизвестна ни по величине, ни по направлению. Начальные окружности зубчатых колес вычерчиваются в том же масштабе, что и механизм.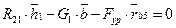
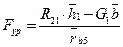
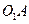
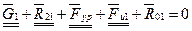


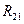 . Сложив все известные силы и соединив точки а и b, получим вектор силы
. Сложив все известные силы и соединив точки а и b, получим вектор силы 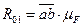 . Сила
. Сила 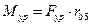
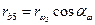
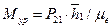
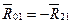 (если пренебречь весом звена 1).
(если пренебречь весом звена 1).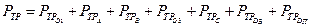
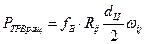
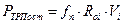
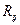 - давление в кинематической паре;
- давление в кинематической паре;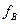 и
и 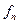 - коэффициенты трения во вращательной и поступательной парах;
- коэффициенты трения во вращательной и поступательной парах;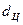 - диаметр шарнира, м;
- диаметр шарнира, м;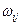 - относительная угловая скорость. Для пары звеньев 1-2
- относительная угловая скорость. Для пары звеньев 1-2 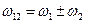 .
.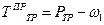
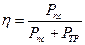 для рабочей машины
для рабочей машины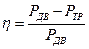 для двигателей,
для двигателей,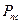 - мощность сил полезного сопротивления;
- мощность сил полезного сопротивления;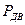 - мощность движущих сил.
- мощность движущих сил.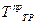 и уравновешивающий момент
и уравновешивающий момент 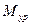 , по формуле
, по формуле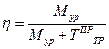
 Пусть на точку А какого-либо звена, движущуюся со скорость
Пусть на точку А какого-либо звена, движущуюся со скорость 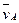 действует сила
действует сила 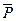 (рис. 1.1, а).
(рис. 1.1, а).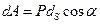
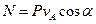 ,
,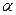 — угол между направлением силы
— угол между направлением силы 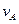 .
.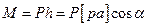
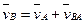
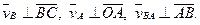
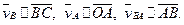
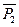 и
и 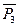 .
.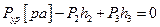 ,
,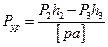
 Отрезки (плечи сил)
Отрезки (плечи сил) 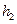 ,
, 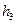 измеряются по чертежу (мм). Если на звенья действуют моменты, то их следует представить как пару сил, вычислив их величины и приложив в соответствующих точках. Например, если на звено 2 действует момент М2, то его представляем как пару сил
измеряются по чертежу (мм). Если на звенья действуют моменты, то их следует представить как пару сил, вычислив их величины и приложив в соответствующих точках. Например, если на звено 2 действует момент М2, то его представляем как пару сил 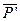 и
и 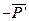 приложенных в точках А и В (рис, 1.3). Величины этих сил определяем по формуле
приложенных в точках А и В (рис, 1.3). Величины этих сил определяем по формуле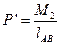


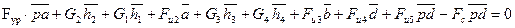
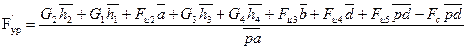
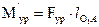
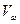 точки зацепления
точки зацепления 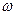 и в конце вектора скорости
и в конце вектора скорости 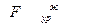 (рис. ). Тогда
(рис. ). Тогда