МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное
образовательное учреждение высшего образования
«Самарский национальный исследовательский университет
имени академика С.П. Королева»
(Самарский университет)
Кафедра основ конструирования машин
Лекции по курсу «Теория механизмов и машин»
Самара 2020
Оглавление
Лекция №1 - Основы строения механизмов и машин. Основные виды механизмов. 3
Лекция №2 - Образование механизмов. Структурный анализ механизма. 12
Лекция №3 - Кинематические характеристики механизмов. Графические и аналитические методы расчета кинематических характеристик. 18
Лекция №4 - Кинематический анализ зубчатых передач. 28
Лекция №5 - Проектирование зубчатых передач. Эвольвента, ее свойства и уравнения. 34
Лекция №6 - Качественные показатели зубчатой передачи. Особенности изготовление зубчатых колес. 44
Лекция №7 - Синтез и анализ кулачковых механизмов. 59
Лекция №8 - Силовой анализ механизмов. Характеристики сил, действующих на механизмы. Условия кинетостатической определимости. 74
Лекция №9 - Общая методика силового расчета. 80
Лекция №10 – продолжение силового расчета. 86
Лекция №10 - Исследование движения машин и механизмов. 92
Лекция №11 - Неравномерность движения машинного агрегата. Регулирование движения. 101
Лекция №1 - Основы строения механизмов и машин.
Основные виды механизмов
Находящиеся в настоящее время в эксплуатации механизмы и машины исключительно разнообразны по конструкции и назначению. В связи с этим подробное рассмотрение и детальное изучение отдельных механизмов и машин производится в курсах специальных дисциплин. Однако при изучении любого конкретного механизма или машины приходится рассматривать не только те вопросы, которые специфичны для данного механизма, но и ряд вопросов, относящихся в равной мере ко всем механизмам или к некоторой группе механизмов. Курс теории механизмов и машин предназначен для изучения тех вопросов исследования и проектирования механизмов и машин, которые являются общими для большинства механизмов и машин.
К таким вопросам относятся:
1) изучение траекторий, описываемых отдельными точками механизма;
2) определение скоростей и ускорений отдельных точек звеньев механизма;
3) определение угловых скоростей и ускорений отдельных звеньев механизма;
4) определение сил, действующих на звенья механизма;
5) изучение вредных сопротивлений;
6) определение механического КПД;
7) изучение характера движения механизма или машины в зависимости от приложенных сил;
8) изучение вопросов регулирования хода машины;
9) изучение уравновешенности механизмов и машин и ряд других вопросов.
Таким образом, можно сказать, что теория механизмов - есть наука, изучающая строение, кинематику и динамику механизмов и машин.
Структура и кинематика механизмов имеют своей целью: изучение теории механизмов, исследование движения звеньев механизмов с геометрической точки зрения независимо от сил, вызывающих движение этих элементов, а также изложение методов проектирования механизмов по заданным кинематическим условиям.
Динамика механизмов изучает методы определения сил, действующих на звенья механизмов и машин в процессе их движения, и исследует взаимосвязи между движением этих звеньев, силами, на них действующими и массами, которыми обладают эти элементы.
При этом изучаются такие важные вопросы, как определение сил инерции и их уравновешивание, силовой расчет механизмов, подбор двигателя к машине, обеспечение плавности хода машины ( в соответствии с требуемым режимом надежной ее работы), определение времени разгона и остановки машины. Динамика машин решает задачи регулирования хода машины и определения времени срабатывания. Первая задача имеет значение для поддержания необходимого режима работы двигателя в зависимости от производства.
Основателем русской школы теории механизмов и машин является великий русский математик и механик академик Пафнутий Львович Чебышев (1821-1894), ему принадлежит ряд оригинальных исследований, посвященных синтезу механизмов, теории регуляторов и зубчатых зацеплений, структуре плоских механизмов. В области теории механизмов и машин работали, такие выдающиеся ученые, как академик И.А.Вышнеградский (1831-1895), Н.Е.Жуковский (1847-1921), С.А.Чаплыгин (1869-1942) и др. Достижения отечественной школы теории механизмов и машин, в дореволюционный период заслуживают высокой оценки, однако подлинный расцвет она получила в СССР после Великой Октябрьской социалистической революции в связи с бурным развитием советского машиностроения. В кратком очерке невозможно перечислить многочисленные исследования советских ученых в этой области. Отметим, что плодотворно трудились в этой области такие крупные ученые как академик И.И.Артоболевский, чл.-кор. АН СССР, В.В.Добровольский (1880-1959), проф. докт. наук Г.Г.Баранов, Л.Н.Решетов, Кетов (1887-1948), Н.И. Колчин, Кожевников и др.
Одной из важнейших задач развития народного хозяйства нашей страны является комплексная механизация и автоматизация различных производственных процессов при значительном росте на этой основе производительности труда. Решение этой задачи требует от специалистов большой работы по созданию новых машин, механизмов, автоматических устройств по объединению станков в поточные автоматические линии и т.п.
Задача курса – дать основные сведения по проектированию механизмов и машин и осветить вопросы их механики, т.е. вопросы движения и работы.
В связи с этим любой инженер, в какой бы он области не работал, должен владеть основами знаний, которые позволяют решать поставленные задачи.
Структура и классификация механизмов.
Звенья, кинематические пары и кинематические цепи. (Классификация кинематических пар). Основные определения.
Всякий механизм состоит из отдельных деталей. Каждая подвижная деталь или несколько деталей, образующих одну жесткую подвижную систему тел, носит название подвижного звена механизма.
Неподвижным звеном или стойкой называются все неподвижные детали, образующие жесткую неподвижную систему тел.
Звенья, законы движения которых задаются, называются входными.
Звенья, законы движения которых определяются движением ведущих, называются ведомыми.
Совокупность двух звеньев, подвижно соединенных между собой, т.е. имеющих возможность относительного движения, называется кинематической парой.
Части звеньев, находящиеся в соприкосновении, называются элементами кинематической пары. Элементами кинематической пары могут быть: точка, линия или поверхность соприкосновения звеньев, образующих кинематическую пару.
В конструкциях механизмов машин и приборов встречается большое разнообразие кинематических пар. Классификация кинематических пар может быть двоякой:
а) классификация кинематических пар по числу условий связи;
б) классификация кинематических пар по характеру соприкосновения звеньев.
Ограничения, накладываемые на движение свободной точки, называются связями.
Любое перемещение свободного тела в пространстве можно рассматривать как совокупность 6 независимых друг от друга движений: 3-х поступательных движений параллельных осям координат x,y,z и 3-х вращательных движений относительно осей, параллельных осям x,y,z.
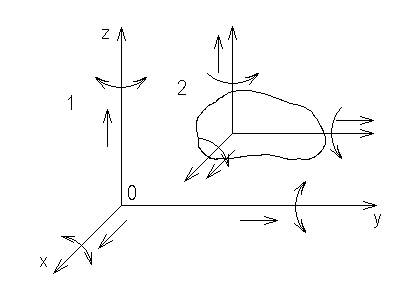
Принято считать в таком случае, что тело обладает 6-ю степенями свободы. Под степенями свободы понимают лишь те независимые одни от другого параметры, которые должны быть заданы для определения положения тела или точки.
Допустим звенья 1 и 2 подвижно соединены друг с другом, т.е. образуют в совокупности кинематическую пару. В этом случае уже нельзя считать звенья 1 и 2 свободными телами. В зависимости от вида соединения звеньев звено 1 сможет совершать 1, 2, 3, 4 или 5 движений относительно звена 2. Т.е. на относительное движение звеньев будет наложено соответствующее количество условий связи. Все кинематические пары в зависимости от числа условий связей, налагаемых ими на относительное движение звеньев, делятся на классы (5 классов).
а) Класс кинематической пары определяется числом условий связи, накладываемых на относительное движение ее звеньев.
Номер класса пары совпадает с числом условий связи, накладываемых парой на относительное движение звеньев. Если число связей =1, то кинематическая пара относится к 1-му классу, если число связей =2, то ко 2-му классу и т.д.
Примеры кинематических пар различных классов.
I S=1
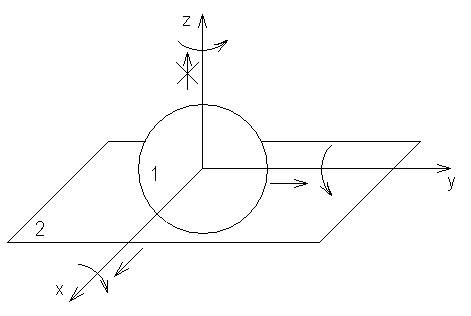
Шар на плоскости. Кинематическая пара I класса, т.к. число связей, накладываемых на относительное движение звеньев =1.
II S=2
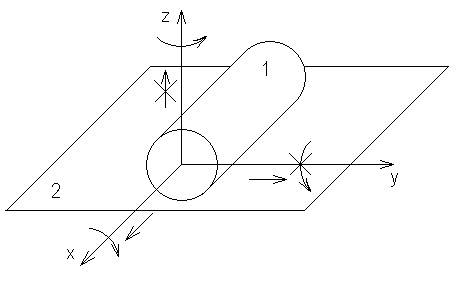
Цилиндр на плоскости. Кинематическая пара II класса. Наложено 2 условия связи: исключено поступательное движение вдоль оси z и вращательное вокруг оси y.
III S=3
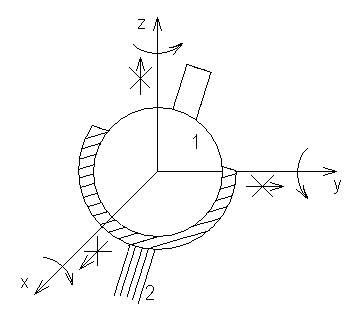
Шаровой шарнир. Кинематическая пара III класса. Движение звена 1 относительно 2 сводится только к вращению вокруг осей x, y, z.
IV S=4
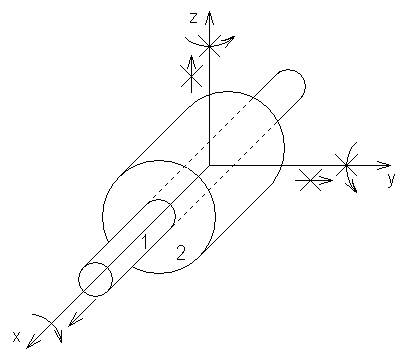
Цилиндр во втулке. Относится к кинематической паре IV класса.
V S=5
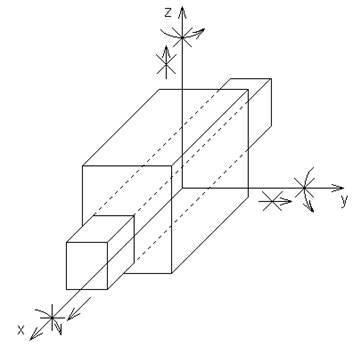
Призматическая поступательная пара V класса. Винтовая пара.
При определении класса кинематической пары учитывать только независимые возможные движения.
б) Классификация кинематических пар по характеру соприкосновения звеньев.
Кинематические пары разделяются на низшие и высшие.
Низшими кинематическими парами называются такие пары, в которых соприкосновение элементов кинематической пары происходит по поверхности.
Высшими кинематическими парами называются такие пары, в которых соприкосновение элементов происходит в точке или по линии (например, кинематическая пара, образуемая соприкасающимися зубьями зубчатых колес).
Низшие кинематические пары встречаются в следующих разновидностях: вращательная, поступательная, шаровая и винтовая. Большим преимуществом низших кинематических пар по сравнению с высшими кинематическими парами является:
1) способность их элементов воспринимать и передавать значительные силы при меньшем износе;
2) технологически легче изготовить низшие кинематические пары;
3) с точки зрения динамики механизмы с низшими кинематическими парами работают надежнее, чем с высшими кинематическими парами. Низшие кинематические пары обратимы, а высшие - нет;
4) механизмы, имеющие в своем составе высшие кинематические пары и низшие кинематические пары, точно воспроизводят заданный закон движения, чего часто нельзя добиться при помощи механизмов, имеющих только низшие кинематические пары.
Достоинством высших кинематических пар является возможность воспроизводить достаточно сложные относительные движения.
Кинематической цепью называется последовательное соединение звеньев, входящих в кинематическую пару. Кинематические цепи могут быть открытыми и замкнутыми, плоскими и пространственными.
В открытой цепи имеются звенья, входящие в состав только одной кинематической пары, т.е. соединяющиеся только с одним звеном, например звено 1 и 4.
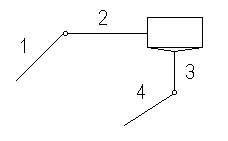
Замкнутой называется цепь, в которой каждое звено входит по крайней мере в состав 2-х кинематических пар.
В конструкциях механизмов можно встретить как открытые, так и замкнутые кинематические цепи. Примером открытой кинематической цепи являются обычные рычажные весы. В машиностроении преимущественно применяются замкнутые кинематические цепи. В машинах и приборах наиболее широкое применение получили плоские кинематические цепи. К плоским цепям относятся цепи, все точки звеньев которых совершают плоскопараллельное движение (движение в одной или параллельных плоскостях). Точки звеньев пространственных цепей описывают либо пространственные кривые, либо плоские кривые, расположенные в непересекающихся плоскостях.
Из всего вышесказанного можно дать следующее определение механизма.
Механизм называется кинематическая цепь, имеющая вполне определенное движение всех ведомых звеньев при неподвижной стойке (станине) и при заданном движении одного или нескольких ведущих звеньев.
Числом ведущих звеньев определяется (для плоских механизмов) степень подвижности механизма или, что, то же самое, число его степеней свободы относительно стойки. Иначе, число степеней свободы механизма показывает, сколько надо задать независимых координат, чтобы характеризовать положение ведущего звена механизма по отношению стойки (неподвижная система координат).
Машиной называется механизм или комплекс механизмов, предназначенных для выполнения полезной работы, связанной с процессом производства или преобразования энергии.
В машиностроении наибольшее значение имеют плоские механизмы, поэтому мы уделим им наибольшее внимание.
Степень подвижности плоских механизмов.
Выведем формулу для определения (подвижности) числа степеней подвижности плоского механизма, т.е. такого механизма, звенья которого совершают плоскопараллельное движение. В этом случае из 6 простейших движений, которые каждое отдельное звено может совершать в пространстве, исключаются 3 движения – одно поступательное и 2 вращательных. Следовательно, принимая во внимание эти исключенные движения, можно условно считать, что число простейших движений каждого свободного звена равно в этом случае 3. При этом условии в состав плоских кинематических цепей могут входить лишь кинематические пары 5 и 4 класса. Пары 1, 2 и 3 класса входить в плоские механизмы не могут, т.к. эти пары допускают 3 и более возможных относительных движений входящих в них звеньев. Пара 5-го класса будет лишать каждое образующее ее звено 2-х из 3-х оставшихся простейших движений, а пара 4-го класса – одного простейшего движения.
Пусть плоский механизм состоит из “k” звеньев при одном неподвижном, из которых образованы кинематические пары 5-го класса в количестве 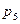 и 4-го класса в количестве
и 4-го класса в количестве 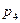 . Все
. Все 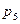 кинематические пары 5-го класса лишат подвижные звенья
кинематические пары 5-го класса лишат подвижные звенья  простейших движений, а все
простейших движений, а все 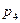 кинематические пары 4-го класса -
кинематические пары 4-го класса - 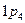 простейших движений. В результате число степеней свободы плоского механизма
простейших движений. В результате число степеней свободы плоского механизма 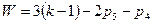 или
или 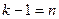 ,
, 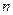 - число подвижных звеньев, тогда
- число подвижных звеньев, тогда 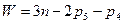 . Эта формула впервые была выведена академиком Чебышевым в 1869г и теперь называется формулой Чебышева. Формула Чебышева называется структурной формулой плоских механизмов, поскольку она устанавливает зависимость числа степеней подвижности от ее структуры. Число ведущих звеньев в механизме и число степеней свободы должны совпадать, только в этом случае мы получим определенное и однозначное перемещение звеньев.
. Эта формула впервые была выведена академиком Чебышевым в 1869г и теперь называется формулой Чебышева. Формула Чебышева называется структурной формулой плоских механизмов, поскольку она устанавливает зависимость числа степеней подвижности от ее структуры. Число ведущих звеньев в механизме и число степеней свободы должны совпадать, только в этом случае мы получим определенное и однозначное перемещение звеньев.
Кинематические пары 5-го класса, входящие в состав плоского механизма, могут существовать в 2-х видах: либо в виде вращательной пары, либо в виде поступательной пары.
Рассмотрим пример: Кривошипно-ползунный механизм имеет весьма широкое применение. В частности, он служит основным механизмом двигателя внутреннего сгорания.
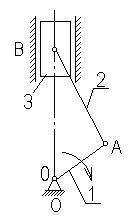
Механизм имеет 3 подвижных звена: 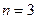 , стойка 0. Звенья 1 и 0 образуют пару 5-го класса (вращ.). Вращательные пары образованы также звеньями 1 и 2 (кривошип и шатун) и звеньями 2 и 3 (шатун и ползун). Звенья 3 и 0 образуют пару 5-го класса поступательную. Пар 4-го класса механизм не содержит. Таким образом, у рассматриваемого механизма
, стойка 0. Звенья 1 и 0 образуют пару 5-го класса (вращ.). Вращательные пары образованы также звеньями 1 и 2 (кривошип и шатун) и звеньями 2 и 3 (шатун и ползун). Звенья 3 и 0 образуют пару 5-го класса поступательную. Пар 4-го класса механизм не содержит. Таким образом, у рассматриваемого механизма
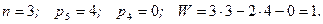
Как видим, рассматриваемый механизм обладает одной степенью свободы. Это означает, что если одному из звеньев механизма сообщить определенное движение, то все его остальные подвижные звенья также получат вполне определенные движения, являющиеся функциями заданного. Сообщив, например, кривошипу 1 вращение с определенной угловой скоростью, мы заставим ползун 3 перемещаться поступательно, причем скорость V поступательного перемещения ползуна в каждое мгновение времени будет также вполне определенной.
Таким образом, число степеней свободы механизма W показывает, сколько независимых простейших движений должно быть сообщено одному или нескольким звеньям механизма, чтобы все его звенья двигались вполне определенно.
Степень подвижности механизма.
Примем следующие обозначения:
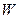 - степень подвижности механизма;
- степень подвижности механизма;
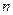 - число подвижных звеньев;
- число подвижных звеньев;
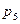 - число пар 5-го класса (пост. и вращ.);
- число пар 5-го класса (пост. и вращ.);
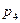 - число пар 4-го класса (высшие пары, касание зубьев, касание ролика с кулачком)
- число пар 4-го класса (высшие пары, касание зубьев, касание ролика с кулачком)
Свободное звено на плоскости обладает 3-мя степенями свободы; “ 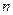 ” свободных звеньев имеют “
” свободных звеньев имеют “ 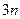 ” степеней свободы. Если из этих “
” степеней свободы. Если из этих “ 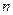 ” звеньев образован механизм, в котором количество кинематических пар 5-го класса будет -
” звеньев образован механизм, в котором количество кинематических пар 5-го класса будет - 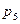 , кинематических пар 4-го класса -
, кинематических пар 4-го класса - 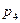 , то число условий связи, накладываемых парами 5-го класса, будет
, то число условий связи, накладываемых парами 5-го класса, будет  , а парами 4-го класса -
, а парами 4-го класса - 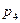 , т.к. каждая пара 5-го класса при плоском движении накладывает 2 условия связи, а пара 4-го класса – 1 условие связи, тогда
, т.к. каждая пара 5-го класса при плоском движении накладывает 2 условия связи, а пара 4-го класса – 1 условие связи, тогда 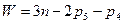 .
.
В состав плоского механизма могут входить только пары 5-го и 4-го класса, причем низшие пары могут быть только 2-х типов: поступательные и вращательные. Конструктивных форм высших пар в технике очень много.
Необходимо отметить, что кроме степеней свободы звеньев и связей, воздействующих на характер движения механизмов, в них могут встретиться степени свободы и условия связи, не оказывающие влияния на характер движения механизма в целом, такие степени свободы называются лишними, а связи называются пассивными связями.
Особые случаи структурного анализа.
Механизмы с лишними степенями свободы.
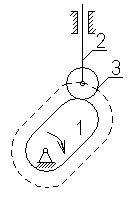
Подсчитаем степень подвижности кулачкового механизма: 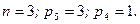
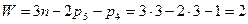 .
.
Этот результат получается, потому что ролик круглый и центр вращательной пары совпадает с геометрическим центром.
Формально в данном механизме надо назначить 2 ведущих звена 1и 3. Но вследствие того, что рабочая часть звена 3 имеет круглую форму, его движение не влияет на кинематику остальных звеньев механизма. Такие механизмы называются механизмами с лишними степенями свободы.
Лишними степенями свободы называются подвижности звеньев, не влияющие на степень свободы механизма в целом.
Лишняя степень свободы применяется в механизмах для увеличения КПД и уменьшения износа.
Можно, не нарушая характера движения всех других звеньев механизма, удалить ролик 3, а профиль кулачка эквидистантно увеличить на радиус ролика.
Тогда будем иметь 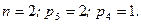
Если ролик сделать некруглым или при круглом ролике центр вращения расположить вне геометрического центра, то для определенного движения необходимо 2 ведущих звена.
Механизмы могут содержать так называемые пассивные связи, не влияющие на механизм в целом.
Механизмы с пассивными связями.
Подсчитаем степень подвижности механизма параллелограмма тепловоза. В технике этот механизм применяется для передачи равномерного движения от звена 1 к звену 3.
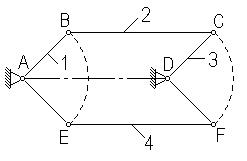
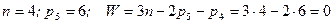 , т.е. при подсчете по структурному уравнению получается, что данная схема представляет собой ферму. В действительности же, в силу особых метрических соотношений между звеньями AB=CD, AE=DF, BC=AD=EF – расстояние между E и F не изменяется. Это механизм с одной степенью свободы. Если из схемы удалить звено EF, то кинематика остальных звеньев не изменится. Тогда будет:
, т.е. при подсчете по структурному уравнению получается, что данная схема представляет собой ферму. В действительности же, в силу особых метрических соотношений между звеньями AB=CD, AE=DF, BC=AD=EF – расстояние между E и F не изменяется. Это механизм с одной степенью свободы. Если из схемы удалить звено EF, то кинематика остальных звеньев не изменится. Тогда будет: 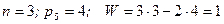 , т.е. данная схема представляет механизм с одной степенью свободы.
, т.е. данная схема представляет механизм с одной степенью свободы.
Пассивными связями называются связи, не влияющие на кинематику механизма, но вызывающие статическую неопределенность.
Заранее учесть в механизме наличие пассивных связей трудно. Их можно обнаружить при более детальном обследовании механизма. Однако, можно сказать, что пассивные связи появляются в случае параллельных или совпадающих траекторий.
При определении степени (свободы) подвижности механизма пассивные связи и лишние степени свободы не учитываются.
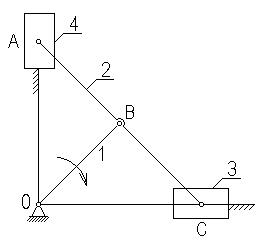
Пассивные связи применяются в механизмах для увеличения жесткости механизма или распределения нагрузки и для прохождения звеньев через мертвые положения.
На схеме эллипсографа 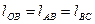 и один из ползунов является пассивной связью.
и один из ползунов является пассивной связью.
Лекция №2 - Образование механизмов. Структурный анализ механизма
В современном машиностроении все многообразие механизмов разбито на различные классы и группы в зависимости от общих классификационных признаков.
Структурный анализ механизма всегда предшествует его кинематическому и силовому расчетам.
Механизмы одного и того же класса имеют общие методы расчетов.
Деление механизмов на классы производится по структурным особенностям групп, составляющих данные механизм.
Структурные группы. Класс, порядок, вид групп Ассура. Согласно Л.В.Ассуру любой механизм образуется последовательным присоединением к входному звену (со стойкой) кинематических цепей, степень подвижности которых равна нулю. Такие цепи называются структурными группами Ассура. Если степень подвижности W=0, то число звеньев и пар плоского механизма, входящих в группу, связаны соотношением
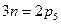
Это уравнение имеет множество решений, состоящих из четного числа звеньев и кинематических пар 5-го класса, количество которых кратно 3.
Группами Ассура будут являться только неделимые цепи, т.е. такие, которые без разрушения нельзя разделить на самостоятельные структурные группы.
Класс, порядок, вид структурных групп. Группы Ассура разделяются на классы, каждая структурная группа имеет порядок, а в одном из классов, втором, различают еще и виды групп.
Класс группы Ассура определяется наивысшим классом контура, входящего в ее состав (табл. 1)
Таблица1 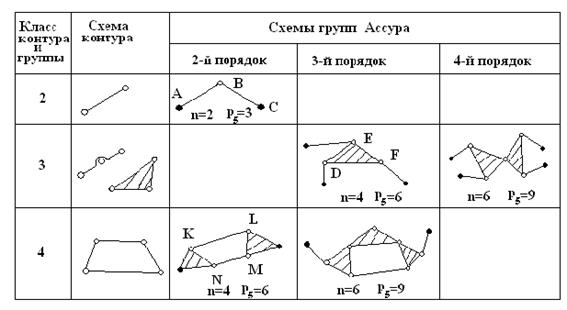
Кинематическая цепь, состоящая из двух звеньев и трех кинематических пар (n=2; 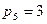 ), всегда является группой Ассура второго класса.
), всегда является группой Ассура второго класса.
Порядок структурной группы определяется числом внешних, свободных кинематических пар, которыми она присоединяется к другим звеньям механизма. В табл. 1 внешние пары затушеваны, они и определяют порядок структурной группы. Кинематические пары, входящие в замкнутый контур, называются внутренними. У групп Ассура второго класса всегда 2-й порядок.
Группы Ассура 2-го класса разделяются на пять видов, зависящих от взаимного расположения в группе вращательных и поступательных кинематических пар.
Виды групп Ассура 2-го класса представлены на рис. 1.
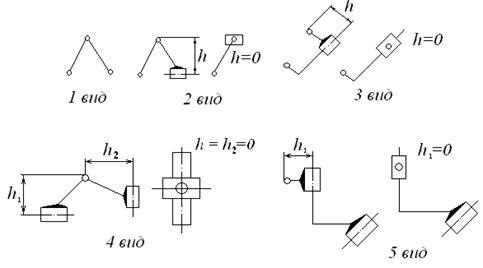
Рис. 1. Виды групп Ассура 2-го класса
Класс группы Ассура выше второго определяется числом внутренних кинематических пар, образующих замкнутый контур (табл. 1, контуры 3 и 4). Ведущее звено вместе со стойкой и кинематической парой, соединяющей их, называется механизмом 1-го класса и указывается стрелкой, направленной по движению ведущего звена.
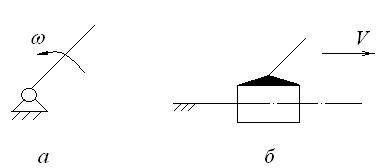
Рис.2. Вращающееся ведущее (а) и поступательно движущееся (б) звенья
На рис. 2а представлено вращающееся ведущее звено, а на рис.2б
поступательно движущееся. Конструктивные особенности звеньев, не оказывающие влияния на движение механизма, на схемах не учитываются.
Класс механизма определяется наивысшим классом структурной группы, входящей в этот механизм. При определении класса механизма необходимо указать, какие звенья являются ведущими, т. к. в зависимости от выбора ведущих звеньев класс механизма может измениться.
В структурные группы входят только цепи с низшими кинематическими парами. Если в механизме имеются цепи с высшими кинематическими парами, каждая высшая пара должна быть заменена, и только после этого заменяющий механизм разбивается на структурные группы Ассура.
2. Замена высшей пары в плоском механизме
Каждая высшая кинематическая пара эквивалентна одному звену, оканчивающемуся двумя низшими парами. Вид низших пар зависит от соприкасающихся поверхностей звеньев.
Правила замены. Необходимо найти радиусы кривизны соприкасающихся поверхностей, в центре кругов кривизны поставить условные шарниры и между ними добавочное звено (рис. За). Если одна из контактируемых поверхностей прямолинейна, движение будет поступательным, а заменяющая пара -ползуном (рис. 3б).
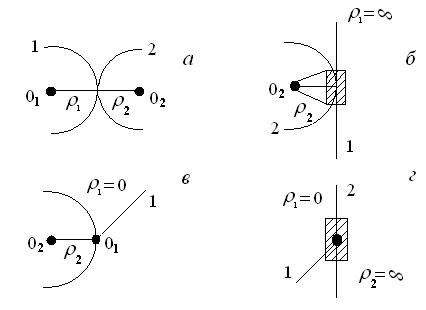
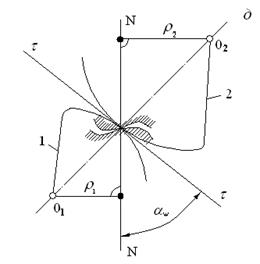
Рис.3. Замена высших пар низшими
3.Структурный анализ механизма
Структурным анализом механизма называют определение количества ведущих звеньев, групп Ассура, последовательность их присоединения к кинематической цепи и класс механизма.
Структурный анализ возможен, если соблюдаются следующие условия:
I)число ведущих звеньев равно числу степеней свободы механизма;
2) ведущее звено входит в кинематическую пару со стойкой;
3)все кинематические пары относятся к 5-му классу.
Структура любого плоского механизма наглядно представляется с помощью формулы его строения. Формула строения механизма состоит из условного обозначения класса, порядка и вида каждой структурной группы, и схематично показывает порядок присоединения структурных групп к ведущим звеньям.
Например, если формула строения механизма
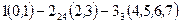
то первая цифра 1 указывает на механизм 1-го класса, в скобках (0-стойка, 1 -ведущее звено), т. е. ведущее звено со стойкой. Затем к ведущему звену присоединяется группа 2-го класса, 2-го порядка, 4-го вида; в скобках указаны номера звеньев, ее образующие.
В группе Ассура 3-го класса, 3-го порядка в скобках указаны номера звеньев, ее образующие. Одно из них поставлено в числителе, и оно носит название базисного, потому что к нему присоединяются более чем два других звена (их номера перечислены в знаменателе: 5, 6, 7).
Класс данного механизма третий, т. к. наивысший класс группы, входящей в этот механизм, - три.
4. Порядок проведения структурного анализа
1. Подсчитывается степень подвижности механизма по формуле Чебышева, для чего нумеруются подвижные звенья и определяется количество кинематических пар. При наличии высших кинематических пар их надо заменить цепями с низшими кинематическими парами.
Если в механизме есть лишние степени подвижности, их не учитывают. Могут оказаться в механизме и пассивные связи, которые не оказывают влияния на работу механизма. Применяются они в механизмах для увеличения жесткости, для более правильного распределения нагрузок. Лишние степени свободы служат для увеличения к.п.д. механизма и уменьшения износа.
Производится отделение групп Ассура, начиная с наиболее удаленной от ведущего звена. Если возможно, отделяется группа наиболее низкого класса. Если такую группу выделить невозможно, отделяется группа более высокого класса. Разложение механизма на структурные группы ведется до тех пор, пока не останутся ведущее звено и стойка. При этом необходимо проверять замкнутость оставшейся кинематической цепи. Каждое звено и любая кинематическая пара должны входить только в одну из структурных групп.
Записывается формула строения механизма, начиная с ведущего звена (механизма 1-го класса) и далее в порядке присоединения групп Ассура.
Указывается класс механизма.
5.Примеры структурного анализа
Пример 1. Кулачково-коромысловый механизм
Ролик 3 кулачкового механизма (рис. 4 а), образуя с коромыслом 2 вращательную пару 5-го класса, создает в механизме лишнюю степень подвижности. Он свободно вращается на своей оси, не оказывая никакого влияния на характер движения механизма. Ролик поставлен из конструктивных соображений для замены трения скольжения трением качения. Поэтому ролик 3 можно условно жестко закрепить коромыслом со звеном 2 (рис. 4 б). Тогда число подвижных звеньев механизма n=2, количество вращательных пар 5-го класса 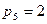 , они находятся в точках
, они находятся в точках 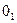 и
и 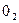 , в точке контакта коромысла с кулачком - высшая пара 4-го класса,
, в точке контакта коромысла с кулачком - высшая пара 4-го класса, 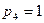 .
.
Степень подвижности механизма
W=3*2*2*2 -1 = 1.
Ведущим звеном выбран кулачок 1.
Высшая пара должна быть заменена добавочным условным звеном k (длина которого равна сумме радиусов кривизны 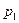 и
и 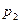 соприкасающихся поверхностей 1 и 2) и двумя низшими парами А и В, расположенными в центрах кривизны (рис. 4в).
соприкасающихся поверхностей 1 и 2) и двумя низшими парами А и В, расположенными в центрах кривизны (рис. 4в).
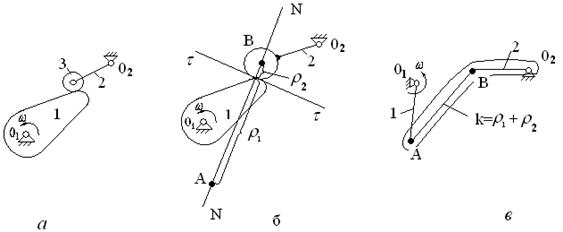
Рис.4 Пример структурного анализа механизма с лишней степенью подвижности и высшей кинематической парой
Мгновенно заменяющий механизм представлен на рис.4в.
Кинематическая цепь этого механизма состоит из структурной группы 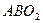 2-го класса,2-го порядка и 1-го вида и ведущего звена
2-го класса,2-го порядка и 1-го вида и ведущего звена 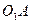 . Формула его строения:
. Формула его строения:
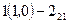 .
.
Заменяющий механизм относится к механизму 2-го класса.
Исходный кулачковый механизм также относится к механизму 2-го класса.
Пример 2. Механизм с изменяемым классом
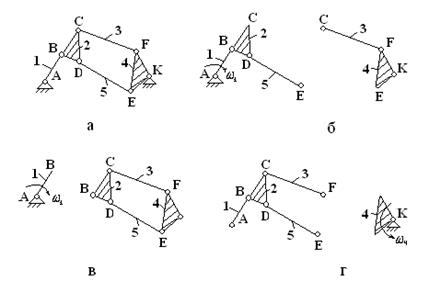
Рис.5.Пример структурного анализа механизма с изменяемым классом
Степень подвижности исходного механизма при n=5 и 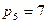 (рис.5а) W=3*5-2*7=1 указывает на наличие в нем одного ведущего звена.
(рис.5а) W=3*5-2*7=1 указывает на наличие в нем одного ведущего звена.
Допустим, что входным звеном выбрано звено 1 (рис.5б). Делается попытка отделить от механизма группу Ассура 2-го класса ((n =2, 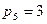 ); звенья 3 и 4). Тогда оставшаяся цепь звеньев 1, 2, 5 будет незамкнутой, что приводит к неопределенности движения звеньев 2 и 5. Тот же результат получается при отделении от механизма звеньев 4, 5.
); звенья 3 и 4). Тогда оставшаяся цепь звеньев 1, 2, 5 будет незамкнутой, что приводит к неопределенности движения звеньев 2 и 5. Тот же результат получается при отделении от механизма звеньев 4, 5.
Правильное решение дает выделение из механизма группы Ассура, состоящей из четырех звеньев 2, 3, 4, 5 и шести пар (рис. 5в). Это группа Ассура .4. После отделения остается входное звено 1 и стойка 0 (механизм 1-го класса). Формула строения механизма в данном случае:
1(0,4)- 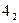 (2,3,4,5),
(2,3,4,5),
т.е. механизм 4-го класса.
Если в данном механизме выбрать за входное звено 4, то класс его изменяется (рис. 5г). Цепь его ведомых звеньев 1, 2, 3, 5 представляет собой трехповодковую группу Ассура 3-го класса 3-го порядка. Формула строения механизма в этом случае:
1(0,4)- 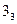 (2,1,3,5),
(2,1,3,5),
т.е механизм 3-го класса.
Таким образом, замена ведущего (начального) звена привела к понижению класса механизма.
Лекция №3 - Кинематические характеристики механизмов. Графические и аналитические методы расчета кинематических характеристик.
При кинематическом анализе механизмов решают две основные задачи:
Определение положений звеньев и траекторий точек;
Определение линейных и угловых скоростей и ускорений.
Из анализа положений звеньев и траекторий их точек можно определить правильность действия механизма и соответствие траекторий точек рабочего органа технологическому процессу, а также найти пространство, требуемое для размещения механизма.
Скорости (линейные и угловые) используют для определения кинетической энергии механизма при решении в последующем задач динамики и для оценки условий, при которых происходит рабочий процесс в машине.
По значениям ускорений (линейных и угловых) находят инерционные нагрузки на звенья.
Кинематические характеристики необходимы инженеру для оценки работоспособности механизмов не только на стадии проектирования, но и в эксплуатации.
Для определения кинематических параметров механизма используют аналитические, графические и экспериментальные методы.
Кинетический анализ проводят при обязательном задании кинематической схемы механизма, которая в отличие от структурной схемы содержит размеры звеньев и задании закона движения входного звена.
Кинематическая схема вычерчивается с учетом масштабного коэффициента.
Масштабным коэффициентом называется отношение какой-либо линейной или физической величины к отрезку, его изображающему на чертеже:
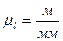
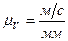
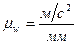
где: 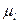 масштабный коэффициент длины звеньев;
масштабный коэффициент длины звеньев;
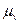 масштабный коэффициент линейных скоростей точек;
масштабный коэффициент линейных скоростей точек;
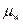 масштабный коэффициент линейных ускорений точек.
масштабный коэффициент линейных ускорений точек.
Пример составления кинематической схемы механизма дан на рис.1
Истинная длина звена – м
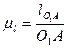 = Чертежная длина звена мм
= Чертежная длина звена мм
Задав чертежную длину звена 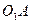 , разбивают цикл вращения входного звена
, разбивают цикл вращения входного звена 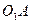 на равные части (через
на равные части (через 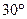 ) и, согласно его положениям, с помощью засечек строят положения остальных звеньев, предварительно определив чертежные длины этих звеньев
) и, согласно его положениям, с помощью засечек строят положения остальных звеньев, предварительно определив чертежные длины этих звеньев
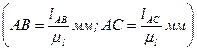 и т.д.
и т.д.
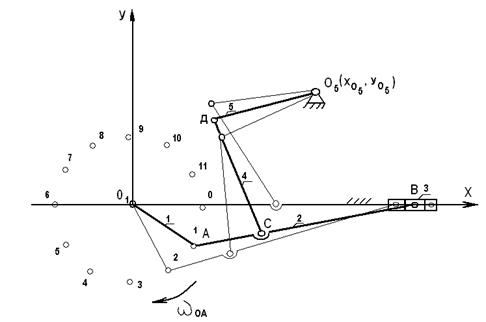
Рис.1
1.Построение плана скоростей и ускорений.
Планом скоростей (или ускорений) механизма называют чертеж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению скоростям (или ускорениям) различных точек звеньев механизма в данный момент. Все абсолютные скорости (или ускорения) выходят из одной точки, называемой полюсом плана скоростей (или ускорений).
В качестве примера построения планов скоростей и ускорений предлагается механизм, кинематическая схема которого приведена на рис.2.
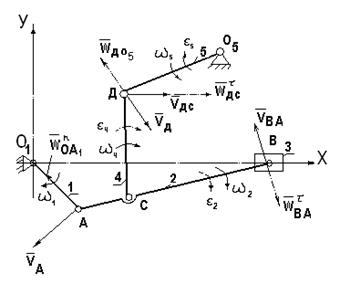
Рис.2 План скоростей.
Построение плана ведут в следующей последовательности:
1.входное звено  вращается с заданной угловой скоростью
вращается с заданной угловой скоростью 












 и 4-го класса в количестве
и 4-го класса в количестве  . Все
. Все  простейших движений, а все
простейших движений, а все 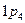 простейших движений. В результате число степеней свободы плоского механизма
простейших движений. В результате число степеней свободы плоского механизма 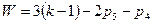 или
или 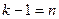 ,
, 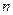 - число подвижных звеньев, тогда
- число подвижных звеньев, тогда 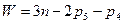 . Эта формула впервые была выведена академиком Чебышевым в 1869г и теперь называется формулой Чебышева. Формула Чебышева называется структурной формулой плоских механизмов, поскольку она устанавливает зависимость числа степеней подвижности от ее структуры. Число ведущих звеньев в механизме и число степеней свободы должны совпадать, только в этом случае мы получим определенное и однозначное перемещение звеньев.
. Эта формула впервые была выведена академиком Чебышевым в 1869г и теперь называется формулой Чебышева. Формула Чебышева называется структурной формулой плоских механизмов, поскольку она устанавливает зависимость числа степеней подвижности от ее структуры. Число ведущих звеньев в механизме и число степеней свободы должны совпадать, только в этом случае мы получим определенное и однозначное перемещение звеньев.
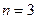 , стойка 0. Звенья 1 и 0 образуют пару 5-го класса (вращ.). Вращательные пары образованы также звеньями 1 и 2 (кривошип и шатун) и звеньями 2 и 3 (шатун и ползун). Звенья 3 и 0 образуют пару 5-го класса поступательную. Пар 4-го класса механизм не содержит. Таким образом, у рассматриваемого механизма
, стойка 0. Звенья 1 и 0 образуют пару 5-го класса (вращ.). Вращательные пары образованы также звеньями 1 и 2 (кривошип и шатун) и звеньями 2 и 3 (шатун и ползун). Звенья 3 и 0 образуют пару 5-го класса поступательную. Пар 4-го класса механизм не содержит. Таким образом, у рассматриваемого механизма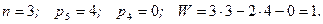
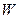 - степень подвижности механизма;
- степень подвижности механизма;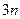 ” степеней свободы. Если из этих “
” степеней свободы. Если из этих “ 
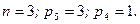
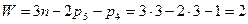 .
.
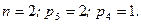
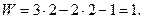

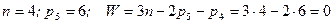 , т.е. при подсчете по структурному уравнению получается, что данная схема представляет собой ферму. В действительности же, в силу особых метрических соотношений между звеньями AB=CD, AE=DF, BC=AD=EF – расстояние между E и F не изменяется. Это механизм с одной степенью свободы. Если из схемы удалить звено EF, то кинематика остальных звеньев не изменится. Тогда будет:
, т.е. при подсчете по структурному уравнению получается, что данная схема представляет собой ферму. В действительности же, в силу особых метрических соотношений между звеньями AB=CD, AE=DF, BC=AD=EF – расстояние между E и F не изменяется. Это механизм с одной степенью свободы. Если из схемы удалить звено EF, то кинематика остальных звеньев не изменится. Тогда будет: 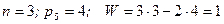 , т.е. данная схема представляет механизм с одной степенью свободы.
, т.е. данная схема представляет механизм с одной степенью свободы.
 и один из ползунов является пассивной связью.
и один из ползунов является пассивной связью.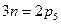

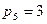 ), всегда является группой Ассура второго класса.
), всегда является группой Ассура второго класса.



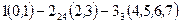
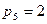 , они находятся в точках
, они находятся в точках 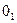 и
и 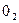 , в точке контакта коромысла с кулачком - высшая пара 4-го класса,
, в точке контакта коромысла с кулачком - высшая пара 4-го класса, 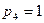 .
.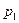 и
и 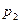 соприкасающихся поверхностей 1 и 2) и двумя низшими парами А и В, расположенными в центрах кривизны (рис. 4в).
соприкасающихся поверхностей 1 и 2) и двумя низшими парами А и В, расположенными в центрах кривизны (рис. 4в).
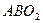 2-го класса,2-го порядка и 1-го вида и ведущего звена
2-го класса,2-го порядка и 1-го вида и ведущего звена 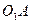 . Формула его строения:
. Формула его строения: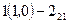 .
.
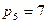 (рис.5а) W=3*5-2*7=1 указывает на наличие в нем одного ведущего звена.
(рис.5а) W=3*5-2*7=1 указывает на наличие в нем одного ведущего звена.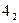 (2,3,4,5),
(2,3,4,5),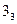 (2,1,3,5),
(2,1,3,5),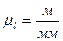
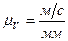
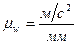
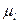 масштабный коэффициент длины звеньев;
масштабный коэффициент длины звеньев;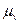 масштабный коэффициент линейных скоростей точек;
масштабный коэффициент линейных скоростей точек;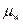 масштабный коэффициент линейных ускорений точек.
масштабный коэффициент линейных ускорений точек.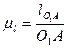 = Чертежная длина звена мм
= Чертежная длина звена мм ) и, согласно его положениям, с помощью засечек строят положения остальных звеньев, предварительно определив чертежные длины этих звеньев
) и, согласно его положениям, с помощью засечек строят положения остальных звеньев, предварительно определив чертежные длины этих звеньев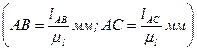 и т.д.
и т.д.




