Жидкость со средней вязкостью с условием

5. Жидкость с Вязкостью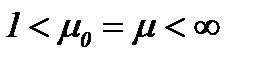  

Рассмотрим вязкую жидкость с небольшим числом Рейнольдса, где все инерционные члены содержатся в уравнениях Навье-Стокса для несжимаемой жидкости с вязкостью [12]. Выше отмечено, что уравнения Навье-Стокса такого вида, если не считать работы [8, 9], не исследованы в полном объеме. Технические приложения теории жидкости ограничены при очень больших значениях вязкости, если не поднимать вопросы теории смазки и падение маленьких шариков в густом масле [12]. Однако теоретические исследования в этом направлении важны для науки и практики. Это вызывает к разработке методов интегрирования уравнений Навье-Стокса со средним размером вязкости при наличии всех членов уравнения, поэтому в данном параграфе разработаны методы решения таких задач в пространстве 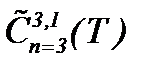 и класс подходящих решений, построенных на основе леммы K. Фридрихса [15] в .    

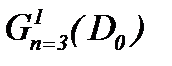Для этого модифицируются основные методы параграфа 4: (4.2) и (4.12) на основе регулирующих функций 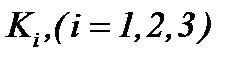, причем задача (1.1) – (1.3) не допускает ограничений (А₁) и (А₂), в чем и заключается актуальность исследований этого параграфа.

 5.1. Жидкость со средней вязкостью с условием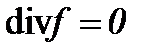

 Итак, если исходные данные 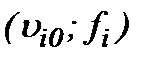 подчинены условию

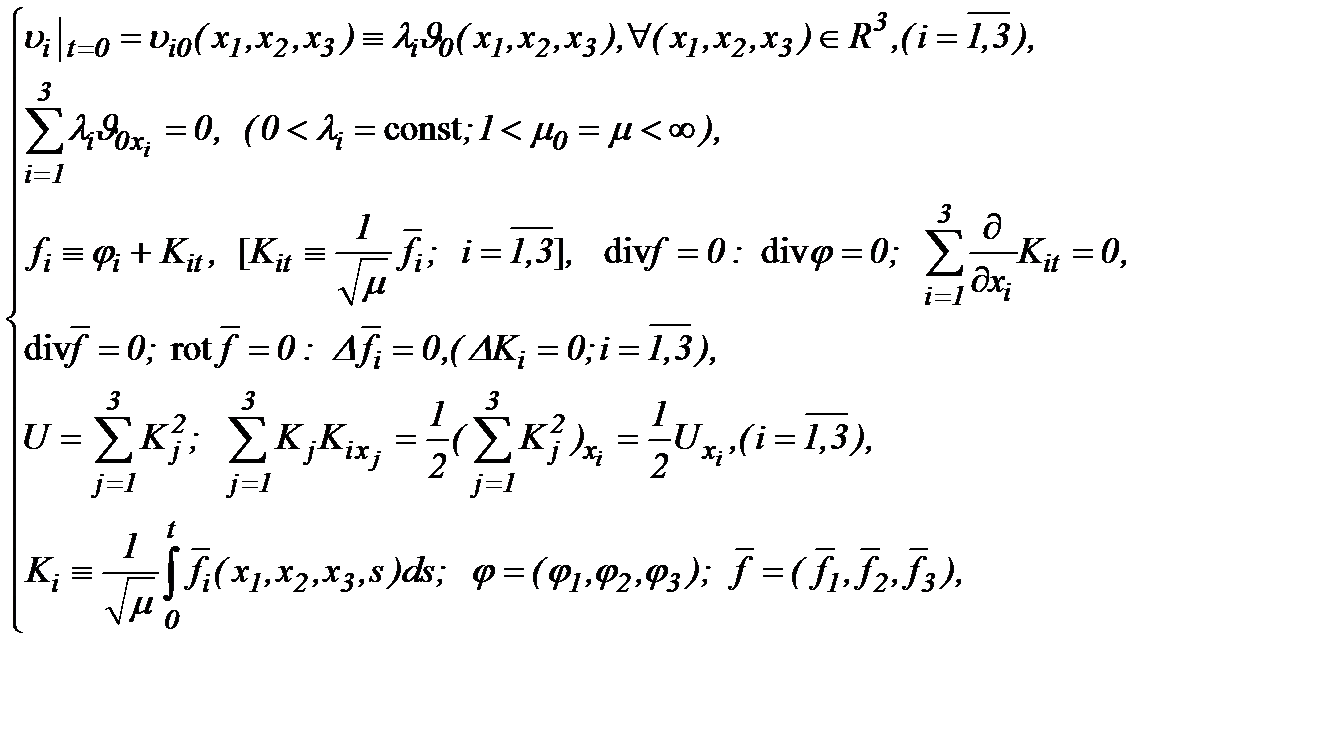                   (5.1)

 

 

то для определения компонент скоростей введем следующее правило   

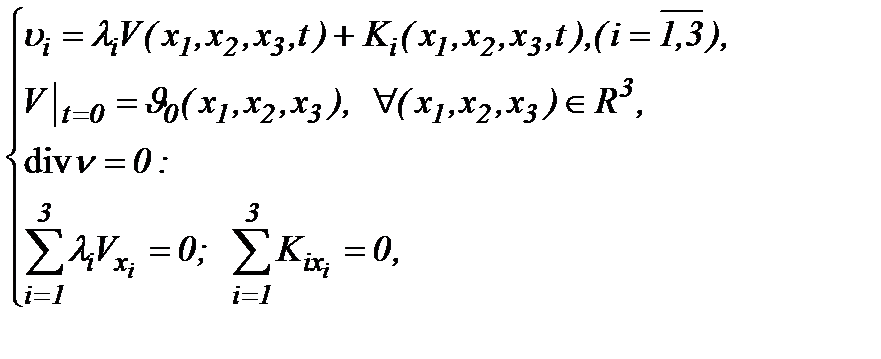                                            (5.2)

причем

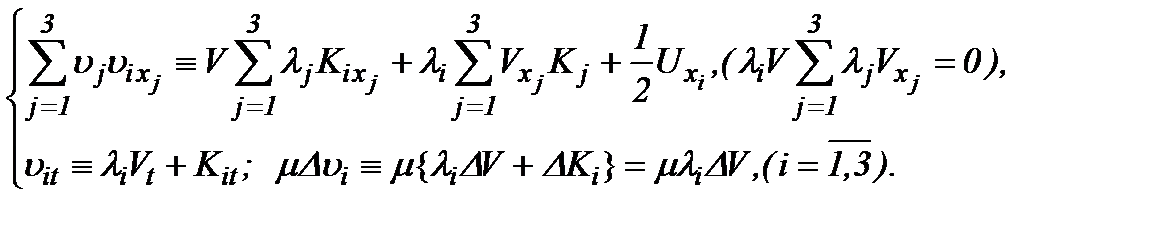                        (5.3)

 

Тогда, принимая во внимание (5.2) и (5.3), получим

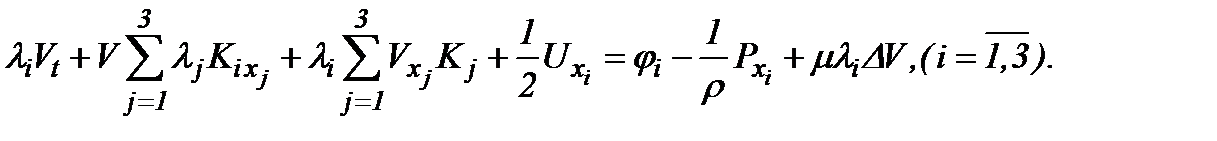                     (5.4)

Значит, на основании (5.4) имеем

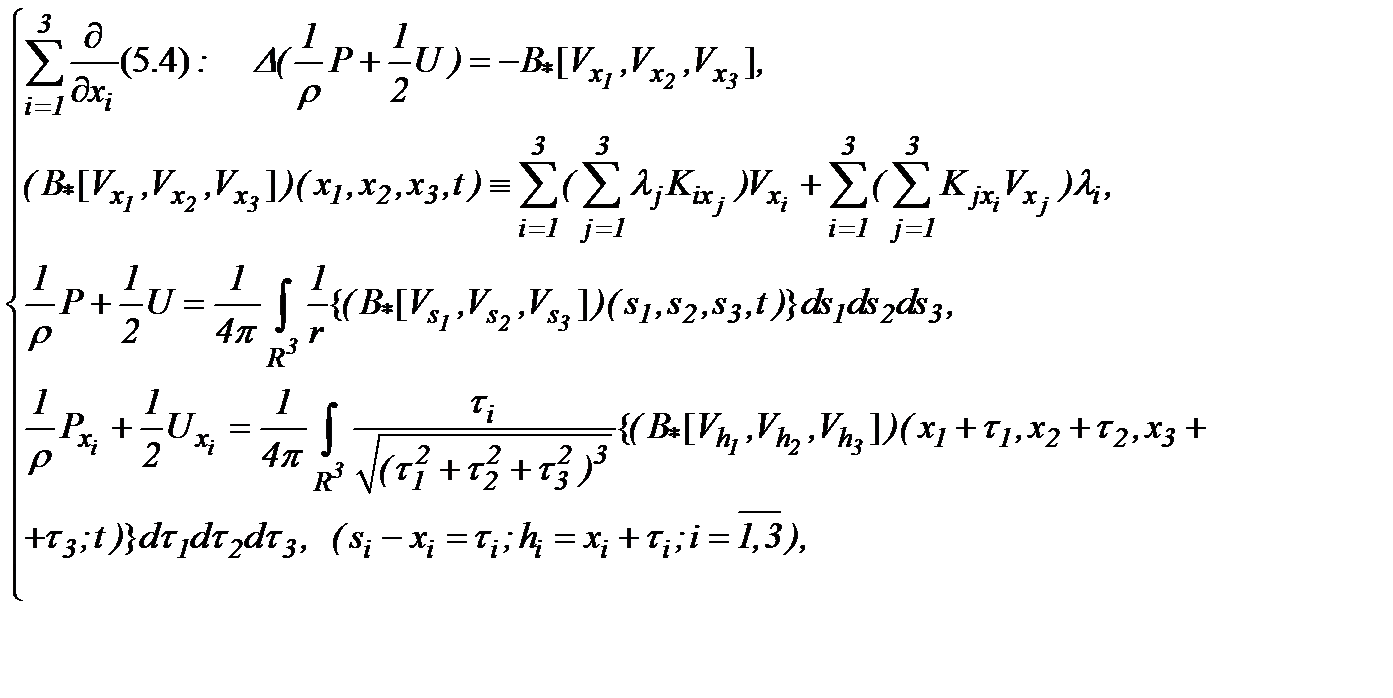          (5.5)

так как имеет место

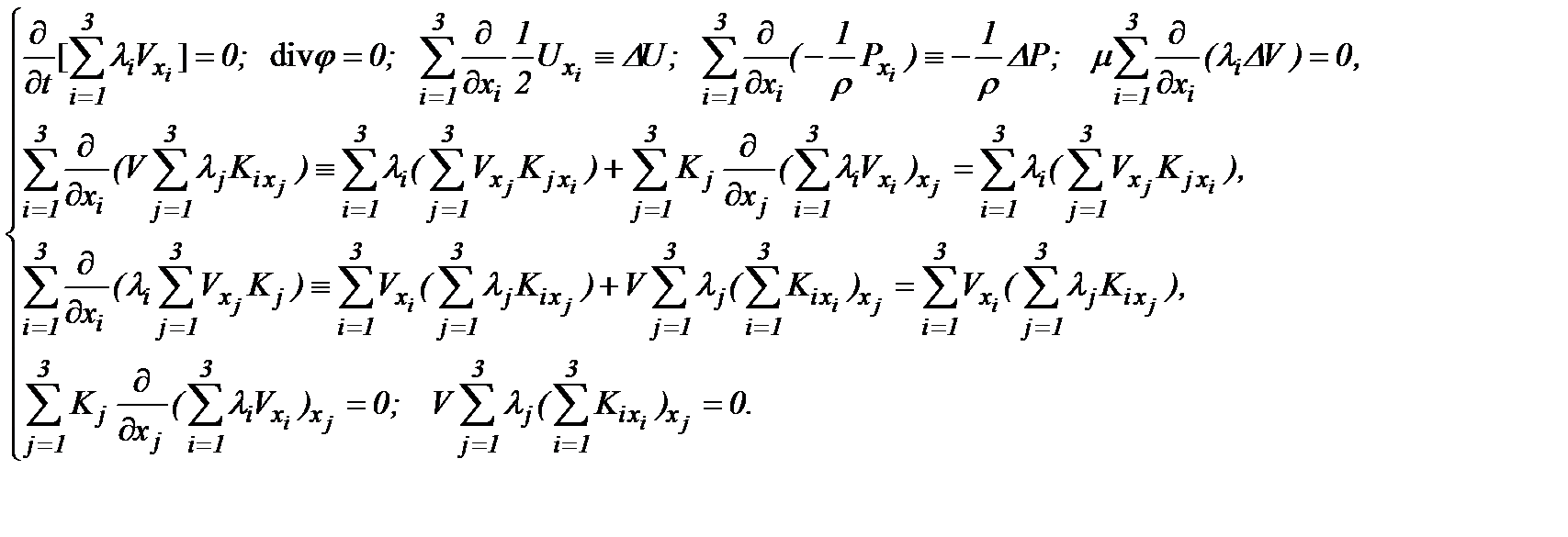
Тогда систему (5.4) можно эквивалентно преобразовать к виду

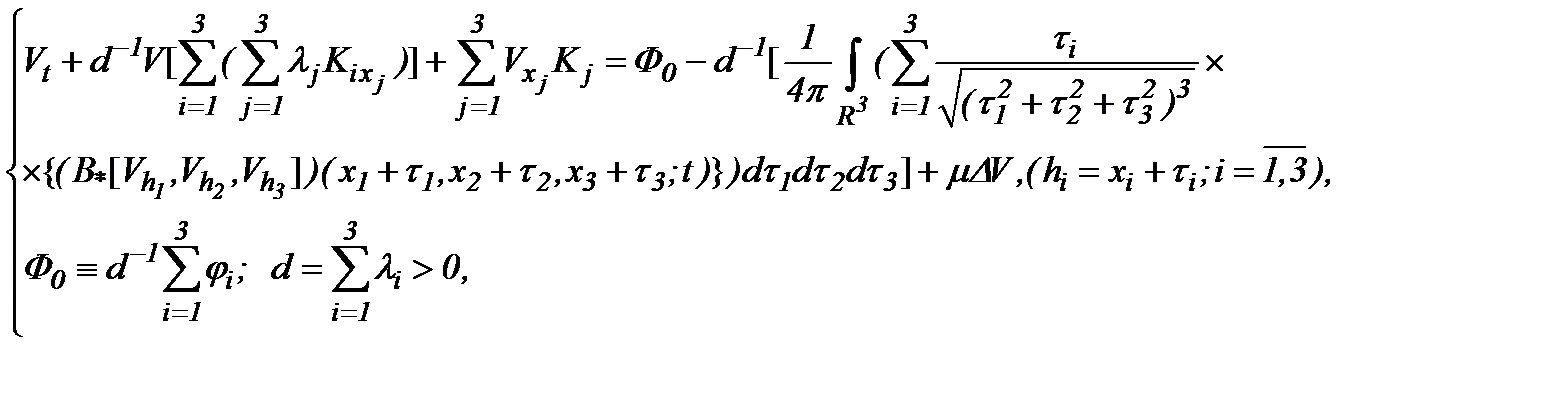   (5.6)

т.е. заменить одним уравнением с одной неизвестной 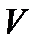. Следовательно, неизвестная функция  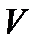определяется уравнением

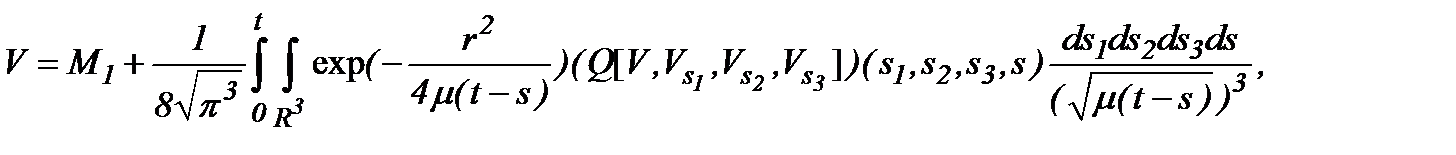           (5.7)

где

  

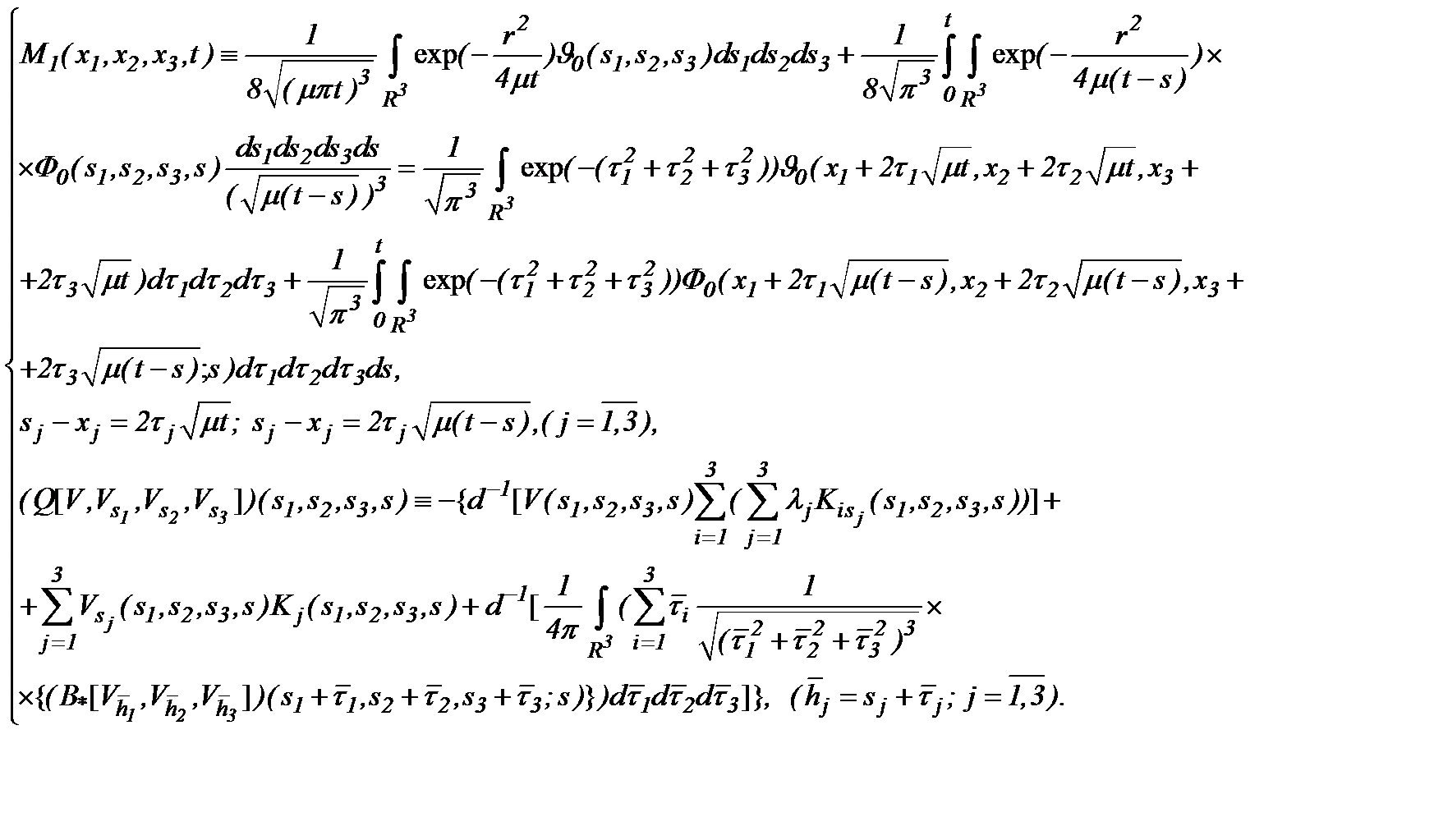
Уравнения (5.7) содержат неизвестные функции 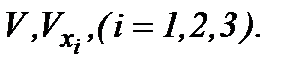 Дифференцируя (5.7) по  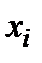и вводя обозначение  

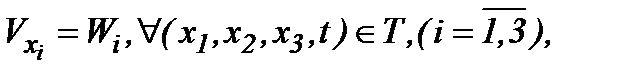                                                       (5.8)

преобразуем выражение (5.7) в систему

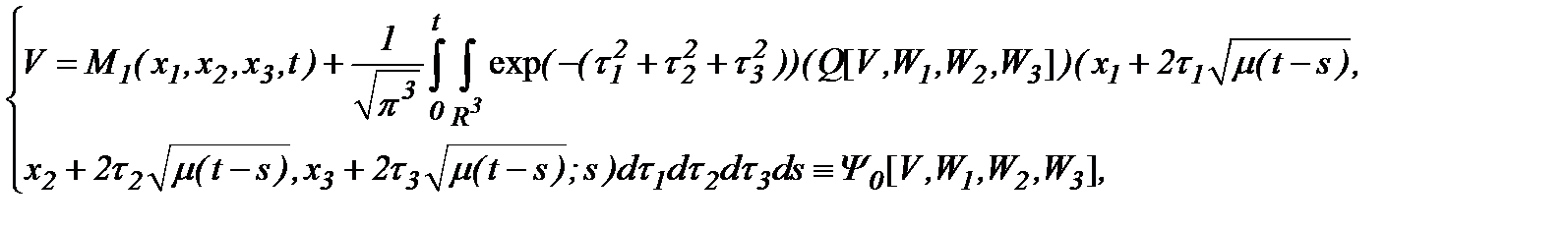
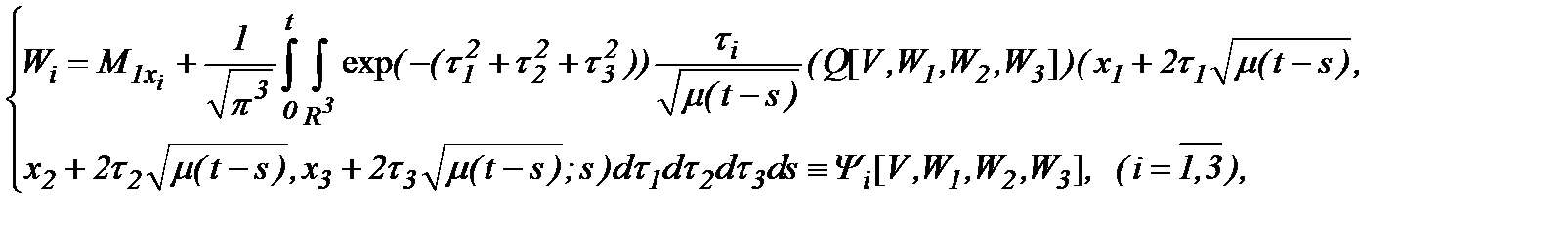(5.9)

которая (5.9) состоит из четырех интегральных уравнений 2-го рода по переменной 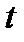 с четырьмя неизвестными функциями.

Для доказательства однозначной совместимости этой системы положим, что

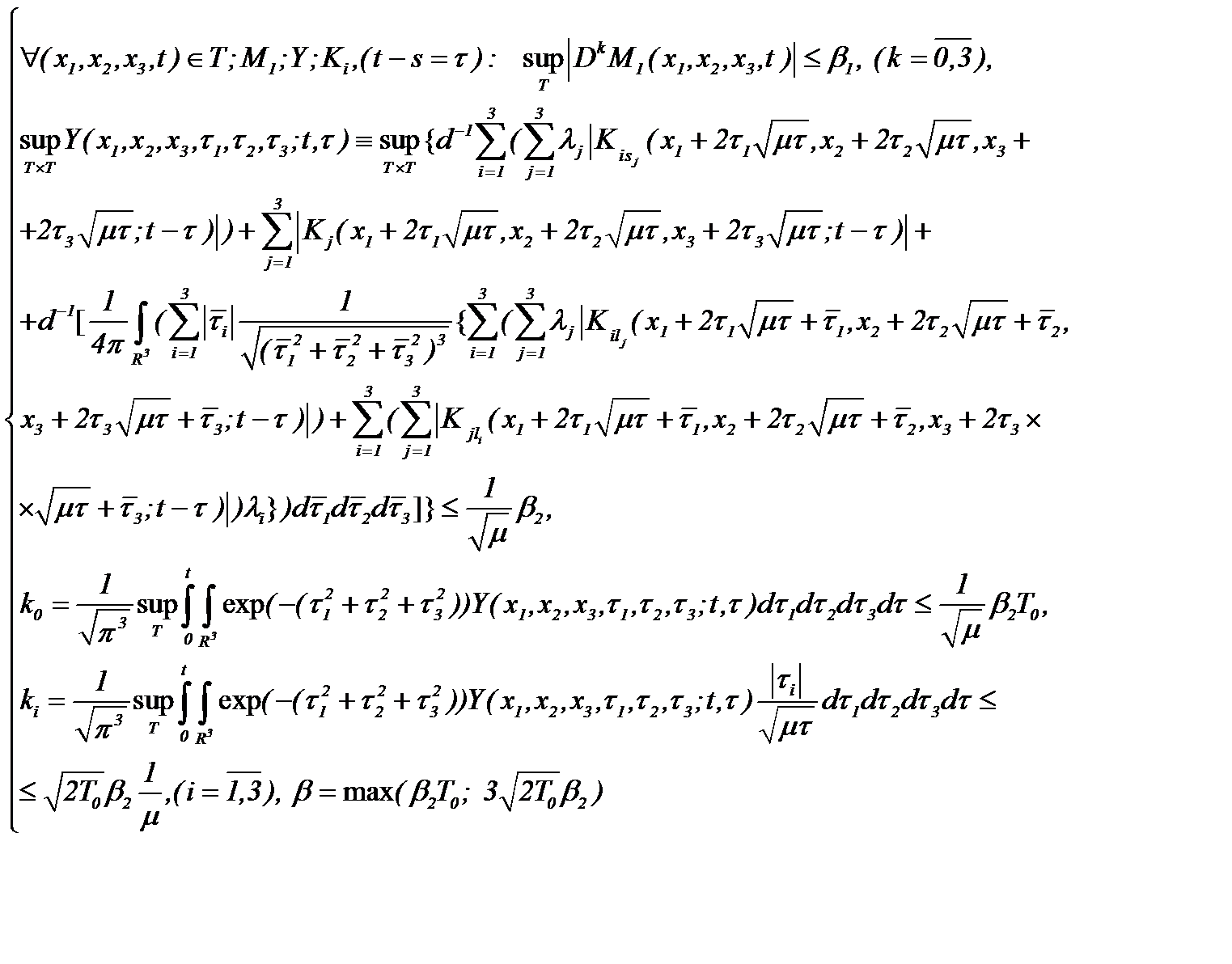(5.10)

 и

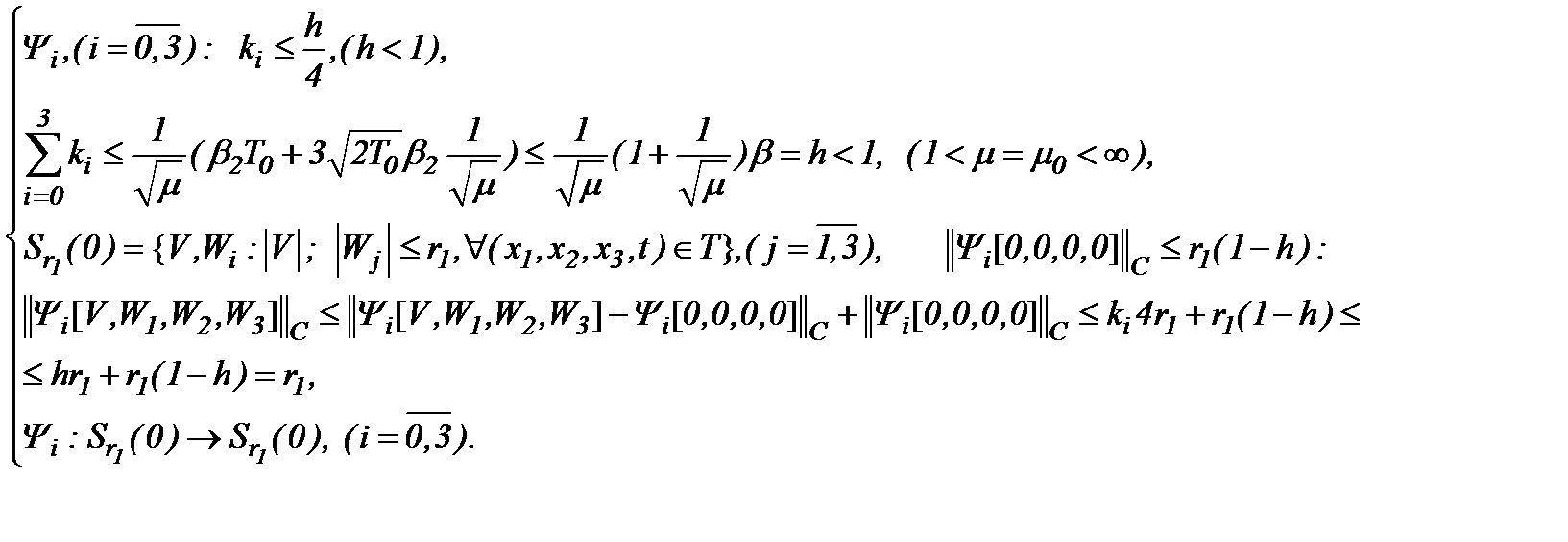(5.11)

Тогда решение (5.9) существует и единственно и его можно найти по методу Пикара

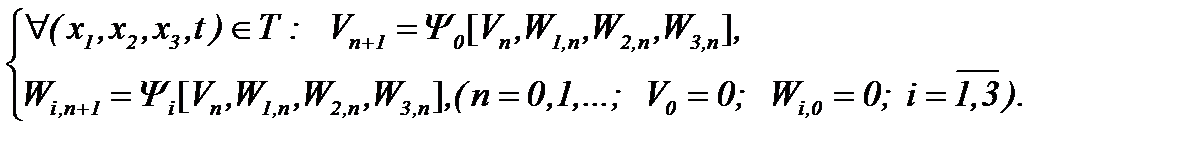                 (5.12)

Поэтому на основе математических выводов метода Пикара последовательности функций 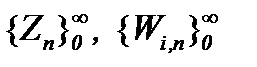 являются сходящимися и фундаментальными в 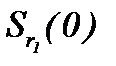, при этом, то, что элементы построенных последовательностей принадлежат  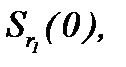доказывается на основе выражения (5.11). Значит, последовательности  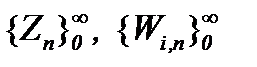сходятся к пределу 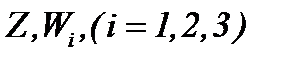, т.е.     

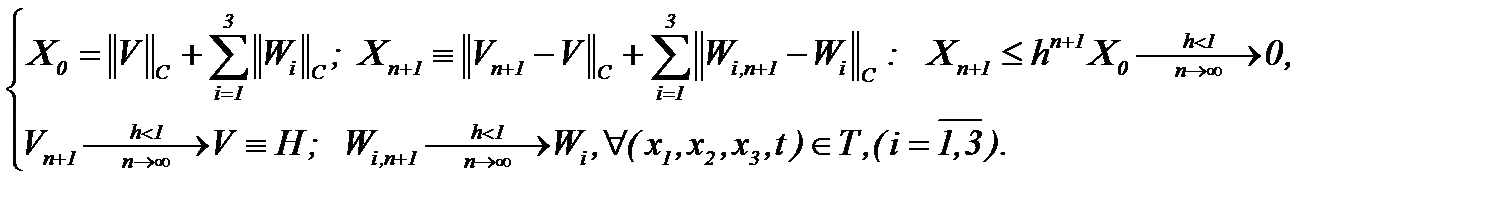  (5.13)

Тогда на основе правила (5.2), получим

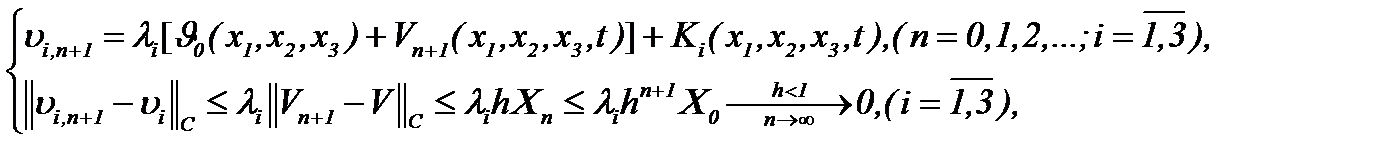        (5.14)

а это означает, что последовательности 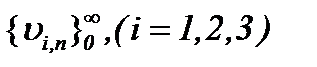 стремятся к пределу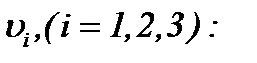  

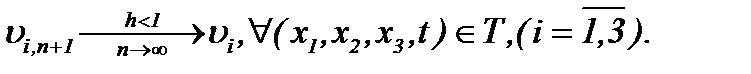                                           (5.15)

Теорема 6. Задача Навье-Стокса при условиях (1.2), (1.3), (5.1) и (5.15) имеет единственное непрерывное решение в 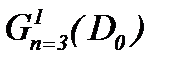, которое определяется с помощью правила (5.2).

Замечания:

I . Единственность очевидна на основе метода от противного. Результаты (5.13) с условиями (5.1), (5.10), (5.11) получены, когда гладкость функций до требуемого порядка требуется только по 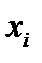, так как производная первого порядка по времени определяется для всех 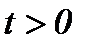. Тогда с учетом (5.13) система (5.9) имеет единственное непрерывное решение, а потому уравнение (5.7) имеет единственное решение  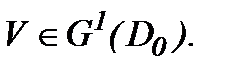Значит, на основе (5.2), (5.14) и (5.15)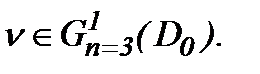   

II . Алгоритм (5.2) также справедлив в случае, если

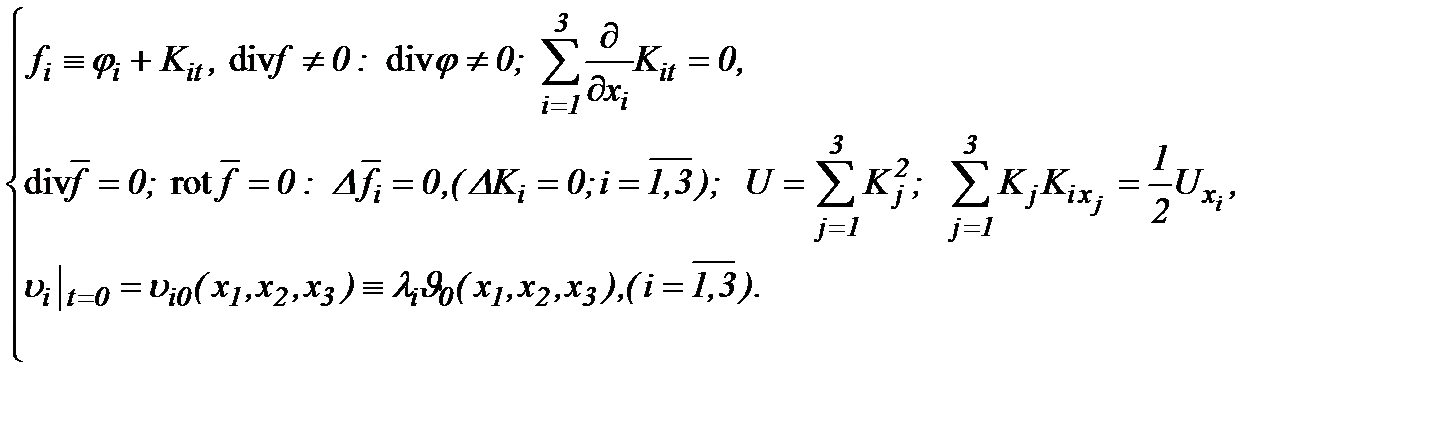    (5.16)

На основе (5.16) и (5.2) получим (5.4). Следовательно,

       

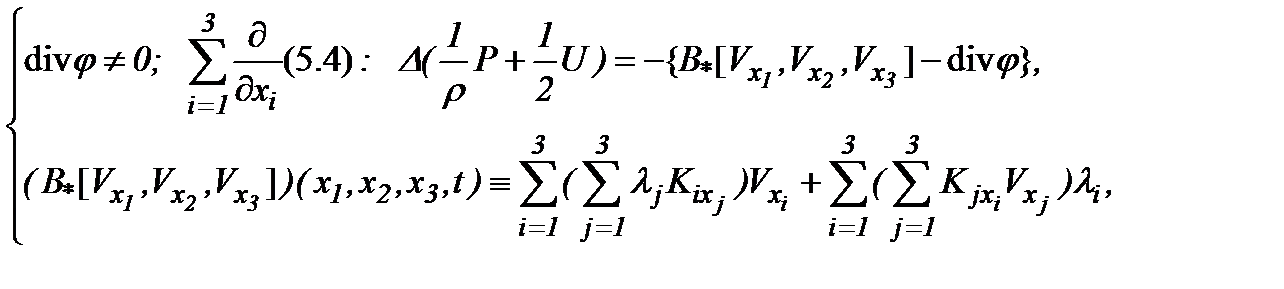
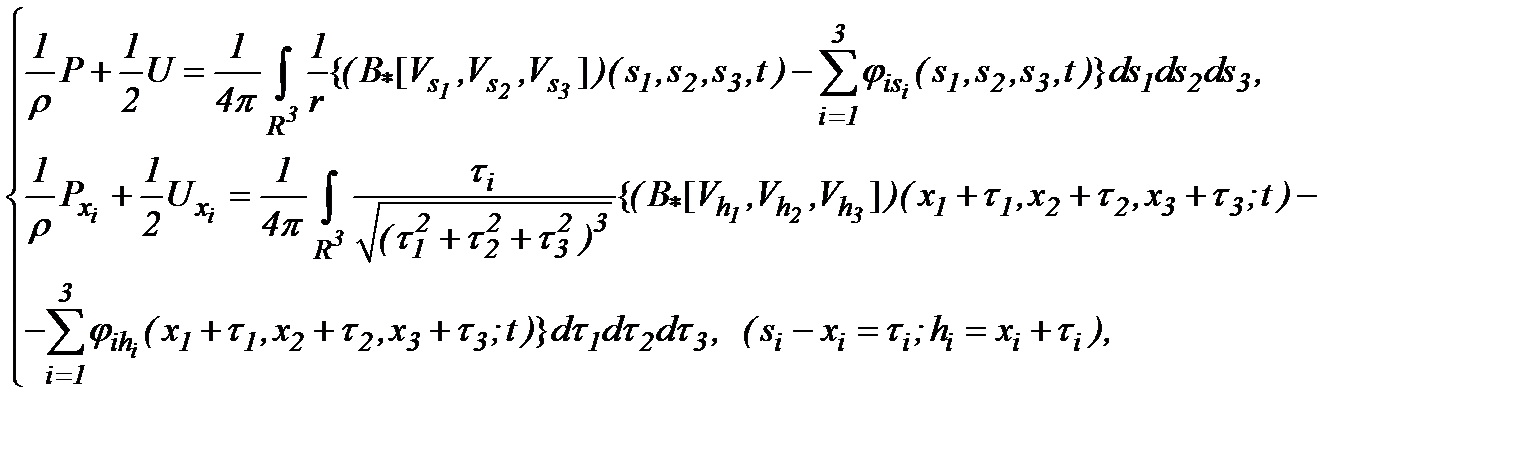  (5.17)

а поэтому имеет место

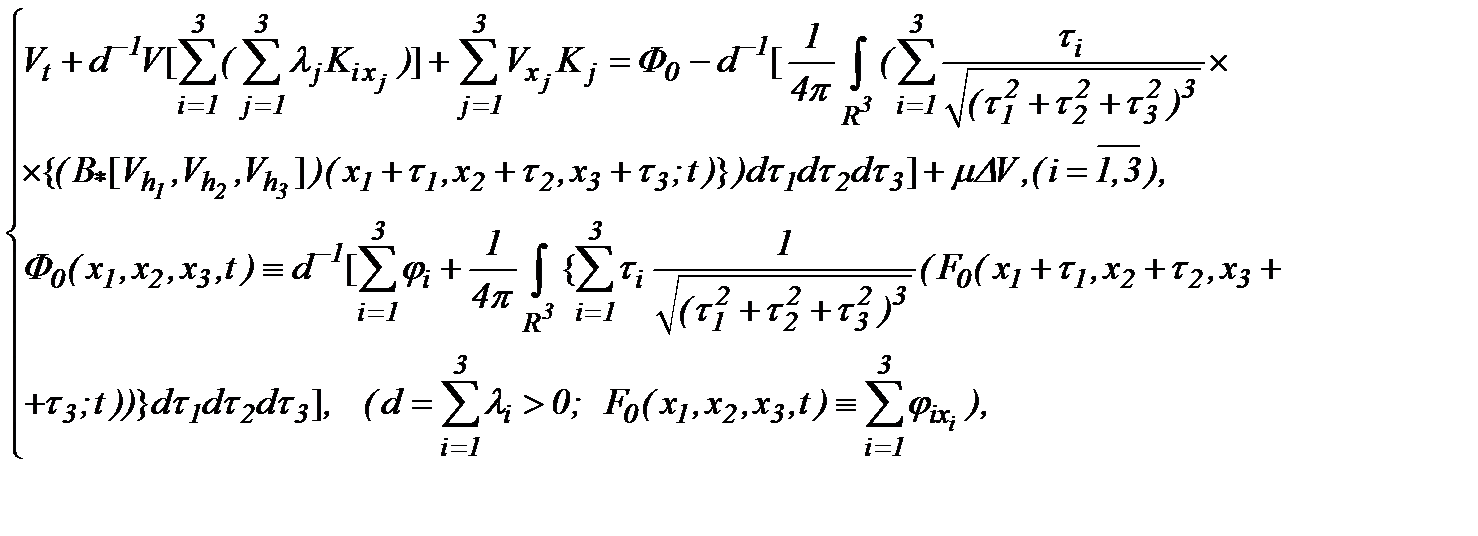    (5.18)

где выражение (5.17), как видно, отличается от (5.5), так как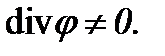  

Тогда с учетом (5.18), (5.7) и (5.8), получаем систему (5.9)

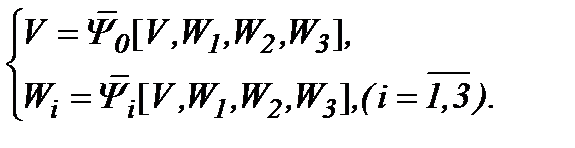                                                     (5.19)

Относительно трансформированной системы (5.19), требуя выполнения условий (5.10), (5.11), (5.13), как следствие (5.14), получим  

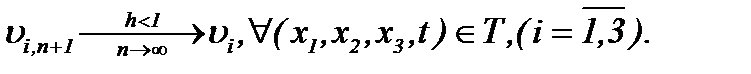                                                       (5.20)

Значит, получен результат, аналогичный результату теоремы 6, что и требовалось доказать.