

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Интересное:
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
5.2. Модификация метода (5.2), когда 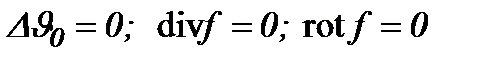
В данном пункте рассматривается модификация метода (5.2), необходимая для интегрирования уравнений Навье-Стокса в классе функций 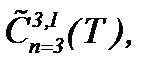 а именно в случае, когда
а именно в случае, когда
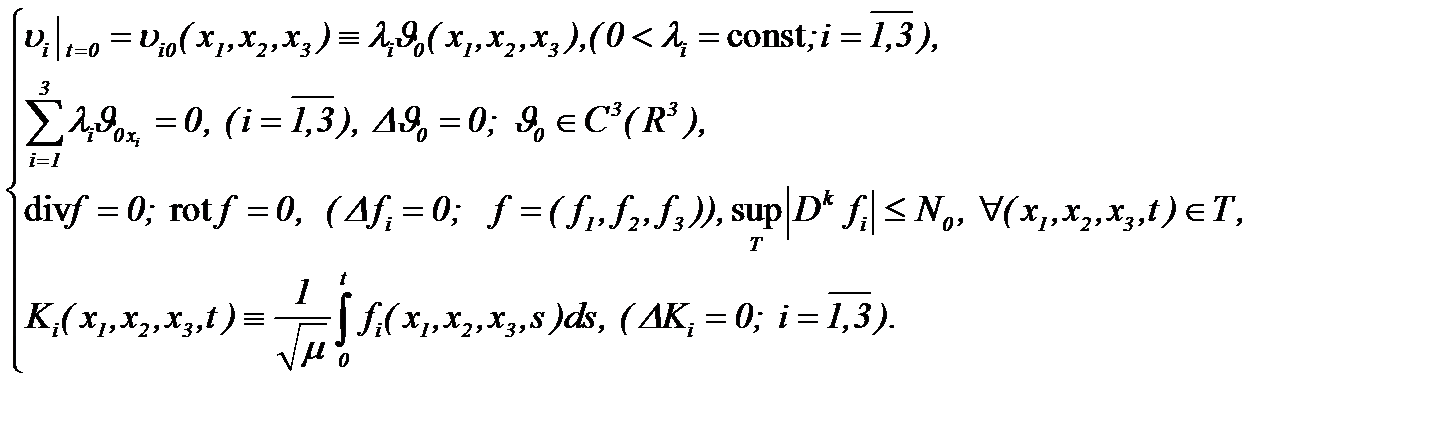 (5.21)
(5.21)
Поэтому, как и ранее, компоненты скоростей определяем по правилу
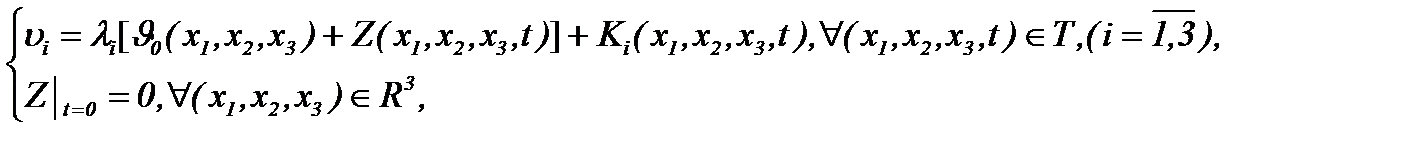 (5.22)
(5.22)
причем
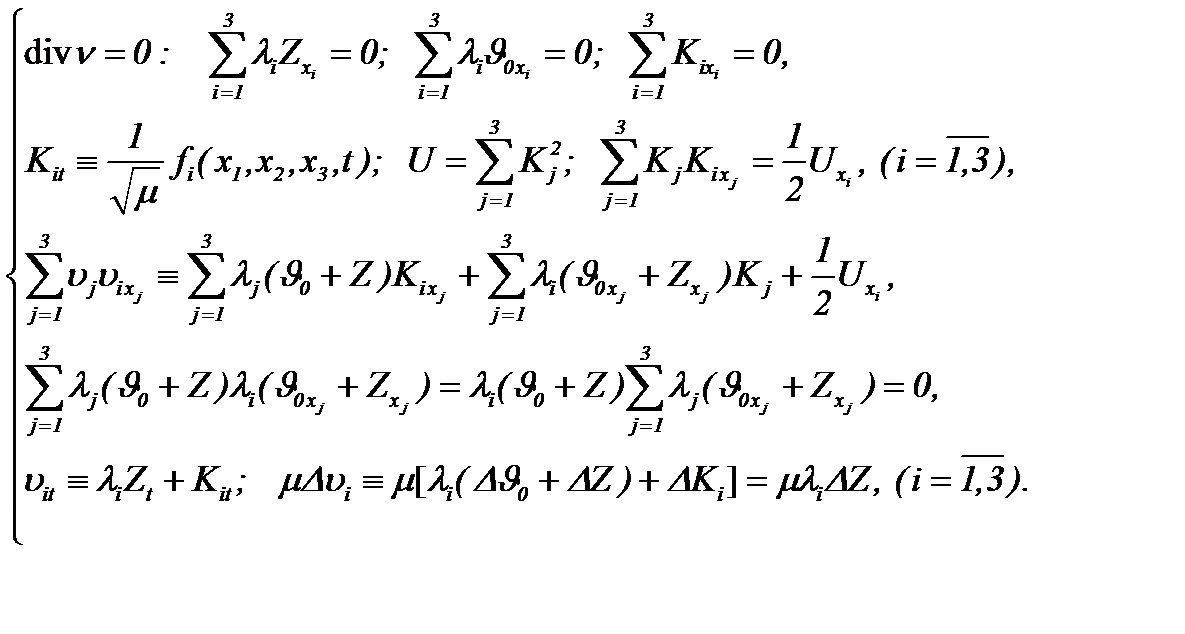 (5.23)
(5.23)
Следовательно, на основании (5.21) – (5.23) система (1.1) преобразуется к виду
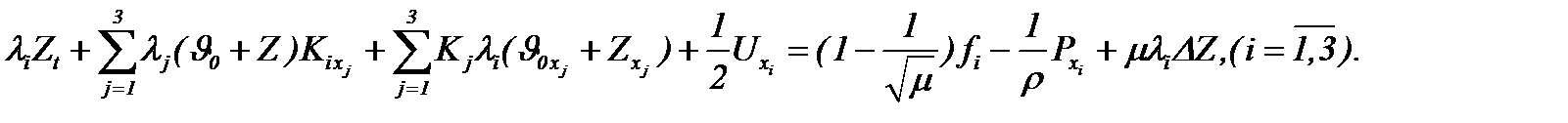 (5.24)
(5.24)
Поэтому, принимая во внимание результаты предыдущего пункта, а именно (5.5) – (5.9), а
также то, что вместо 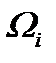 мы будем рассматривать
мы будем рассматривать 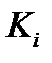 , из уравнения (5.24) получим
, из уравнения (5.24) получим
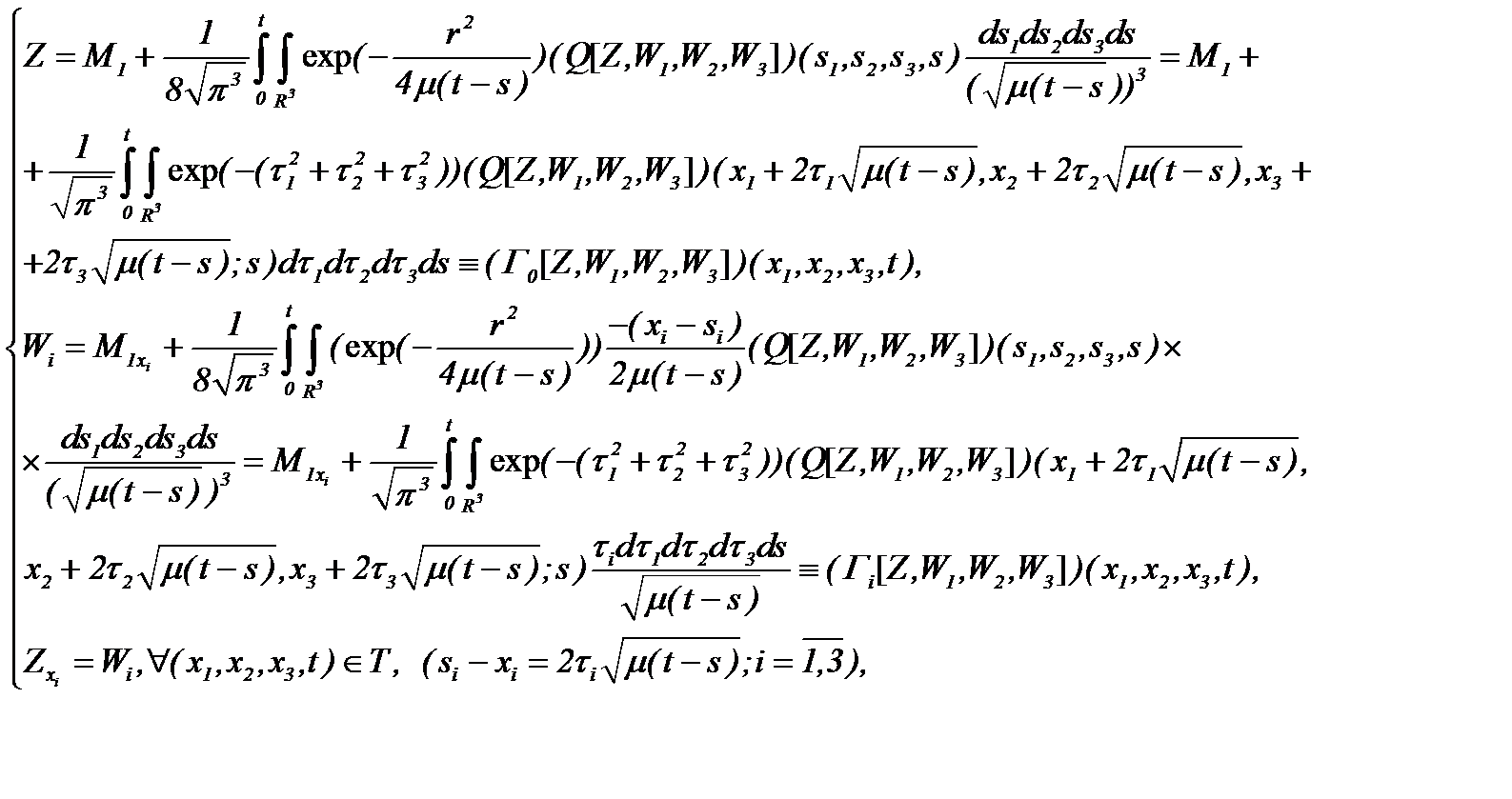 (5.25)
(5.25)
где
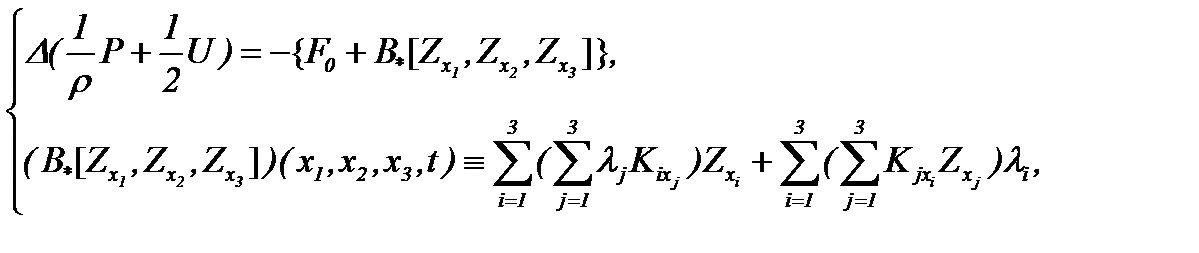
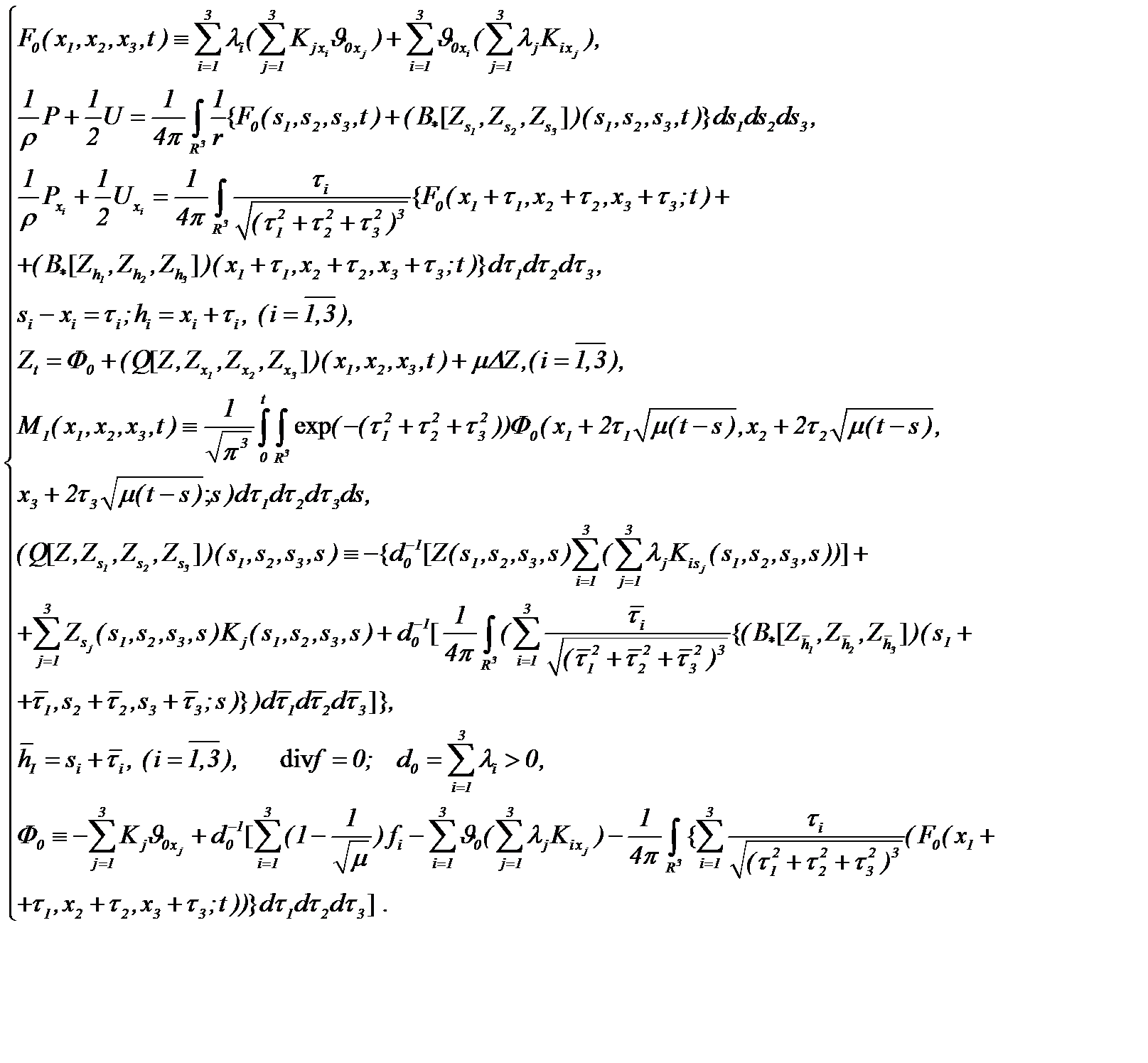 (5.26)
(5.26)
Теперь, пусть известные функции, входящие в систему (5.25), удовлетворяют условиям
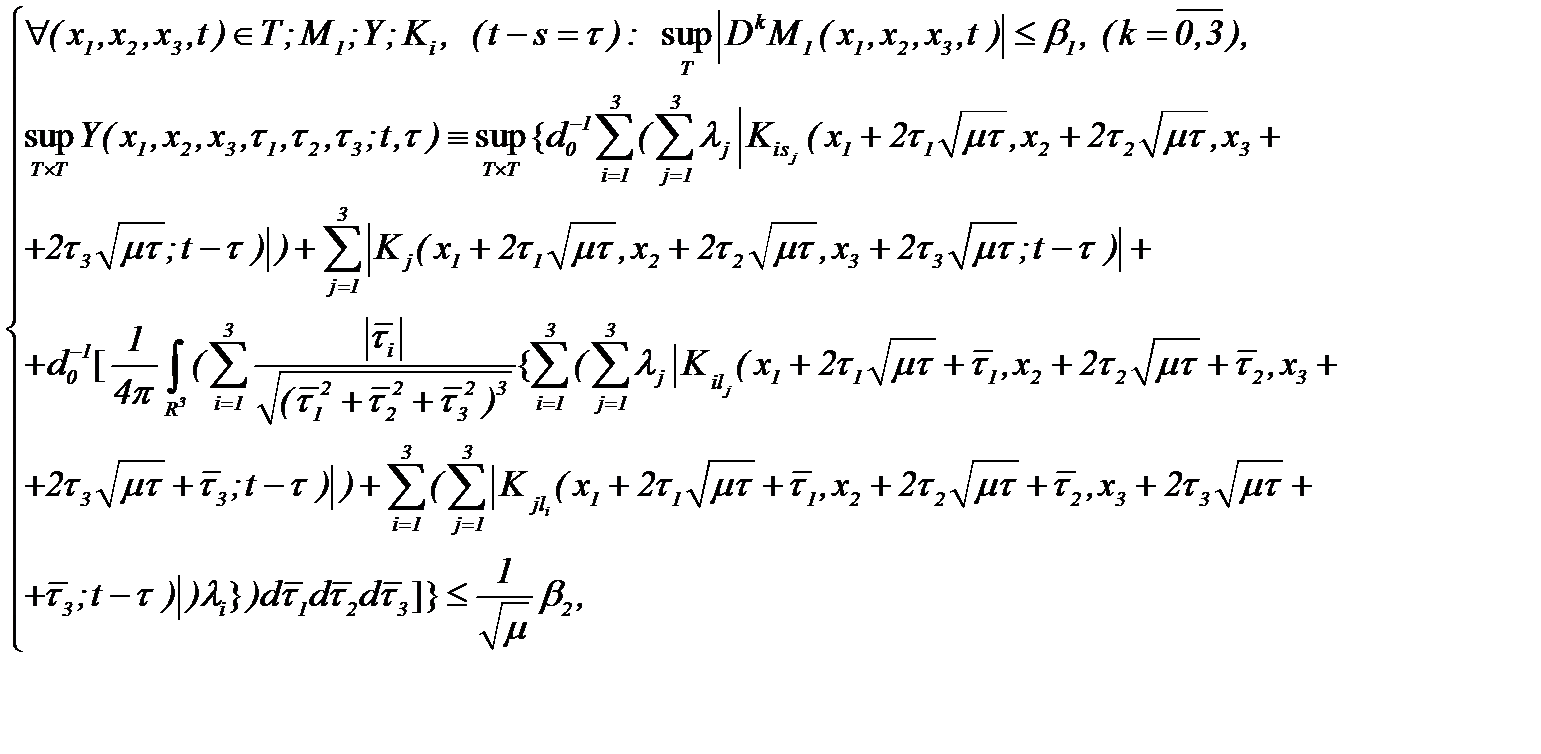
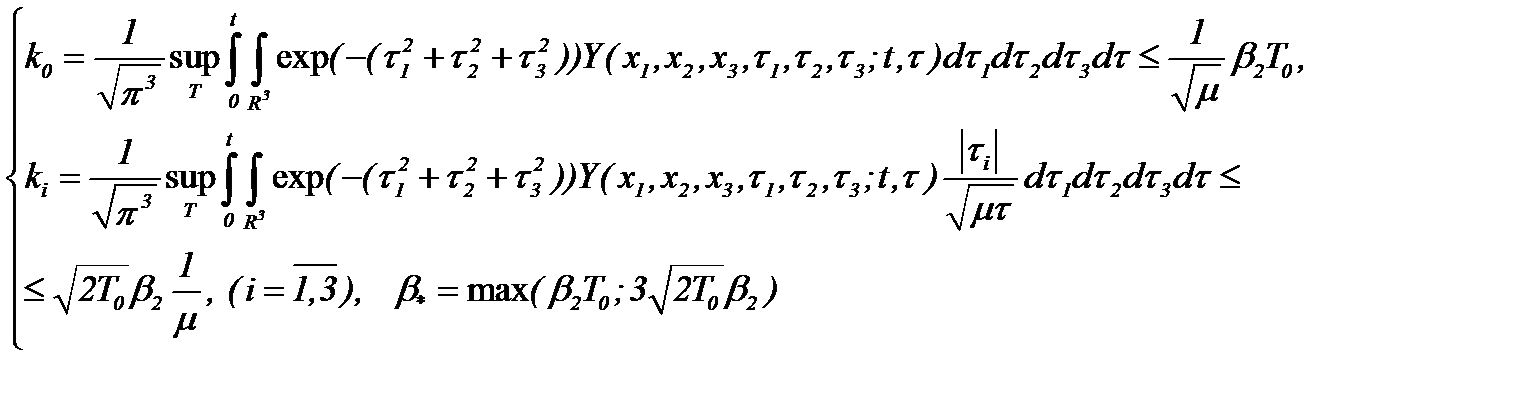 (5.27)
(5.27)
и
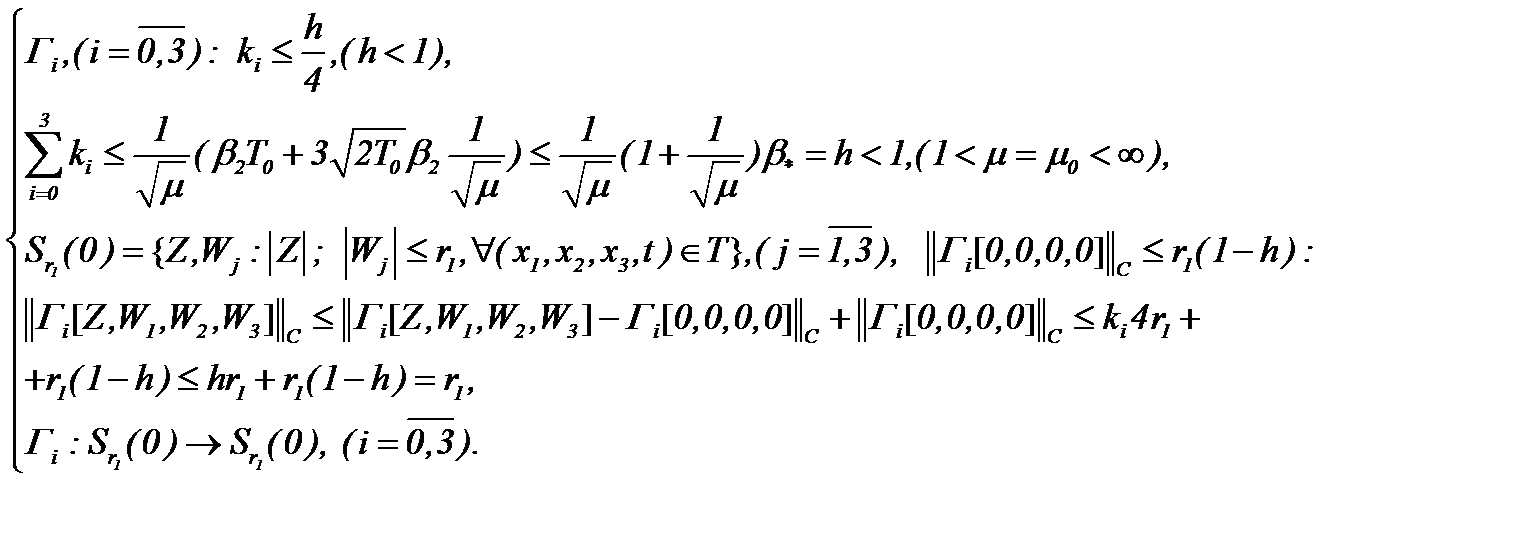 (5.28)
(5.28)
Тогда решение этой системы можем найти на основе метода Пикара
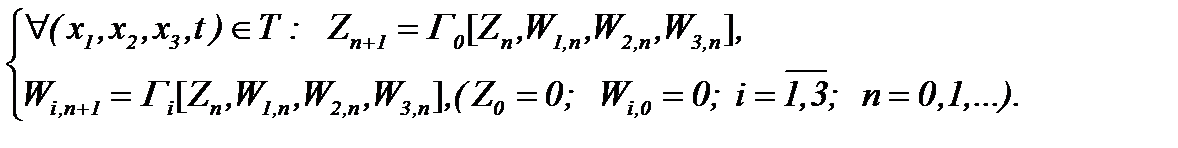 (5.29)
(5.29)
Отсюда следует, что с учетом результатов (5.13) – (5.15) получим, что последовательности функций 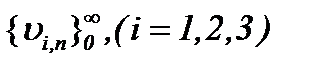 сходятся к пределу
сходятся к пределу 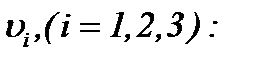
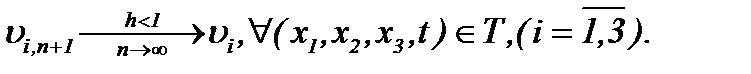 (5.30)
(5.30)
Теорема 6*. Если выполнены условия (1.2), (1.3), (5.21) – (5.23) и (5.30), то задача Навье-Стокса разрешима в 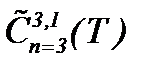 .
.
Замечание 6. При условии 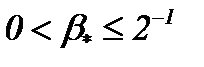 имеем
имеем 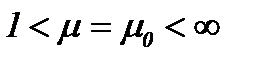 . Однако, если
. Однако, если 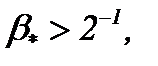 то
то
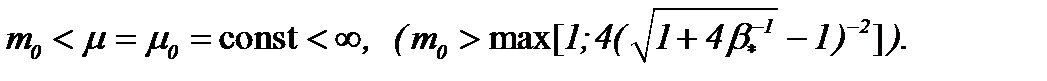 (1)*
(1)*
Если же 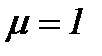 , причем
, причем
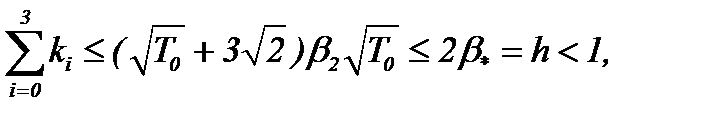 (см. (5.28)), (2)*
(см. (5.28)), (2)*
то, очевидно, задача Навье-Стокса разрешима в 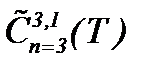 .
.
Отметим, так как уравнения системы ( 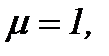 (5.25)) являются уравнениями Вольтерра-Абеля по переменной t, то обсуждая на языке уравнений Вольтерра, мы можем найти решение в
(5.25)) являются уравнениями Вольтерра-Абеля по переменной t, то обсуждая на языке уравнений Вольтерра, мы можем найти решение в
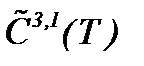 , т.е., как и в случае, когда условие (5.28) не выполнено. Поэтому предположим, что
, т.е., как и в случае, когда условие (5.28) не выполнено. Поэтому предположим, что
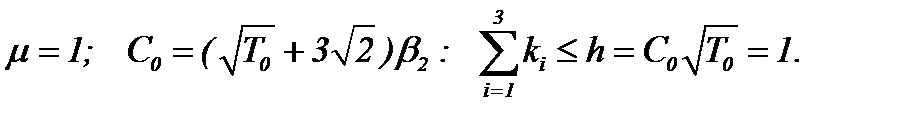 (3)*
(3)*
Тогда и в этом случае справедливы все результаты теоремы 4*, поэтому докажем, что при соблюдении условия (3)* система (5.25) имеет единственное решение в 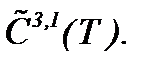
Для случая (3)* разделим интервал 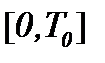 на две части:
на две части: 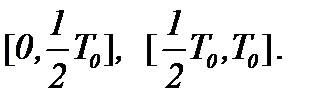 Как видно, шаг
Как видно, шаг 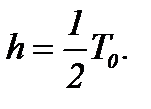 В итоге получили пару систем в областях
В итоге получили пару систем в областях 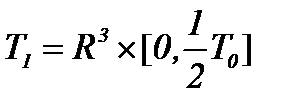 и
и 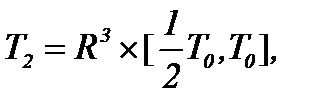 т.е.
т.е.
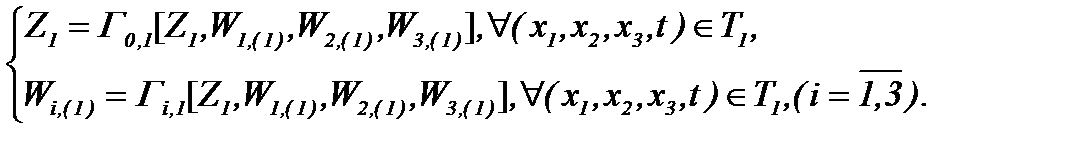 (4)*
(4)*
Тогда операторы 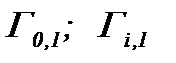 являются сжимающими с коэффициентом сжатия
являются сжимающими с коэффициентом сжатия
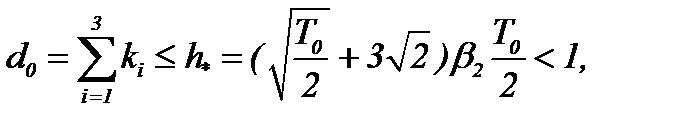 (5)*
(5)*
а, значит, отображают области определения в себя. Поэтому при соблюдении условия (5)* принцип сжатых отображений выполнен, а потому система (4)* разрешима в 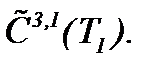
Далее рассмотрим 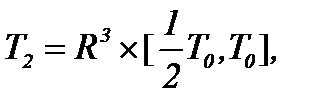 соответственно операторам
соответственно операторам 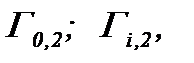 причем
причем
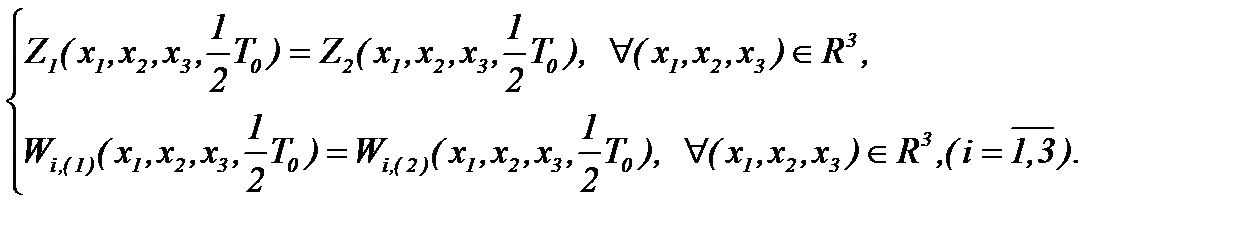 (6)* Если, как и ранее, операторы
(6)* Если, как и ранее, операторы 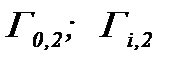 допускают сжатие отображений, то система интегральных уравнений с указанными операторами разрешима в
допускают сжатие отображений, то система интегральных уравнений с указанными операторами разрешима в 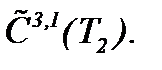 Значит, система (5.25) корректна в
Значит, система (5.25) корректна в 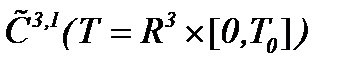 . В теории уравнений Вольтерра предлагаемый метод решения системы (5.25) называется «методом склеивания» или «методом подобластей».
. В теории уравнений Вольтерра предлагаемый метод решения системы (5.25) называется «методом склеивания» или «методом подобластей».
|
|
|

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...
© cyberpedia.su 2017-2025 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!