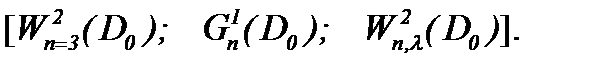7.3. Жидкость с вязкостью, когда 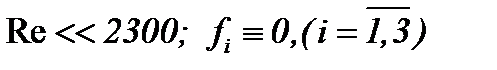
Обобщим результаты пункта 5.3 относительно задачи Коши для однородных nD уравнений Навье-Стокса со средним и небольшим числом Рейнольдса. При этом ставим задачу: найти для метода (7.14) такую модификацию, чтобы получить аналитическое решение задачи Навье-Стокса в 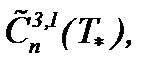 когда
когда
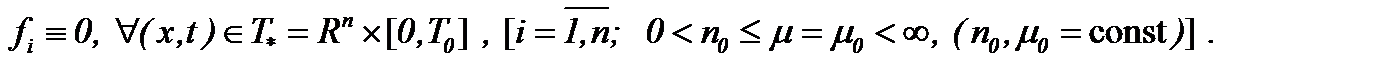 (7.21)
(7.21)
Задача (1.1)n – (1.3)n с условием (7.21) принимает следующий вид
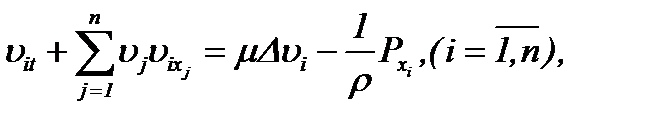 (7.22)
(7.22)
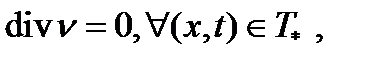 (7.23)
(7.23)
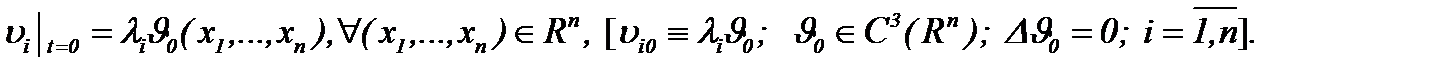 (7.24)
(7.24)
Для полученной задачи рассмотрим метод интегрирования уравнений Навье-Стокса (7.22) с условиями (7.23), (7.24) в 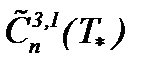 .
.
На основании ранее приведенных результатов будем считать, что существуют функции 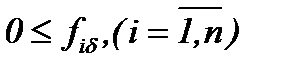 , которые удовлетворяют условиям
, которые удовлетворяют условиям
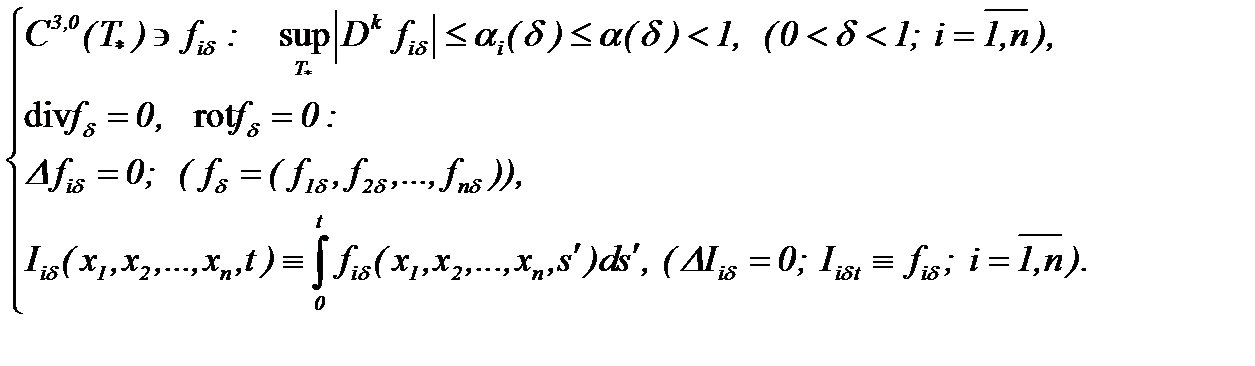 (7.25)
(7.25)
Тогда получаем преобразование в виде
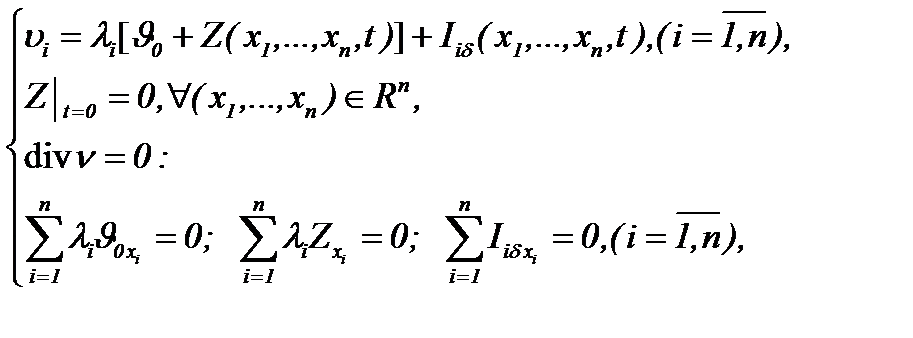 (7.26)
(7.26)
причем имеют место следующие условия
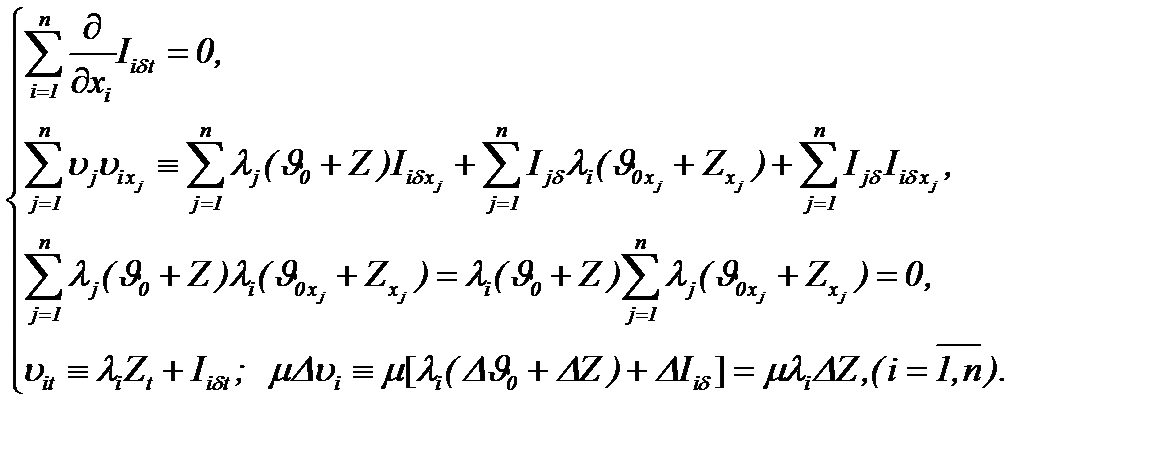 (7.27)
(7.27)
Поэтому на основе (7.26), задача (7.22) – (7.24) сводится к виду
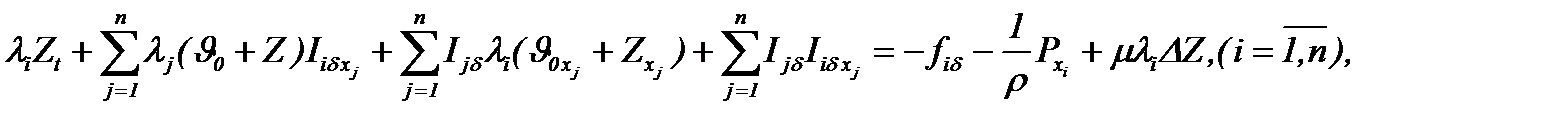 (7.28)
(7.28)
т.е. система Навье-Стокса (7.22) для несжимаемых течений с трением трансформируется в линейную систему (7.28).
Далее, из системы (7.28), учитывая условия (7.22)-(7.24) и применяя АПС, получим уравнение
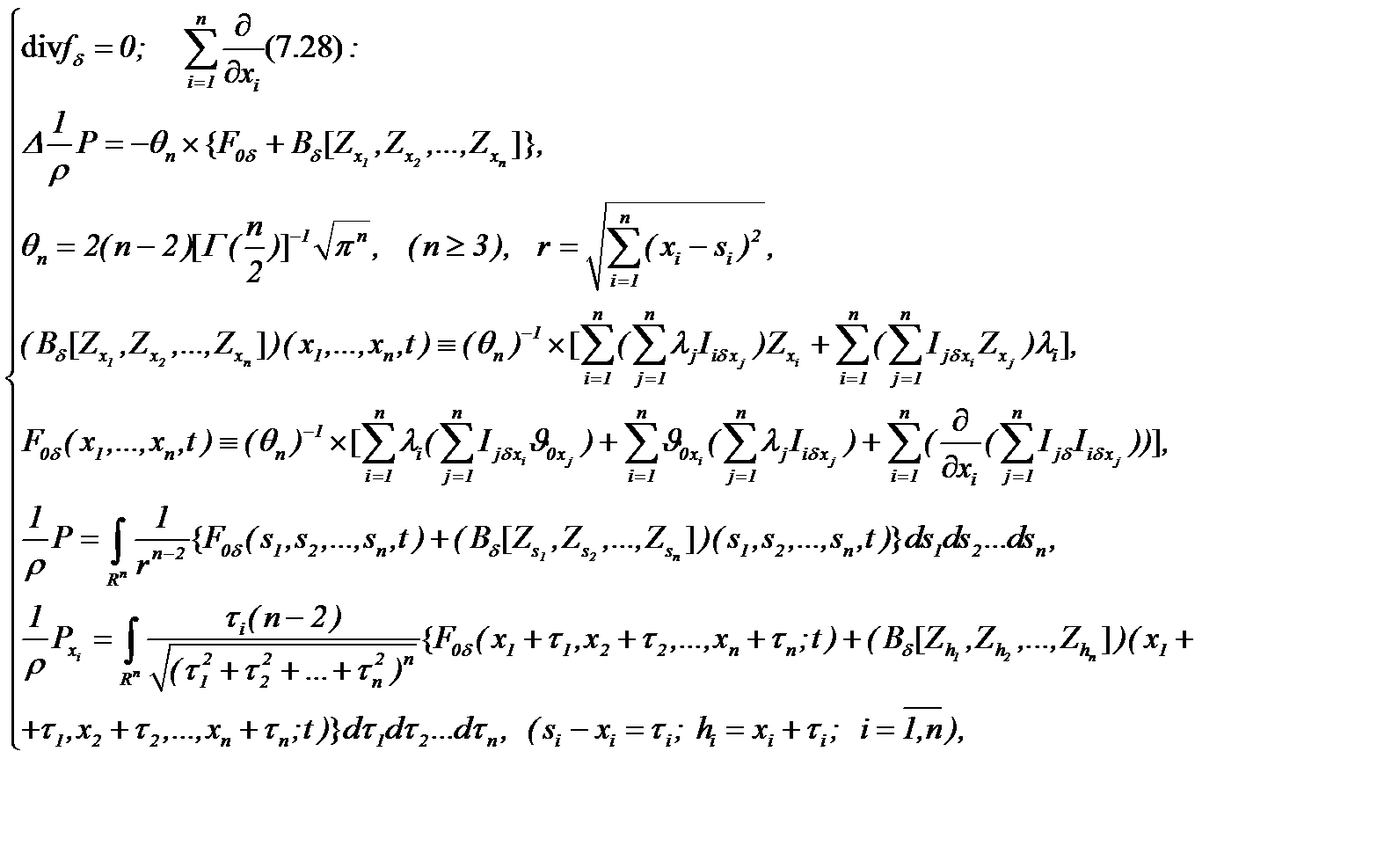 (7.29)
(7.29)
так как имеет место
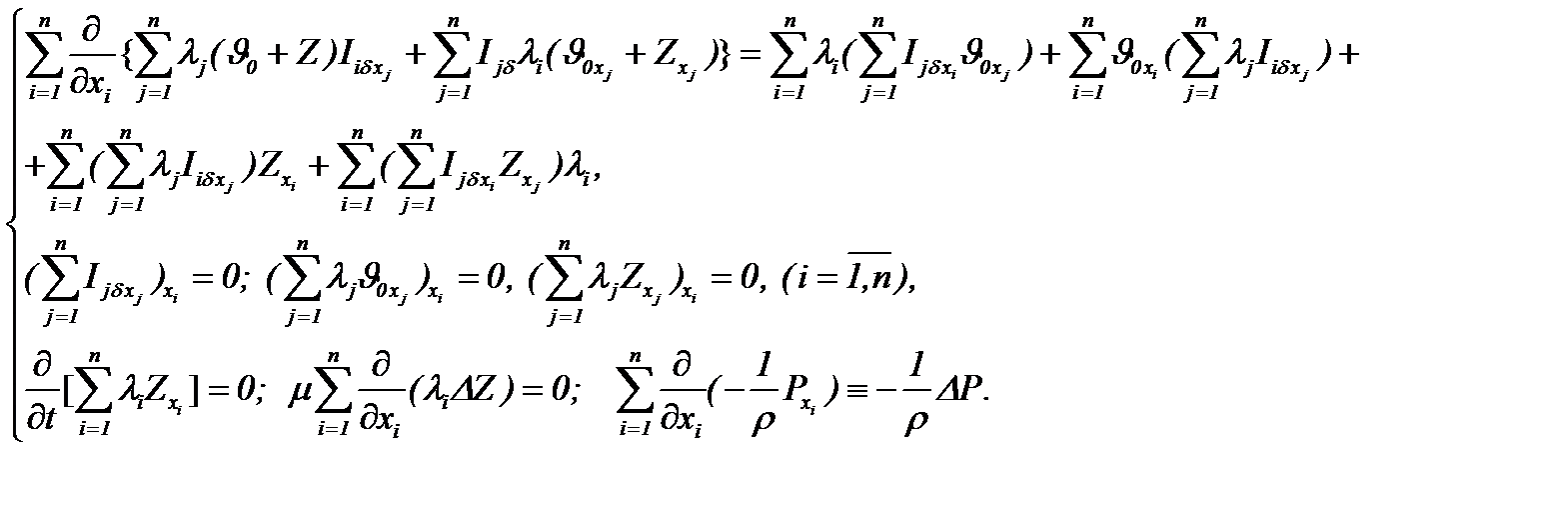
Поэтому на основании (7.29), система (7.28) эквивалентно преобразуется к виду
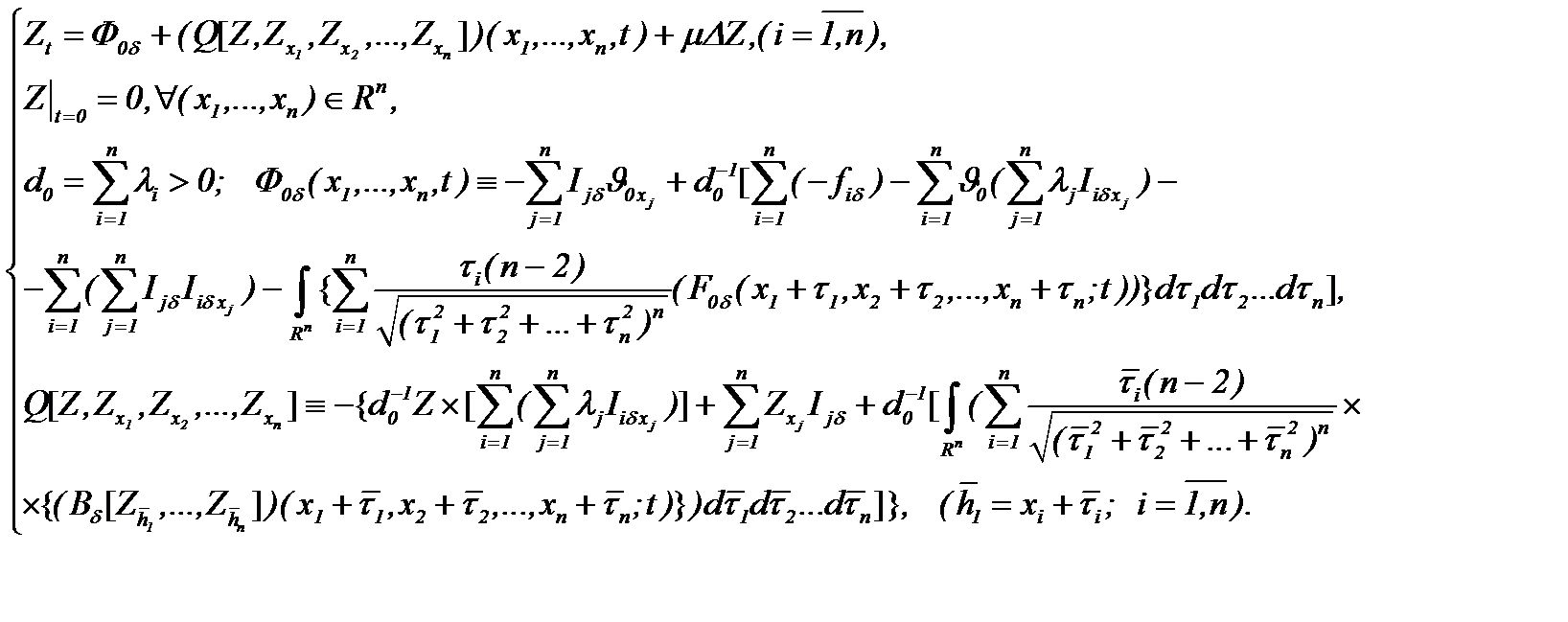 (7.30)
(7.30)
Таким образом, задача (7.30) сведена к следующей системе интегральных уравнений
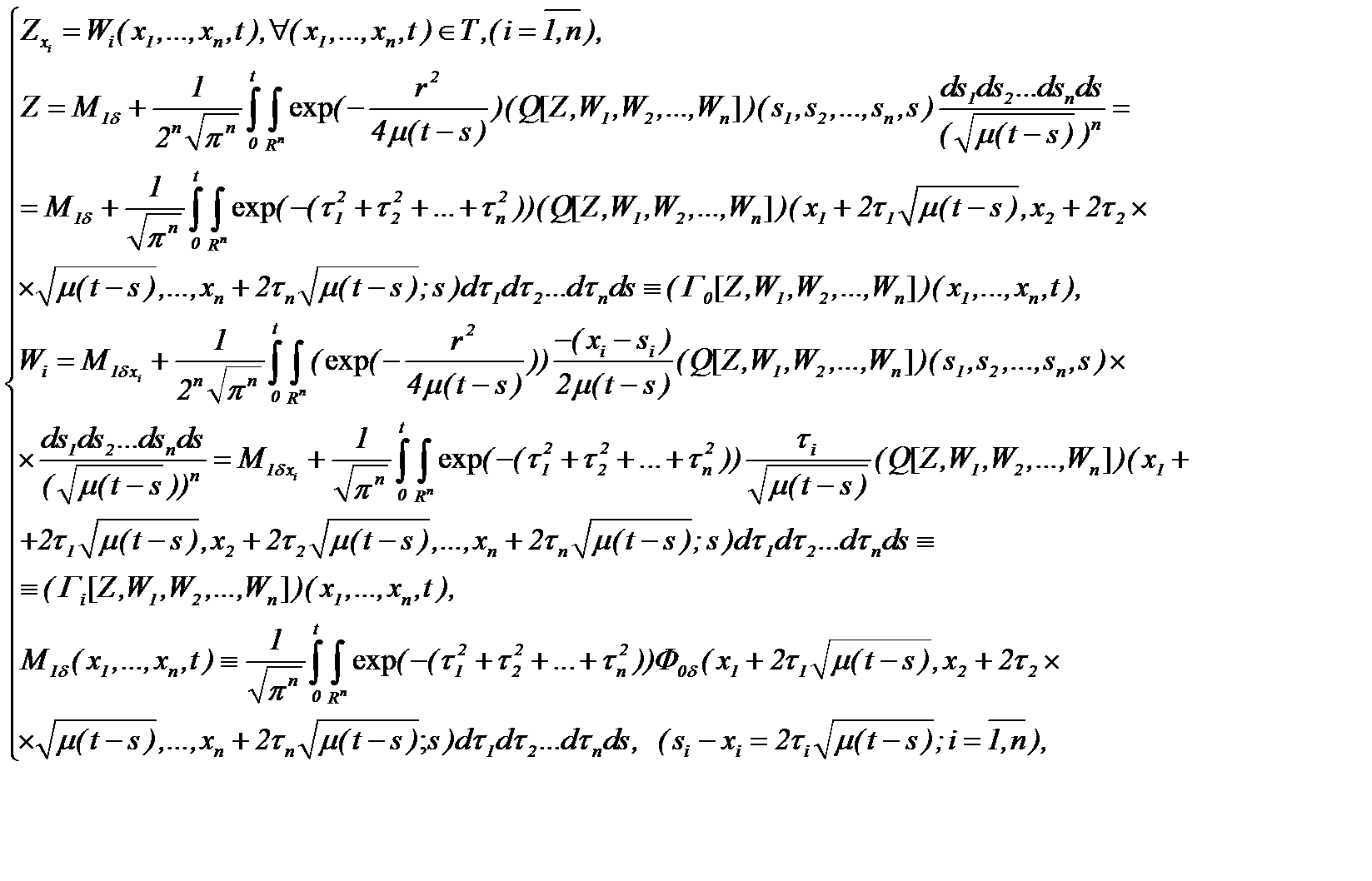 (7.31)
(7.31)
значит, для решения задачи (7.30) получена система (7.31) из « 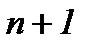 » интегральных уравнений с «
» интегральных уравнений с « 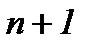 » неизвестными.
» неизвестными.
Для доказательства разрешимости системы (7.31) положим, что относительно известных
функций 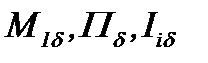 имеет место:
имеет место:
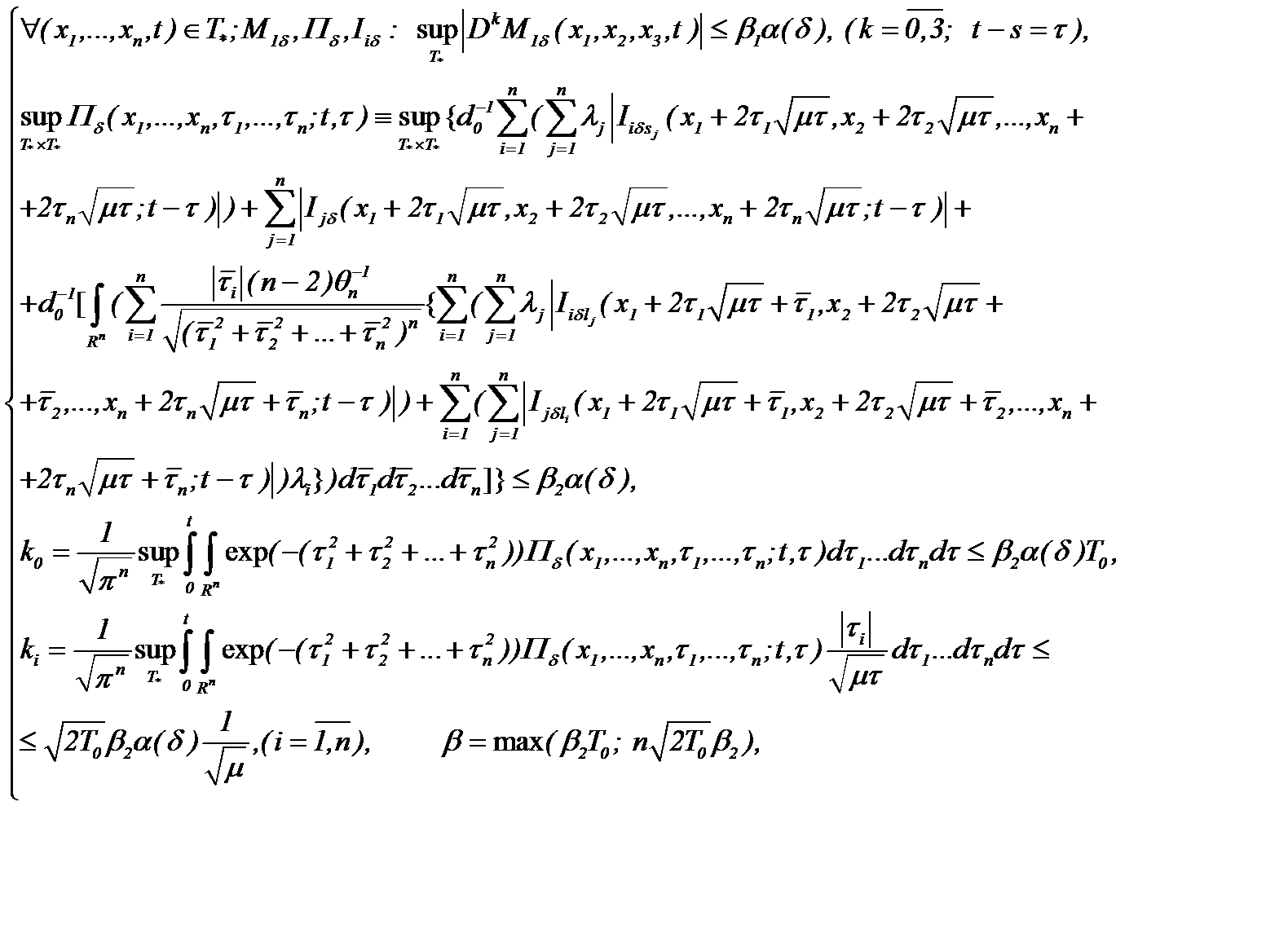 (7.32)
(7.32)
где операторы 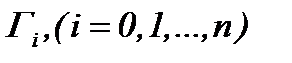 допускают сжатие отображений
допускают сжатие отображений
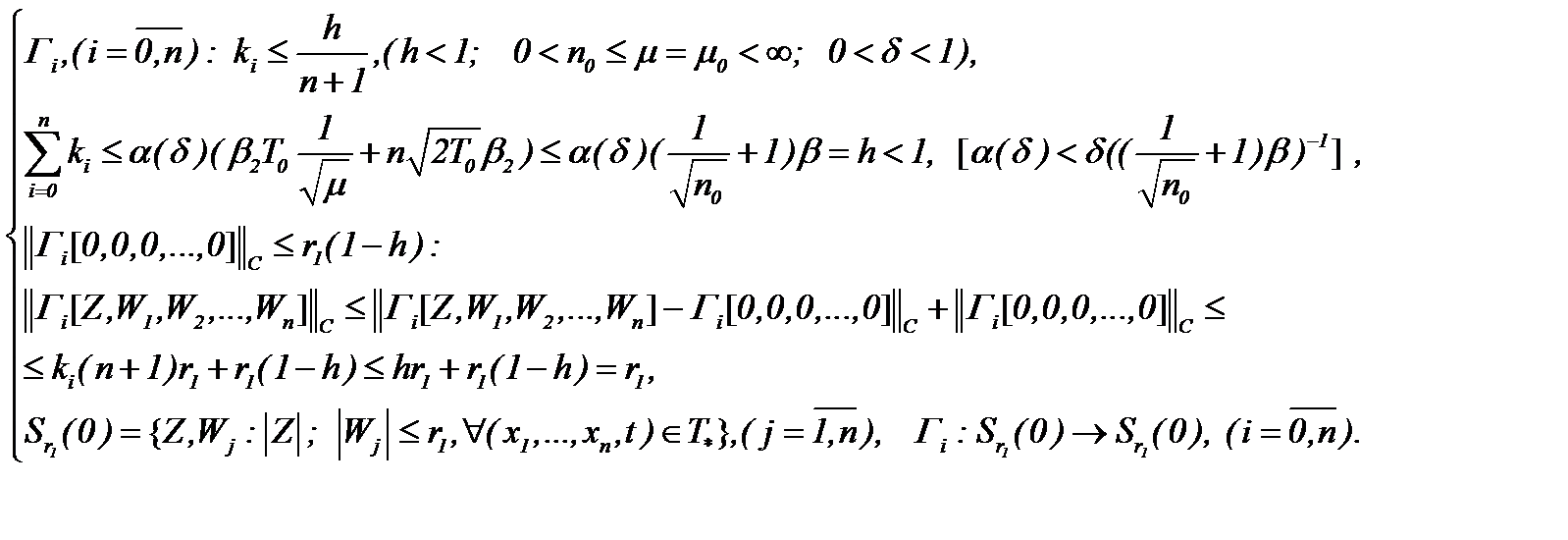 (7.33)
(7.33)
Тогда на основе принципа сжимающих отображений система (7.31) однозначно разрешима и для построения решения применим метод Пикара
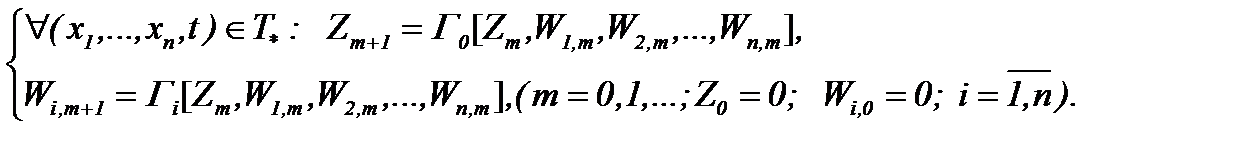 (7.34)
(7.34)
Значит, с учетом всех выводов метода Пикара имеем последовательности функций 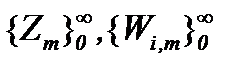 , которые являются сходящимися и фундаментальными в
, которые являются сходящимися и фундаментальными в  так как
так как
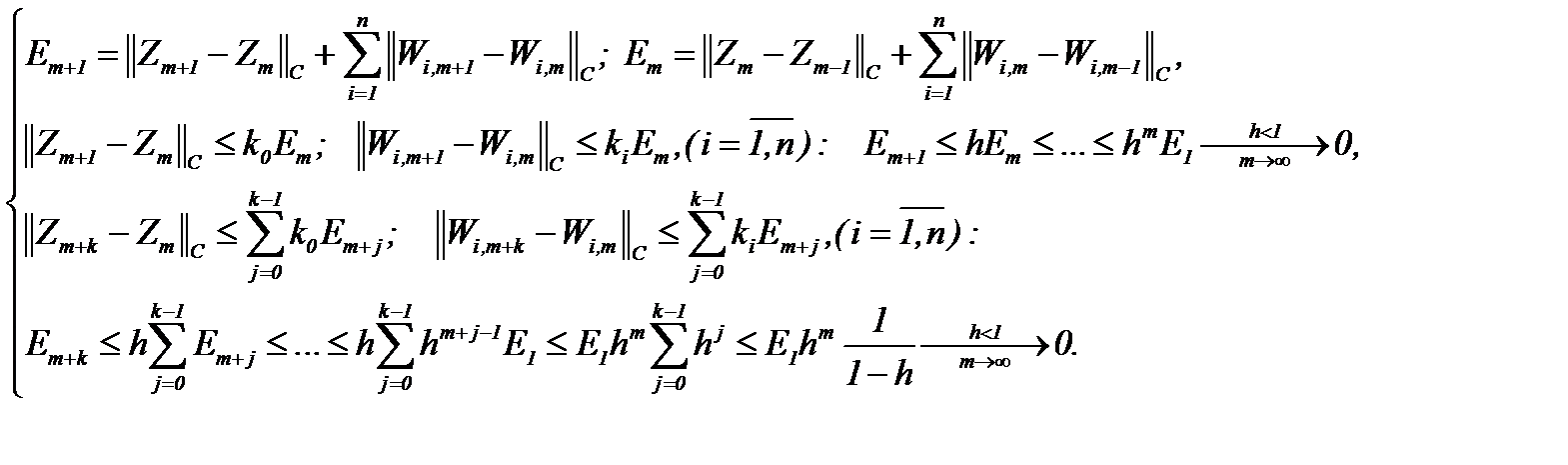
Следовательно,
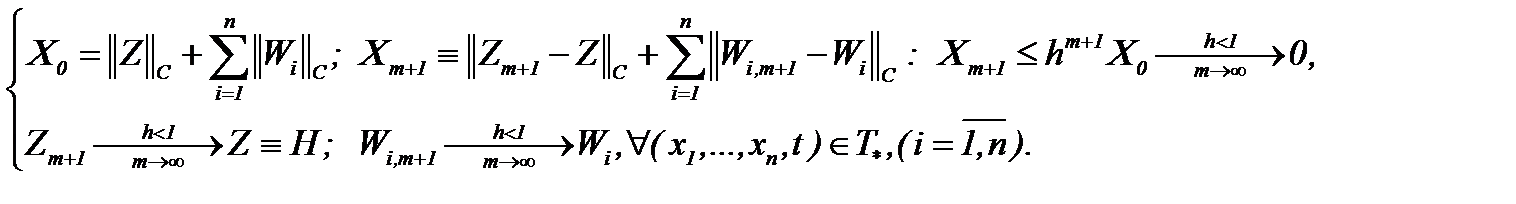 (7.35)
(7.35)
Поэтому на основании (7.26) получим оценку
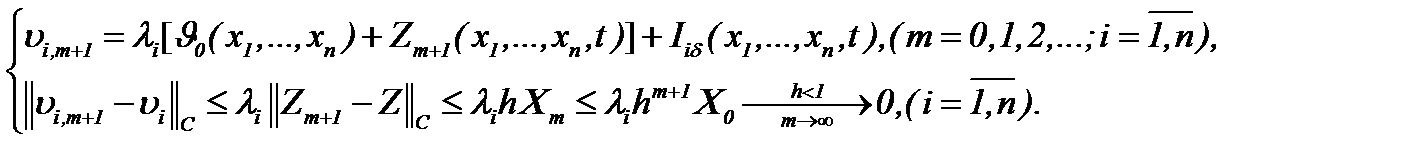 (7.36)
(7.36)
Это означает, что последовательности 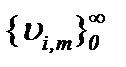 стремятся к пределу
стремятся к пределу 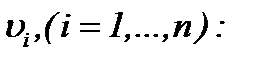
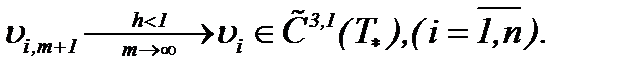 (7.37)
(7.37)
Теорема 9. Если выполняются условия (7.23), (7.24), (7.25), (7.32), (7.33) и (7.37), то задача Навье-Стокса корректна в 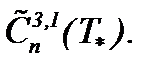
Доказательство. Действительно, при указанных условиях задача Навье-Стокса эквивалентно трансформируется в систему из « 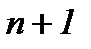 » интегральных уравнений с «
» интегральных уравнений с « 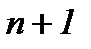 » неизвестными функциями, а, тем самым, для этой системы реализуются все условия принципа сжатых отображений. Тогда система (7.31) корректно поставлена в
» неизвестными функциями, а, тем самым, для этой системы реализуются все условия принципа сжатых отображений. Тогда система (7.31) корректно поставлена в 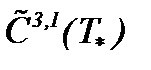 , то есть на основе (7.35) существует гладкая и единственная функция
, то есть на основе (7.35) существует гладкая и единственная функция 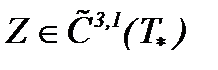 . Поэтому с учетом (7.26) при условиях (7.23), (7.24), (7.25), (7.32), (7.33) и (7.37) получим
. Поэтому с учетом (7.26) при условиях (7.23), (7.24), (7.25), (7.32), (7.33) и (7.37) получим 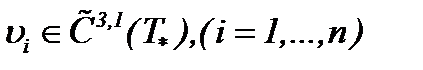 .
.
Очевидно, что малые изменения 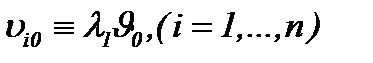 или
или 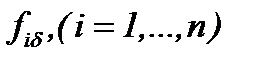 незначительно влияют на решение (7.26), то есть решение непрерывно зависит от этих данных. Поэтому, вопрос о корректности задачи (7.22) – (7.24) разрешается на основе результатов теоремы 9 в
незначительно влияют на решение (7.26), то есть решение непрерывно зависит от этих данных. Поэтому, вопрос о корректности задачи (7.22) – (7.24) разрешается на основе результатов теоремы 9 в 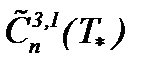 , что и требовалось доказать. ■
, что и требовалось доказать. ■
8. Заключение
Суть данной работы заключается в том, что разработанные аналитические методы решения без привлечения дополнительных условий эквивалентно преобразуют задачу Навье-Стокса (1.1) – (1.3) в неоднородные линейные уравнения типа теплопроводности с условием Коши, которые, как известно, разрешимы в классе функций с достаточно гладкими начальными условиями в момент времени 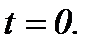 Поэтому преобразованные задачи сохраняют математические и физические закономерности постановки исходной задачи и значения переменных, отвечающих требованиям Математического Института Клея.
Поэтому преобразованные задачи сохраняют математические и физические закономерности постановки исходной задачи и значения переменных, отвечающих требованиям Математического Института Клея.
В работе [8] исследована задача Навье-Стокса с вязкостью в неограниченной области, а именно тот вариант, который предпочтительнее по сравнению с другими вариантами проблемы тысячелетия. Задача, трансформированная с помощью математических преобразований:
а) имеет строгое гладкое аналитическое решение, или
б) имеет аналитическое решение, основанное на методе Пикара.
В настоящем исследовании результаты работы [8] развиты для 3D и nD уравнений Навье-Стокса вязкой несжимаемой жидкости. В параграфе 4 полученные результаты иллюстрируются примером в ограниченной области.
Решение шестой проблемы тысячелетия связано с критерием регулярности Билла-Като-Мажда [2, 5]. Впервые этот критерий выведен для 3D уравнений Эйлера в статье [2], но в данной работе получено доказательство для 3D уравнений Навье-Стокса. Тем самым, рассматриваемый критерий обобщен для вязкой несжимаемой жидкости в 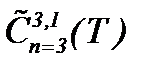 , где, относительно параметра вязкости, условие регулярности интегралов выражается в терминах времени интегрируемости. Когда аналитическое решение 3D уравнений Навье-Стокса удовлетворяет условия критерия Билла-Като-Мажда, то автоматически доказываются условия критерия и для 3D уравнений
, где, относительно параметра вязкости, условие регулярности интегралов выражается в терминах времени интегрируемости. Когда аналитическое решение 3D уравнений Навье-Стокса удовлетворяет условия критерия Билла-Като-Мажда, то автоматически доказываются условия критерия и для 3D уравнений
Эйлера, так как значение вязкости 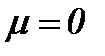 отвечает уравнению идеальной жидкости.
отвечает уравнению идеальной жидкости.
Таким образом, полученные в настоящей работе результаты отражают все требования шестой проблемы тысячелетия [1], а именно, задача Навье-Стокса (1.1) – (1.3), во-первых, имеет гладкое единственное решение в 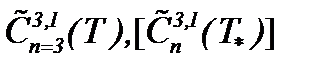 , во-вторых, – условно-гладкое единственное решение в
, во-вторых, – условно-гладкое единственное решение в 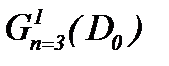 или
или 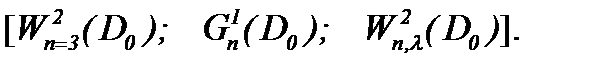
Литература
[1] Navier-Stokes Existence and Smoothness Problem. The Millennium Problems, stated in 2000 by Clay Mathematics Institute.
[2] Beale, J.T., Kato, T., Majda, A. (1984), Remarks on the breakdown of smooth solutions for the 3-D Euler equations, Comm. Math. Phys. 94 (1), pp. 61-66.
[3] Birkhoff, G. (1983), Numerical fluid dynamics. SIAM Rev., Vol. 25, No 1, pp. 1-34.
[4] Cantwell, B.J. (1981), Organized motion in turbulent flow. Ann. Rev. Fluid Mech. Vol. 13, pp. 457-515.
[5] Grujic, Z., Guberovic, R. (2010), A regularity criterion for the 3D NSE in a local version of the space of functions of bounded mean oscillations, Ann. Inst. Henri Poincare, Anal. Non Lineaire 27, pp. 773-778.
[6] Ладыженская, O.A. (1970), Математические вопросы динамики вязкой несжимаемой жидкости. Москва: Наука, 288 с.
[7] Omurov, T.D. (2013), Nonstationary Navier-Stokes Problem for Incompressible Fluid with Viscosity. American J. Math.&Statistics, Vol. 3, No 6, pp. 349-356.
(http://article.sapub.org/10.5923.j.ajms.20130306.08.html)
[8] Omurov, T.D. (2014), The Methods of a Problem Decision Navier-Stokes for the Incompressible Fluid with Viscosity. American J. of Fluid Dynamics, Vol. 4, No 1, pp. 16-48
(http://article.sapub.org/10.5923.j.ajfd.20140401.03.html )
[9] Omurov, T.D. (2013), Navier-Stokes problem for Incompressible fluid with viscosity. Varia Informatica, 2013, Ed. M.Milosz, PIPS Polish Lublin, pp. 137-158.
[10] Omurov, T.D. (2010), Нестационарная задача Навье-Стокса для несжимаемой жидкости. Бишкек: КНУ Ж. Баласагуна, 86 с. (Кыргызпатент: авторское свидетельство №1543 от 30.07.2010 г.)
[11] Prantdl, L. (1961), Gesammelte Abhandlungen zur angewandten Mechanik, Hudro- und Aerodynamic. Springer, Berlin.
[12] Шлихтинг, Г. (1974), Теория пограничного слоя. Москва: Наука, 712 с.
[13] Соболев, С.Л. (1966), Уравнения математической физики. Москва: Наука, 443 с.
[14] Friedman, A. (1958), Boundary estimates for second order parabolic equations and their application. J. of Math.and Mech., Vol. 7, No 5, pp.771-791.
[15] Hörmander, L. (1983), The Analysis of Linear Partial Differential Operators II: Differential Operators with Constant Coefficients. Springer-Verlag, Berlin Heidelberg, NY, Tokyo, 1983.





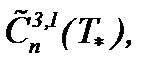 когда
когда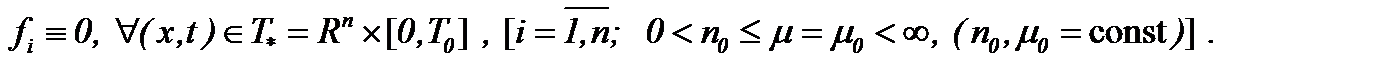 (7.21)
(7.21)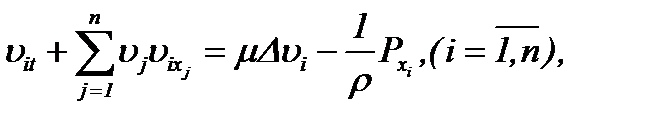 (7.22)
(7.22)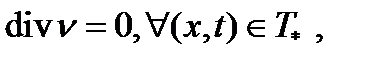 (7.23)
(7.23)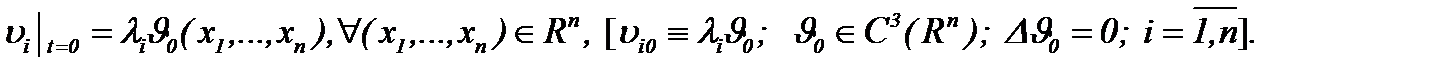 (7.24)
(7.24) .
.  , которые удовлетворяют условиям
, которые удовлетворяют условиям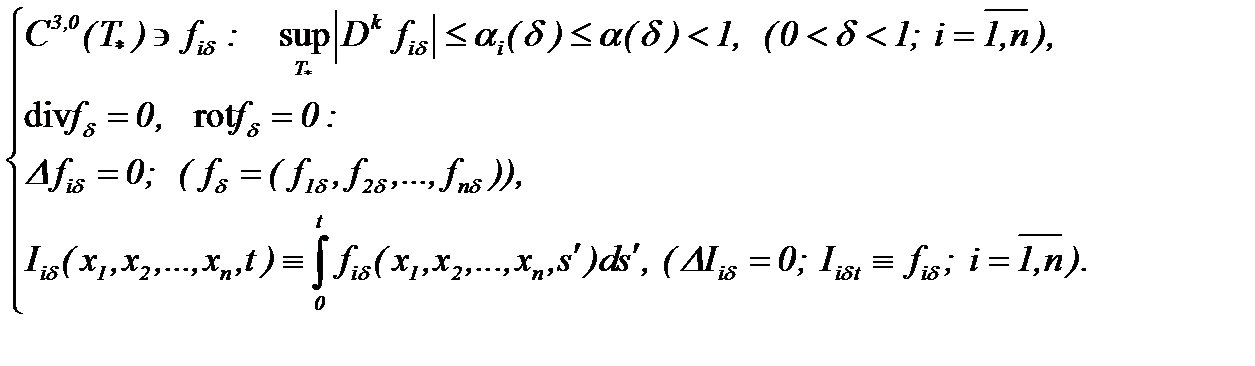 (7.25)
(7.25)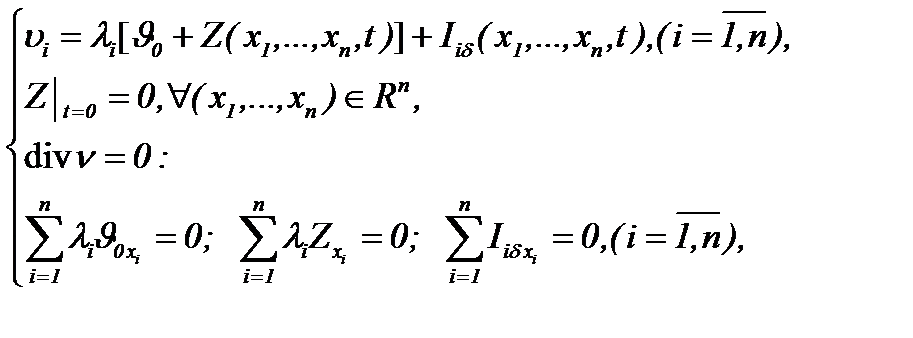 (7.26)
(7.26) 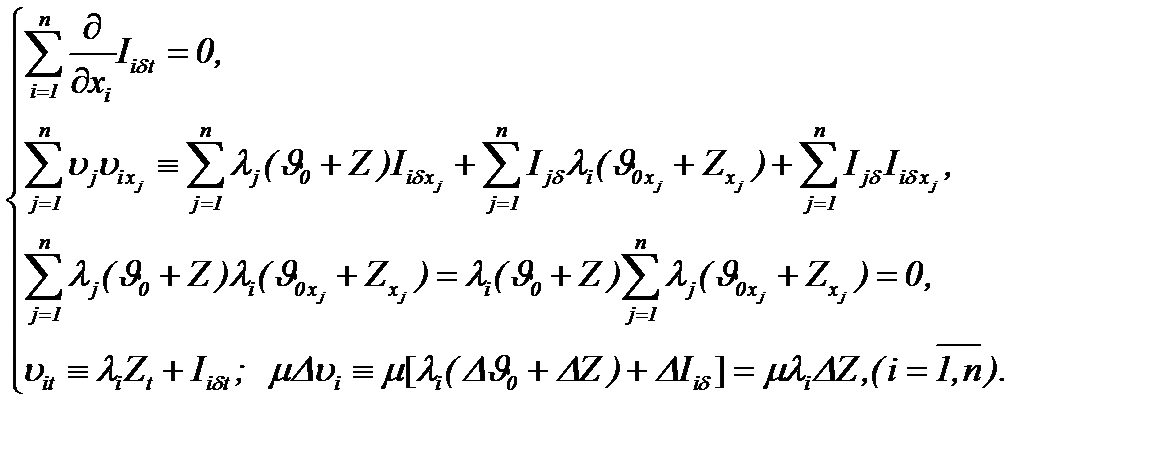 (7.27)
(7.27) 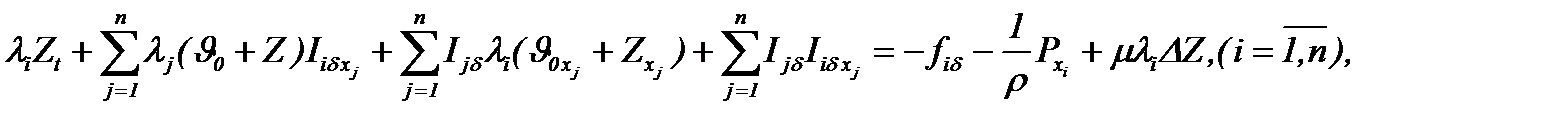 (7.28)
(7.28)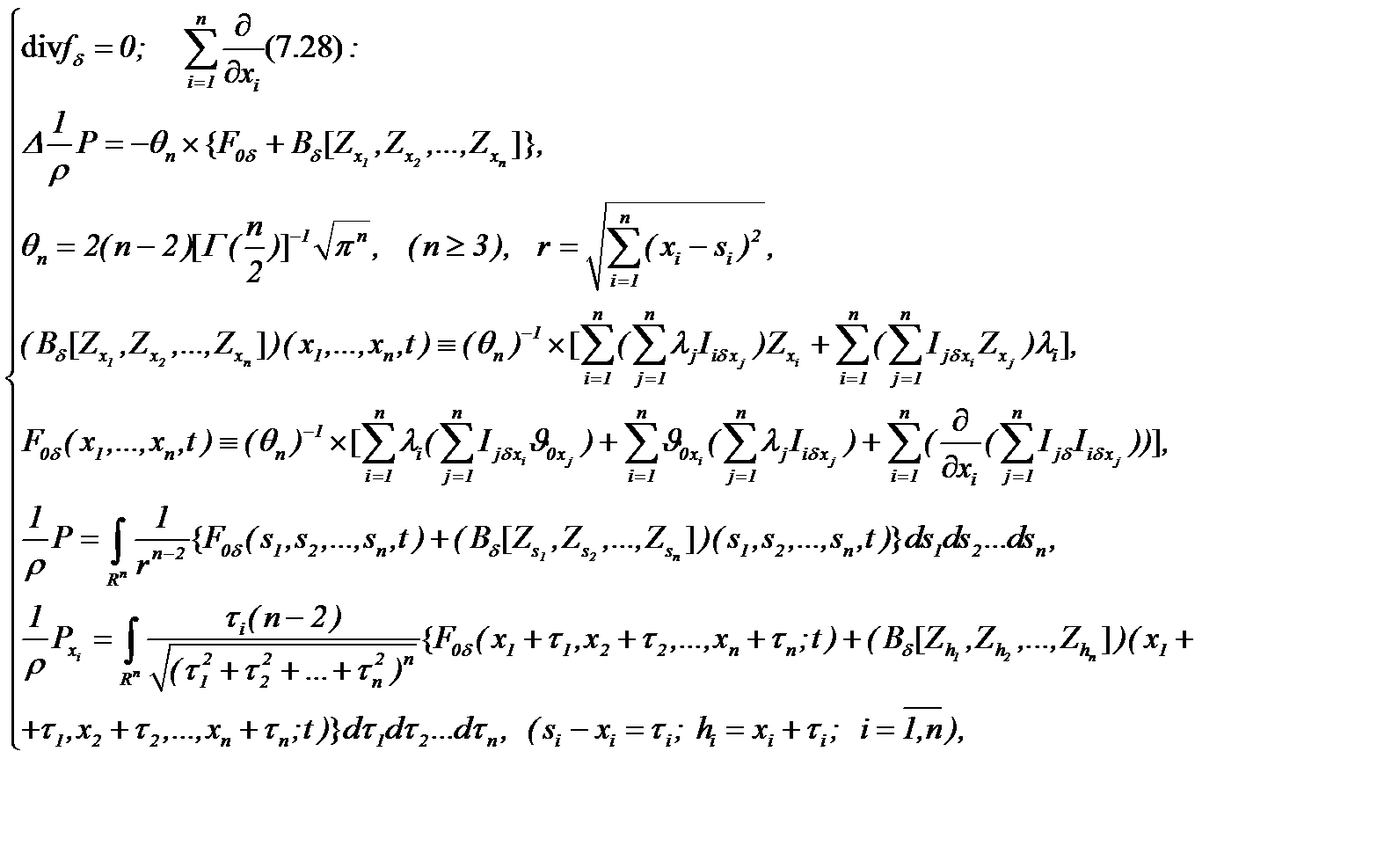 (7.29)
(7.29)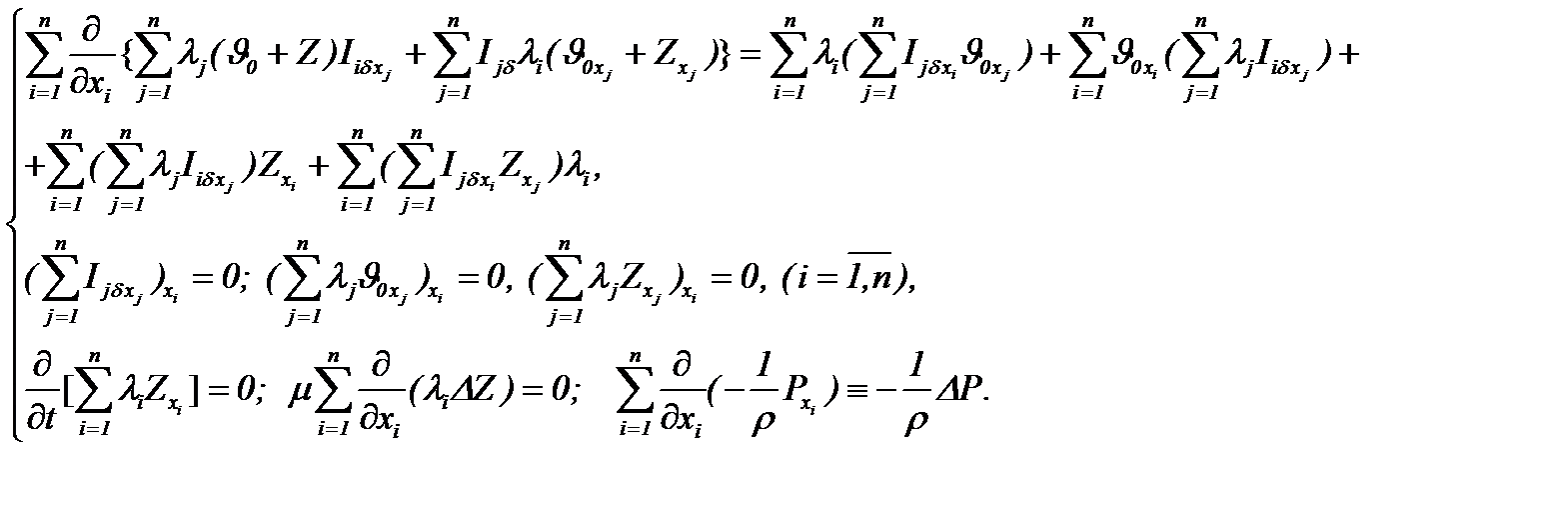
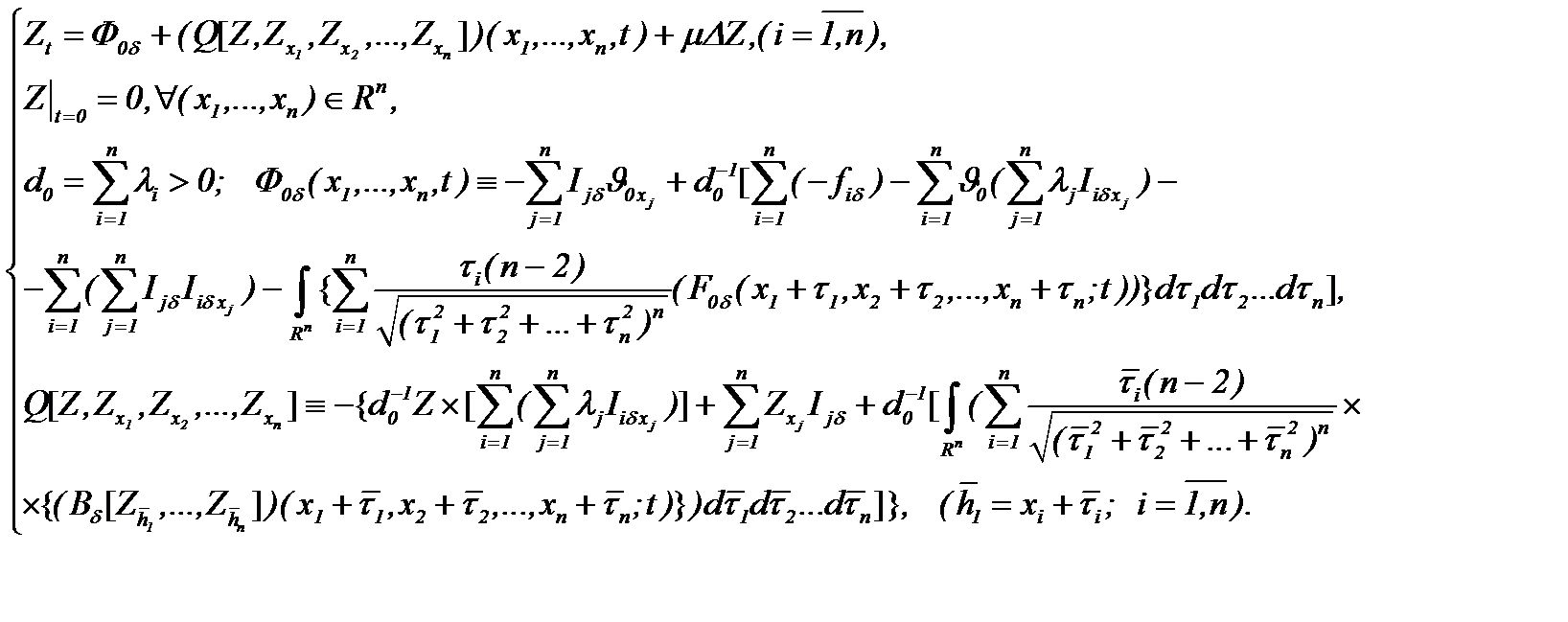 (7.30)
(7.30)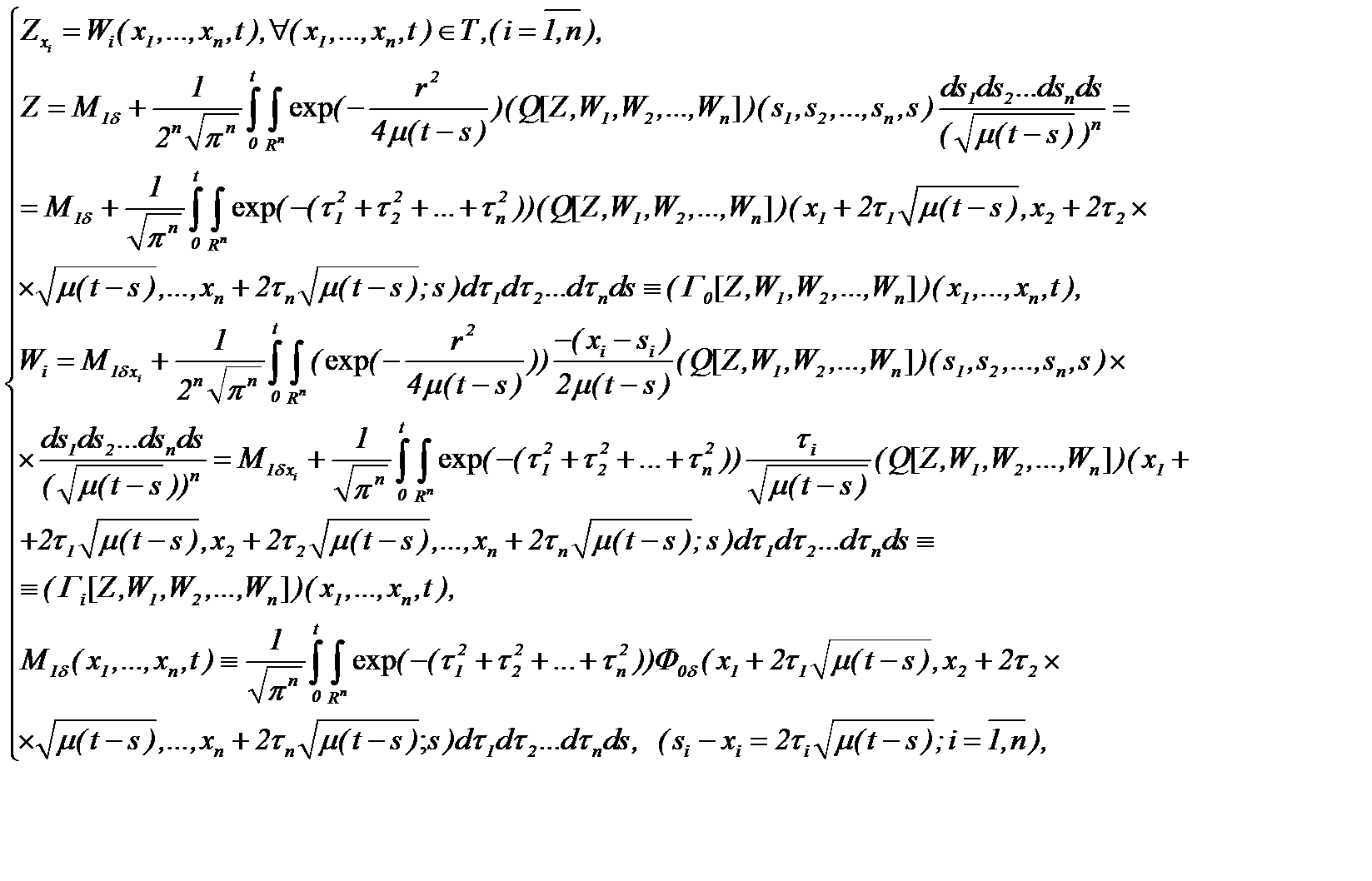 (7.31)
(7.31) » интегральных уравнений с «
» интегральных уравнений с « 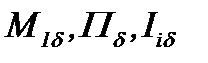 имеет место:
имеет место: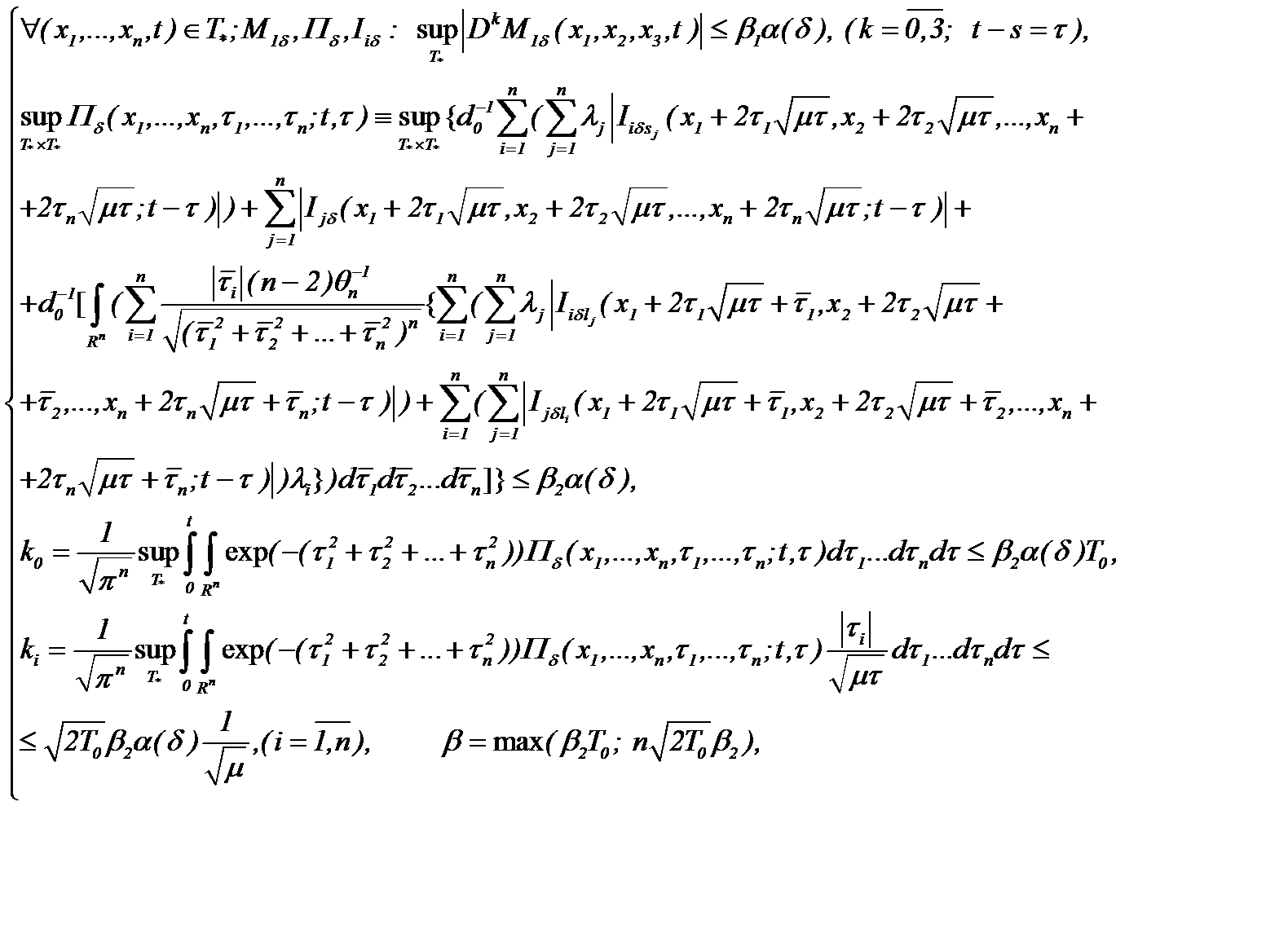 (7.32)
(7.32) допускают сжатие отображений
допускают сжатие отображений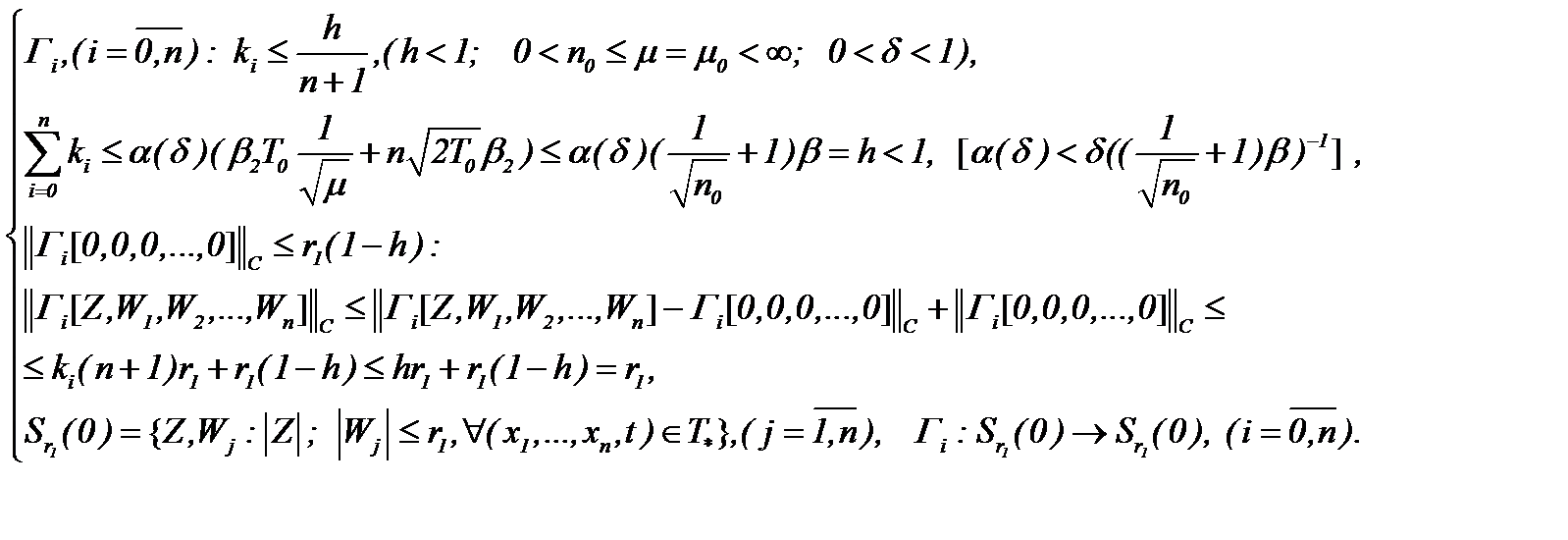 (7.33)
(7.33) (7.34)
(7.34) , которые являются сходящимися и фундаментальными в
, которые являются сходящимися и фундаментальными в  так как
так как
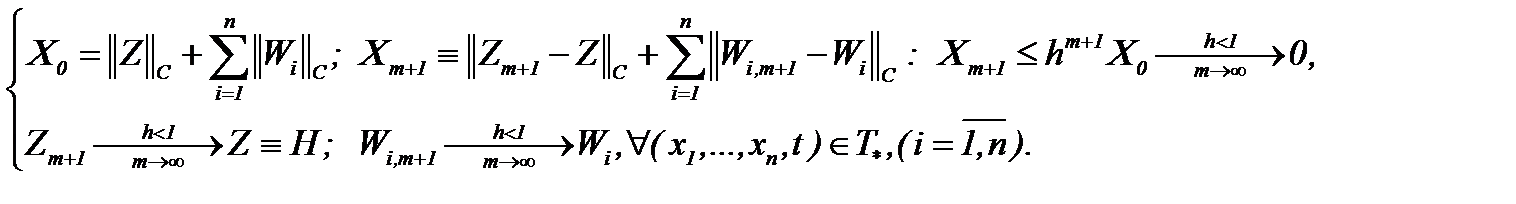 (7.35)
(7.35)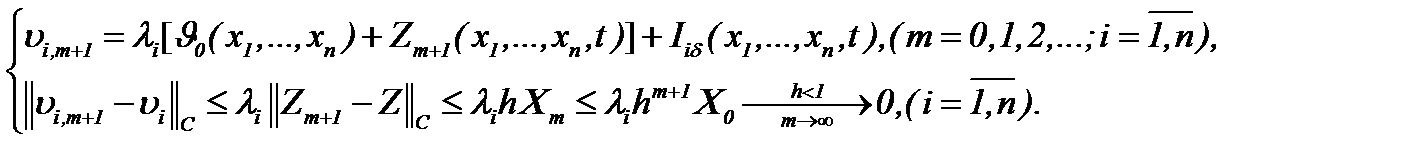 (7.36)
(7.36)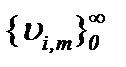 стремятся к пределу
стремятся к пределу 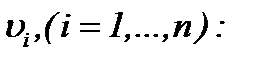
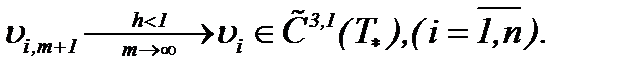 (7.37)
(7.37)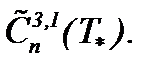
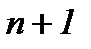 » интегральных уравнений с «
» интегральных уравнений с « 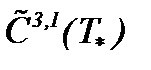 , то есть на основе (7.35) существует гладкая и единственная функция
, то есть на основе (7.35) существует гладкая и единственная функция 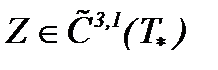 . Поэтому с учетом (7.26) при условиях (7.23), (7.24), (7.25), (7.32), (7.33) и (7.37) получим
. Поэтому с учетом (7.26) при условиях (7.23), (7.24), (7.25), (7.32), (7.33) и (7.37) получим 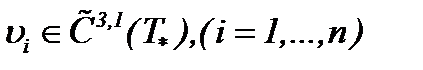 .
. 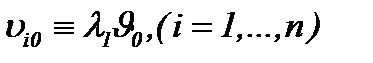 или
или 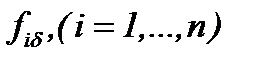 незначительно влияют на решение (7.26), то есть решение непрерывно зависит от этих данных. Поэтому, вопрос о корректности задачи (7.22) – (7.24) разрешается на основе результатов теоремы 9 в
незначительно влияют на решение (7.26), то есть решение непрерывно зависит от этих данных. Поэтому, вопрос о корректности задачи (7.22) – (7.24) разрешается на основе результатов теоремы 9 в 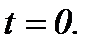 Поэтому преобразованные задачи сохраняют математические и физические закономерности постановки исходной задачи и значения переменных, отвечающих требованиям Математического Института Клея.
Поэтому преобразованные задачи сохраняют математические и физические закономерности постановки исходной задачи и значения переменных, отвечающих требованиям Математического Института Клея. 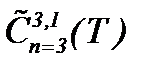 , где, относительно параметра вязкости, условие регулярности интегралов выражается в терминах времени интегрируемости. Когда аналитическое решение 3D уравнений Навье-Стокса удовлетворяет условия критерия Билла-Като-Мажда, то автоматически доказываются условия критерия и для 3D уравнений
, где, относительно параметра вязкости, условие регулярности интегралов выражается в терминах времени интегрируемости. Когда аналитическое решение 3D уравнений Навье-Стокса удовлетворяет условия критерия Билла-Като-Мажда, то автоматически доказываются условия критерия и для 3D уравнений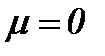 отвечает уравнению идеальной жидкости.
отвечает уравнению идеальной жидкости.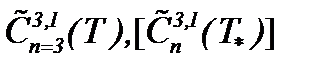 , во-вторых, – условно-гладкое единственное решение в
, во-вторых, – условно-гладкое единственное решение в 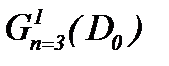 или
или