

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...
Топ:
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Интересное:
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
I . Несжимаемые потоки без трения. Для несжимаемых течений без трения [2, 6, 12], когда 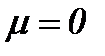 , уравнения Навье-Стокса упрощаются, поскольку нет члена
, уравнения Навье-Стокса упрощаются, поскольку нет члена 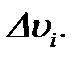 Поэтому задача (1.1) – (1.3) приводится к виду
Поэтому задача (1.1) – (1.3) приводится к виду
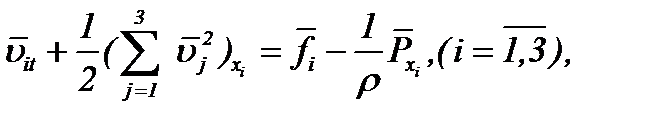 (2.25)
(2.25)
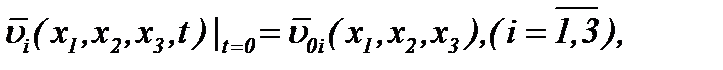 (2.26)
(2.26)
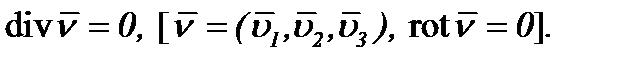 (2.27)
(2.27)
Система (2.25) с условиями (2.26), (2.27) имеет строгое решение с сохранением всех конвективных членов при выполнении условия Стокса [12]. Так как для несжимаемых течений без трения вектор скорости представляется, как градиент потенциала 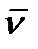 , но этот потенциал удовлетворяет уравнению Лапласа, то для потенциальных течений зависящий от вязкости член уравнения (1.1) тождественно исчезает. При этом система (2.25) имеет гладкое единственное решение в
, но этот потенциал удовлетворяет уравнению Лапласа, то для потенциальных течений зависящий от вязкости член уравнения (1.1) тождественно исчезает. При этом система (2.25) имеет гладкое единственное решение в 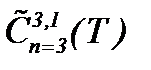 (см. также [9], с.147-151)
(см. также [9], с.147-151)
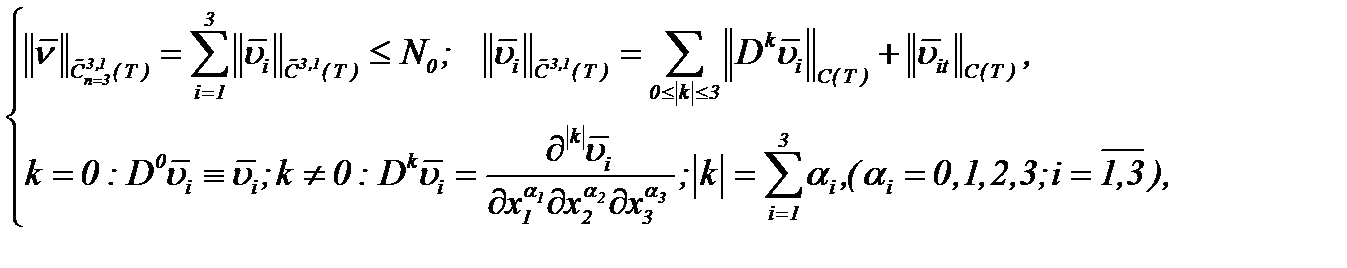 (2.28)
(2.28)
где рассматриваемые функции являются гармоническими функциями.
Указанный метод теоремы 2* может быть использован, в частности, для решения задачи (2.25) – (2.27) в качестве тестового примера. Действительно, на основе АПС из системы (2.25) следует
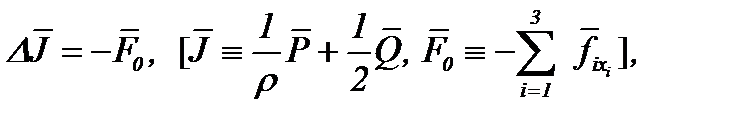 (2.29)
(2.29)
причем
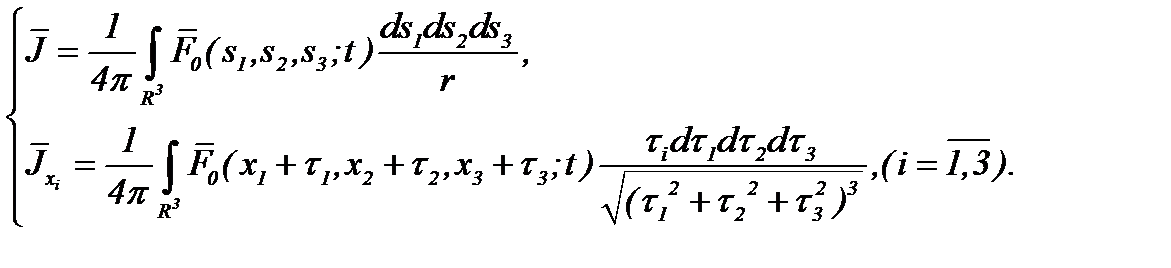 (2.30)
(2.30)
Так как 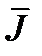 – решение уравнения (2.29), то с учетом
– решение уравнения (2.29), то с учетом
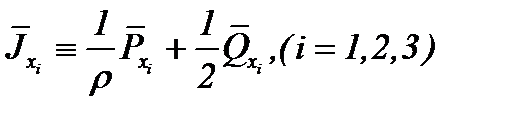
из (2.25) получим
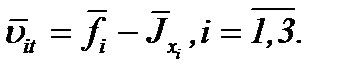 (2.31)
(2.31)
Отсюда, на основании (2.26) следует
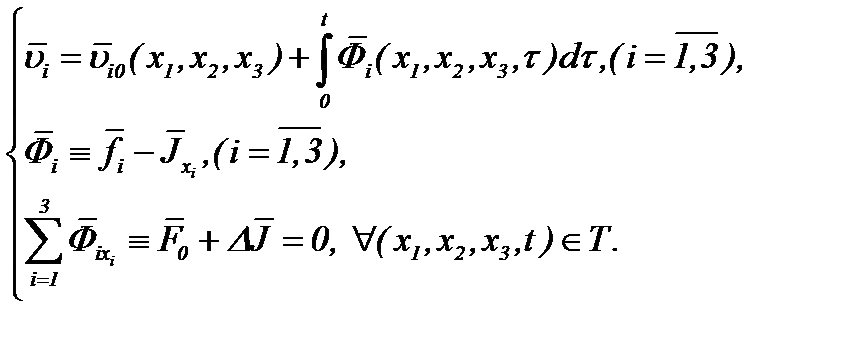 (2.32)
(2.32)
Тогда из (2.29) и (2.30) имеем
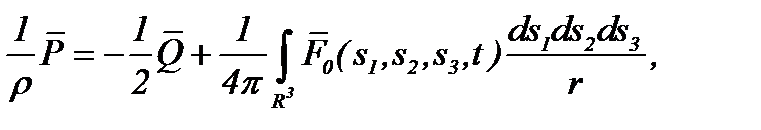 (2.33)
(2.33)
т.е. получаем уравнение типа Бернулли, которое аналогично (2.23)*.
Поскольку из полученных результатов система (2.32) удовлетворяет условию (2.27), то
найденные решения 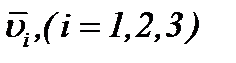 удовлетворяют уравнению Лапласа, а, значит, представимы гармоническими функциями, что и требовалось показать.
удовлетворяют уравнению Лапласа, а, значит, представимы гармоническими функциями, что и требовалось показать.
II . Известно, что предельный переход к очень малой вязкости должен быть выполнен не в уравнениях Навье-Стокса, а в решении этих уравнений путем приближения коэффициента вязкости к нулю [12]. В нашем случае решение системы (1.1) представляется в форме (2.19) с соблюдением условий теоремы 2*, поэтому для оценки близости решений (2.19) и (2.32) в смысле 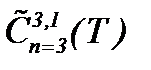 , когда
, когда 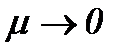 , требуется выполнить условия:
, требуется выполнить условия:
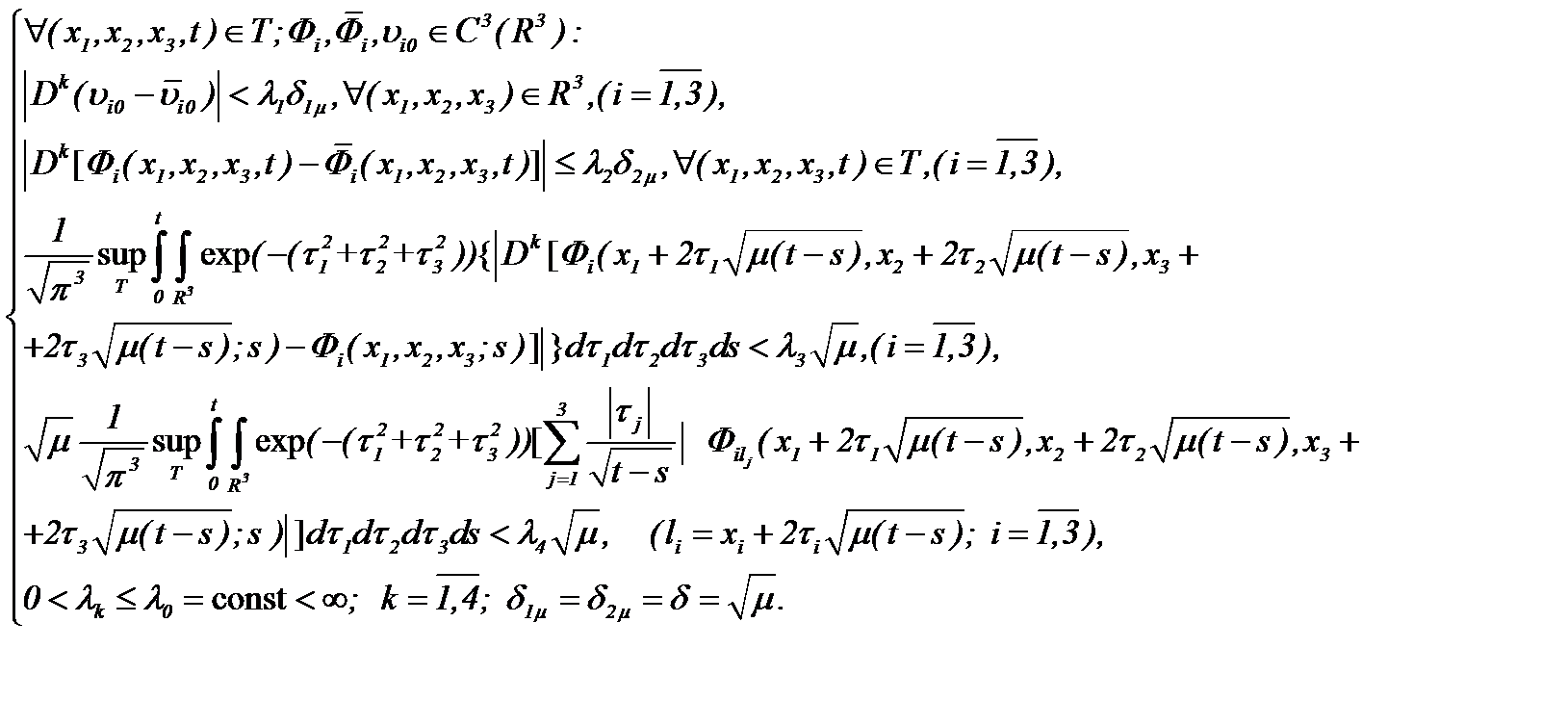 (2.34)
(2.34)
Лемма 1. Если выполнены условия теоремы 2* и (2.34), то допустимая погрешность оценки между решениями систем (2.19), (2.32) будет порядка 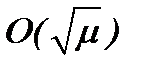 в
в 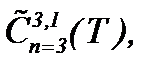 когда
когда 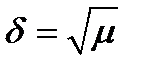 .
.
Доказательство. Чтобы доказать близость решений (2.19) и (2.32) в 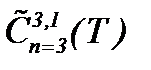 , сначала докажем близость решений в
, сначала докажем близость решений в 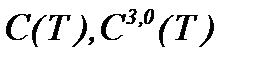 . Тогда, очевидно, что оценка относительно
. Тогда, очевидно, что оценка относительно 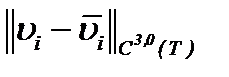 будет иметь порядок
будет иметь порядок 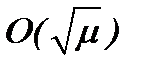 .
.
Действительно, оценивая разности системы (2.19) и (2.32), получим
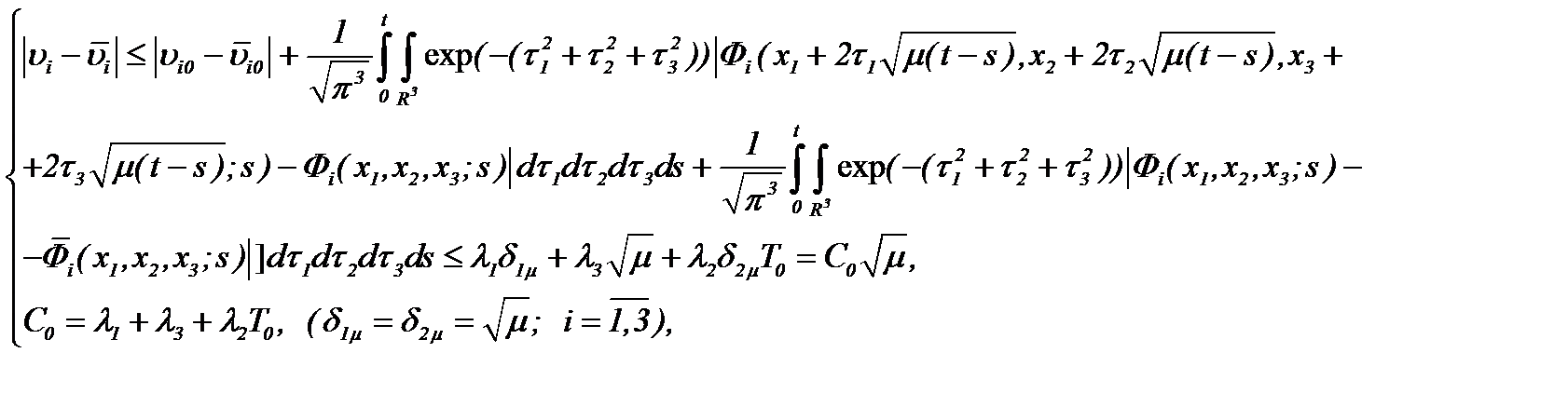
или, оценивая в смысле нормы 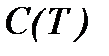 , имеем
, имеем
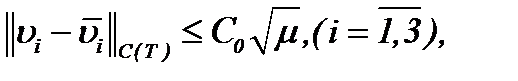
где (см. (2.32)):
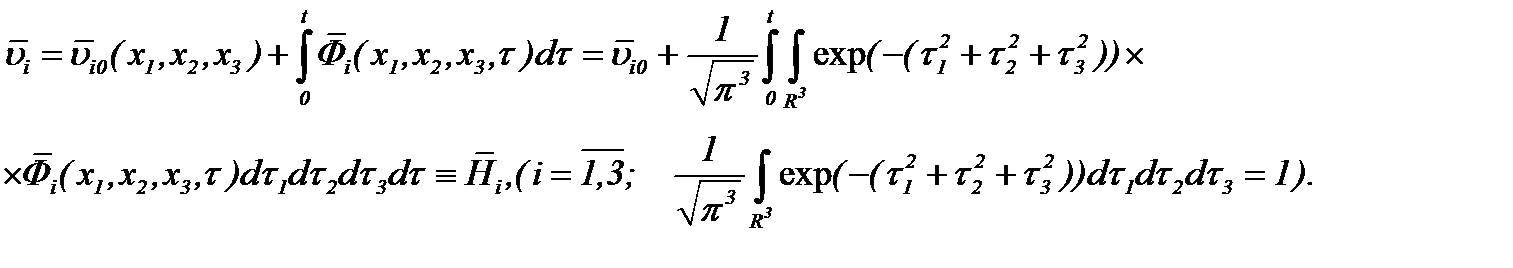 (2.32)*
(2.32)*
Точно так же получим оценки, касающиеся выражения с частными производными функций 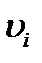 и
и 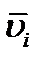 до третьего порядка, включительно, а именно
до третьего порядка, включительно, а именно
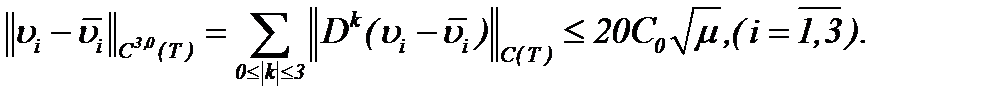
Теперь, так как 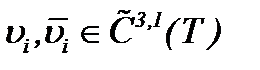 , то, оценивая (2.19) и (2.32)* в смысле нормы
, то, оценивая (2.19) и (2.32)* в смысле нормы 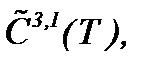 получим
получим
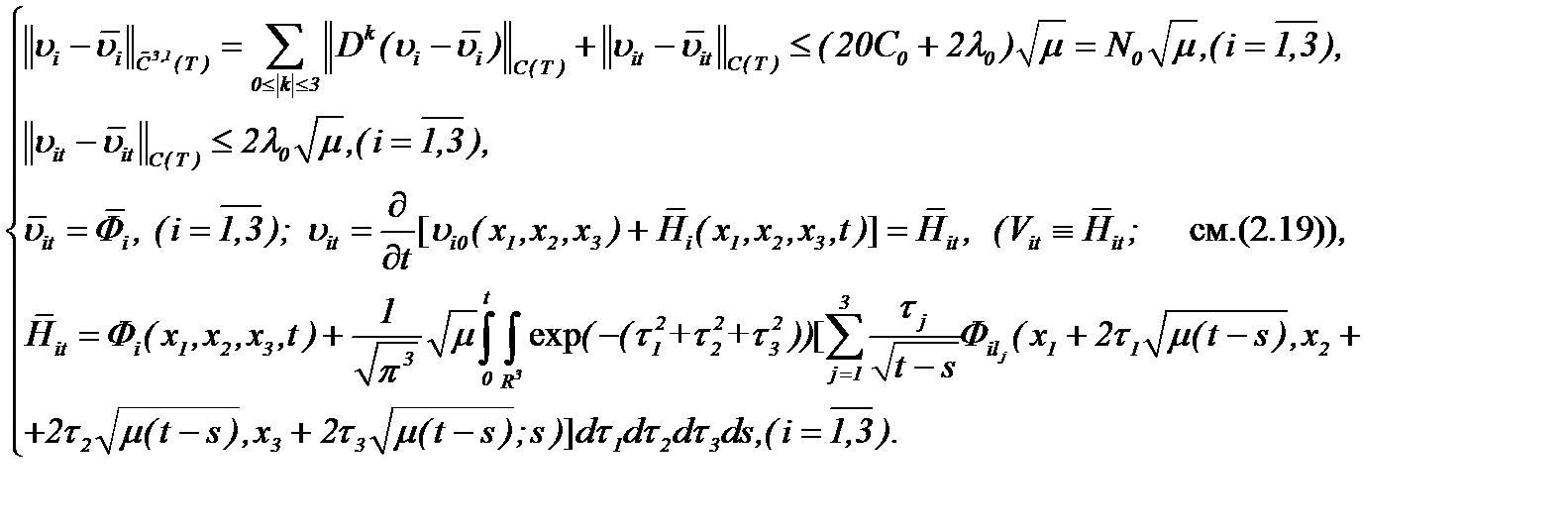 (2.35)
(2.35)
Тогда с учетом (2.35) и 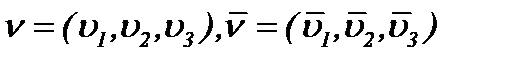 , имеем
, имеем
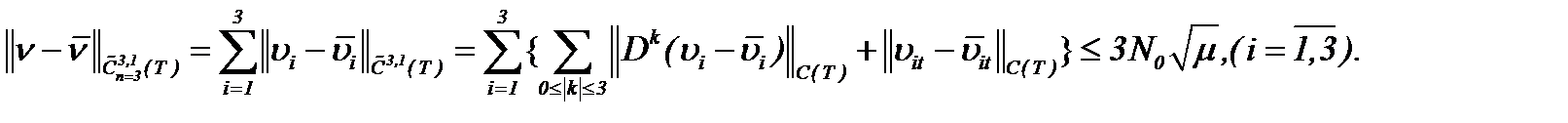 (2.36)
(2.36)
А это значит, что выполнение равенства 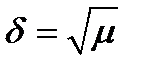 ведет к тому, что допустимая погрешность оценки будет порядка
ведет к тому, что допустимая погрешность оценки будет порядка 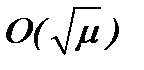 в
в 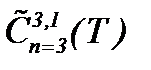 . Лемма 1 доказана. ■
. Лемма 1 доказана. ■
Замечание *. Так как 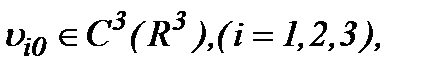 то чтобы оценить близость решений (2.10), (2.32) в смысле
то чтобы оценить близость решений (2.10), (2.32) в смысле 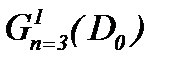 требуем условия теоремы 2 и (2.34), когда
требуем условия теоремы 2 и (2.34), когда 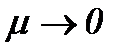 . При этом имеем
. При этом имеем
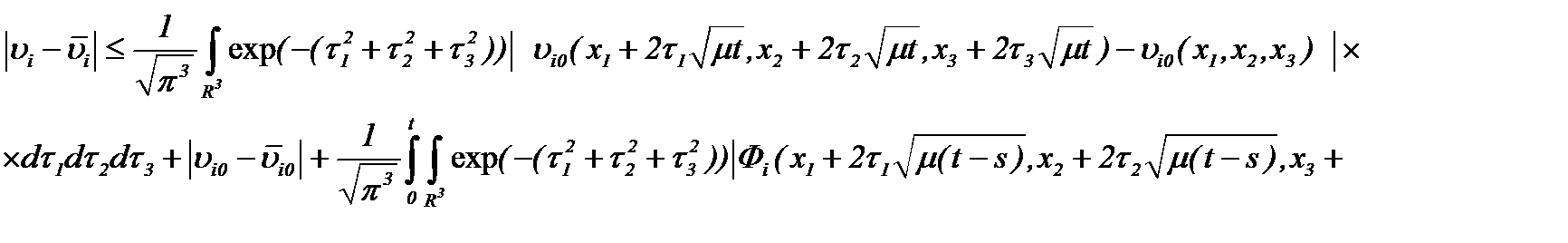
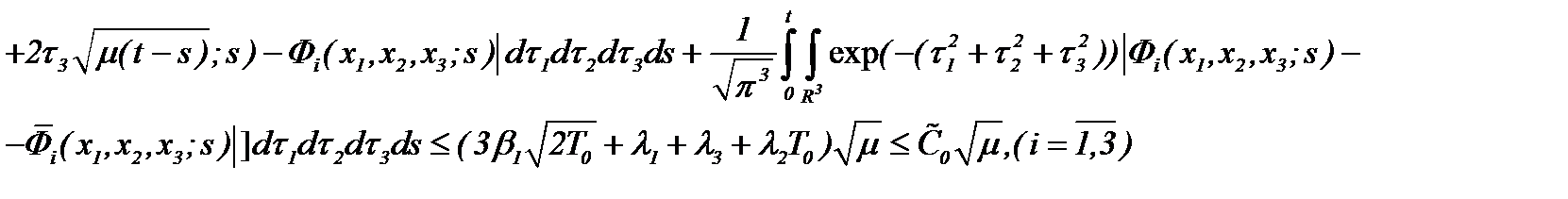
или
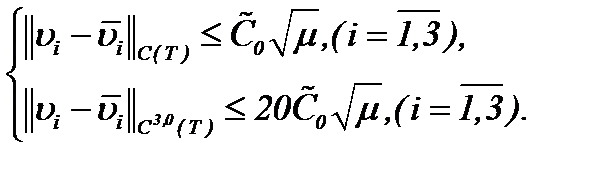 (2.37)
(2.37)
Точно так же мы получим оценку и относительно 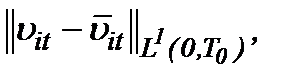 т.е.
т.е.
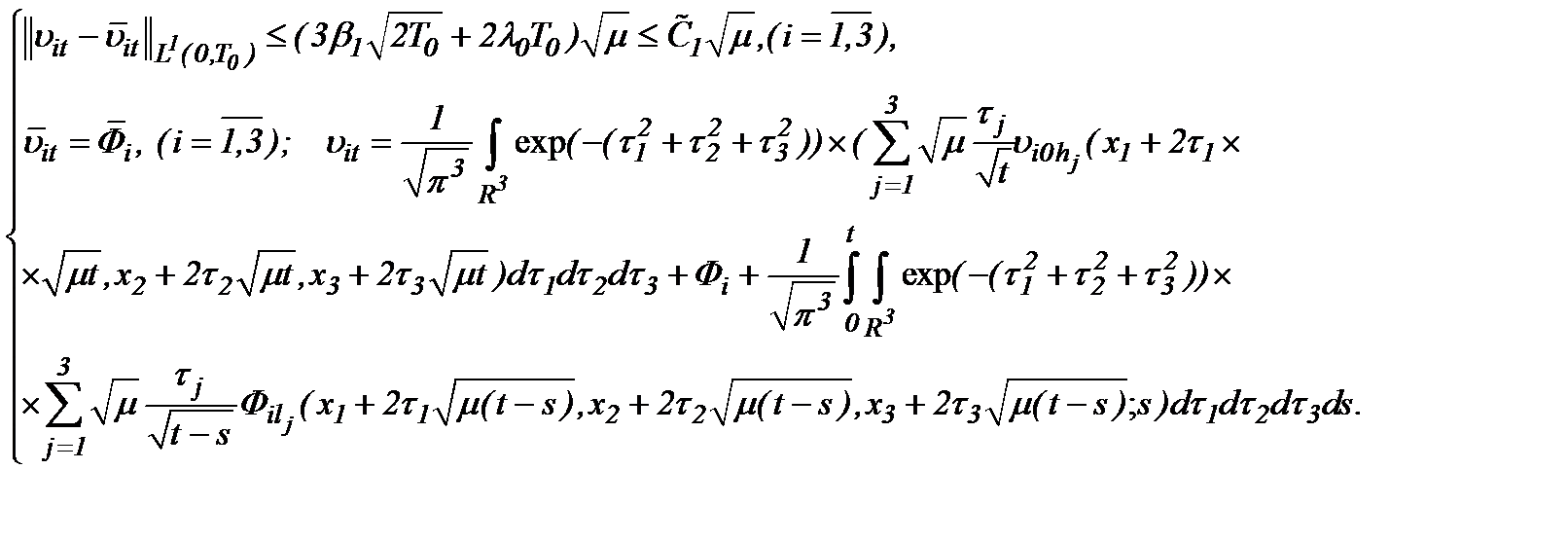 (2.38)
(2.38)
Тогда принимая во внимание (2.37), (2.38) и оценивая  в
в  , получим
, получим
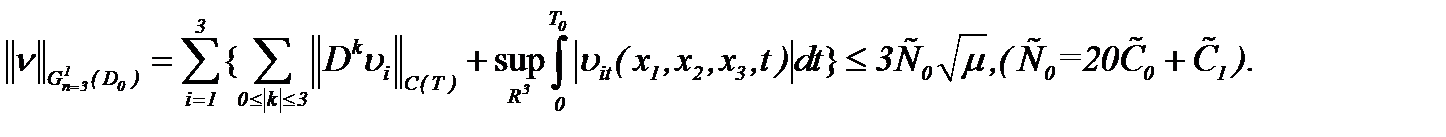 (2.39)
(2.39)
Утверждение 2. В условиях теоремы 2 и (2.34), (2.39) допустимая погрешность оценки между решениями систем (2.10), (2.32) в 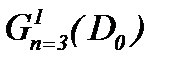 будет порядка
будет порядка 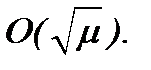
3. Жидкость Средней Вязкости с Условием ( A 2 )
В задачах Навье-Стокса с большими значениями вязкости, т.е. с небольшим числом Рейнольдса ( 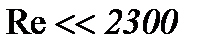 ) скорость может быть настолько мала, что во многих исследованиях пренебрегают силами инерции [12], например, в случае течений Хил-Шоу, так же как и в случае течения смазочного масла, где число Рейнольдса
) скорость может быть настолько мала, что во многих исследованиях пренебрегают силами инерции [12], например, в случае течений Хил-Шоу, так же как и в случае течения смазочного масла, где число Рейнольдса 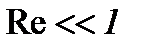 . Как только число Рейнольдса становится больше единицы, силы инерции начинают играть существенный роль. Поэтому, во многих задачах ползущего течения существует принципиальная возможность распространения решений на область более высоких чисел Рейнольдса методом последовательных приближений. Для этой цели инерционные члены вычисляются из первого приближения и затем вводятся в уравнения в качестве внешних сил. Но такой путь совершенно не пригоден для теоретического проникновения в область средних по величине чисел Рейнольдса, в которой силы трения и силы инерции имеют величины одинакового порядка во всем течений. Теоретически, уравнения Навье-Стокса такого вида, если не считать работы [8, 9], до сих пор не исследованы в полном объеме. Поэтому, разработка методов интегрирования уравнений Навье-Стокса, является сутью этого пункта, когда (А2).
. Как только число Рейнольдса становится больше единицы, силы инерции начинают играть существенный роль. Поэтому, во многих задачах ползущего течения существует принципиальная возможность распространения решений на область более высоких чисел Рейнольдса методом последовательных приближений. Для этой цели инерционные члены вычисляются из первого приближения и затем вводятся в уравнения в качестве внешних сил. Но такой путь совершенно не пригоден для теоретического проникновения в область средних по величине чисел Рейнольдса, в которой силы трения и силы инерции имеют величины одинакового порядка во всем течений. Теоретически, уравнения Навье-Стокса такого вида, если не считать работы [8, 9], до сих пор не исследованы в полном объеме. Поэтому, разработка методов интегрирования уравнений Навье-Стокса, является сутью этого пункта, когда (А2).
Разработанный метод решения системы (1.1) связан с функциями 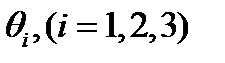 , где указанные функции преобразуют (1.1) в системы (1.4), (1.5) с условиями (а02) и
, где указанные функции преобразуют (1.1) в системы (1.4), (1.5) с условиями (а02) и
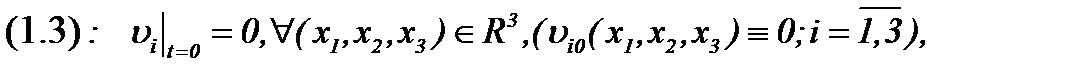 (1.3)*
(1.3)*
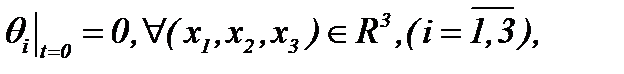 (3.1)
(3.1)
где поток считается со средним размером вязкости.
Теорема 3. Системы (1.4), (1.5) эквивалентно преобразуются к виду
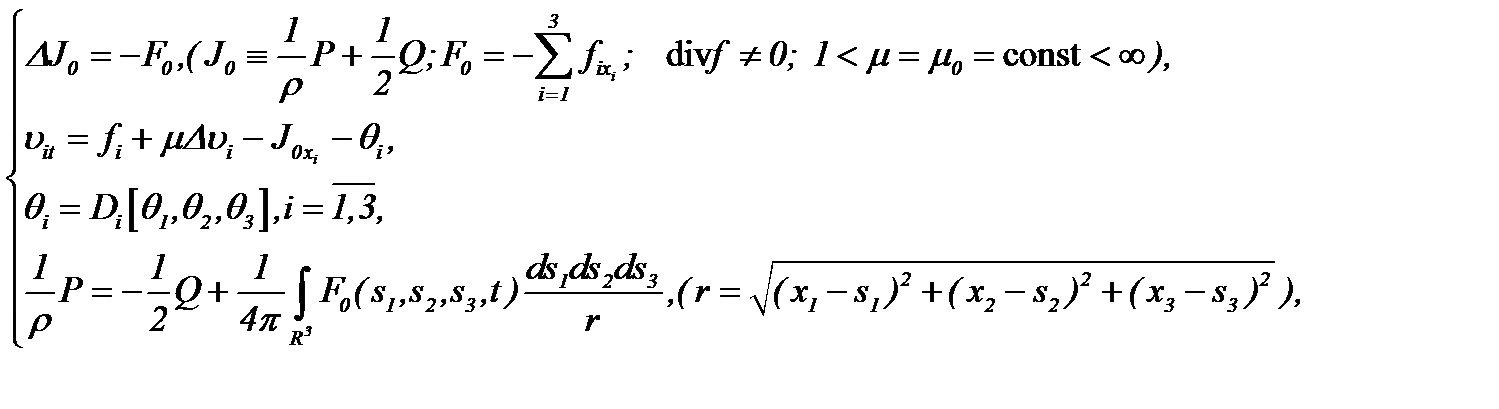 (3.2)
(3.2)
при выполнении условий (1.2), (1.3)*, (3.1) и (А2). Следовательно, нестационарная задача Навье-Стокса (1.1) – (1.3)* имеет гладкое единственное решение.
Доказательство. Действительно, из системы (1.4), учитывая условия (1.2), (1.3)*, (3.1) и применяя АПС, т.е. дифференцируя уравнения системы (1.4) соответственно по 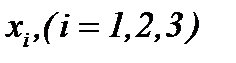 , а, затем, подводя итог, имеем уравнение
, а, затем, подводя итог, имеем уравнение
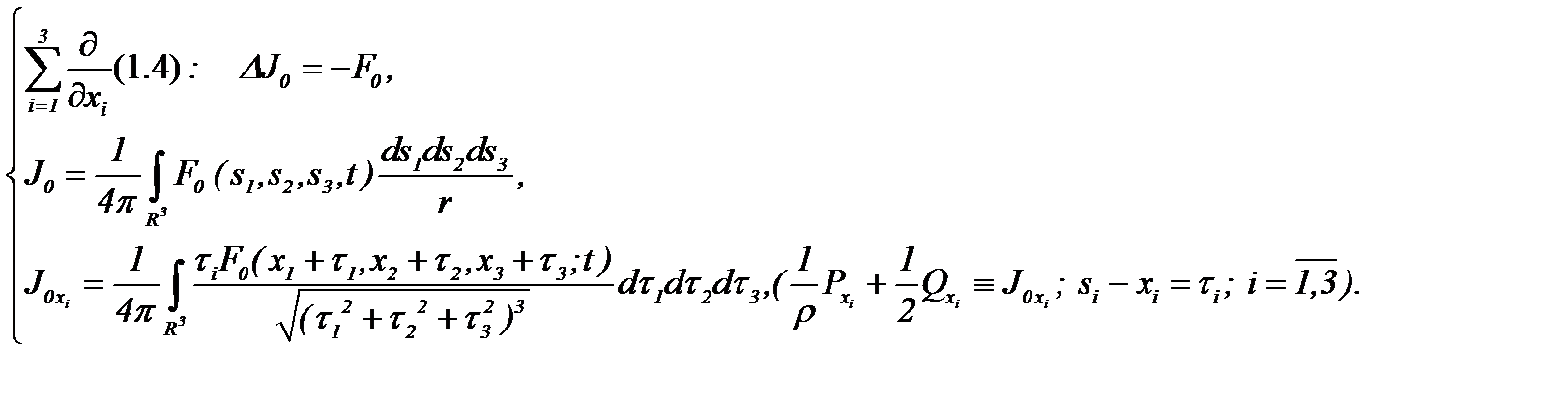 (3.3)
(3.3)
Так как 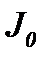 решение уравнения (3.3), то подставляя:
решение уравнения (3.3), то подставляя: 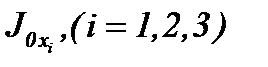 в систему (1.4) получим
в систему (1.4) получим
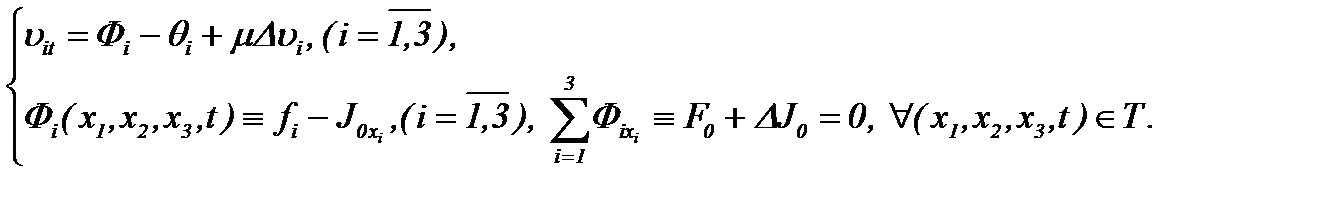 (3.4)
(3.4)
Тогда решение задачи (1.1) – (1.3)* представимо в виде
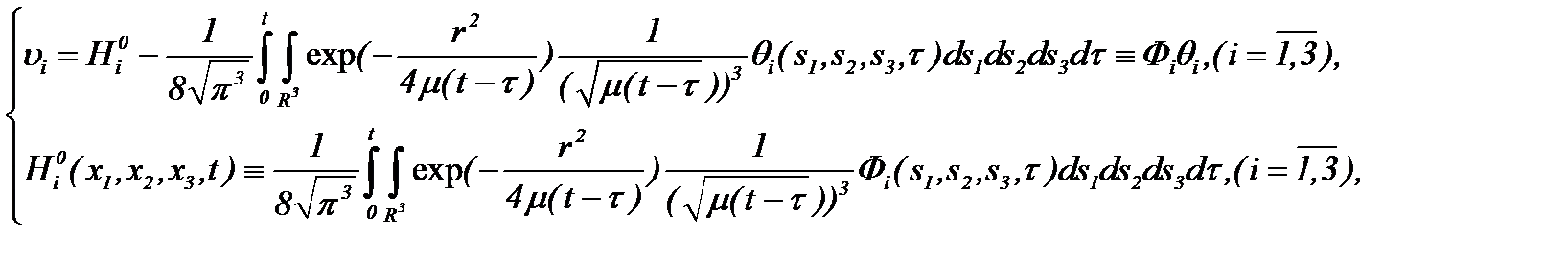 (3.5)
(3.5)
где в отношении функции 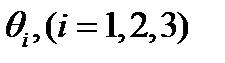 имеем
имеем
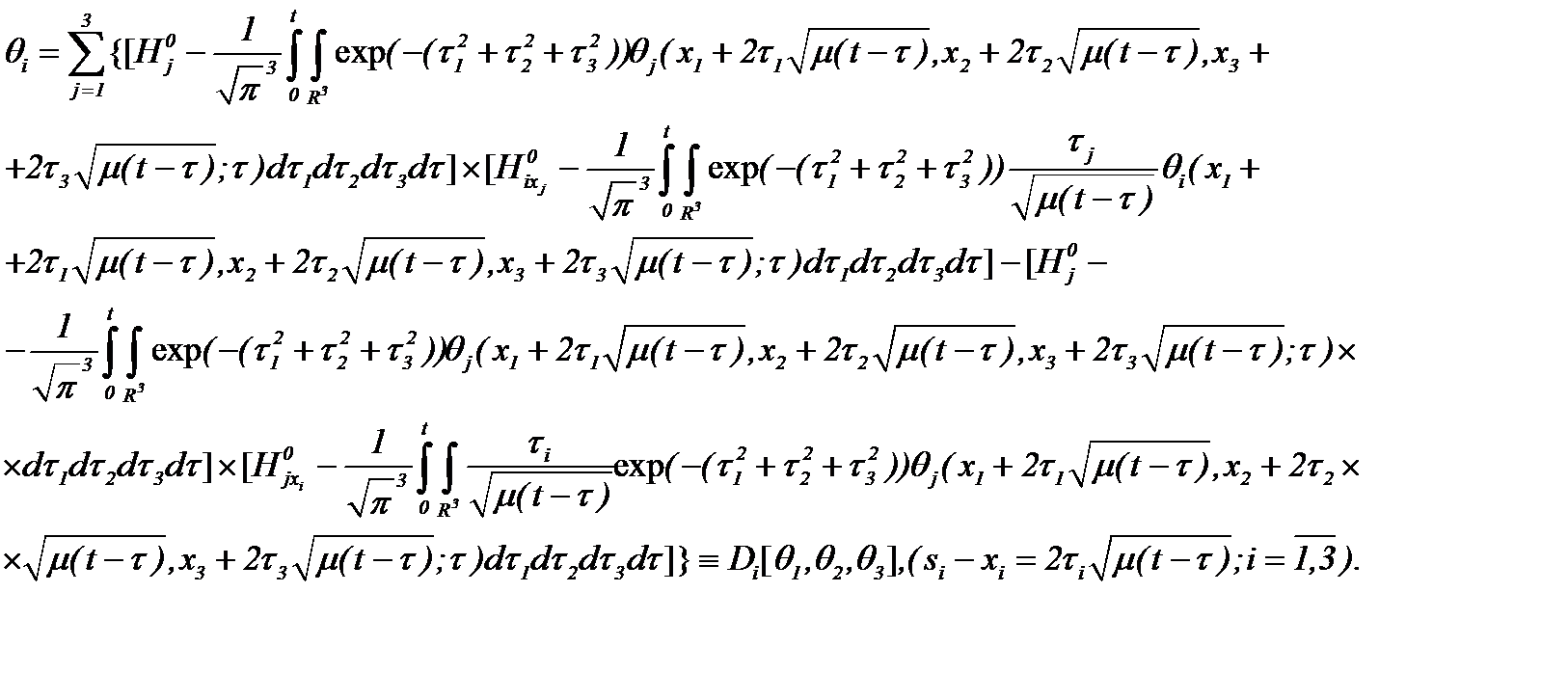 (3.6)
(3.6)
Здесь частные производные функции 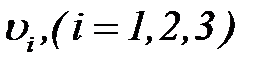 определены следующим образом
определены следующим образом
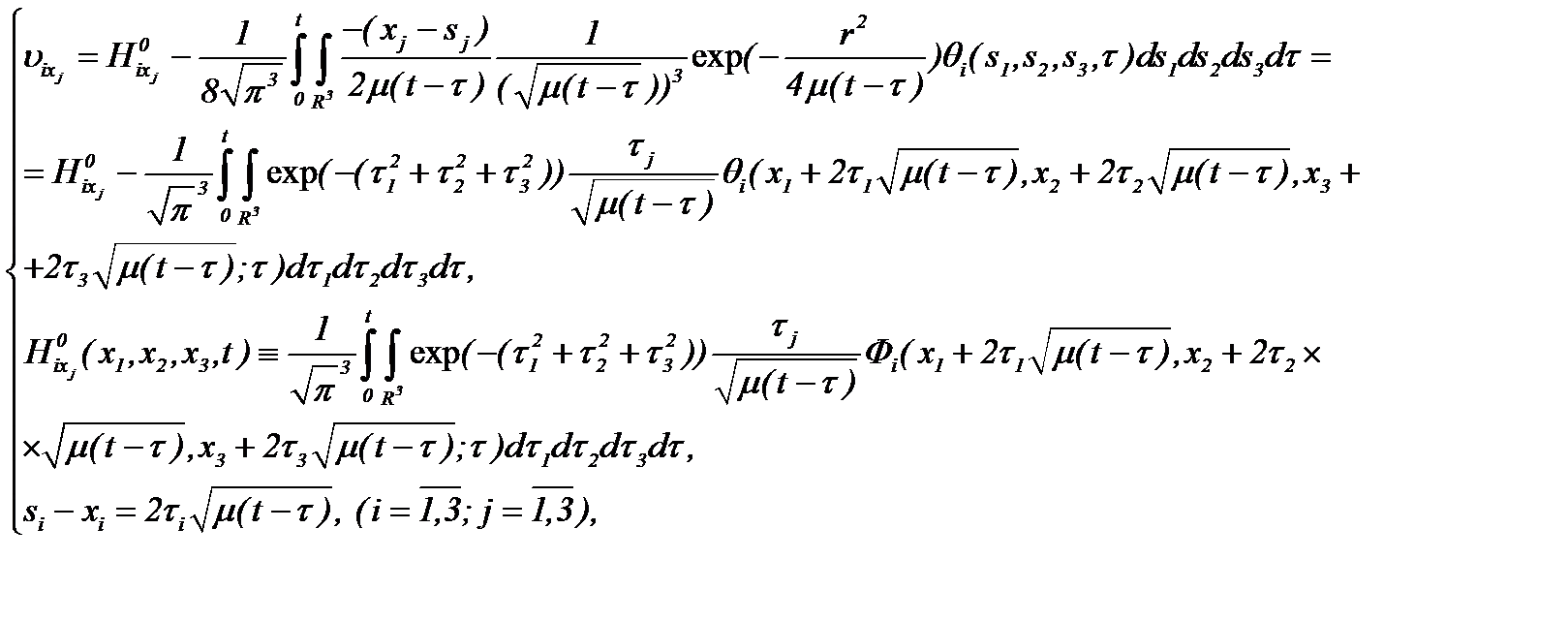 (3.7)
(3.7)
где выражение (3.6) – это система нелинейных интегральных уравнений Вольтерра-Абеля второго рода по переменной 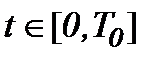 , которая состоит из трех интегральных уравнений с тремя неизвестными функциями
, которая состоит из трех интегральных уравнений с тремя неизвестными функциями 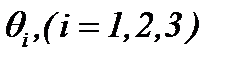 .
.
Теория указанных систем – хорошо развитая область математики [13], поэтому нет никакой необходимости изобретать различные алгоритмы для решения системы (3.6). Достаточно показать условия, которые обеспечивают принцип сжатых отображений для разрешимости этой системы, чтобы для решения можно было применить метод Пикара.
Если относительно известных данных имеет место
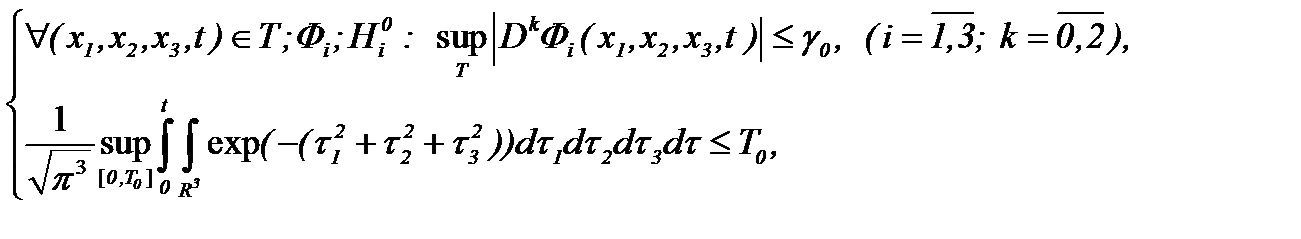
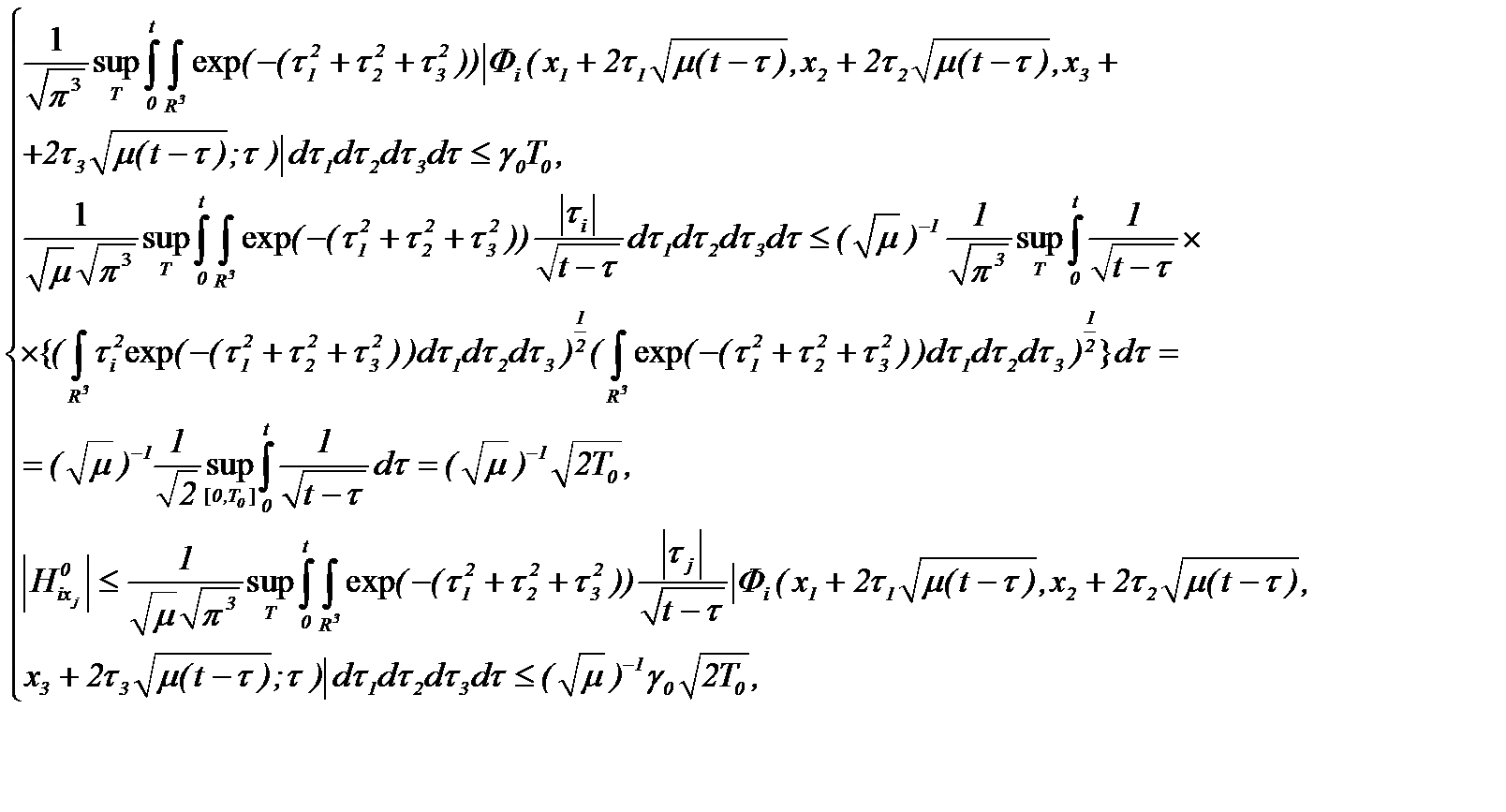 (3.8)
(3.8)
причем операторы 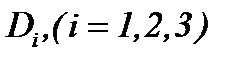 допускают условия сжатия с коэффициентами сжатия
допускают условия сжатия с коэффициентами сжатия 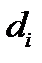
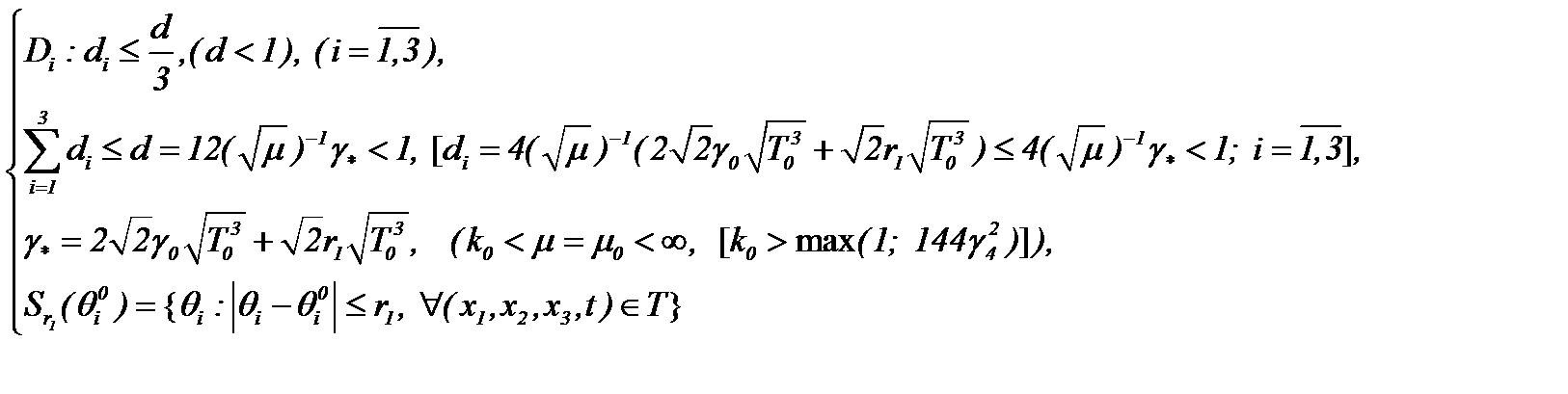 (3.9) и отображают области определения в себя
(3.9) и отображают области определения в себя
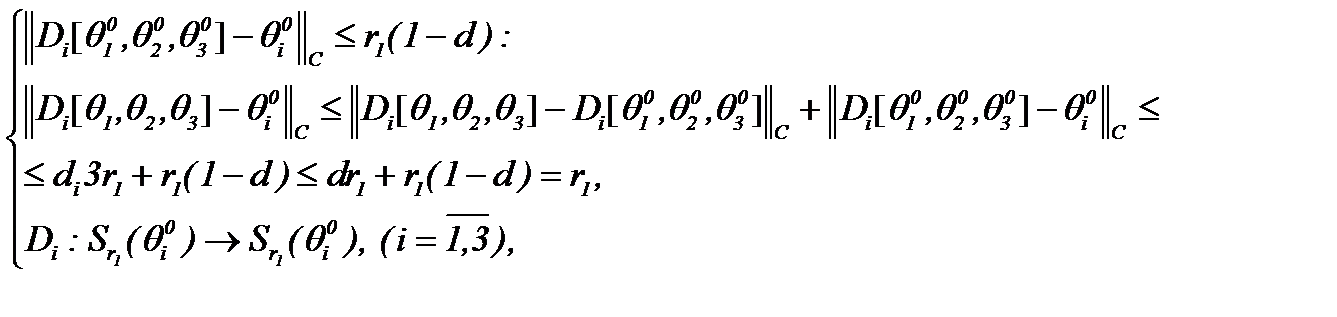 (3.10)
(3.10)
то на основании принципа сжимающих отображений система (3.6) разрешима в 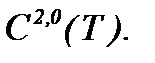 Следовательно, решение этой системы можем найти на основе метода Пикара
Следовательно, решение этой системы можем найти на основе метода Пикара
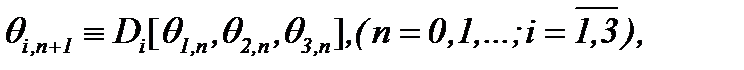 (3.11)
(3.11)
где 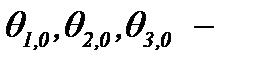 начальные приближения. Тогда, учитывая выводы метода последовательных приближений, находим, что построенные последовательности функции по правилу (3.11):
начальные приближения. Тогда, учитывая выводы метода последовательных приближений, находим, что построенные последовательности функции по правилу (3.11): 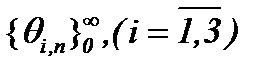 являются сходящимися и фундаментальными в
являются сходящимися и фундаментальными в 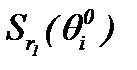 , так как
, так как
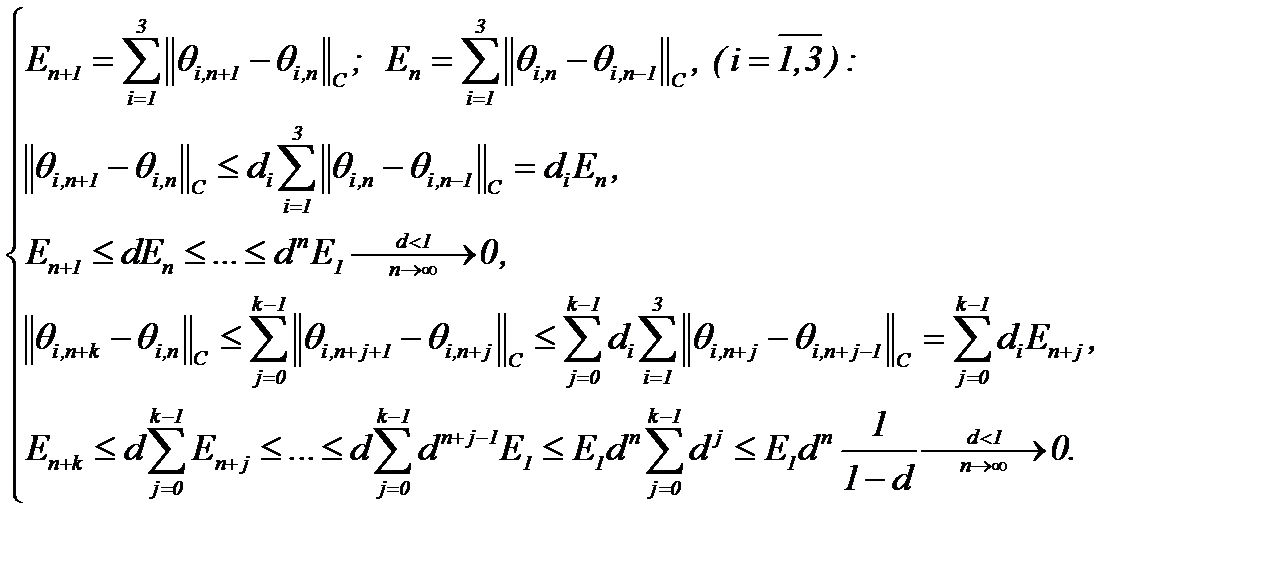
Причем, то, что элементы построенных последовательностей принадлежат 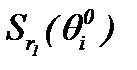 , доказывается на основе выражения (3.10). В самом деле, для
, доказывается на основе выражения (3.10). В самом деле, для 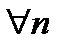 , относительно
, относительно 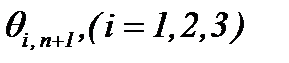 имеем
имеем
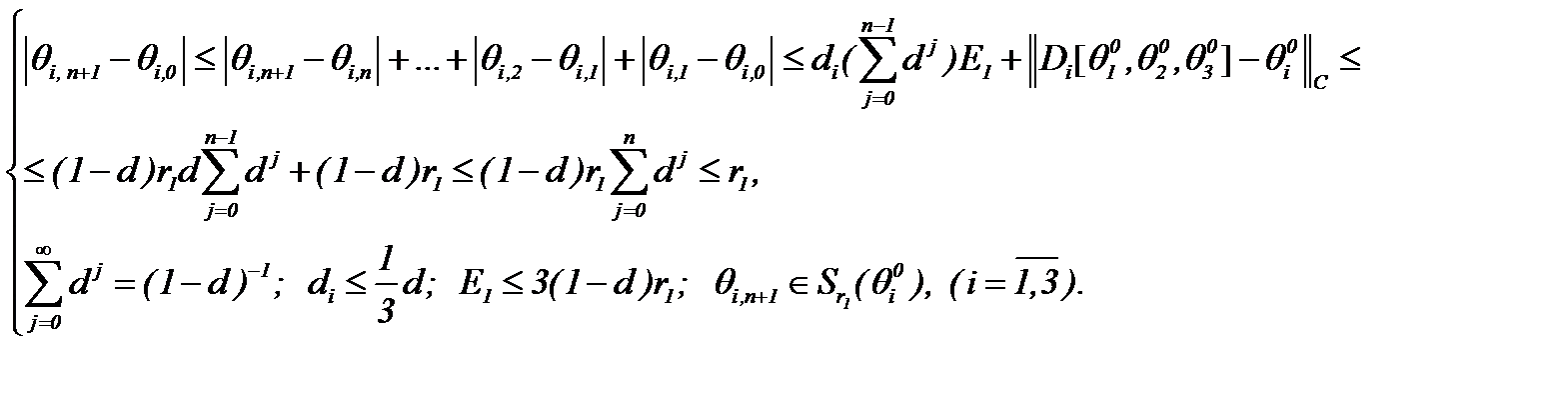
Значит, последовательности 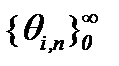 сходятся к пределу
сходятся к пределу 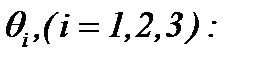
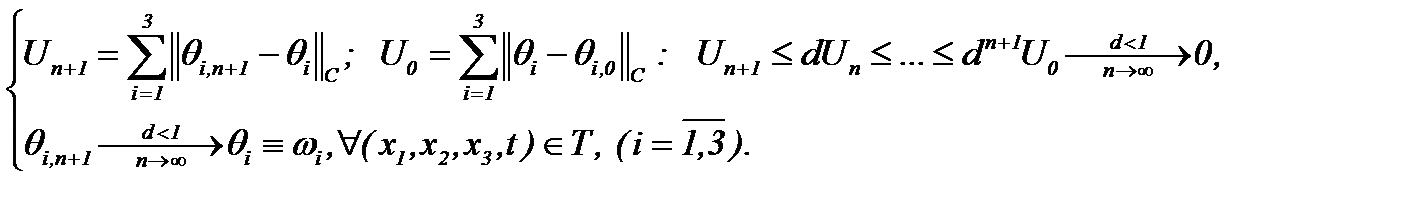 (3.12)
(3.12)
Поэтому, в соответствии с результатами теоремы 3, функции 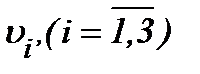 определяются из системы (3.5) следующим образом
определяются из системы (3.5) следующим образом
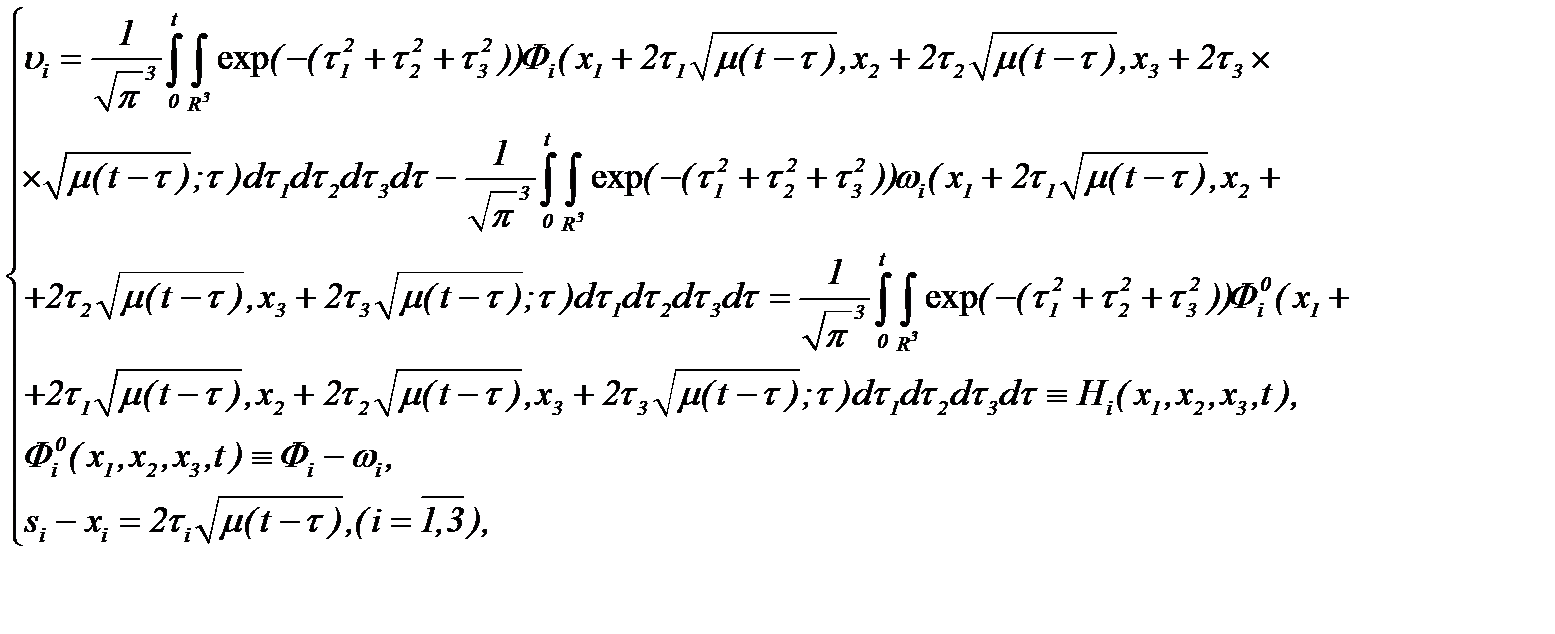 (3.5)*
(3.5)*
где 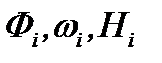 – известные функции и
– известные функции и
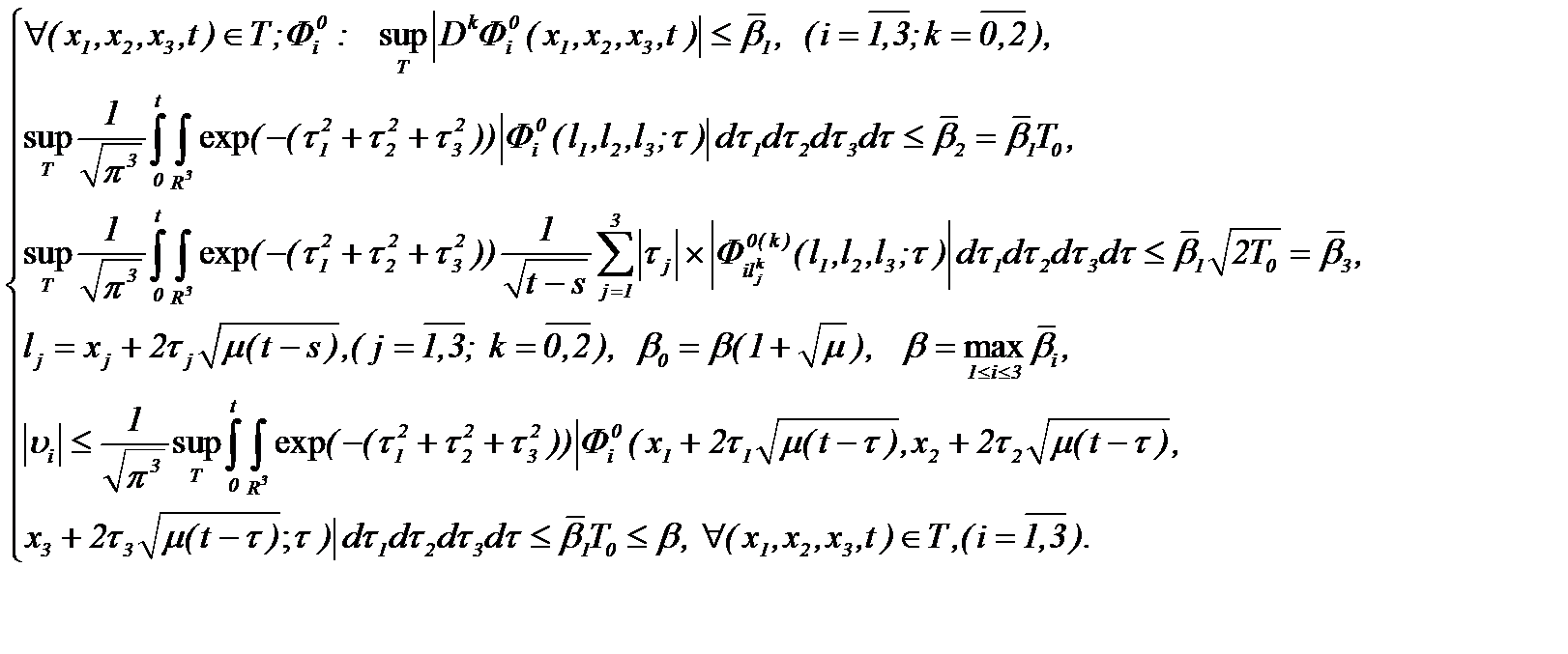 (3.13)
(3.13)
Откуда следует неравенство
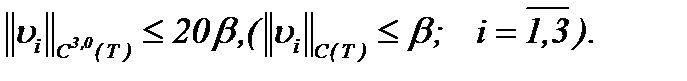
Тогда с учетом нормы пространства 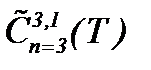 , получим
, получим
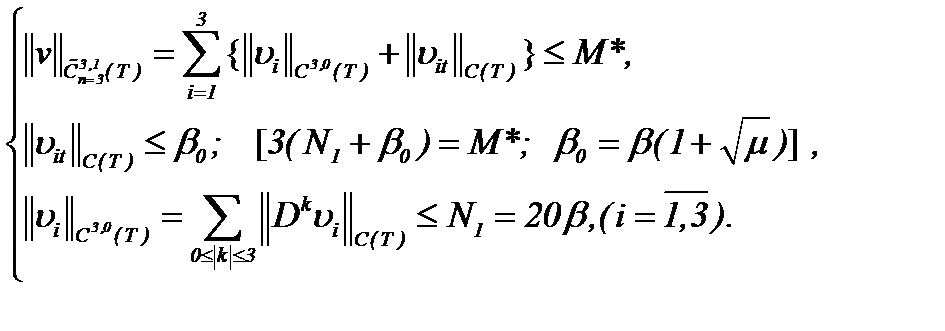 (3.14)
(3.14)
Значит, выражение (3.5)* удовлетворяет уравнению (3.4):
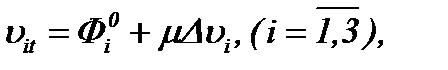 (3.4)*
(3.4)*
где
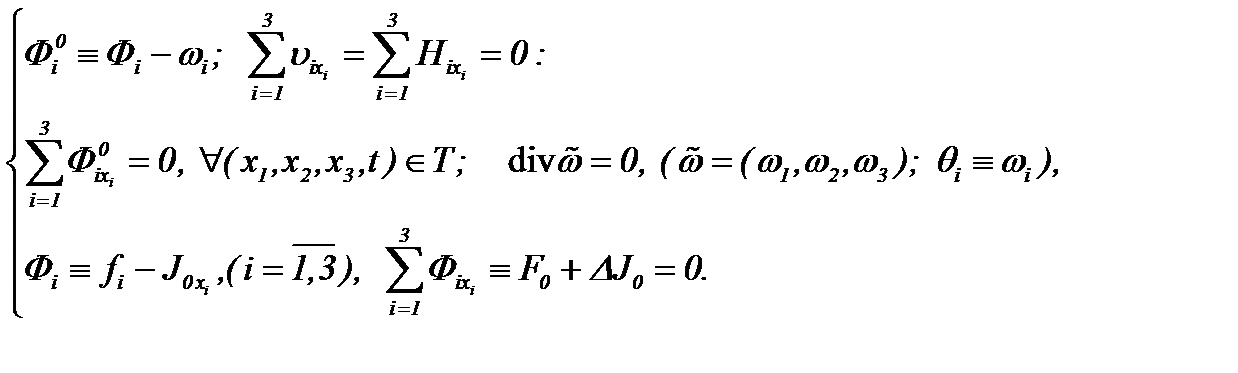
Действительно, рассчитав частные производные системы (3.5)*
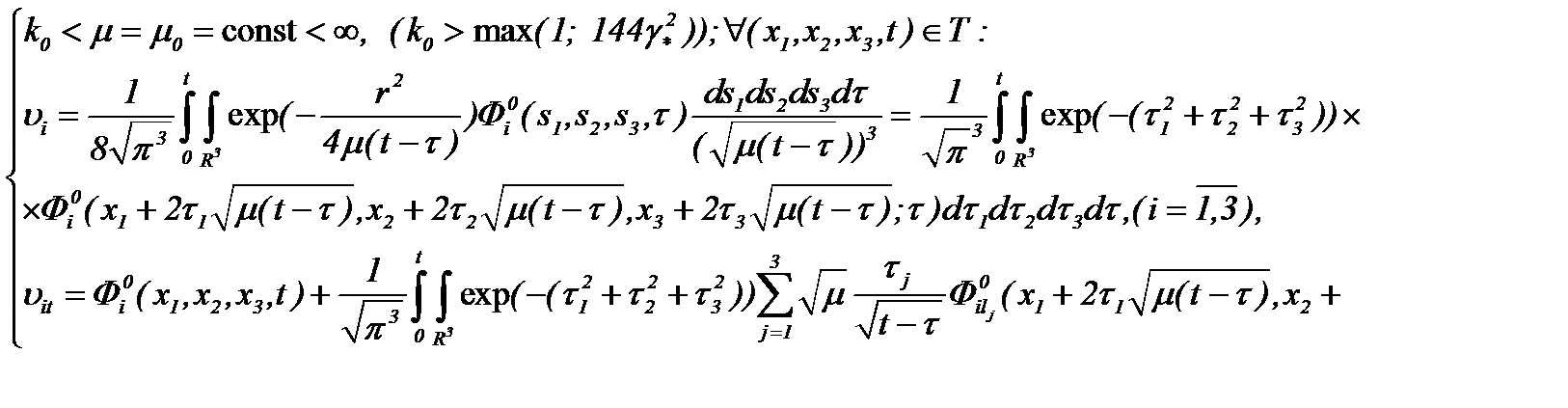
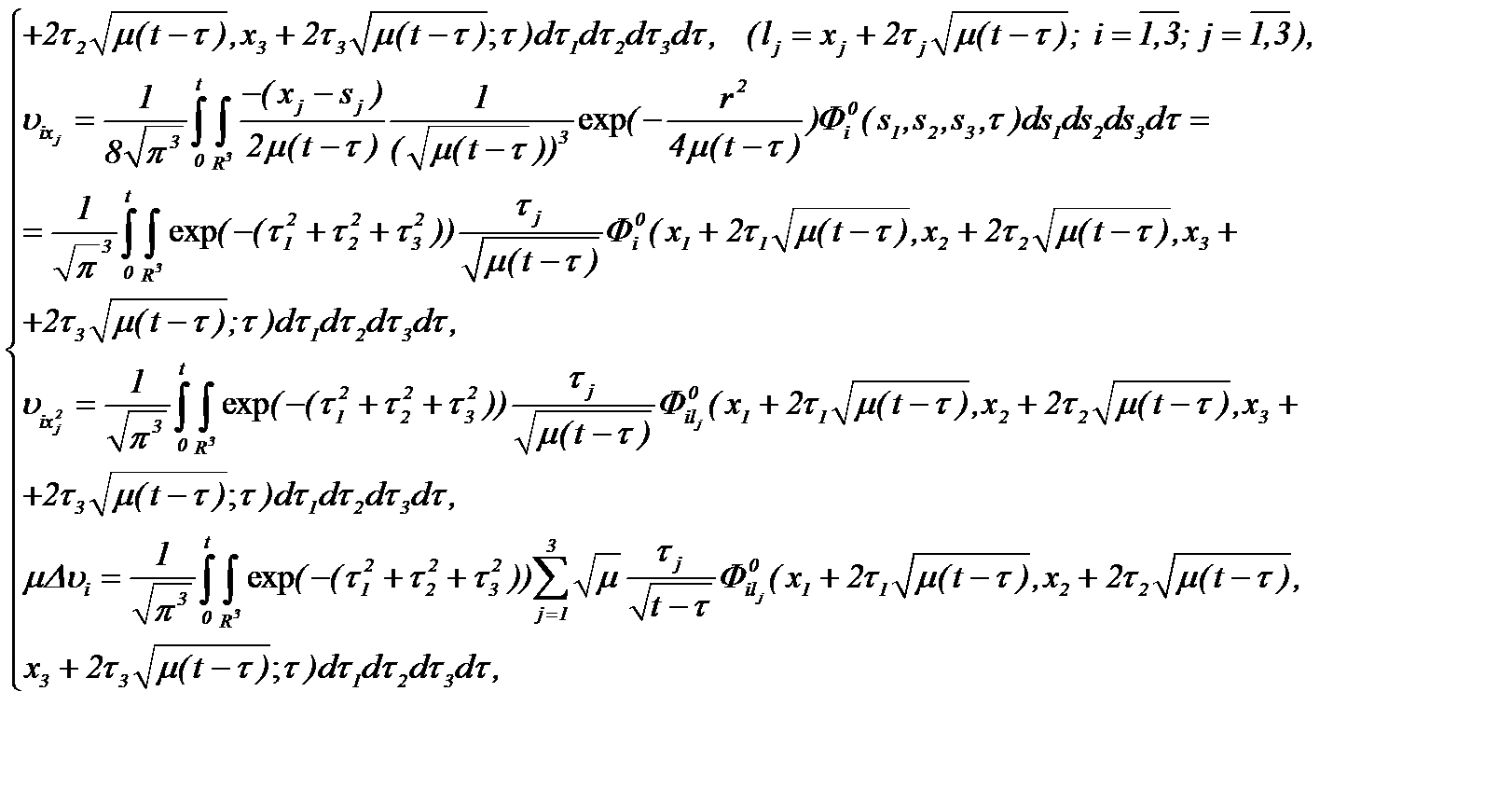 (3.15)
(3.15)
а, затем, подставляя (3.15) в (3.4)*, получим
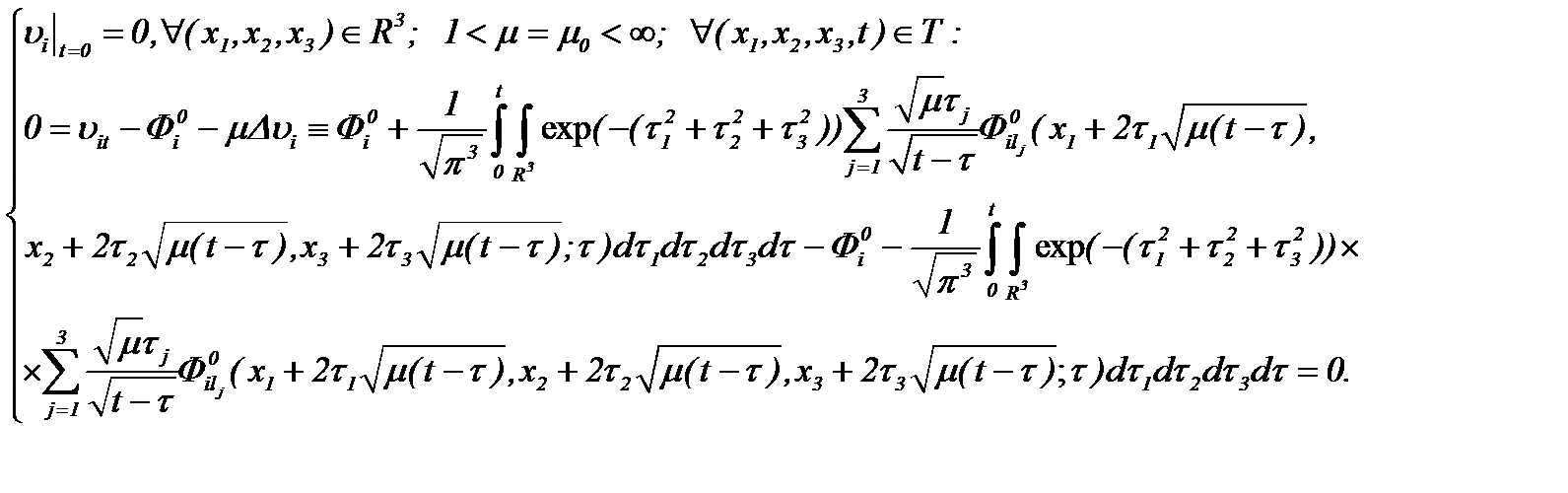 (3.16)
(3.16)
Что и требовалось показать.
На основе (3.3) из полученных результатов следует
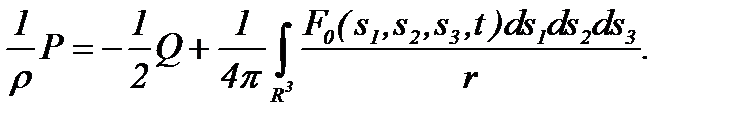 (3.17)
(3.17)
Поэтому, соответственно результатам теоремы 3, функции 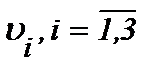 определяются из системы (3.5)* и удовлетворяют уравнению (1.2). Значит, для задачи Навье-Стокса (1.1) – (1.3)*, (A2) существует единственное гладкое решение в области
определяются из системы (3.5)* и удовлетворяют уравнению (1.2). Значит, для задачи Навье-Стокса (1.1) – (1.3)*, (A2) существует единственное гладкое решение в области 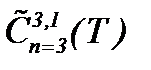 , а так как полученное решение (3.5)* непрерывно зависит от исходных данных
, а так как полученное решение (3.5)* непрерывно зависит от исходных данных 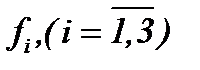 , то теорема 3 доказана. ■
, то теорема 3 доказана. ■
4. Жидкость с Весьма Малыми Значениями Вязкости с Условием (А3)
Теория дифференциальных уравнений в частных производных опирается на различные математические преобразования, которые упрощают исследованные проблемы так, что
становится возможным найти решение в некоторых пространствах [6, 13-15]. Для случая 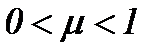 , соответствующего Re ≥ 2300, покажем, что применяемые нами преобразования приводят уравнения Навье-Стокса к линейному виду. Причем, полученная система имеет строгое аналитическое решение или решение, основанное на методе Пикара.
, соответствующего Re ≥ 2300, покажем, что применяемые нами преобразования приводят уравнения Навье-Стокса к линейному виду. Причем, полученная система имеет строгое аналитическое решение или решение, основанное на методе Пикара.
В последние десятилетия широко применяются методы с использованием интегральных преобразований. Обратное преобразование Фурье играет большую роль при решении краевых задач для уравнения Лапласа, некоторых интегральных уравнений, вычислении интегралов и т.д. Преобразование Лапласа развито для решения дифференциальных уравнений N -го порядка с постоянными коэффициентами и их систем, некоторых дифференциальных уравнений в частных производных, уравнений Вольтерра 1-го и 2-го рода с разностным ядром, интегральных уравнений с логарифмическим ядром и т.д. Однако, помимо частных случаев, эти преобразования не коснулись решения уравнений Навье-Стокса в общем виде.
Различные формулы интегральных преобразований получены при решении конкретных математических задач [13, 15], что предваряет их применение для решения других проблем, например, для исследования задач математической и теоретической физики, в том числе, уравнений Навье-Стокса. Тогда полученные в приведенных параграфах результаты дают все основания
полагать, что система Навье-Стокса (1.1) с условиями (1.2), (1.3) и (А3) может иметь гладкое и условно-гладкое единственное решение, причем в аналитической форме. Такое решение отвечает на поставленный Институтом Клея вопрос и дает возможность построить решение задачи Навье-Стокса (1.1) – (1.3), соответствующее вязкой несжимаемой жидкости.
4.1. Жидкость с вязкостью 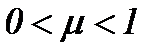 , когда
, когда 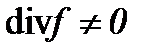
Пусть 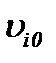 – начальные компоненты вектора скорости
– начальные компоненты вектора скорости 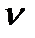 в момент времени
в момент времени 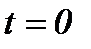 представлены в виде (1.3)
представлены в виде (1.3)
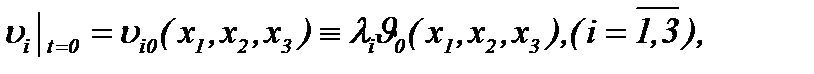 (4.1)
(4.1)
где 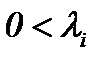 – известные константы. Тогда компоненты вектора скорости
– известные константы. Тогда компоненты вектора скорости  находим по правилу
находим по правилу
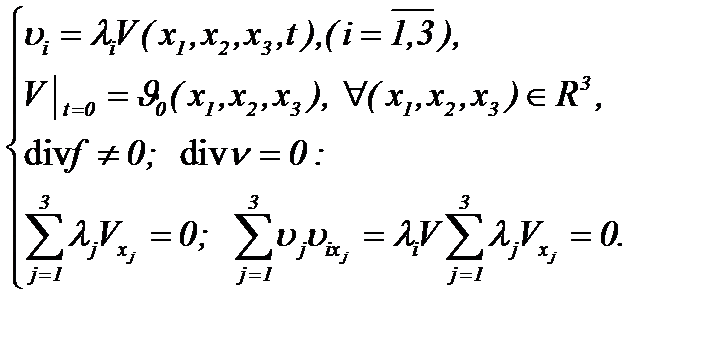 (4.2)
(4.2)
Следовательно, система (1.1) преобразуется к виду
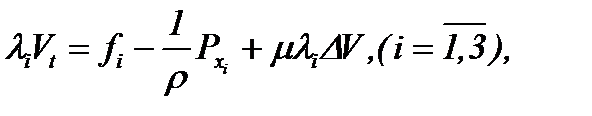 (4.3)
(4.3)
где 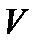 новая неизвестная функция, которая на основе (4.2) определяет решение задачи Навье-Стокса. Замена (4.2) эквивалентно преобразует систему (1.1) к линейным неоднородным уравнениям (4.3). Причем, в статье [8] задача (4.1) – (4.3) исследована как в
новая неизвестная функция, которая на основе (4.2) определяет решение задачи Навье-Стокса. Замена (4.2) эквивалентно преобразует систему (1.1) к линейным неоднородным уравнениям (4.3). Причем, в статье [8] задача (4.1) – (4.3) исследована как в 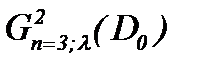 , так и в
, так и в 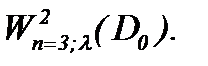
Здесь задача (4.1) – (4.3) исследуется в пространстве 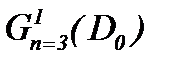 , для чего, в первую очередь, требуется найти давление
, для чего, в первую очередь, требуется найти давление 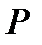 . Из системы (4.3), применяя алгоритм АПС, т.е. считаем, что первое уравнение (4.3), когда i = 1, дифференцируемо по
. Из системы (4.3), применяя алгоритм АПС, т.е. считаем, что первое уравнение (4.3), когда i = 1, дифференцируемо по 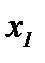 , второе уравнение (4.3), когда i = 2, – по
, второе уравнение (4.3), когда i = 2, – по 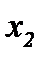 , третье (4.3), когда i = 3, – по
, третье (4.3), когда i = 3, – по 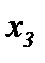 , а, затем, суммируя, получим
, а, затем, суммируя, получим
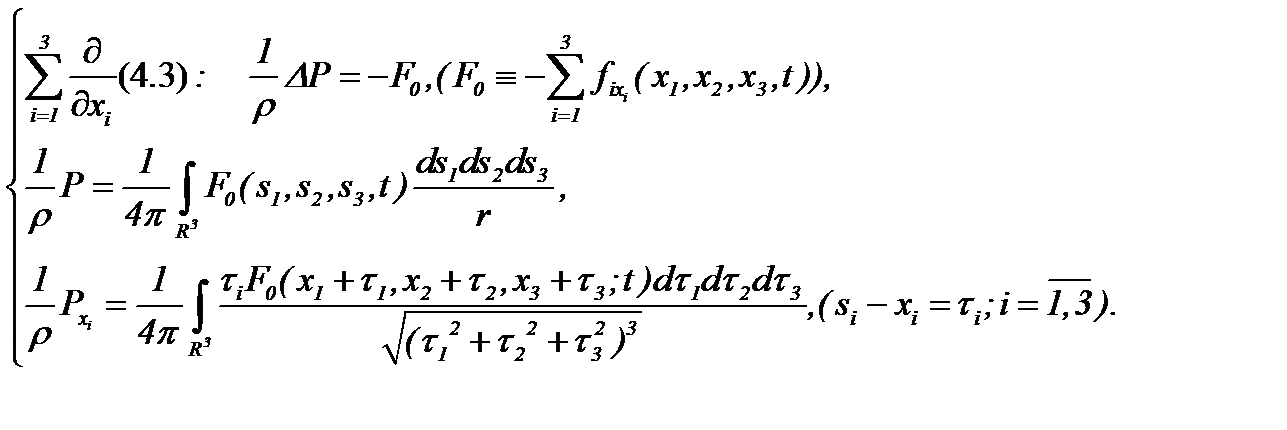 (4.4)
(4.4)
Поэтому, подставляя (4.4) в (4.3), имеем
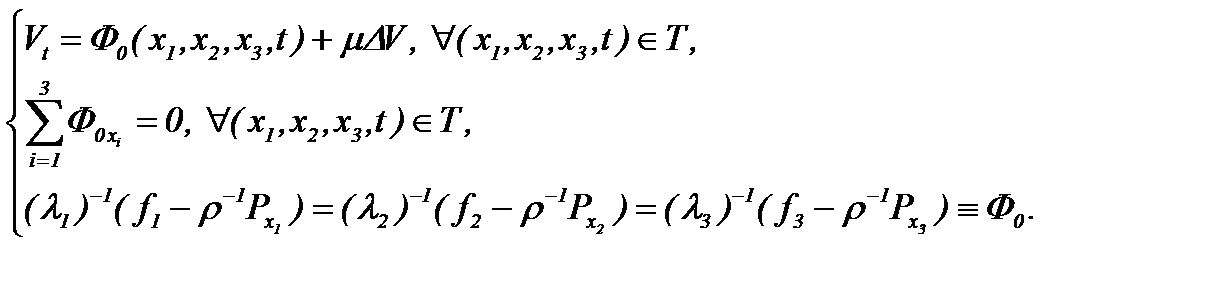 (4.5)
(4.5)
Следовательно, система (4.3) трансформируется в линейные уравнения теплопроводности с
условием Коши вида (4.5), а, значит, разрешима в классе ограниченных функций с достаточно гладкими начальными данными [13, 14], а потому дает строго единственное решение задачи Навье-Стокса в 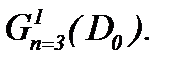 В самом деле, из уравнения (4.5) следует, что
В самом деле, из уравнения (4.5) следует, что
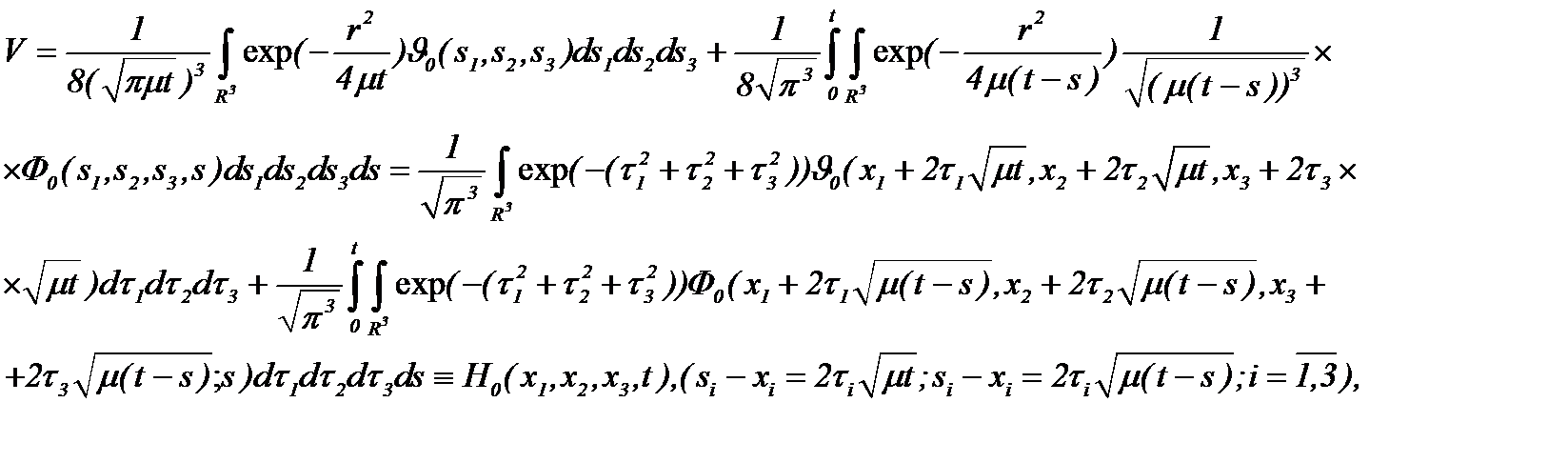 (4.6)
(4.6)
где 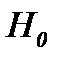 – известная функция, причем найденное решение (4.6) удовлетворяет уравнению (4.5).
– известная функция, причем найденное решение (4.6) удовлетворяет уравнению (4.5).
Вычислив частные производные уравнения (4.6)
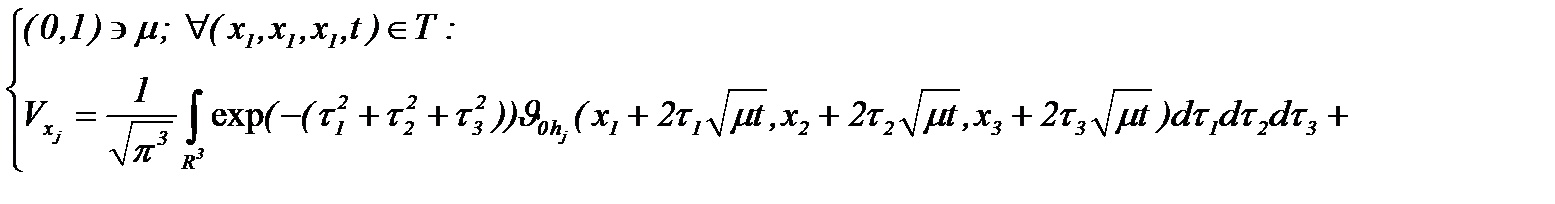
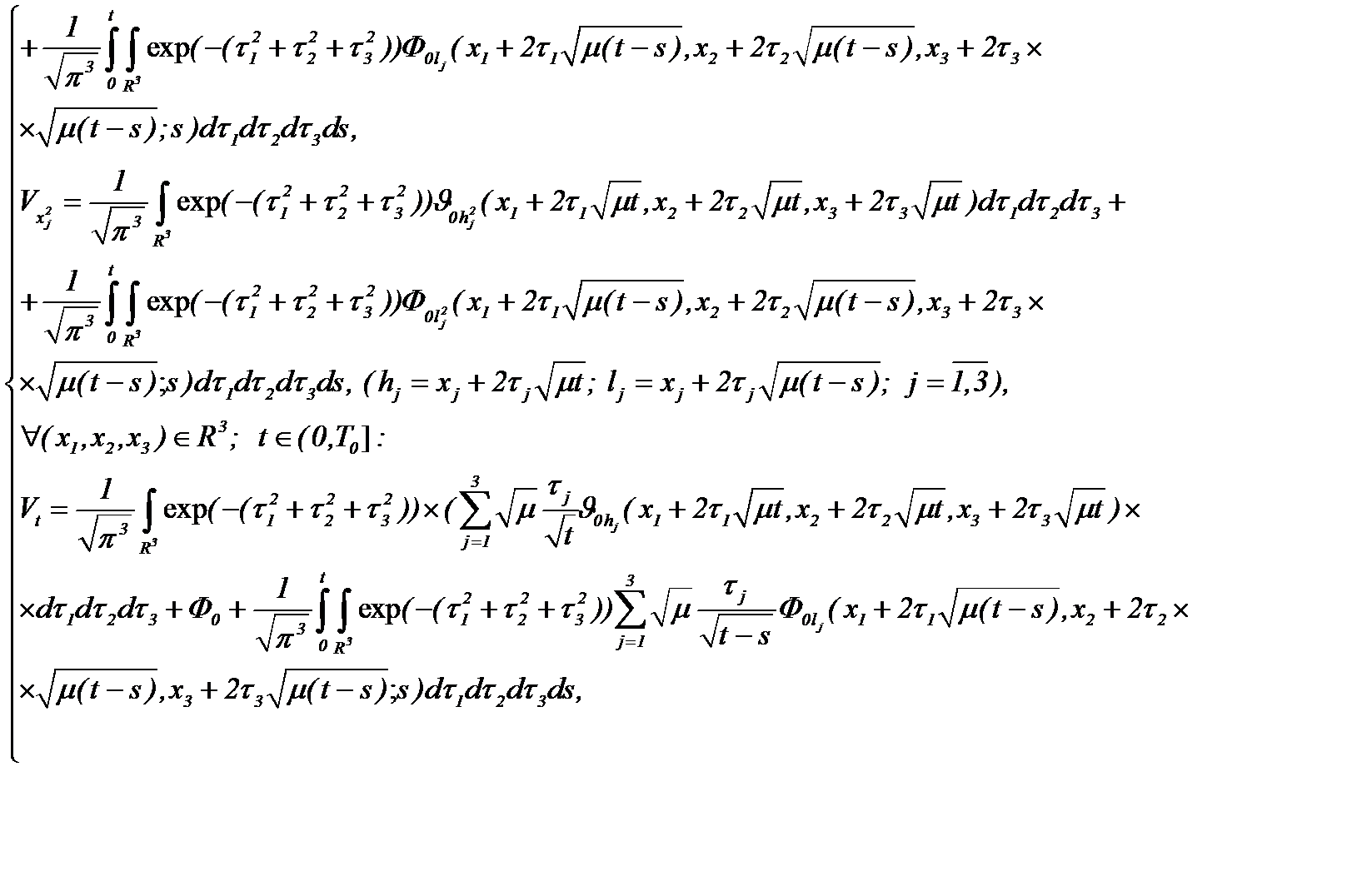 (4.7)
(4.7)
а, затем, подставляя (4.7) в (4.5), имеем
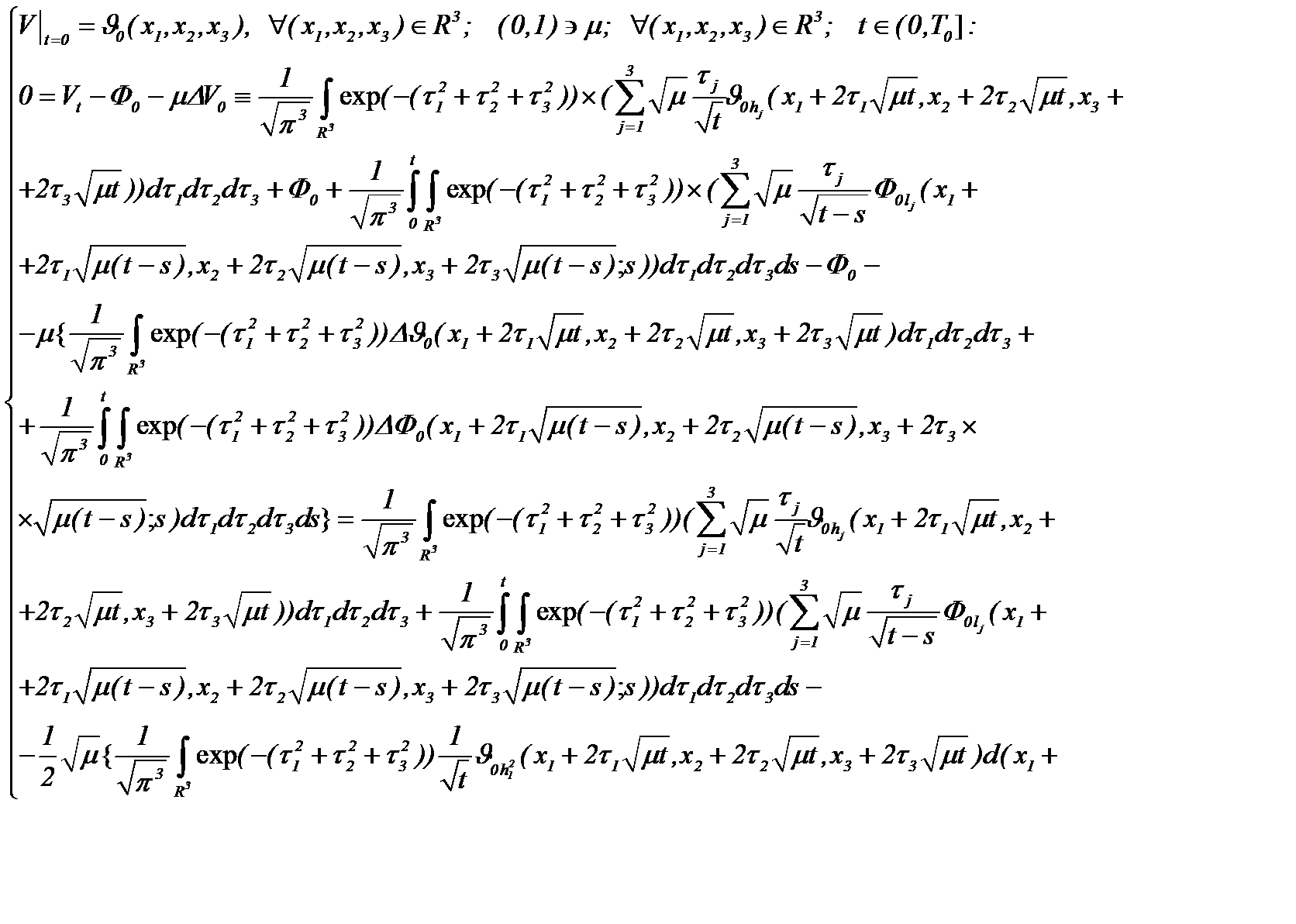

т.е. то, что система (4.6) удовлетворяет задачу (4.5), что и требовалось доказать.
Доказательство ограниченности решений (4.6) проведем в 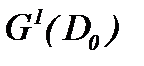 , поскольку справедливо
, поскольку справедливо
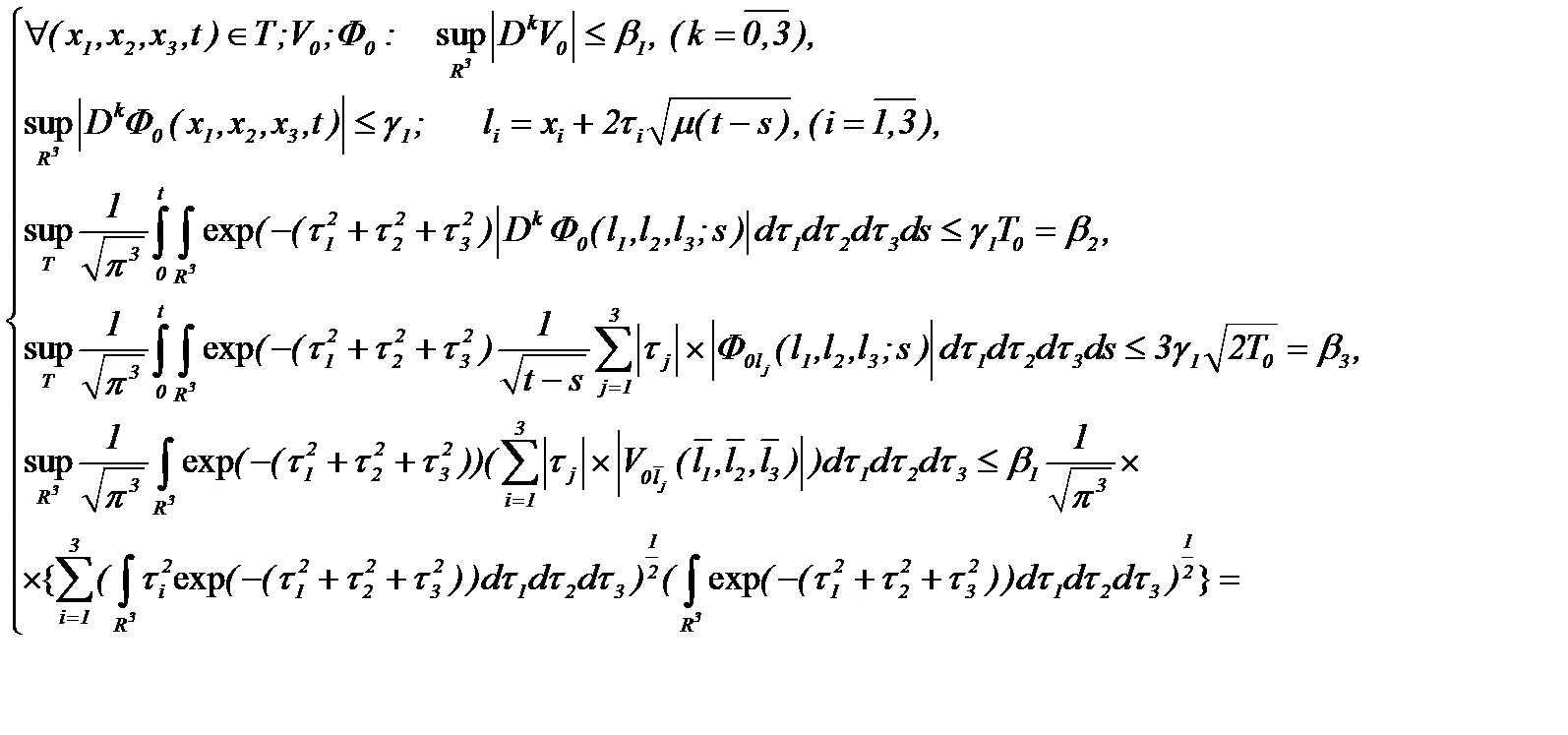
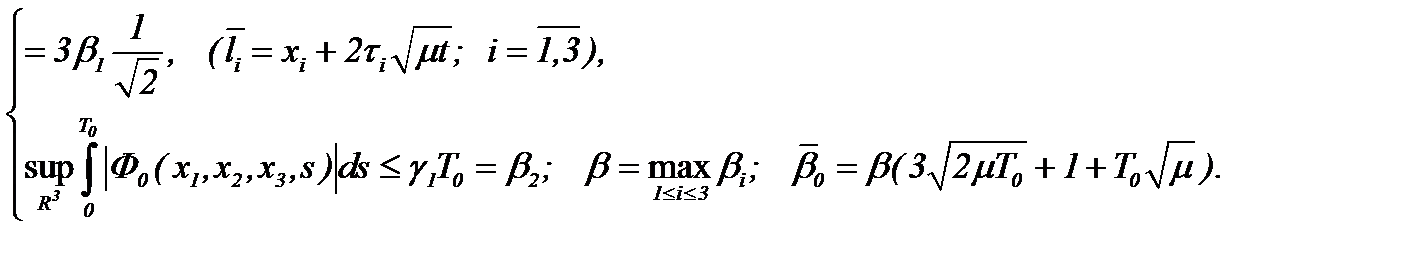 (4.8)
(4.8)
Действительно, учитывая (4.8) и оценивая (4.6) в смысле нормы  , имеем
, имеем
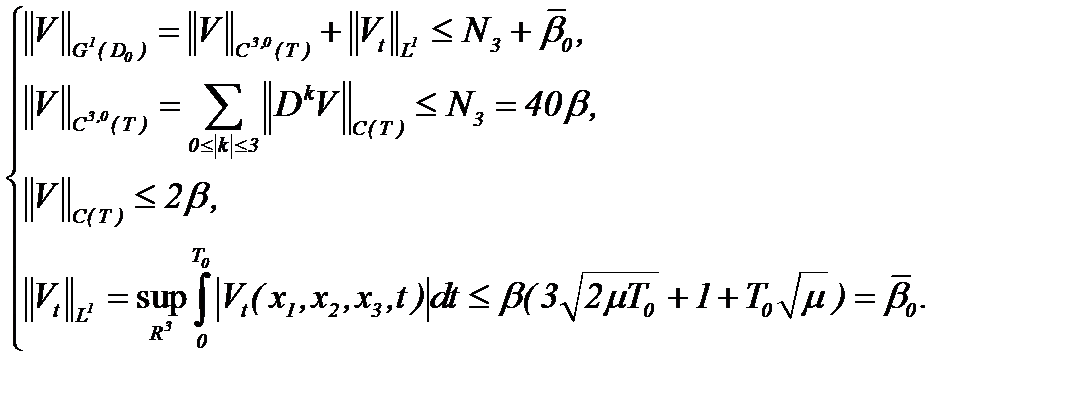
Единственность решения  уравнения (4.6) в
уравнения (4.6) в 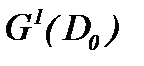 очевидна из метода от противного. В самом деле, предполагая
очевидна из метода от противного. В самом деле, предполагая 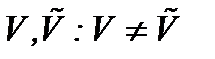 и допуская, что эти решения удовлетворяют уравнению (4.6) с условием (4.2), получим противоречие
и допуская, что эти решения удовлетворяют уравнению (4.6) с условием (4.2), получим противоречие 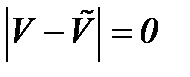 . Значит, уравнение (4.6) имеет единственное решение.
. Значит, уравнение (4.6) имеет единственное решение.
Уравнение (4.6) с условием (4.2), (4.8) имеет место, когда гладкость функций требуется только по 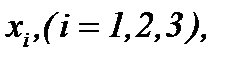 так как производная первого порядка во времени определяется для всех
так как производная первого порядка во времени определяется для всех 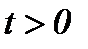 . Поэтому на основе преобразования (4.2) получаем решение системы (1.1), которое удовлетворяет условию (1.2), т.е.
. Поэтому на основе преобразования (4.2) получаем решение системы (1.1), которое удовлетворяет условию (1.2), т.е.
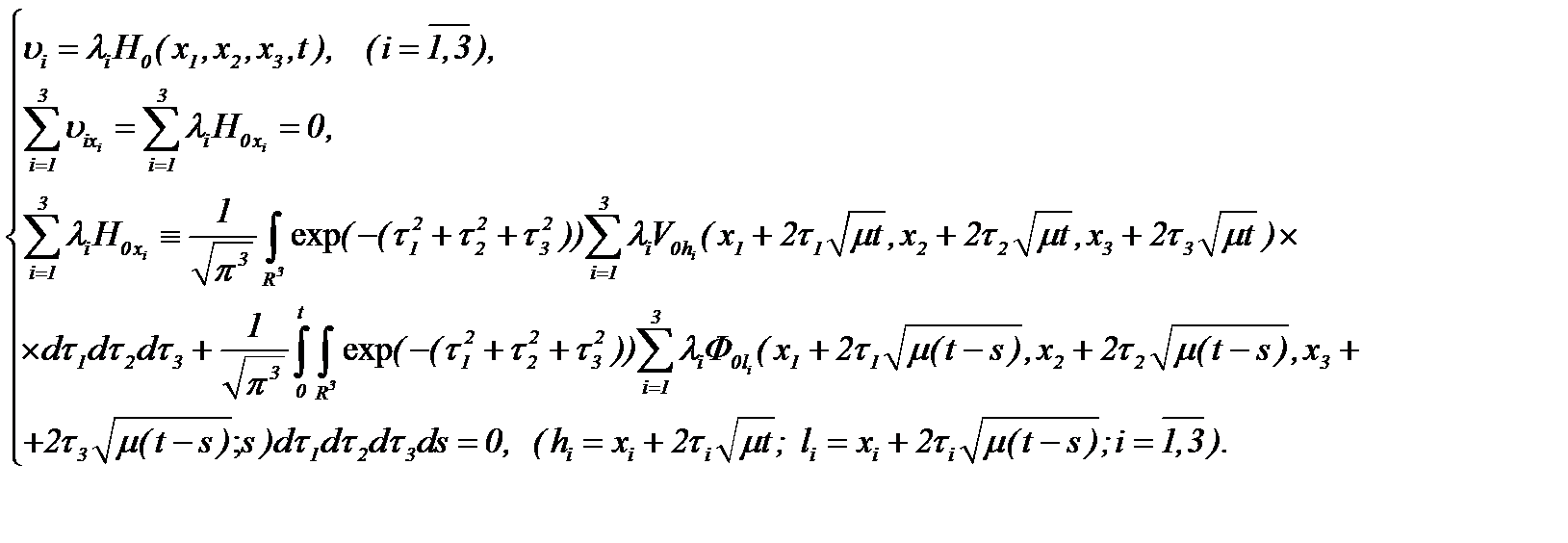 (4.9)
(4.9)
Для системы (4.9) в смысле нормы 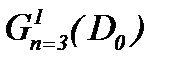 имеем соответствующую оценку и теорему
имеем соответствующую оценку и теорему
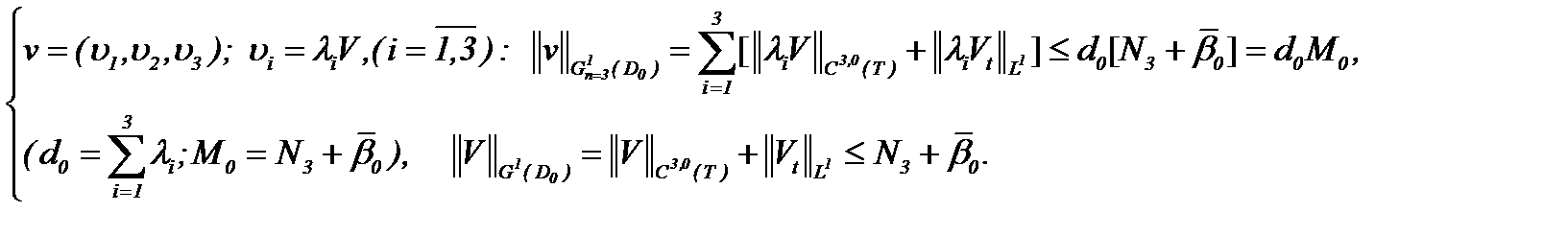 (4.10)
(4.10)
Теорема 4. Задача (1.1), (1.2), (4.1) с условиями (4.2), (4.8) и (4.10) имеет единственное решение в 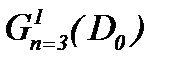 , которое определяется по правилу (4.9).
, которое определяется по правилу (4.9).
|
|
|
История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...
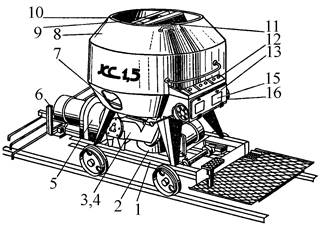
Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
© cyberpedia.su 2017-2025 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!