

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы...
Интересное:
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
5.3. Жидкость со средней и большой вязкостью, когда 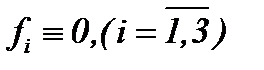
В 5.1 и 5.2 изучена жидкость со средней вязкостью, если 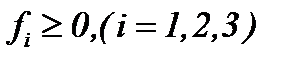 . Здесь рассмотрим метод интегрирования уравнений Навье-Стокса (1.1) со средним и небольшим числом Рейнольдса (
. Здесь рассмотрим метод интегрирования уравнений Навье-Стокса (1.1) со средним и небольшим числом Рейнольдса ( 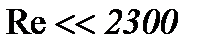 ) для уравнений [12], содержащих все инерционные
) для уравнений [12], содержащих все инерционные
члены и условие  . Цель этого пункта: найти для метода (5.22) такую модификацию, чтобы получить аналитическое решение задачи Коши для однородных уравнений Навье-Стокса в
. Цель этого пункта: найти для метода (5.22) такую модификацию, чтобы получить аналитическое решение задачи Коши для однородных уравнений Навье-Стокса в 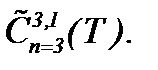
В этой связи, здесь исследуем задачу
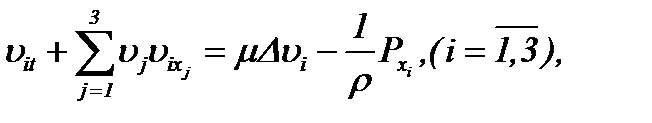 (5.31)
(5.31)
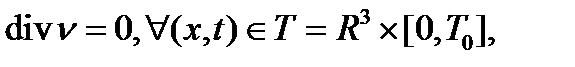 (5.32)
(5.32)
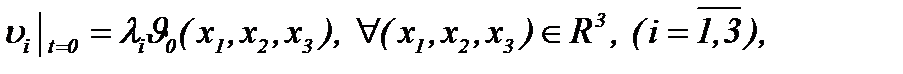 (5.33)
(5.33)
где 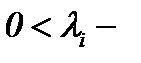 известные константы и
известные константы и
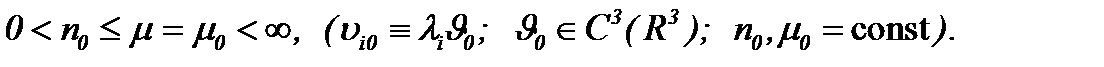 (5.34)
(5.34)
Чтобы достичь поставленной цели, будем считать, что существуют функции 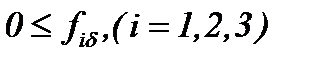 , которые удовлетворяют условиям
, которые удовлетворяют условиям
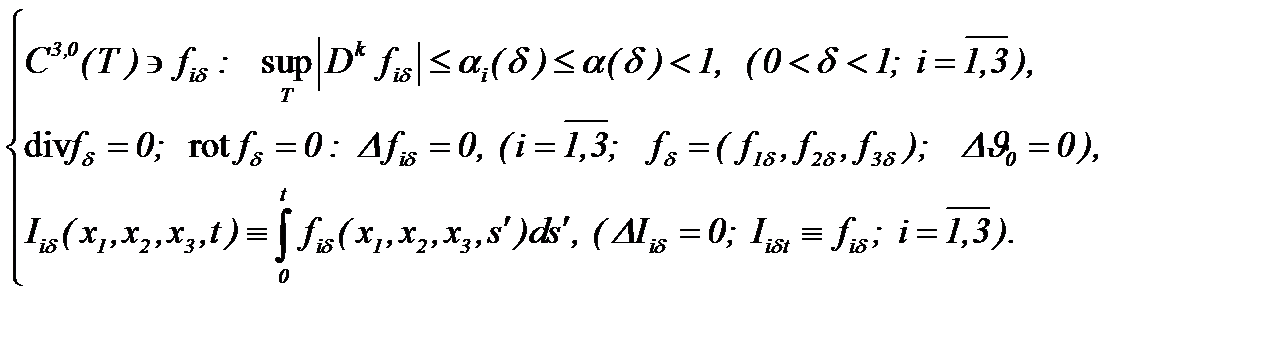 (5.35)
(5.35)
Тогда применим метод
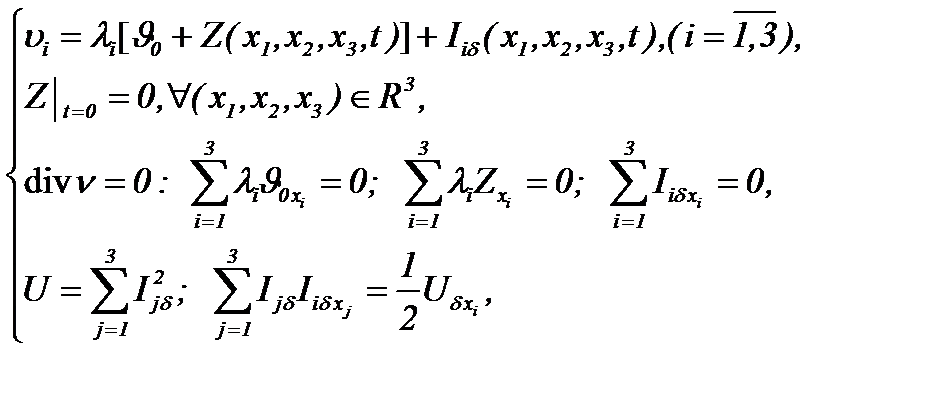 (5.36)
(5.36)
для которого соблюдаются условия
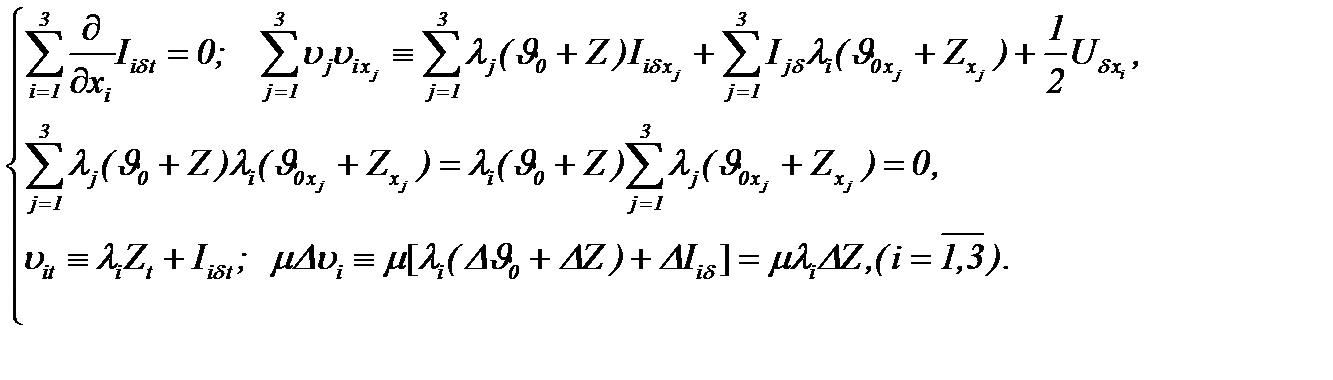 (5.37)
(5.37)
С помощью преобразования (5.36) при выполнении условий (5.32) – (5.35) и (5.37), так как все инерционные члены линеаризуется на основе функций 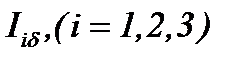 , уравнение
, уравнение
Навье-Стокса с трением (5.31) сводится к неоднородным линейным уравнениям
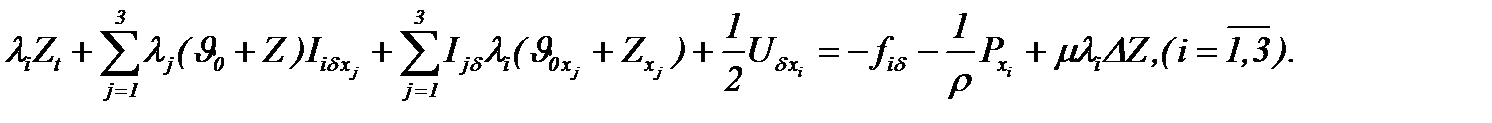 (5.38)
(5.38)
Из системы (5.38) с учетом условий (5.31) – (5.33), применяя алгоритм АПС, получим уравнение:
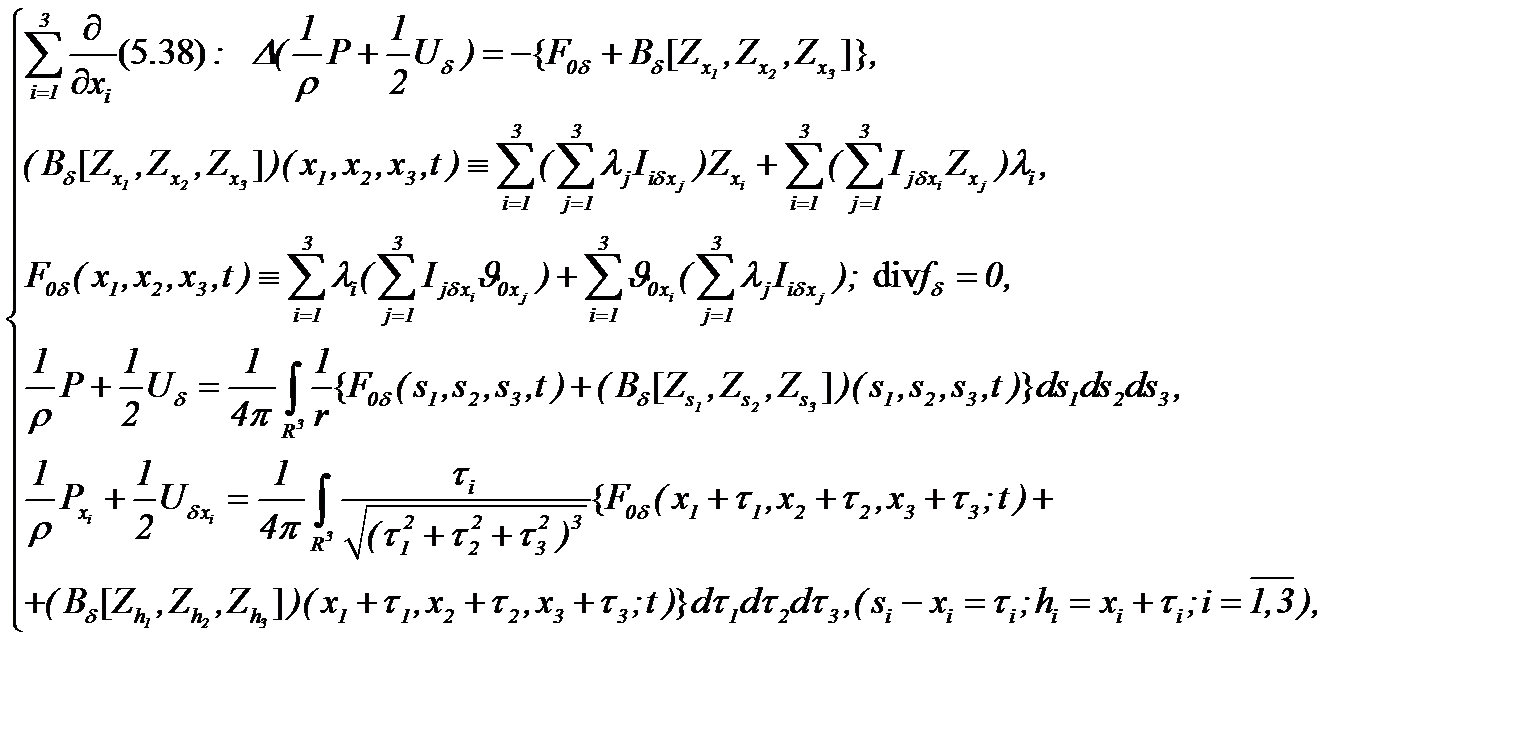 (5.39)
(5.39)
так как имеет место
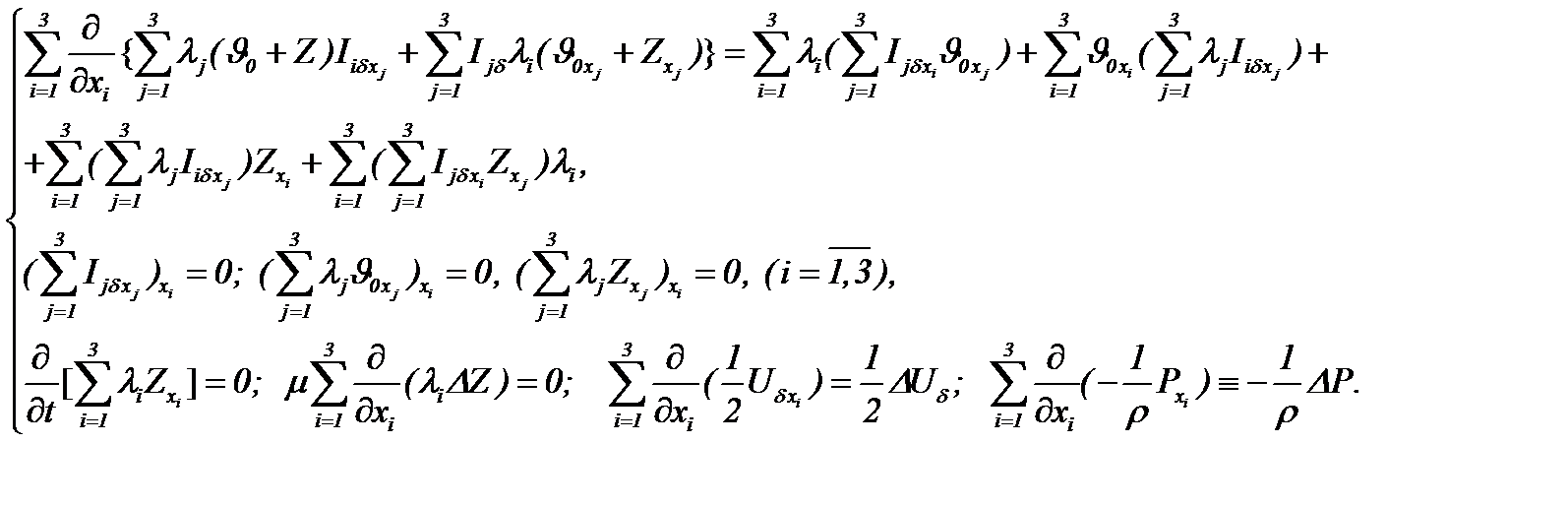
Тогда на основании (5.39) система (5.38) эквивалентно преобразуется к виду
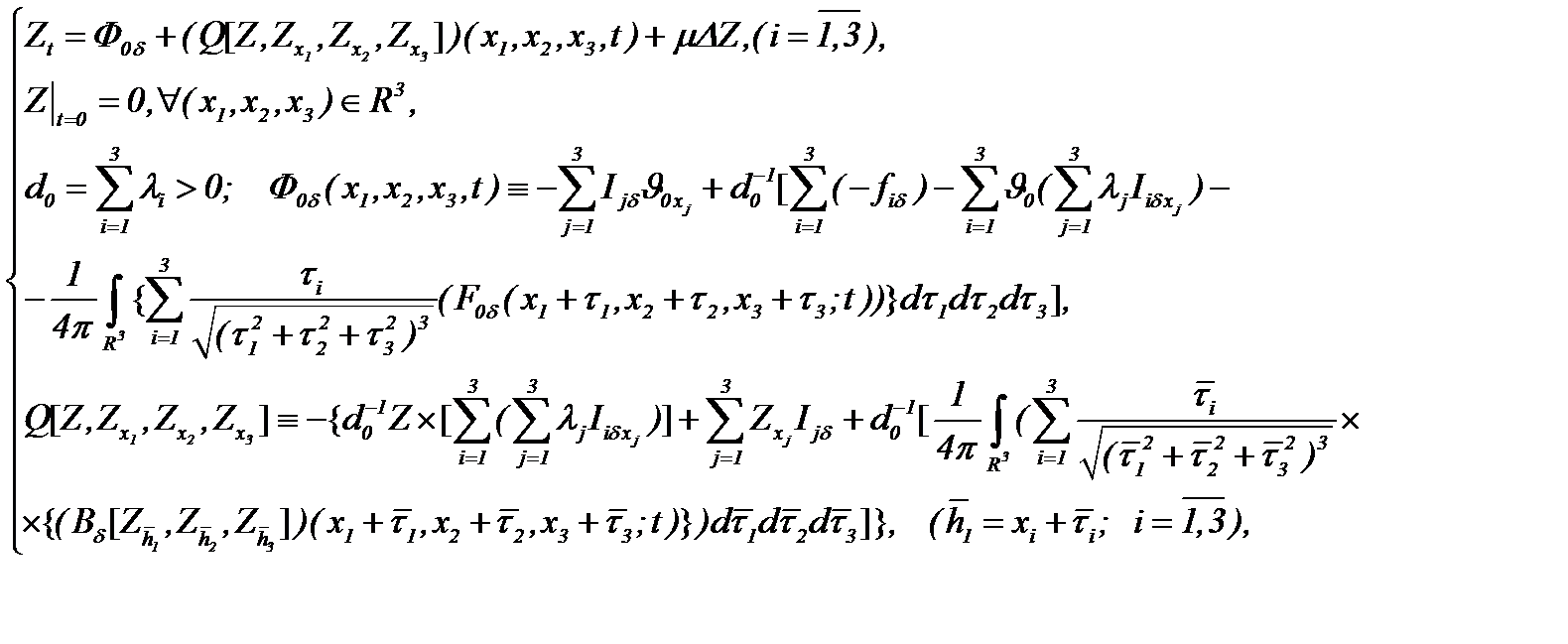 (5.40)
(5.40)
для которого имеем
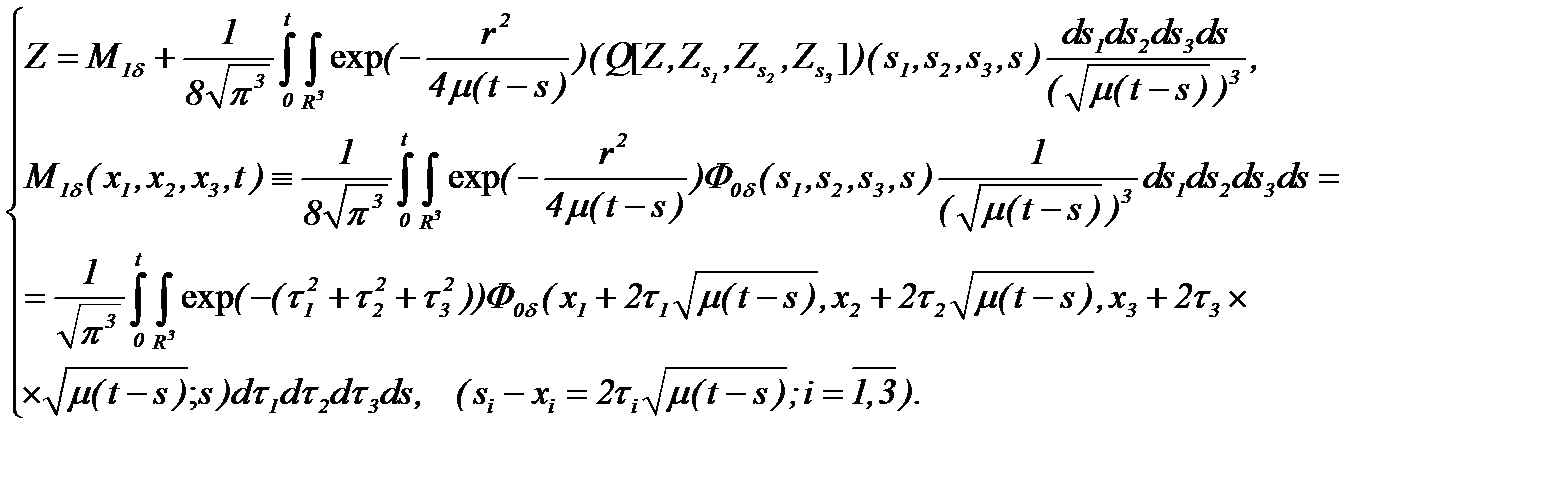 (5.41)
(5.41)
Чтобы доопределить (5.41), вычислим частные производные по 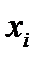 и на основе математических преобразований выведем систему интегральных уравнений
и на основе математических преобразований выведем систему интегральных уравнений
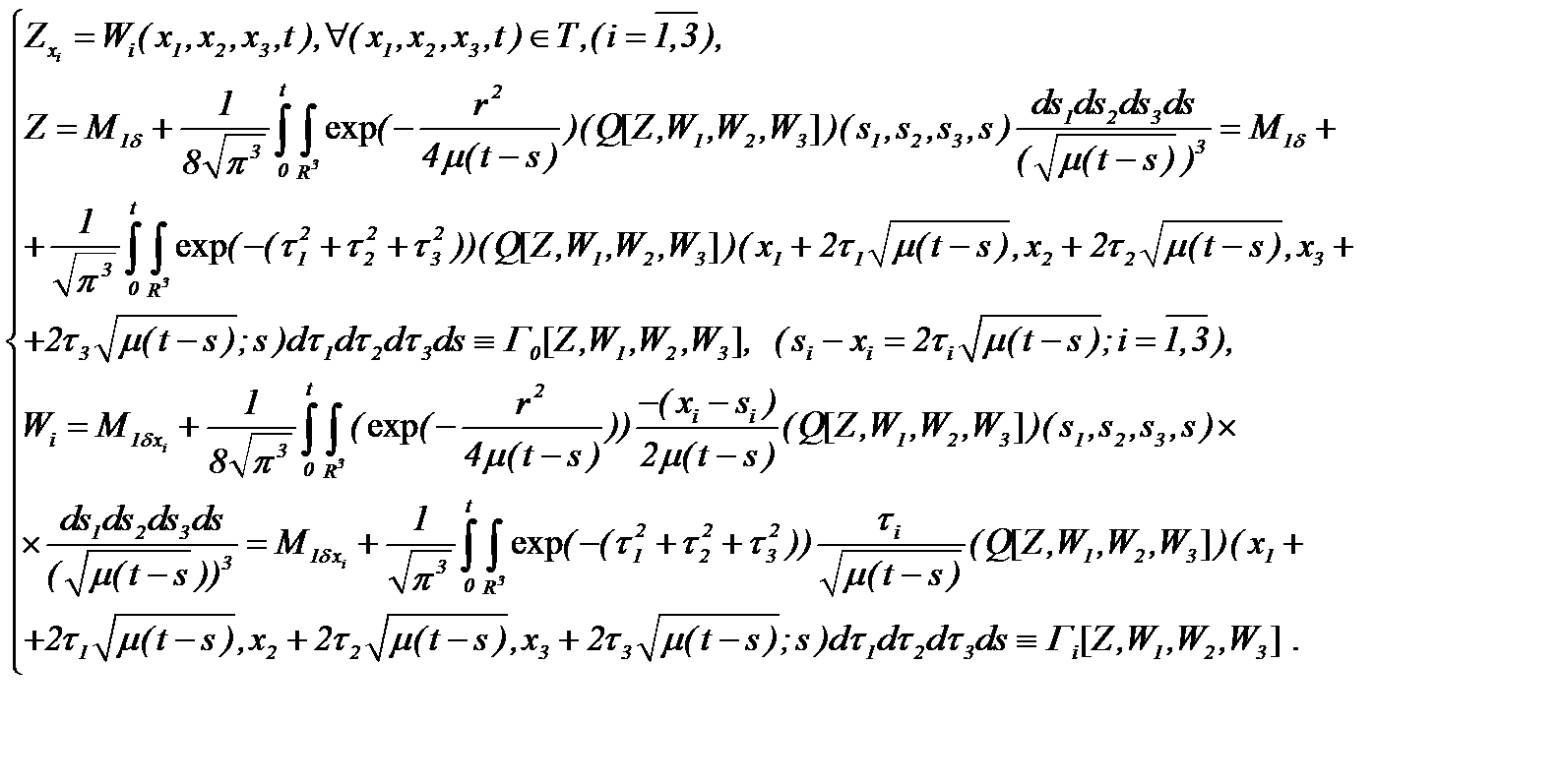 (5.42)
(5.42)
Таким образом, для решения задачи (5.40) получили систему (5.42) из четырех интегральных уравнений с четырьмя неизвестными функциями.
Пусть для известных функций 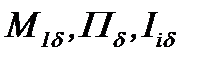 имеет место
имеет место
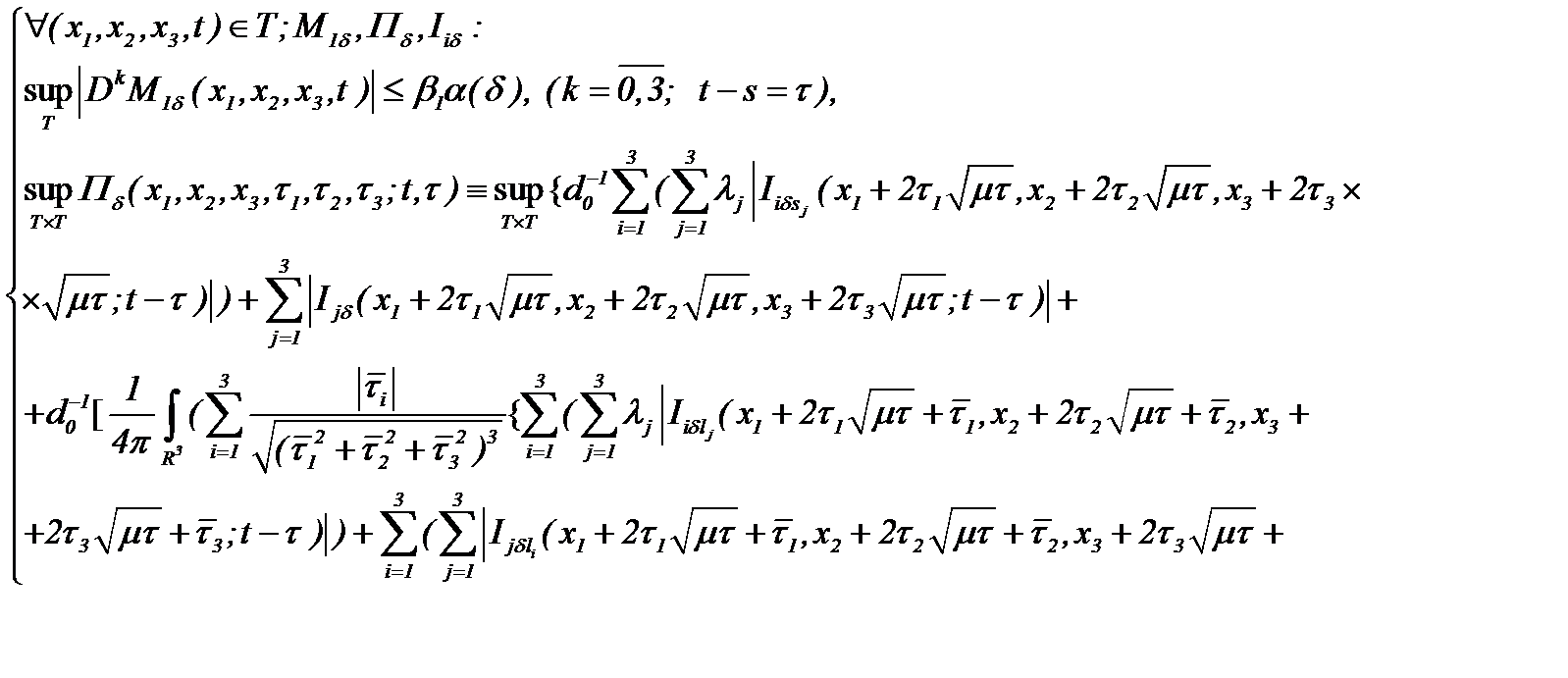
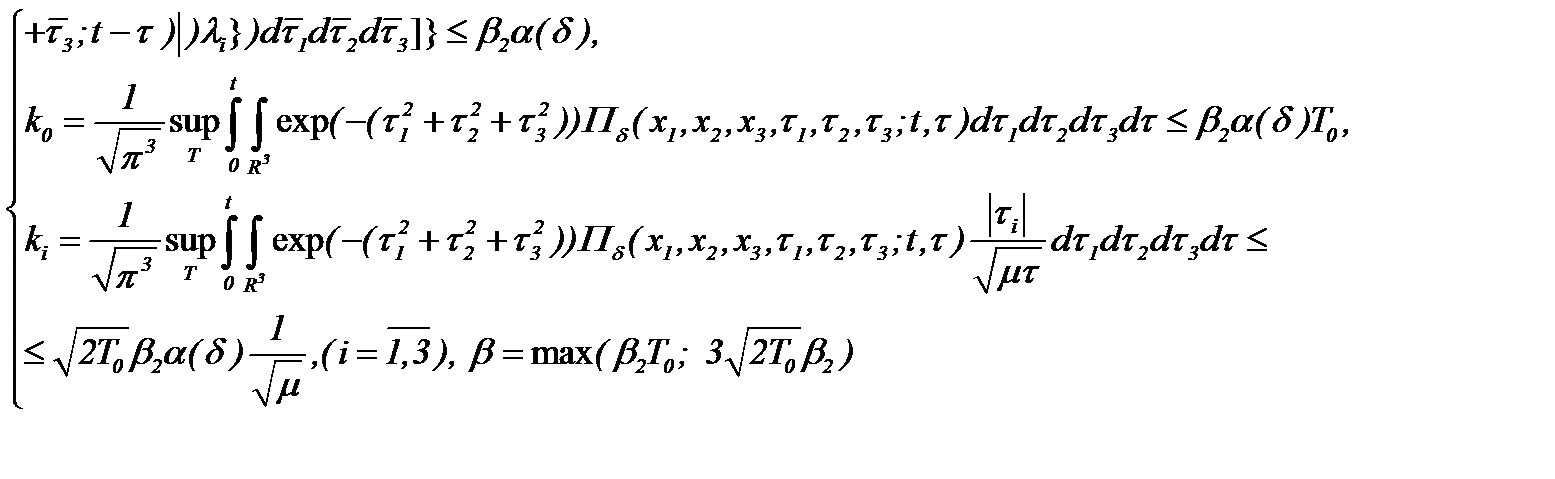 (5.43)
(5.43)
и
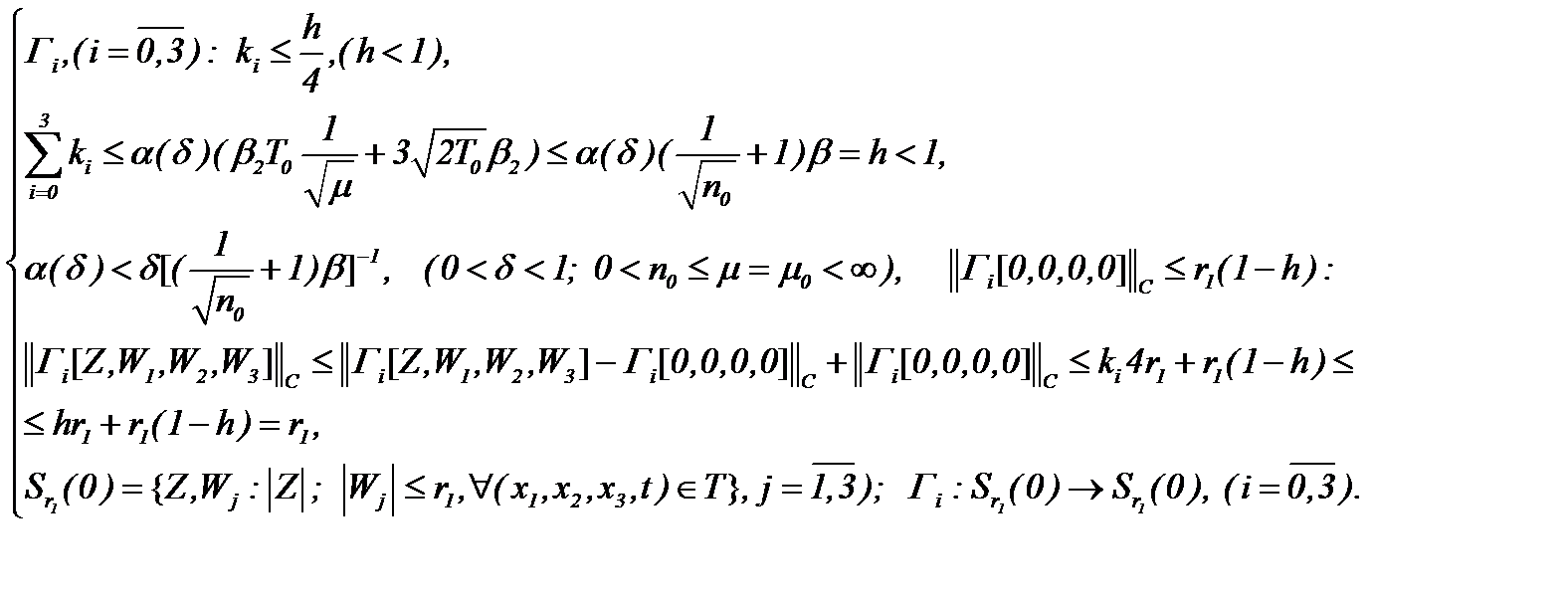 (5.44)
(5.44)
Тогда относительно операторов 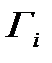 выполняется принцип сжимающих отображений. Поэтому, система (5.42) разрешима, решение которой строим на основе метода Пикара, а именно
выполняется принцип сжимающих отображений. Поэтому, система (5.42) разрешима, решение которой строим на основе метода Пикара, а именно
 (5.45)
(5.45)
Учитывая выводы метода Пикара, имеем
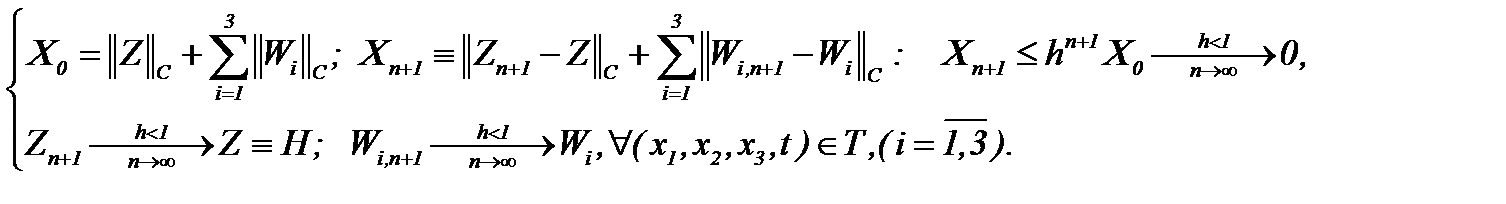 (5.46)
(5.46)
Значит, на основании результатов (5.13) – (5.15) получим, что последовательности функций 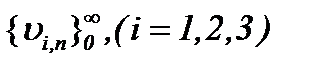 , построенные по правилу
, построенные по правилу
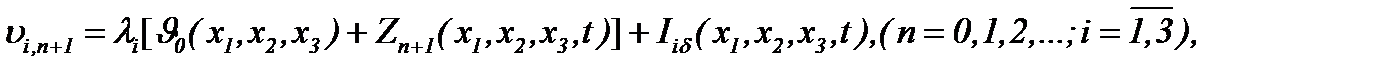 (5.47)
(5.47)
сходятся к пределу 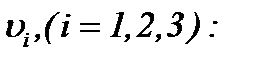
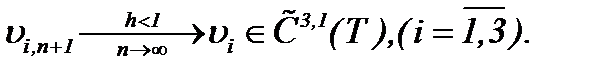 (5.48)
(5.48)
Очевидно, малые изменения 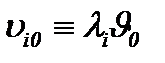 или
или 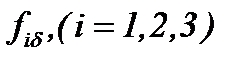 не способны влиять на решение
не способны влиять на решение
(5.36), значит, решение непрерывно зависит от этих данных. Поэтому корректная постановка задачи (5.31) – (5.33) в 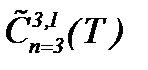 следует из результатов теоремы 6*.
следует из результатов теоремы 6*.
Отметим, что если же 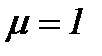 , причем (см. (5.44)):
, причем (см. (5.44)):

то, очевидно, задача Навье-Стокса (5.31) – (5.33) разрешима в 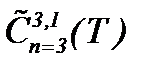 .
.
|
|
|

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...
© cyberpedia.su 2017-2026 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!